Модели типа 1.1—1.5 с вероятностным распределением спроса и времени выполнения заказа

2. Модели типа 1.1—1.5 с вероятностным распределением спроса и времени выполнения заказа

Вместо предпосылки о постоянстве и детерминированности спроса на товар используется более реалистичный подход о предполагаемой известности распределения темпа спроса и времени выполнения заказа.

Рассмотрим подробнее модели с фиксированным размером заказа. Модели с вероятностным распределением спроса и времени выполнения заказа рассмотрены в следующем разделе, где они решаются на основе имитационного подхода.

Модель 1.1 наиболее экономичного размера заказа. Заказ, пополняющий запасы, поступает как одна партия. Уровень запасов убывает с постоянной интенсивностью пока не достигает нуля. В этой точке поступает заказ, размер которого равен Q, и уровень запасов восстанавливается до максимального значения. При этом оптимальным решением задачи будет тот размер заказа, при котором минимизируются общие издержки за период (рис. 11.1).

Пусть Q — размер заказа; Т — протяженность периода планирования; D — величина спроса за период планирования; d — величина спроса в единицу времени; К — издержки заказа; Н — удельные издержки хранения за период; h — удельные издержки хранения в единицу времени.

Тогда:

(D/Q)K — совокупные издержки заказа;

Модель 1.3 оптимального размера заказа в предположении, что допускается дефицит продукта и связанная с ним упущенная прибыль (рис. 11.3).

Пусть р — упущенная прибыль в единицу времени, возникающая в результате дефицита одной единицы продукта;

Р — упущенная прибыль за период, возникающая в результате дефицита одной единицы продукта. Тогда:

Q* =( 2dK/h)^l/2 х ((Р+hVp)^1/2=

=( 2DK/H)^1/2 х ((Р+Н)/P)^1/2 — оптимальный размер заказа;

S* =( 2dK/h)^1/2 x (p/(h+p))^1/2 =

=(2DK/H)^1/2 х (Р/(H+Р))^1/2 — максимальный размер запаса;

R = Q*— S* — максимальный дефицит.

Модель 1.4 производства и распределения. В предыдущей модели мы допускали, что пополнение запаса происходит единовременно. Но в некоторых случаях, особенно в промышленном производстве, для комплектования партии товаров требуется значительное время и производство товаров для пополнения запасов происходит одновременно с удовлетворением спроса. Такой случай показан на рис. 11.4.

Спрос и производство являются частью цикла восстановления запасов. Пусть u — уровень производства в единицу времени, К — фиксированные издержки производства.

Тогда:

совокупные издержки хранения = (средний уровень запасов) х Н = Q/2[l-d/u] Н;

средний уровень запасов = (максимальный уровень запасов)/2;

максимальный уровень запасов = u t — d t = Q(l—d/u);

время выполнения заказа t = Q/u; издержки заказа == (D/Q) К;

оптимальный размер заказа Q* =(2dK/h [(l-(d/u)])^1/2 = (2DK/H [(l-(d/u)])^1/2;

максимальный уровень запасов S* = Q*((l—(d/u))).

Модель 1.5 с количественными скидками. Для увеличения объема продаж компании часто предлагают количественные скидки своим покупателям. Количественная скидка — сокращенная цена на товар в случае покупки большого количества этого товара. Типичные примеры количественных скидок приведены в табл. 11.1.

Пусть I — доля издержек хранения в цене продукта с. Тогда h = (Ixc) и Q* =( 2dK/(Ixc))^l/2 — оптимальный размер заказа.

Пример 2. Рассмотрим пример, объясняющий принцип принятия решения в условиях скидки. Магазин "Медвежонок" продает игрушечные гоночные машинки. Эта фирма имеет таблицу скидок на машинки в случае покупок их в определенном количестве (табл. 11.1). Издержки заказа составляют 49 тыс .р. Годовой спрос на машинки равен 5000. Годовые издержки хранения в отношении к цене составляют 20%, или 0,2. Необходимо найти размер заказа, минимизирующий общие издержки.

Решение.

Рассчитаем оптимальный размер заказа для каждого вида скидок, т.е. Ql*, Q2* и Q3*, и получим Q1* = 700; Q2* = 714; Q3* = 718.

Так как Ql* — величина между 0 и 999, то ее можно оставить прежней. Q2* меньше количества, необходимого для получения скидки, следовательно, его значение необходимо принять равным 1000 единиц. Аналогично Q3* берем равным 2000 единиц. Получим Ql* = 700; Q2* = 1000; Q3* = 2000.

Далее необходимо рассчитать общие издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее значение.

Рассмотрим следующую таблицу.

Выберем тот размер заказа, который минимизирует общие годовые, издержки. Из таблицы видно, что заказ в размере 1000 игрушечных гоночных машинок будет минимизировать совокупные издержки.

3. ИМИТАЦИОННЫЕ МОДЕЛИ МАССОВОГО ОБСЛУЖИВАНИЯ

Имитация — это попытка дублировать особенности, внешний вид и характеристики реальной системы. Идея имитации состоит в:

1) математическом описании реальной ситуации,

2) изучении ее свойств и особенностей,

3)формировании выводов и принятии решений, связанных с воздействием на эту ситуацию и основанных на результатах имитации. Причем реальная система не подвергается воздействиям до тех пор, пока преимущества или недостатки тех или иных управленческих решений не будут оценены с помощью модели этой системы.

Метод Монте-Карло. Имитация с помощью метода Монте-Карло состоит из пяти простых этапов:

1. Установление распределения вероятностей для существенных переменных.

2. Построение интегрального распределения вероятности для всех переменных.

3. Установление интервала случайных чисел для каждой переменной.

4. Генерация случайных чисел.

5. Имитация путем многих попыток.

Проимитируем спрос на автомашины в салоне ЛОГОВАЗ в течение 10 последовательных дней. Для этого из таблицы случайных чисел мы выбираем значения, начиная из верхнего левого угла и двигаясь вниз в первом столбце.

39 — спрос за 10 дней. 39/10 = 3,9 — средний ежедневный спрос.

Пример 2. Груженые баржи, отправляемые вниз по Волге из индустриальных центров, достигают Астрахани. Число барж, ежедневно входящих в док, колеблется от 0 до 5. Вероятность прихода 0,1,...,5 барж показана в таблице. В этой же таблице указаны интегральные вероятности и соответствующие интервалы случайных чисел для каждого возможного значения.

Аналогичная информация дана о числе разгружаемых барж.

Имитация очереди на разгрузку барж в порту Астрахани представлена в следующей таблице.

4. ИМИТАЦИОННЫЕ МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ

Магазин электрооборудования Проводкова продает электрические дрели. В течение 300 дней Проводкой регистрировал дневной спрос на дрели. Распределение вероятностей величины спроса показано в таблице. Интегральные вероятности величин спроса показаны в четвертом столбце табл. В пятом столбце определены интервалы случайных чисел для определения возможных значений спроса.

Когда Проводков делает заказ, чтобы возобновить свои запасы электрических дрелей, его выполнение происходит с лагом в 1, 2 или 3 дня. Это означает, что время восстановления запаса подчиняется вероятностному распределению. В табл. показаны данные, позволяющие определить вероятности сроков выполнения заказов и интервалы случайных чисел на основе информации о 50 заказах.

Первая стратегия резервирования, которую хочет имитировать Проводков, — делать заказ в объеме 10 дрелей при запасе на складе 5 штук.

Реализуется четырехшаговый процесс имитации.

1. Каждый имитируемый день начинается с проверки, поступил ли сделанный заказ. Если заказ выполнен, то текущий запас увеличивается на величину заказа (в данном случае — на 10 единиц).

2. Путем выбора случайного числа генерируется дневной спрос для соответствующего распределения вероятностей.

3. Рассчитывается итоговый запас, равный исходному запасу за вычетом величины спроса. Если запас недостаточен для удовлетворения дневного спроса, спрос удовлетворяется, насколько это возможно. Фиксируется число нереализованных продаж.

4. Определяется, снизился ли запас до точки восстановления (в примере — 5 единиц). Если да, причем не ожидается поступления заказа, сделанного ранее, то делается заказ.

Первый эксперимент Проводкова. Объем заказа — 10 штук, точка восстановления запаса — 5 штук.

среднее число упущенных продаж = 2 упущенные продажи / 10 дней =0,2 шт./день.

Второй эксперимент Проводкова. Проводков оценил, что каждый заказ на дрели обходится ему в 10 000 р., хранение каждой дрели — в 5000 в день, одна упущенная продажа — в 80 000 р. Этой информации достаточно, чтобы оценить средние ежедневные затраты для этой стратегии управления запасами. Определим три составляющие затрат:

ежедневные затраты на заказы = (затраты на один заказ) х (среднее число заказов в день) = 10000 х 0,3 = 3000;

ежедневные затраты на хранение = (затраты на хранение одной единицы в течение дня) х (средняя величина конечного запаса) = 5000 х 4,1 = 20500;

ежедневные упущенные возможности = (прибыль от упущенной продажи) х (среднее число упущенных продаж в день) = 80000 х 0,2 = 16000,

общие ежедневные затраты = затраты на заказы + затраты на хранение + упущенные продажи = 39500.

5. ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ   1. Основные понятия

Производственная функция - это функция, независимая переменная которой принимает значения объемов затрачиваемого или используемого ресурса (фактора производства), а зависимая переменная - значения объемов выпускаемой продукции

Точное толкование понятий затрачиваемого (или используемого) ресурса и выпускаемой продукции, а также выбор единиц их измерения зависят от характера и масштаба производственной системы, особенностей решаемых (с помощью ПФ) задач (аналитических, плановых, прогнозных), наличия исходных данных.

На микроэкономическом уровне затраты и выпуск могут измеряться как в натуральных, так и в стоимостных единицах (показателях). Годовые затраты труда могут быть измерены в человеко-часах (объем человеко-часов - натуральный показатель) или в рублях выплаченной заработной платы (ее величина - стоимостный показатель); выпуск продукции может быть представлен в штуках или в других натуральных единицах (тоннах, метрах и т.п.) или в виде своей стоимости.

На макроэкономическом уровне затраты и выпуск измеряются, как правило, в стоимостных показателях и представляют собой стоимостные (ценностные) агрегаты, т.е. суммарные величины произведений объемов затрачиваемых (или используемых) ресурсов и выпускаемых продуктов на их цены.

Производственная функция нескольких переменных - это функция, независимые переменные которой принимают значения объемов затрачиваемых или используемых ресурсов (число переменных л равно числу ресурсов), а значение функции имеет смысл величин объемов выпуска:

При построении ПФ для региона или страны в целом в качестве величины годового выпуска Y (будем обозначать объем выпуска, или дохода, на макроуровне большой буквой) чаще берут совокупный продукт (доход) региона или страны, исчисляемый обычно в неизменных, а не в текущих ценах, в качестве ресурсов рассматривают основной капитал (х₁ (=К) - объем используемого в течение года основного капитала), живой труд (х₂ (=L) - количество единиц затрачиваемого в течение года живого труда), исчисляемые обычно в стоимостном выражении. Таким образом строят двухфакторную f(х₁, х₂), или Y=f{K,L). От двухфакторных ПФ переходят к трехфакторным. В качестве третьего фактора иногда вводят объемы используемых природных ресурсов. Кроме того, если ПФ строится по данным временных рядов, то в качестве особого фактора роста производства может быть включен технический прогресс.

ПФ у =f(х₁, х₂) называется статической, если ее параметры и ее характеристика f не зависят от времени t, хотя объемы ресурсов и объем выпуска могут зависеть от времени t, т.е. могут иметь представление в виде временных рядов.

Пример . Для моделирования отдельного региона или страны в целом (т.е. для решения задач на макроэкономическом, а также и на микроэкономическом уровне) часто используется ПФ вида у = a₀x₁^a₁x₂^a₂, где а_0, а₁, а₂ - параметры ПФ. Это положительные постоянные (часто а₁ + а₂ = 1). ПФ только что приведенного вида называется ПФ Кобба-Дугласа (ПФКД) по имени двух американских экономистов, предложивших ее использовать в 1929 г. ПФКД активно применяется для решения разнообразных теоретических и прикладных задач благодаря своей структурной простоте. ПФКД принадлежит к классу так называемых мультипликативных ПФ (МПФ). В приложениях ПФКД х₁ = K равно объему используемого основного капитала (объему используемых основных фондов - в отечественной терминологии), x₂=L - затратам живого труда, тогда ПФКД приобретает вид, часто используемый в литературе:

 

Пример . Линейная ПФ (ЛПФ) имеет вид: у= а₀ + а₁х₁ + a₂x₂. (двухфакторная) и у= а₀ + а₁х₁ + a₂x_{2+ …+}a_nx_n(многофакторная). ЛПФ принадлежит к классу так называемых аддитивных ПФ (АПФ). Переход от мультипликативной ПФ к аддитивной осуществляется с помощью операции логарифмирования. Для двухфакторной мультипликативной ПФ

Выполняя обратный переход, из аддитивной ПФ получим мультипликативную ПФ.

Если а₁ + а₂ = 1, то ее можно записать в несколько другой форме:

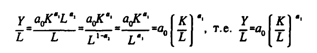
называются соответственно производителностью труда и капиталовооруженностью труда. Используя новые символы, получим

т.е. из двухфакторной ПФКД получим формально однофакторную ПФКД. В связи с тем, что 0 < a₁< 1, из последней формулы следует, что производительность труда растет медленнее его капиталовооруженности. Однако этот вывод справедлив для случая статической ПФКД в рамках существующих технологии и ресурсов.

Отметим здесь, что дробь Y / K — называется производительностью капитала или капиталоотдачей, обратные дроби K / Y и L / Y называются соответственно капиталоемкостью и трудоемкостью выпуска.

ПФ называется динамической, если:

1) время t фигурирует в качестве самостоятельной переменной величины (как бы самостоятельного фактора производства), влияющего на объем выпускаемой продукции;

2) параметры ПФ и ее характеристика f зависят от времени t.

Отметим, что если параметры ПФ оценивались по данным врменных рядов (объемов ресурсов и выпуска) продолжительностью T₀ лет (т.е. базовый промежуток для оценки параметров имеет продолжительность T₀ лет), то экстраполяционные расчеты по такой ПФ

 следует проводить не более чем на T₀ / 3 лет вперед (т.е. промежуток экстраполяции должен иметь продолжительность не более чем T₀/3 лет).

При построении ПФ научно-технический прогресс (НТП) может быть учтен с помощью введения множителя НТП е^pt, где параметр (число) p(p>0) характеризует темп прироста выпуска под влиянием НТП:

Эта ПФ - простейший пример динамической ПФ; она включает нейтральный, то есть не материализованный в одном из факторов, технический прогресс. В более сложных случаях технический прогресс может воздействовать непосредственно на производительность труда или капиталоотдачу: Y(t) = f(A(t)-L(t), K(t)) или Y(t) = f(A(t) K(t), L(t)). Он называется, соответственно, трудосберегающим или капиталосберегающим НТП.

Пример .. Поиведем вариант ПФКД с учетом НТП v(t} =

Выделение существенных видов ресурсов (факторов производства) и выбор аналитической формы функции f называется спецификацией ПФ .

Преобразование реальных и экспертных данных в модельную информацию, т.е. расчет численных значений параметров ПФ на базе статистических данных с помощью регрессионного и корреляционного анализа, называется параметризацией ПФ .

Проверка истинности (адекватности) ПФ называется ее верификацией.

Выбор аналитической формы ПФ (т.е. спецификация) диктуется прежде всего теоретическими соображениями, которые должны явно (или даже неявно) учитывать особенности взаимосвязей между конкретными ресурсами (в случае микроэкономического уровня) или экономических закономерностей (в случае макроэкономического уровня), особенности реальных или экспертных данных, преобразуемых в параметры ПФ (т.е. особенности параметризации). На спецификацию и параметризацию в процессе совершенствования ПФ оказывают влияние результаты верификации ПФ. Отметим здесь, что оценка параметров ПФ обычно проводится с помощью метода наименьших квадратов.

2. Предельные (маржинальные) и средние значения производственной функции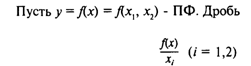

называется средней производительностью i-го ресурса (фактора производства) (СПФ) или средним выпуском по i-му ресурсу (фактору производства). Символика: А_i=f(x)/x_i.

Напомним, что в случае двухфакторной ПФКД  для средних производительностей Y/K и Y/L основного капитала и труда были использованы соответственно термины капиталоотдача и производительность труда. Эти термины используют и применительно к любым двухфакторным ПФ, у которых х₁=К и x₂=L.

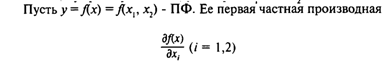
называется предельной (маржинальной) производительностью i-го ресурса (фактора производства) (ППФ) или предельным выпуском по i-му ресурсу (фактору производства). Символика: M_i=df(x)/dx_i.

Следовательно, ППФ (приближенно) показывает, на сколько единиц увеличится объем выпуска у, если объем затрат х i-го ресурса вырастает на одну (достаточно малую) единицу при неизменных объемах другого затрачиваемого ресурса.

Отношение предельной производительности M_i i-го ресурса к его средней производительности А_iназывается (частной) эластичностью выпуска по i-му ресурсу (по фактору производства) (ЭВФ). Символика:

Сумма Е₁ + Е₂ = Е_x называется эластичностью производства.

Е (приближенно) показывает, на сколько процентов увеличится выпуск у, если затраты i-го ресурса 1 увеличатся на один процент при неизменных объемах другого ресурса.

Обратим внимание на то, что i - номер заменяемого ресурса, j -номер замещающего ресурса. Используется также термин: предельная технологическая норма замены (замещения) i-ого ресурса (фактора производства) j-м ресурсом (фактором производства). Приведем более краткий (но менее точный) термин: (предельная) норма замены (замещения) ресурсов.

Непосредственно проверяется, что для двухфакторной ПФ справедливо равенство

т.е. (предельная) норма замены первого ресурса вторым равна отношению эластичностей выпуска по первому и второму ресурсам, умноженному на отношение объема второго ресурса к объему первого ресурса. Если х₁ = К, х₂= L, то отношение x₁/x₂=K/L называется капиталовооруженностью труда. В этом случае (предельная) норма замены основного капитала трудом равна отношению эластичностей выпуска по основному капиталу и труду, поделенному на капиталовооруженность труда.

Пусть ПФ - двухфакторная. При постоянном выпуске у и малых приращениях Дх₁, и Дх₂, имеем приближенное равенство

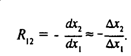
Предельная норма замены ресурсов R₁₂ (приближенно) показывает, на сколько единиц увеличатся затраты второго ресурса (при неизменном выпуске у = а), если затраты первого ресурса уменьшатся на одну (малую) единицу.

3. Пример

Имеются статистические данные по производственному объединению “Угледобыча":

Условное время t		Средн. годовая списочн. численность Х1, тыс .чел	Балансовая стоим. основных фондов Х2, млн.грн.	Валовая продукция Y, млн.грн
1	3,6		100	416
2	4,1		105	464
3	3,8		90	400
4	3,2		110	432
5	3,5		125	480

Балансовая стоимость основных фондов и валовая продукция производственного объединения даны с учетом пересчета по индексу цен.

Вычислить производственную функцию Кобба-Дугласа; определить коэффициенты эластичности валовой продукции по списочной численности и стоимости основных фондов, а также предельные производительности по этим факторам. По результатам расчетов сформулировать выводы.

Решение:

Производственная функция Кобба-Дугласа имеет следующий вид

 

где b₀ , b₁ , b₂ – параметры уравнения.

Для оценки параметров прологарифмируем уравнение и выполним замену переменных:

ln y =ln b₀ + b₁ ln x₁ + b₂ ln x₂

b’₀= ln b₀ , y’= ln y, x’₁= ln x₁, x’₂= ln x₂.

В результате этих преобразований получим линейную модель

y’= b’₀+ b₁ x’₁+ b₂ x’₂.

Для определения значений коэффициентов этой модели прологарифмируем исходные значения у и х₁, х₂, а затем используем метод наименьших квадратов.

В результате вычислений с помощью функции ЛИНЕЙН пакетаEXCEL получим

b₁ = 0,424, b₂ = 0,680,

ln b₀ = 2,369 откуда b₀= 10,690.

Следовательно, производственная функция Кобба-Дугласа имеет следующий вид

Y=10,690X₁^0,424X₂^0,68.

Коэффициент эластичности валовой продукции по списочной численности (по х1) равен b₁ = 0,424.

Коэффициент эластичности валовой продукции по стоимости основных фондов (по х2) равен b₂ = 0,680.

Следовательно, можно сделать вывод, что при увеличении списочной численности на 1% объём валовой продукции увеличится на 0,424% , а при увеличении стоимости основных фондов на 1% объём валовой продукции увеличится на 0,68%.

Предельная производительность по списочной численности равна

M₁ = b₁* Y / X₁ = 0,424* Y / X₁= 0,424* 10,690X₁ ^–0,576 X₂^0,68 ,

где Y / X₁- производительность труда.

Предельная производительность по стоимости основных фондов равна

M₂ = b₂* Y / X₂ = 0,680* Y / X₂ =0,680* 10,690X₁^0,424X₂ ^–0,32 ,

где Y / X₂ -фондоотдача.

5. Применение аппарата теории игр для анализа проблем микроэкономики 1. Основные понятия

Важным случаем в теории игр является ситуация, когда выигрыш одного из игроков равен проигрышу другого, т.е. налицо прямой конфликт между игроками. Классическими примерами здесь являются ситуации, где, с одной стороны, имеется один покупатель, с другой - продавец (ситуация монополия-монопсония). Подобные игры называются играми с нулевой суммой, или антагонистическими играми.

В зависимости от возможности предварительных переговоров между игроками различают кооперативные и некооперативные игры.

Игра, в которой игроки не могут координировать свои стратегии подобным образом, называется некооперативной. Очевидно, что все антагонистические игры могут служить примером некооперативных игр.

Кооперативной игрой называется игра с ненулевой суммой, в которой игрокам разрешается обсуждать перед игрой свои стратегии и договариваться о совместных действиях, т.е. игроки могут образовывать коалиции. Основная задача в кооперативной игре состоит в дележе общего выигрыша между членами коалиции. Примером кооперативной игры может служить ситуация образования коалиций в парламенте для принятия путем голосования решения, так или иначе затрагивающего интересы участников голосования.

Проблемы рыночного взаимодействия близки к проблемам теории игр и могут быть эффективно описаны и исследованы в ее терминах.

Представим себе экономику, в которой имеется два субъекта: Игрок1 (Фирма1) и Игрок2 (Фирма2), и два товара х₁ и х₂, (естественно, число игроков и товаров может быть большим, но в случае 2х2 все введенные понятия имеют наглядную интерпретацию.)

Каждый из игроков имеет свою функцию полезности, (функцию дохода) заданную на наборе товаров: h₁(х₁,х₂), h₂(х₁,х₂). В начале игры в экономике имеется общее количество Х₁ первого товара и X₂ - второго товара. Предположим, что это начальное количество благ как-то распределено между игроками: 1-й Игрок обладает количеством Х₁¹первого товара и X₂¹ - второго, 2-й Игрок - количествами X₁² и X₂², 1-го и 2-го товаров соответственно, так что X₁¹ + X₁² =Х₁ и X₂¹ + X₂²=X₂.

Встают вопросы: могут ли игроки путем обмена имеющимися у них товарами улучшить свое положение, т.е. увеличить значение функций полезности h₁, и h₂, по сравнению с начальными уровнями h₁(Х₁¹, X₂¹ ) и h₂(X₁²,X₂²); каковы свойства такого решения?

Для наглядного представления экономики с двумя игроками и двумя товарами традиционно используется так называемый ящик Эджворта (рис. 1). 1-го Игрока, пунктирными - кривые безразличия 2-го Игрока)

В ящике Эджворта длина горизонтальной оси, соответствующей первому товару, равна общему количеству этого товара Х₁, длина вертикальной оси - общему количеству товара X₂. Выделенное пространство является множеством всех возможных распределений имеющихся товаров между двумя игроками. Нижний левый угол считается началом координат для 1-го Игрока, верхний правый угол - началом координат для 2-го Игрока.

На выделенном пространстве представлены также два множества кривых безразличия (линий уровня функций выигрыша), принадлежащих каждому из игроков. При этом точка начального распределения товаров имеет координаты (Х₁¹, X₂¹ ) в системе отсчета 1-го Игрока (и, соответственно, (X₁²,X₂²); в системе отсчета 2-го Игрока).

2. Парето-оптимальное множество решений

Рассмотрим для начала проблему эффективного распределения товаров между игроками. Единственным требованием к распределению, которое мы можем предъявить на начальном этапе анализа, является требование Парето-оптимальности. Распределение называется Парето-оптимальным, если положение ни одного из игроков нельзя улучшить, не ухудшая при этом положение его партнера.

Множество Парето-оптимальных распределений может быть наглядно представлено с помощью ящика Эджворта. В случае 2-х игроков Парето-оптимальное решение может быть найдено с помощью фиксации уровня полезности одного из игроков (скажем, Игрока 2) и поиска максимума функции полезности другого игрока.

В терминах ящика Эджворта это означает, что необходимо найти такую точку на фиксированной кривой безразличия Игрока 2, в которой Игрок 1 получает максимум своей функции полезности.

Очевидно, что такой точкой является точка, где кривые безразличия касаются друг друга, так как в противном случае Игрок 1 может, продвигаясь вдоль фиксированной линии уровня Игрока 2 внутрь, увеличить значение своей функции полезности (рис. 2).

Опираясь на этот факт, можно показать, что множество Парето-оптимальных распределений в ящике Эджворта будет множеством всех точек, в которых кривые безразличия Игрока 1 и Игрока 2 касаются друг друга (рис. 3).

Множество Парето-оптимальных распределений в пространстве товаров называется контрактным множеством, поскольку игрокам в общем случае имеет смысл договариваться между собой именно на этом наборе эффективных распределений.

3. Переговорное множество решений

Рассмотрим теперь ситуацию, когда каждый игрок обладает некоторым начальным количеством каждого из товаров. Встает вопрос: может ли это начальное распределение быть улучшено путем обмена товарами между игроками? Исследуем эту проблему с помощью ящика Эджворта.

Пусть (Х1 1, X21) - точка начального распределения товаров; проведем через эту точку кривые безразличия для Игрока 1 и Игрока 2 (рис. 4).

Если две кривые не касаются друг друга (т.е. если начальное распределение не является Парето-оптимальным), то в своем пересечении они образуют область, двигаясь внутрь которой каждый из игроков может увеличивать значение обеих функций полезности. При этом. как легко показать, часть контрактного множества оказывается внутри области, образованной проведенными кривыми безразличия.

Игрокам имеет смысл вести переговоры относительно распределений, находящихся на контрактном множестве, а с учетом начального распределения - относительно участка контрактного множества, заключенного между двумя кривыми безразличия.

Эти кривые называются линиями угрозы, а выделяемый ими участок на контрактном множестве - переговорным множеством.

Линии угрозы в данном случае означают, что за их пределами (т.е. ниже и левее исходной кривой безразличия для Игрока 1 и выше и правее кривой безразличия для Игрока 2) какому-либо из игроков становится незачем вести переговоры - ему лучше (или, по крайней мере, не хуже) оставаться в ситуации начального распределения.

Для того чтобы переместиться на переговорное множество, в случае рис.4 Игрок 1 должен передать (продать) некоторое количество имеющегося у него товара 1 Игроку 2 в обмен на определенное количество товара 2, имеющегося у Игрока 2.

На переговорном множестве выделяется точка решения Нэша N, в которой достигается максимум произведения приращений дохода каждого из игроков по сравнению с доходом, который может быть получен без вступления в коалицию.

В результате проведенного анализа можно сделать вывод, что игроки могут улучшить свое первоначальное положение, обмениваясь товарами, и Игроку 1 выгодно уступить Игроку 2 некоторое количество товара 1 в обмен на товар 2.

4. Задача о дуополии

Рассмотрим в заключение решение задачи о дуополии.

В этой задаче две фирмы сталкиваются с проблемой удовлетворения спроса на некоторый товар. Объем спроса зависит от уровня назначаемых цен и описывается функцией d(р) (ей соответствует нисходящая линия на рис.5). Объем предложения товара каждой из фирм также зависит от уровня цен и в микроэкономике описывается функциями предложения s1(p}, s2(р); эти функции определяются уровнем предельных издержек каждой из фирм.

Предположим для простоты, что Фирма 1 и Фирма 2 имеют одинаковые функции предложения s1(p)=s2(p) .

Поиск решения в задаче о дуополии (т.е. определение уровня цен и объемов предложения каждой из фирм) базируется на принципах, общих для решения задач теории игр: каждая из сторон располагает информацией о себе и своем партнере (в данном случае - о функциях предложения каждой из фирм), об условиях игры (в данном случае - о функции спроса) и действует, исходя из предположения, что ее партнер располагает такой же информацией и действует рационально (т.е. стремится максимизировать свой доход).

Если Фирма 1 назначит цену на предлагаемый ею товар р1, а Фирма 2 примет эту цену, то Фирма 1 сможет продать объем товара, равный

Функция r1(p) называется остаточной функцией спроса, с которой сталкивается Фирма 1 (рис.5). Поскольку величина r1, описывает объем спроса, приходящийся только на продукцию Фирмы 1, то она получит максимум дохода, полностью удовлетворив этот спрос, т.е. при условии, что

В итоге Фирма 1, опираясь на имеющуюся у нее информацию, решает задачу поиска равновесного уровня цен р , при которых

Аналогичную задачу поиска равновесных цен решает Фирма 2

Учитывая, что s1(p)=s2(p), мы получим, что в ситуации равновесия

а доход каждой из фирм будет равен

Таким образом, в задаче о дуополии фирмы должны найти такой уровень цен р*, при котором они смогут полностью удовлетворить спрос на продукцию d(p*), распределив между собой производство этой продукции поровну и получив при этом одинаковый доход. Уровень равновесных цен и объем предложения каждой из фирм определяют в данной задаче ситуацию равновесия по Нэшу.