Використання модульної арифметики. Обчислення з многочленами. Методи множення. Складність обчислень

Використання модульної арифметики. Обчислення з многочленами. Методи множення. Складність обчислень

Ефективний шлях багаторазового зведення за модулем – використання методу Монтгомері, який було запропоновано в 1985 році. Цей метод особливо ефективний при апаратній реалізації алгоритмів. Дуже зручно відмовитися від операцій множення і ділення та замінити їх операціями додавання. Метод полягає в наступному.

Нехай  – непарне число, потрібно помножити лишки.

Розглянемо алгоритм: R = 0;

for i = 0 until i < n do begin

if a_i = 1 then R = R + B;

if R - непарне then R = R + N;

R = R / 2;

end

if R ³ N then R = R - N.

Суть даного алгоритму в тому, що в силу рівності

A =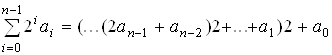

множення числа В на число А зводиться до обчислення

AB =

зведення модуль многочлен множення

Воно виконується за  кроків, на кожному з яких здійснюється додавання до поточного значення  значення ,  з наступним діленням на . Завдяки цьому діленню отримані значення завжди знаходяться в інтервалі . У результаті роботи даного алгоритму виходить число . Тепер для одержання числа  необхідно застосувати ще один раз даний алгоритм до чисел  і . Оскільки число  обчислюється за допомогою зрушень і відрахувань зі складністю  двійкових операцій (його можна обчислити заздалегідь і зберігати отримане значення), а алгоритм також виконується за  операцій, тo загальна трудомісткість обчислення добутку оцінюється величиною  двійкових операцій.

Наприклад:

А = 1´2⁰ + 0´2¹ + 1´2² + 0´2³ + 1´2⁴ = 1 + 4 + 16 = 21 (10101) У = 18 N = 41

Зрозуміло, що АВ(mod N) = 21´18 (mod 41) = 9.

Обчислимо добуток цих чисел за допомогою вищезазначеного алгоритму.

R = 0 a₀ = 1 R = R + B = 0 + 18 = 18;

R - парне;

R = R / 2 = 9.

2. a₁ = 0;

R - непарне;

R = R + N = 9 + 41 = 50;

R = R / 2 = 25;

a₂ = 1 R = R + B = 25 + 18 = 43;

R – непарне;

R = R + N = 43 + 41 = 84;

R = R / 2 = 42;

a₃ = 0; R – непарне; R = R + N = 1 + 41 = 42;

R = R / 2 = 21;

a₄ = 1 R = R + B = 21 + 18 = 39;

R - непарне;

R = R + N = 39 + 41 = 80;

R = R / 2 = 40.

Це ми одержали 2^-n AB(mod N)

Тепер ми повинні ще раз скористатися цим алгоритмом для обчислення АВ (mod N).

 

A’ = 2²ⁿ (mod N) = 2^{2 ´5}(mod N) = 1024(mod 41) = 40 = 0´2⁰ + 0´2¹ + 0´2² + 1´2³ + 0´2⁴ + 1´2⁵

B ’= 40;

N = 41.

R = 0 a₀ = 0 R - парне;

R = R / 2 = 0.

a₁ = 0; R - парне;

R = R / 2 = 0;

a₂ = 0 R - парне;

R = R / 2 = 0;

a₃ = 1; R = R + B = 0 + 40 = 40;

R - парне;

R = R / 2 = 20;

a₄ = 0; R - парне;

R = R / 2 = 10;

6. a₅ = 1; R = R + B = 10 + 40 = 50;

R = R - N = 50 - 41 = 9.

Звертання

Для заданого числа , , знаходимо за допомогою розширеного алгоритму Евкліда числа  і , що задовольняють рівності . Якщо , тo як зворотний можна взяти . Таким чином, звертання в кільці лишків можна виконати за  бітових операцій.

Ділення

Оскільки , то ділення у кільці лишків виконується зі складністю .

Обчислення з многочленами

Між обчисленнями в кільці многочленів над довільним кільцем  і в кільці цілих чисел, записаних у будь-якої системи числення багато спільного. Вони виконуються за схожими формулами, а різниця лише в тому, що для чисел необхідно враховувати знаки переносу від молодших розрядів до старших, у той час як у випадку многочленів ніяких переносів при операціях з коефіцієнтами не виникає – і вихідні величини і значення лежать у кільці .

Складність операцій з многочленами, звичайно, оцінюють кількістю ариф-метичних операцій кільця , які виконуються над його коефіцієнтами. Якщо відомо бітову складність операцій у полі, то можна оцінити результуючу бітову складність операцій з многочленами. Щоб відрізняти арифметичну складність від бітової в оцінках ми використовуватимемо символи  і .

Обчислення значень многочленів.

Нехай  – довільне кільце. Розглянемо добре відомий алгоритм Руфіні - Горнера для обчислення значень многочлена над кільцем  у точці.

Останнє число ,і буде шуканим значенням многочлена. Арифметична складність алгоритму, мабуть, дорівнює . Бітову складність у випадку, коли кільце  розглядається як кільце цілих чисел, можна оцінити виразом , де через  позначений максимум із двох чисел: числа двійкових знаків у запису найбільшого з коефіцієнтів і числа  , а число  означає число двійкових знаків у запису найбільшого з чисел  . У такий спосіб виходить оцінка

Алгоритм Руфіні-Горнера дозволяє отримати не тільки значення . Як показує наступна теорема, величини  є в точності коефіцієнтами многочлена, що є лишком від ділення многочлена  на .

Теорема 1

Справедлива рівність

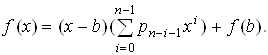
Доведення

Маємо

Методи множення

Для зручності ми думатимемо, що ми оперуємо із цілими числами, вираженими у двійковій системі числення. У нас є два -розрядних числа  і , то можна записати

де  – ²найбільш значуща половина² числа , а  – ²найменш значуща половина²; подібним же чином , .

Ця формула зводить задачу множення - розрядних чисел до трьох операцій множення  розрядних чисел:  плюс деякі прості операції зсуву і додавання. Цю формулу можна використовувати для множення з подвійною точністю, коли результат потрібно отримати із четверною точністю. За допомогою цієї формули можна визначити деякий рекурсивний процес для множення, значно більш швидкий, ніж уже знайомий нам метод, коли – велике та час виконання порядку .

Якщо – час, необхідне для виконання множення -розрядних чисел, то ми маємо

 для деякої константи , оскільки в правій частині співвідношення потрібно виконати тільки три операції множення плюс деякі операції додавання і зрушення. З останнього співвідношення за індукцією випливає, що

,

якщо вибрати – достатньо великим, для того, щоб ця нерівність виконувалася при , отримаємо

Тобто час, затрачуваний на множення, можна скоротити з величини порядку  до величини порядку , і, звичайно, при великому  цей алгоритм набагато швидше.

Схожий, але більш складний метод виконання множення із часом порядку  був уперше запропонований А. Карацубою.

Час виконання можна скоротити ще більше, якщо помітити, що тільки що розглянутий метод є окремим випадком (при ) більш загального методу, що дає

для будь-якого фіксованого . Цей більш загальний метод можна отримати в такий спосіб. Розіб'ємо

 і

на  частин:

 

де кожне  і кожне  є  розрядними числами. Розглянемо многочлени

,

і покладемо

.

Оскільки  і , то ми маємо , і тому, якщо знати коефіцієнти , можна легко обчислити . Завдання полягає в тому, щоб знайти гарний спосіб обчислення коефіцієнтів , виконуючи лише  операцій множення - розрядних чисел плюс деякі додаткові операції, для яких час виконання пропорційно .

Цього можна досягти, обчислюючи

.

Коефіцієнти будь-якого многочлена степені можна записати у вигляді лінійної комбінації значень цього многочлена в  різних точках. Час, необхідний для узяття такої комбінації, якнайбільше пропорційно . У дійсності добутком  є, точно кажучи, не добутками -розрядних чисел, а добутками чисел, розряд яких не перевищує , де – фіксована величина, що залежить від . Легко скласти програму множення для  – розрядних чисел, що вимагає виконання лише  операцій, тому що при фіксованому  два добутки -розрядних чисел на -розрядні можна одержати за  операцій. Можна показати, що для цього методу

.

Теорема 2

Для кожного  існує така постійна  і такий алгоритм множення, що число елементарних операцій , які необхідно виконати, щоб помножити два - розрядних числа, відповідає оцінці . Ця теорема ще не найкращий результат. Для практичних цілей великий недолік, що метод різко ускладнюється при  тобто . Ця теорема незадовільна й з теоретичної точки зору, тому що в ній не повною мірою використовується лежачий у її основі метод багаточленів.

Перш ніж розглянути алгоритм Тоома-Кука, розберемо один приклад. На цьому прикладі не можна побачити ефективність методу, оскільки ми маємо справу з невеликими числами. Але можна побачити деякі корисні спрощення, що застосовні в загальному випадку.

Приклад

Припустимо, нам потрібно помножити  на .

У двійковій системі числення  на .

Нехай .

Багаточлени  , .

Звідси знаходимо :

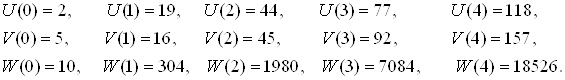 (3.1)

Тепер, використовуючи п'ять останніх величин, знайдемо п'ять коефіцієнтів багаточлена .

Для перебування коефіцієнтів багаточлена

при заданих значеннях  можна скористатися одним цікавим невеликим алгоритмом. Спочатку запишемо

,

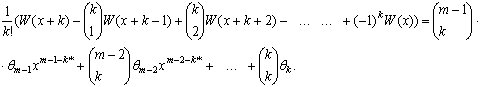
Позначаючи ліву частину виразу через  ми бачимо, що

Отже, коефіцієнти  можна обчислити за допомогою дуже простого методу, якому можна продемонструвати для багаточлена , визначеного співвідношеннями (3.1):

Крайній стовпчик складається із заданих значень ; щоб одержати -ту колонку, потрібно обчислити різниці між сусідніми величинами попереднього стовпчика і розділити їх на . Коефіцієнти  розташовуються в колонках зверху; так, , тому ми маємо

У загальному вигляді можна записати

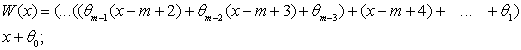
ця формула показує, яким чином з коефіцієнтів  можна отримати коефіцієнти :

Послідовно виходять коефіцієнти багаточленів

 

Відповідно до останньої таблиці ми маємо

Отже, відповіддю до нашої вихідної задачі буде  де  виходить у результаті дій додавання і зрушення. Крім того, якщо коефіцієнти багаточлена  – ненегативні, то такими будуть і числа , а тоді всі проміжні результати, одержувані в процесі проведення обчислення, є ненегативними.