Розробка функціонального алгоритму
Пам'ять – зберігає код стану (Q);
Формування схеми автомата Мура
Позначаємо вхід початкових та кінцевих станів;
Синтез дешифратора та його синтез у заданий базис
Синтез автоматів з програмованою логікою
Синтез автомата з природною адресацією команд
ПОРІВНЯЛЬНА ХАРАКТЕРИСТИКА АВТОМАТІВ
Навигация
Синтез автомата з природною адресацією команд
Синтез керуючих автоматів
26838
знаков
19
таблиц
22
изображения
3.2 Синтез автомата з природною адресацією команд
У реальних мікропрограмах часто зустрічаються ситуації, коли маються досить довгі сплетіння операторних вершин. У цьому випадку можлива організація схеми, коли безумовний перехід не задається, а виконується нарощуванням адреси мікрокоманди. Таким чином вдається зменшити довжину мікрокоманди за рахунок формування вихідних сигналів і аналізу вхідних сигналів у різні моменти часу. Для цього в автоматах із природною адресацією використовується два формати мікрокоманд:
- операторна
- умовна
|
|
|
|
|
 | |||
| |||
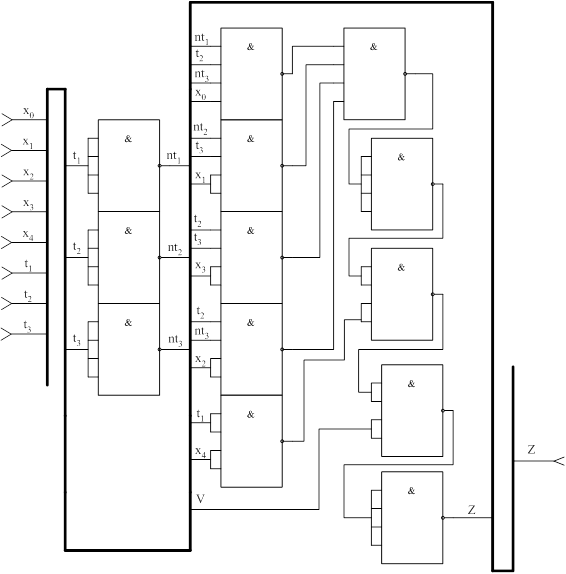
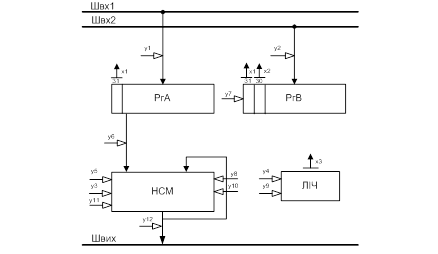
Рис. 3.4 – Структурна схема автомата з природною адресацією
Аналіз схеми:
У регістрі мікрокоманд зберігатися поточне МК, якщо це операторна МК, то працює схема формування вихідних сигналів і в операційний автомат попадає y.
При цьому схема аналізу Х формує Z, що змушує адресу, що зберігається в лічильнику збільшитися на одиницю.
Якщо в регістрі МК умовна МК, то вихідний сигнал не формується, а схема аналізу Х формує Z, у залежності від значення Z:
якщо Z=1, то до значення лічильника команд додається 1,
якщо Z=0, то в лічильник попадає адреса мікрокоманди з поля b.
Порядок формування змісту ROM такий же як в автоматі з примусовою адресацією мікрокоманд.
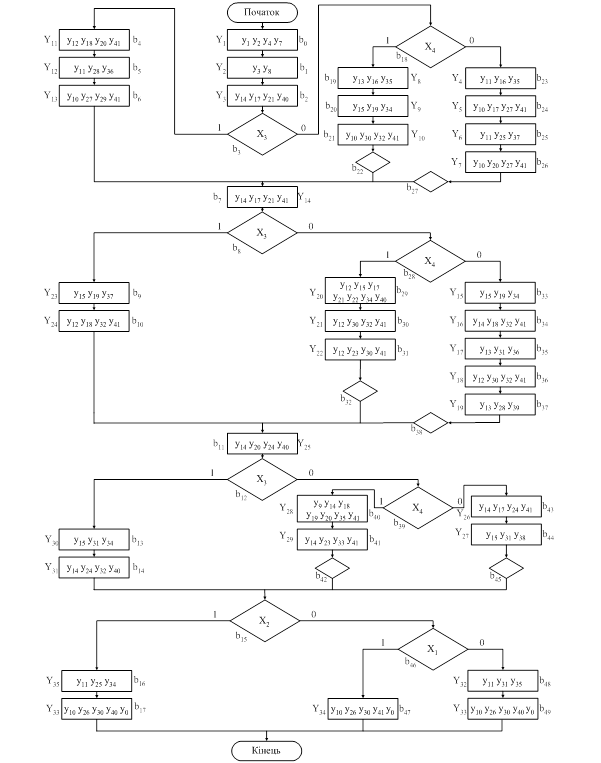
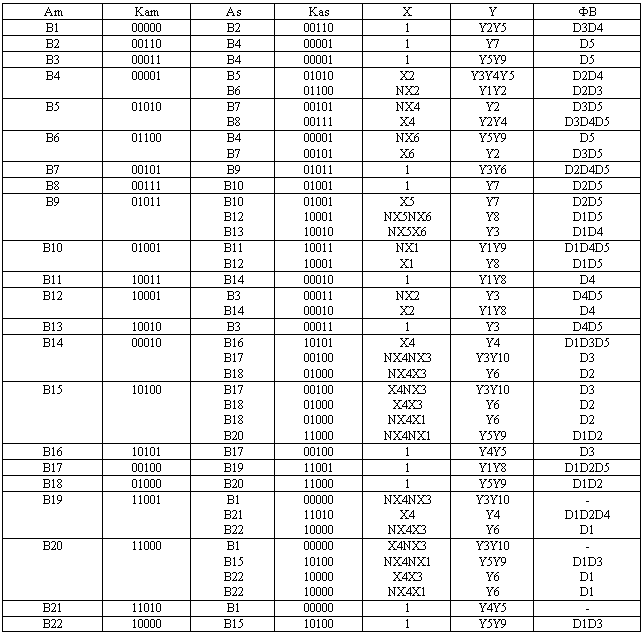
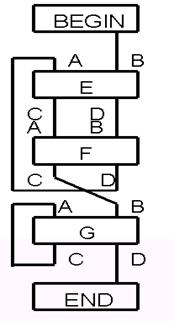
Рис. 3.5 – Граф-схема автомата з природною адресацією команд
Табл. 3.5 – Структура переходів для автомата з природною адресацією команд
| № п/п | Адреса b b1 b2 b3 b4 b5 b6 | 0 | 1 . . . 6 | Перехід | |
| 1 | 1 ... 3 | 4 . . . 9 | |||
| 1 | 000000 | 0 | 000001 | b0 → b1 | |
| 2 | 000001 | 0 | 000010 | b1 → b2 | |
| 3 | 000010 | 0 | 000011 | b2 → b3 | |
| 4 | 000011 | 1 | 011 | 010010 | b2 → |
| 5 | 000100 | 0 | 001011 | b4 → b5 | |
| 6 | 000101 | 0 | 001100 | b5 → b6 | |
| 7 | 000110 | 0 | 001101 | b6 → b7 | |
| 8 | 000111 | 0 | 001110 | b7 → b14 | |
| 9 | 001000 | 1 | 011 | 011100 | b8 → |
| 10 | 001001 | 0 | 010111 | b9 → b10 | |
| 11 | 001010 | 0 | 011000 | b10 → b11 | |
| 12 | 001011 | 0 | 011001 | b11 → b12 | |
| 13 | 001100 | 1 | 011 | 100111 | b12 → |
| 14 | 001101 | 0 | 011110 | b13 → b14 | |
| 15 | 001110 | 0 | 011111 | b14 → b15 | |
| 16 | 001111 | 1 | 010 | 101110 | b15 → |
| 17 | 010000 | 0 | 100011 | b16 → b17 | |
| 18 | 010001 | 0 | 100001 | b17 → кінець | |
| 19 | 010010 | 1 | 100 | 010111 | b18 → |
| 20 | 010011 | 0 | 001000 | b19 → b20 | |
| 21 | 010100 | 0 | 001001 | b20 → b21 | |
| 22 | 010101 | 0 | 001010 | b21 → b22 | |
| 23 | 010110 | 1 | 000 | 000111 | b22 → БП b7 |
| 24 | 010111 | 0 | 000100 | b23 → b24 | |
| 25 | 011000 | 0 | 000101 | b24 → b25 | |
| 26 | 011001 | 0 | 000110 | b25 → b26 | |
| 27 | 011010 | 0 | 000111 | b26 → b27 | |
| 28 | 011011 | 1 | 000 | 000111 | b27 → БП b7 |
| 29 | 011100 | 1 | 100 | 100001 | b28 → |
| 30 | 011101 | 0 | 010100 | b29 → b30 | |
| 31 | 011110 | 0 | 010101 | b30 → b31 | |
| 32 | 011111 | 0 | 010110 | b31 → b32 | |
| 33 | 100000 | 1 | 000 | 001011 | b32 → БП b11 |
| 34 | 100001 | 0 | 001111 | b33 → b34 | |
| 35 | 100010 | 0 | 010000 | b34 → b35 | |
| 36 | 100011 | 0 | 010001 | b35 → b36 | |
| 37 | 100100 | 0 | 010010 | b36 → b37 | |
| 38 | 100101 | 0 | 010011 | b37 → b38 | |
| 39 | 100110 | 1 | 000 | 001011 | b38 → БП b11 |
| 40 | 100111 | 1 | 100 | 101011 | b39 → |
| 41 | 101000 | 0 | 011100 | b40 → b41 | |
| 42 | 101001 | 0 | 011101 | b41 → b42 | |
| 43 | 101010 | 1 | 000 | 001111 | b42 → БП b15 |
| 44 | 101011 | 0 | 011010 | b43 → b44 | |
| 45 | 101100 | 0 | 011011 | b44 → b45 | |
| 46 | 101101 | 1 | 000 | 001111 | b45 → БП b15 |
| 47 | 101110 | 1 | 001 | 110000 | b46 → |
| 48 | 101111 | 0 | 100010 | b47 → кінець | |
| 49 | 110000 | 0 | 100000 | b48 → b49 | |
| 50 | 100001 | 0 | 100001 | b49 → кінець | |
Табл. 3.6 – Таблиця кодів станів автомата з природною адресацією команд
| № п/п | Стан | Код |
| 1 | b0 | 000000 |
| 2 | b1 | 000001 |
| 3 | b2 | 000010 |
| 4 | b3 | 000011 |
| 5 | b4 | 000100 |
| 6 | b5 | 000101 |
| 7 | b6 | 000110 |
| 8 | b7 | 000111 |
| 9 | b8 | 001000 |
| 10 | b9 | 001001 |
| 11 | b10 | 001010 |
| 12 | b11 | 001011 |
| 13 | b12 | 001100 |
| 14 | b13 | 001101 |
| 15 | b14 | 001110 |
| 16 | b15 | 001111 |
| 17 | b16 | 010000 |
| 18 | b17 | 010001 |
| 19 | b18 | 010010 |
| 20 | b19 | 010011 |
| 21 | b20 | 010100 |
| 22 | b21 | 010101 |
| 23 | b22 | 010110 |
| 24 | b23 | 010111 |
| 25 | b24 | 011000 |
| 26 | b25 | 011001 |
| 27 | b26 | 011010 |
| 28 | b27 | 011011 |
| 29 | b28 | 011100 |
| 30 | b29 | 011101 |
| 31 | b30 | 011110 |
| 32 | b31 | 011111 |
| 33 | b32 | 100000 |
| 34 | b33 | 100001 |
| 35 | b34 | 100010 |
| 36 | b35 | 100011 |
| 37 | b36 | 100100 |
| 38 | b37 | 100101 |
| 39 | b38 | 100110 |
| 40 | b39 | 100111 |
| 41 | b40 | 101000 |
| 42 | b41 | 101001 |
| 43 | b42 | 101010 |
| 44 | b43 | 101011 |
| 45 | b44 | 101100 |
| 46 | b45 | 101101 |
| 47 | b46 | 101110 |
| 48 | b47 | 101111 |
| 49 | b48 | 110000 |
| 50 | b49 | 110001 |
Табл. 3.7 – Таблиця вхідних сигналів автомата з природною адресацією команд
| № п/п | Вхідний стан | Код |
| 1 | Х0 | 000 |
| 2 | Х1 | 001 |
| 3 | Х2 | 010 |
| 4 | Х3 | 011 |
| 5 | X4 | 100 |
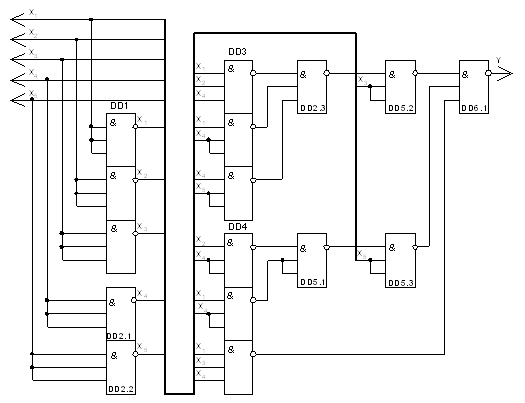
Рівняння вихідних сигналів та їх синтез у заданий базис:
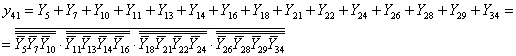
Синтез мультиплексора
Табл. 3.8 – Карта Карно до мультиплексора
|
| 00 | 01 | 11 | 10 |
| 0 1 | x0 | x1 | x3 | x2 |
| x4 | * | * | * |
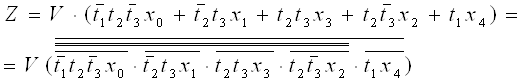
Похожие работы
... льш прості операції які називаються мікроопераціями тобто кожна операція – це визначена послідовність мікрооперацій. Існують два основні типи керуючих автоматів 1. Керуючий автомат з жорсткою чи схемною логікою. Для кожної операції будується набір комбінаційних схем які в потрібних тактах збуджують відповідні керуючі сигнали. Іншими словами ...
... Таблиця переходів автомата 2.2.3. Кодування станів 2.2.5. Функції збудження тригерів та вихідних сигналів Закінчення Список використаної літератури 1 Введення Метою курсового проекту по дисципліні "Прикладна теорія цифрових автоматів" є закріплення основних теоретичних знань і практичних навичок у ході самостійної роботи. У ході роботи необхідно :1. спроектувати керуючий автомат Милі по ...
. 2002 Керівник: Ніколенко А.О. Прийняв до виконання: Ткаченко І.О. Зміст Завдання на розробку Зміст Синтез комбінаційної схеми Розрахування значень Мінімізація БФ Комбінаційна схема Проектування автоматів Вибір завдання Автомат Мура Автомат Мілі Заключення Перелік літератури 1 Синтез комбінаційної схеми 1.1 Визначення значень БФ Булева функція 5 змінних ...
... функції менше, ніж МКНФ, обираємо для реалізації МДНФ функції. Реалізацію будемо проводити згідно з заданим базисом 2ЧИ-НІ. Застосуємо до обраної форми факторний алгоритм та одержимо скобкову форму для заданої функції: у = у = у = 2. Вибір блоків та структури ГСА Граф-схеми алгоритмів обираються кожним студентом індивідуально. Граф-схема складається з трьох блоків E, F, G і вершин ...
0 комментариев