Навигация
Математичні моделі потоків заявок та процесів обслуговування у мережах зв'язку
2. Математичні моделі потоків заявок та процесів обслуговування у мережах зв'язку
мережа зв'язок математичний заявка
Окрім структури, математична модель мережі зв'язку повинна описувати потоки заявок та їх обслуговування у мережі. Ці процеси мають стохастичний характер. Розглянемо їх математичні моделі, що будуються на основі теорії випадкових процесів та теорії масового обслуговування.
Основні характеристики випадкових потоків заявок. Випадковий потік заявок розглядається як послідовність випадкових величин, яка може бути задана різними способами, зокрема у вигляді:
- послідовності випадкових моментів часу появи заявки ![]() ;
;
-послідовністю випадкових інтервалів часу між заявками
![]() ;
;
-послідовністю випадкових чисел ![]() , що визначають кількість заявок на заданих інтервалах часу
, що визначають кількість заявок на заданих інтервалах часу ![]() .
.
При перших двох способах задання потік заявок розглядається як випадковий точковий процес, а при третьому - як випадковий цілочисельний процес ![]() із початковим значенням
із початковим значенням ![]() .
.
Імовірнісний опис таких випадкових процесів використовує такі характеристики: закон розподілу або відповідну щільність ймовірності моментів часу появи заявок чи інтервалів часу між заявками, а також закон розподілу кількості заявок на заданих інтервалах часу.
В залежності від властивостей цих характеристик розглядаються різні типи потоку заявок: ординарний та неординарний, стаціонарний та нестаціонарний, без післядії та з післядією.
Зокрема, для стаціонарного потоку закон розподілу кількості заявок не залежить від початкового моменту часу. Ординарність означає неможливість одночасного надходження двох і більше заявок. Відсутність післядії означає взаємну незалежність кількостей появи заявок на інтервалах часу, що не перекриваються.
Кількісний опис заявок використовує три основні характеристики:
- провідну функцію потоку, що являє собою середню кількість заявок за інтервал часу ![]() ;
;
- інтенсивність потоку, що являє собою середню кількість заявок за одиницю часу;
- параметр потоку, що визначається імовірністю появи хоча б однієї завки на малому інтервалі часу ![]() (
(![]() ).
).
Однорідний стаціонарний потік без післядії називається найпростішим потоком. Інтервали часу між заявками в ньому є незалежними випадковими величинами з показниковим розподілом, для якого щільність ймовірності має вигляд
![]() , (5)
, (5)
де ![]() - параметр потоку.
- параметр потоку.
Найпростіший потік заявок називається також пуасоновим, бо кількість заявок ![]() на інтервалі часу тривалістю
на інтервалі часу тривалістю ![]() розподілена за законом Пуасона
розподілена за законом Пуасона
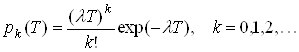 (6)
(6)
При застосуванні до найпростішого потоку з параметром ![]() операції проріджування (вилучення із нього частини заявок), одержується рекурентний потік з відновленням. Якщо при цьому
операції проріджування (вилучення із нього частини заявок), одержується рекурентний потік з відновленням. Якщо при цьому ![]() заявок підряд втрачається, а залишається тільки кожна
заявок підряд втрачається, а залишається тільки кожна ![]() , то проріджений потік має параметр
, то проріджений потік має параметр ![]() та щільність ймовірності для інтервалів часу між заявками
та щільність ймовірності для інтервалів часу між заявками
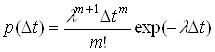 (7)
(7)
Такий розподіл носить назву розподілу Ерланга ![]() -го порядку, а відповідні потоки називаються ерлангівськими. За допомогою розподілу Ерланга є можливість опису широкого класу потоків - від найпростішого (при
-го порядку, а відповідні потоки називаються ерлангівськими. За допомогою розподілу Ерланга є можливість опису широкого класу потоків - від найпростішого (при ![]() ) до детермінованого з постійною тривалістю інтервалів між заявками (при
) до детермінованого з постійною тривалістю інтервалів між заявками (при ![]() ).
).
Основні характеристики систем масового обслуговування з втратами. Дисципліною обслуговування з явними втратами називається така, при якій заявка, що надходить у систему, отримавши відмову в обслуговуванні, покидає систему.
При обслуговуванні потоку заявок системою кожна з них займає обслуговуючий прилад (канал зв’язку) на деякий інтервал часу. Для систем розподілу інформації як одного із класів систем масового обслуговування важливе значення має сумарний час зайняття каналів при обслуговуванні заявок.
Тому дослідження цих систем проводиться на основі сумарного часу обслуговування заявок, що називається навантаженням. Як правило, розрізняють навантаження, що обслуговується, що надходить і що втрачається.
Навантаження ![]() , що обслуговується системою за інтервал часу
, що обслуговується системою за інтервал часу ![]() являє собою сумарний час зайняття всіх каналів системи обслуговування потоку заявок, які надходять на її входи за цей інтервал часу
являє собою сумарний час зайняття всіх каналів системи обслуговування потоку заявок, які надходять на її входи за цей інтервал часу
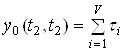 , (8)
, (8)
де ![]() - сума інтервалів часу, протягом яких
- сума інтервалів часу, протягом яких ![]() - й канал був зайнятий обслуговуванням на інтервалі часу
- й канал був зайнятий обслуговуванням на інтервалі часу ![]() ;
; ![]() - кількість каналів обслуговування.
- кількість каналів обслуговування.
Під інтенсивністю навантаження розуміється навантаження за одиницю часу. Інтенсивність навантаження, що обслуговується, при заданій якості обслуговування характеризує пропускну здатність системи розподілу інформації.
Кількісно вона оцінюється величиною середньої пропускної здатності або середнього часу використання одного каналу
![]() (9)
(9)
Під навантаженням ![]() , що надходить у систему за інтервал часу
, що надходить у систему за інтервал часу ![]() , розуміється таке навантаження, яке може бути обслужене нею за цей інтервал в умовах негайного надання обслуговування кожній заявці, яка надходить.
, розуміється таке навантаження, яке може бути обслужене нею за цей інтервал в умовах негайного надання обслуговування кожній заявці, яка надходить.
Навантаження ![]() , що втрачається системою протягом інтервалу часу
, що втрачається системою протягом інтервалу часу ![]() , являє собою різницю між навантаженнями
, являє собою різницю між навантаженнями ![]() та
та ![]() .
.
Для кількісної оцінки якості обслуговування з втратами на інтервалі ![]() використовуються такі характеристики: втрати за часом, як частина часу на цьому інтервалі, протягом якого всі доступні канали системи зайняті обслуговуванням; втрати за заявками, як відношення числа втрачених за цей відрізок часу заявок до загальної кількості заявок, що надійшли до системи; втрати за навантаженням, як відношення навантаження, що втрачається, до навантаження, що надходить за той же інтервал часу.
використовуються такі характеристики: втрати за часом, як частина часу на цьому інтервалі, протягом якого всі доступні канали системи зайняті обслуговуванням; втрати за заявками, як відношення числа втрачених за цей відрізок часу заявок до загальної кількості заявок, що надійшли до системи; втрати за навантаженням, як відношення навантаження, що втрачається, до навантаження, що надходить за той же інтервал часу.
Стани системи обслуговування ![]() визначаються кількістю заявок, які знаходяться у системі на обслуговуванні. Для дисципліни обслуговування з втратами ця кількість збігається з кількістю зайнятих каналів системи.
визначаються кількістю заявок, які знаходяться у системі на обслуговуванні. Для дисципліни обслуговування з втратами ця кількість збігається з кількістю зайнятих каналів системи.
При цьому процес обслуговування системою заявок ![]() може приймати різні значення в залежності від стану системи: стан
може приймати різні значення в залежності від стану системи: стан ![]() , коли вільні всі
, коли вільні всі ![]() каналів; стан
каналів; стан ![]() , коли зайнятий один канал, а інші вільні; стан
, коли зайнятий один канал, а інші вільні; стан ![]() , коли зайнято
, коли зайнято ![]() каналів, а інші вільні;
каналів, а інші вільні; ![]() , коли зайняті всі
, коли зайняті всі ![]() каналів.
каналів.
В разі найпростішого потоку заявок з параметром ![]() і показниковим розподілом тривалості обслуговування з функцією розподілу
і показниковим розподілом тривалості обслуговування з функцією розподілу ![]() фінальні ймовірності вказаних станів системи
фінальні ймовірності вказаних станів системи ![]() визначаються першою формулою Ерланга
визначаються першою формулою Ерланга
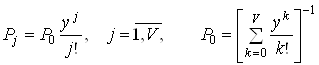 , (10)
, (10)
де ![]() - інтенсивність навантаження, що надходить.
- інтенсивність навантаження, що надходить.
Динаміка станів системи обслуговування з втратами для найпростішого або примітивного потоку та показниково розподіленої тривалості обслуговування описується дискретними марківськими процесами народження та загибелі.
При їх імітаційному моделюванні на ЕОМ використовуються ланцюги Маркова із ![]() -м станом
-м станом ![]() , що створюються на інтервалі часу спостереження у вигляді послідовності відліків у моменти часу
, що створюються на інтервалі часу спостереження у вигляді послідовності відліків у моменти часу ![]() . У цих ланцюгах розглядаються переходи між станами через одиничні моменти часу.
. У цих ланцюгах розглядаються переходи між станами через одиничні моменти часу.
Аналогічно на основі теорії масового обслуговування будуються математичні моделі складніших систем обслуговування з очікуванням. Дисципліною обслуговування з очікуванням називається така, при якій заявка, що надходить у систему за відсутністю вільних обслуговуючих приладів (каналів), не втрачається, а ставиться до черги, очікуючи звільнення будь якого з них.
Наряду із показниками завантаження каналів система обслуговування з очікуванням додатково описується такими характеристиками: ймовірність умовних втрат за часом, яка визначається середньою часткою часу, коли всі канали зайняті обслуговуванням; ймовірність затримки (очікування початку обслуговування) заявки понад заданий час; середній час очікування обслуговування; ймовірність того, що довжина черги перевищить задану величину; середня довжина черги.
Процес обслуговування описується випадковим процесом, що приймає дикретні значення і визначається кількістю заявок, які присутні у системі обслуговування.
При цьому характерні такі стани системи: стан ![]() , коли вільні всі
, коли вільні всі ![]() каналів; стан
каналів; стан ![]() , коли зайнятий один канал, а інші вільні; стан
, коли зайнятий один канал, а інші вільні; стан ![]() , коли зайнято
, коли зайнято ![]() каналів, а інші вільні; стан
каналів, а інші вільні; стан ![]() , коли зайняті всі
, коли зайняті всі ![]() каналів; стан
каналів; стан ![]() , коли зайняті всі
, коли зайняті всі ![]() каналів та одна заявка стоїть у черзі; стан
каналів та одна заявка стоїть у черзі; стан ![]() , коли зайняті всі
, коли зайняті всі ![]() каналів та
каналів та ![]() заявок стоїть у черзі.
заявок стоїть у черзі.
Довжина черги буде скінченною, якщо інтенсивність навантаження, що надходить, буде меншою за кількість каналів обслуговування у системі. Динаміка станів системи обслуговування з чергами описується дикретними марківськими процесами, зокрема ланцюгами Маркова.
Похожие работы
... зноманітними типами транспортних засобів з урахуванням обмеження на обсяг робот, що можуть виконати транспортні засоби. РОЗДІЛ 3 МАТЕМАТИЧНА МОДЕЛЬ ТРАНСПОРТНОЇ СИСТЕМИ ПІДПРИЄМСТВА 3.1 Структура моделі У якості структурної моделі транспортної системи підприємства можна запропонувати схему, що складається з трьох рівнів. Необхідно відзначити, що з метою деякого спрощення задачі розгляда ...
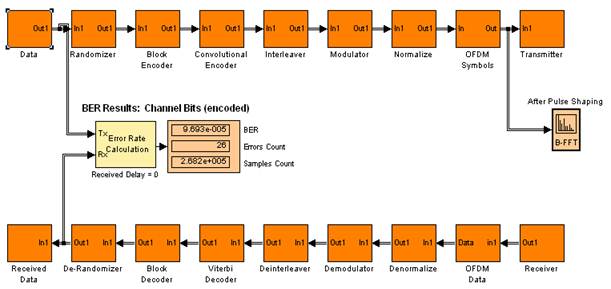
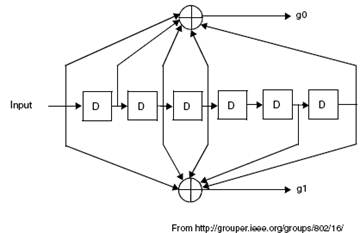
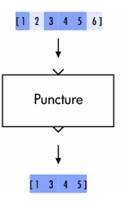
... XOR між отриманою послідовністю після селектора та псевдовипадковою послідовністю, в результаті чого отримується початковий сигнал. Рис.1.21. De-Randomizer. 3.Теоретичний огляд розрахунку покриття WiMax Розрахунок покриття WiMax – досить неоднозначний процес, що залежить від великої кількості параметрів середовища передачі та тих, що закладені в будову системи WiMax. Розрізняють дві ...
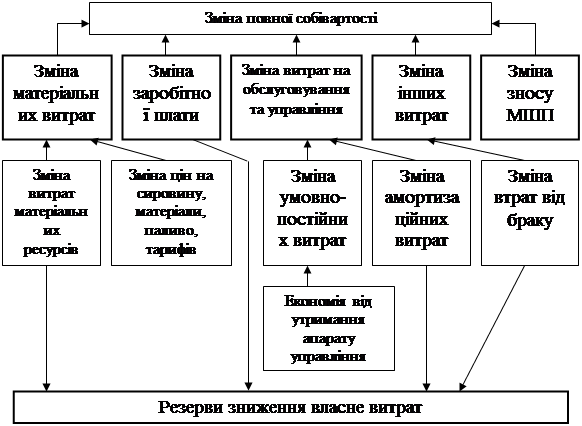
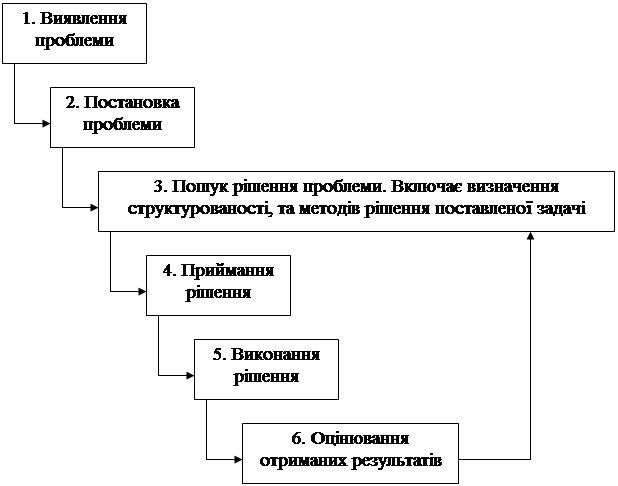
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...
... Генерування сигналу 5. Модулятор моделювання сигналу-носія повідомленням 3. Математичний опис сигналів при моделюванні систем зв’язку При моделюванні систем зв’язку важливим є опис реальних сигналів і завад їх математичними моделями, що базуються на основних положеннях теорії сигналів. В системах зв'язку зустрічаються різного виду детерміновані та ...

0 комментариев