И т.д. Таким образом, наше предположение верно для всех целых чисел, из которых состоит данная прогрессия

5 и т.д. Таким образом, наше предположение верно для всех целых чисел, из которых состоит данная прогрессия.

Тот факт, что математическая индукция начинается с некоторого предположения (или гипотезы), сближает ее с индуктивными рассуждениями, но, так как предположение подкрепляется доказательством, основанным на переходе от an к an+1, это придает ей доказательный характер.

Обобщающая индукция

Кроме полной и математической индукции, которые приводят к достоверным заключениям, все остальные формы индукции лишь наводят на истину, и потому их результаты имеют лишь проблематический (вероятностный) характер. Это иногда служит основанием для недооценки их роли в научном познании. Между тем стоит лишь задуматься над вопросом, откуда берутся общие посылки для дедуктивных умозаключений, как сразу же вспоминают о движении познания от частного к общему, а это и есть индукция в общепринятом смысле слова.

В традиционной логике именно подобной индукции противопоставлялась дедукция, как переход от знания общего к частному. Хотя с современной точки зрения такое противопоставление, как мы видели, оказывается несостоятельным, тем не менее оно верно подмечает различие между типичными индуктивными обобщениями и дедуктивными умозаключениями. В этом смысле даже полная и математическая индукции могут с известными оговорками рассматриваться как особые случаи обобщающей индукции, поскольку ход рассуждения в них является типично индуктивным, основанным на исследовании некоторых частных случаев и переносе открытого в результате этого знания на весь их класс в целом. Однако к типичным видам индуктивного обобщения относят различные формы неполной индукции, когда заключение имеет не достоверный, а лишь правдоподобный (вероятностный) характер. При этом степень вероятности заключения зависит от глубины и тщательности исследования тех конкретных случаев, на которые опирается индуктивное обобщение. Соответственно можно выделить несколько видов индуктивного обобщения.

Индукция через перечисление случаев

Более полно и точно это понятие может быть выражено так: индукция посредством перечисления частных случаев, подтверждающих обобщение, пока не встретится случай, противоречащий ему. По-видимому, это один из древнейших способов рассуждений, который часто используется в повседневной практике. При этом систематического анализа случаев, подтверждающих предположение общего характера, не проводится. Такие индуктивные обобщения основываются на выделении поверхностных, чаще всего бросающихся в глаза свойств вещей и явлений, вследствие чего они в наибольшей степени подвержены риску опровержения. Традиционный и поучительный пример такого обобщения представляет собой индуктивное обобщение "Все лебеди белые". По-видимому, оно было получено на основе простого перечисления случаев наблюдения окраски лебедей, которые встречались в Европе. Обнаружение черных лебедей в Австралии сразу же опровергло прежнее обобщение.

Несмотря на то что подобный вид индуктивного обобщения подвержен риску опровержения, тем не менее он широко используется в повседневных рассуждениях, почему нередко его называют популярной индукцией. Чтобы повысить степень надежности обобщения, необходимо, во-первых, из открытых в ходе наблюдения или исследования общих свойств выбрать свойства наиболее важные и существенные, во-вторых, постараться найти определенную связь между вновь открытыми и уже известными свойствами. Ясно, что если бы была установлена связь между цветом лебедей и более важными их анатомо-физиологическими свойствами, влиянием на окраску климатических и иных условий, то индуктивное обобщение было бы более правдоподобным. Ошибки подобного рода, допускаемые в популярной индукции, квалифицируются как поспешные обобщения.

Энумеративная индукция

Чтобы повысить вероятность индуктивного обобщения, основанного на перечислении частных случаев, их располагают в определенной последовательности начиная с простейших и постепенно восходя к исследованию всех остальных. Такой прием индукции Р. Декарт сравнивал с цепью, в которой мы можем ясно различать связь между отдельными ее звеньями, но если она длинная, то не можем охватить ее взглядом целиком. По сути дела такой же подход используется в математической индукции, где демонстрируется переход от одного элемента числового ряда к другому, и на этой основе раскрывается закономерный характер построения тех или иных числовых рядов, например арифметической прогрессии. Сам Декарт применил этот способ для систематического исследования свойств алгебраических кривых в аналитической геометрии. Такой же строгой последовательности по возможности следует придерживаться при исследовании не только математических, но и других научных объектов. Однако энумеративная индукция (лат. enumeratio – перечисление, перечень) представляет собой лишь первый шаг на пути к выдвижению правдоподобного обобщения. Дальнейший шаг состоит в отборе и исследовании более надежных случаев и исключении менее надежных.

Элиминативная индукция

Как показывает само название (лат. eleminatio – исключение, удаление), такая индукция основывается на исключении случаев, в которых свойства исследуемых предметов и явлений не согласуются с предполагаемым общим свойством или закономерностью. Такой метод, по сути дела, широко применялся уже Ф. Бэконом, а впоследствии был систематизирован Д.С. Миллем при анализе простейших причинных связей между явлениями. Очевидно, что общая причина, которая определяет существование всех рассматриваемых явлений, должна присутствовать во всех из них. Поэтому путем проверки значительного числа случаев, которые отличаются друг от друга, следует исключить все случаи, где общая причина отсутствует. Таким путем приходят к выявлению предполагаемой причины, которую Милль называл основой существования действия или следствия. Подробнее это будет изложено в дальнейшем. Здесь же достаточно отметить, что путем элиминации (исключения) случаев, где общее свойство, причина или закономерность отсутствуют, находят общее свойство, или закономерность, или причину, где они действительно присутствуют. Такой способ отрицательного движения к истине является весьма обычным во всех случаях, когда сравнивают различные предположения, гипотезы или судебные версии, оценивая их вероятность на основе исключения опровергающих случаев.

Индукция и научное познание

Использование различных форм и методов индукции характерно прежде всего для опытных и фактуальных на ук, имеющих дело с явлениями природы, социально-экономическими и гуманитарными процессами, а они как раз и составляют преобладающую часть научного знания. Формальные науки, к которым относят математику, логику и родственные им дисциплины, могут развиваться относительно самостоятельно, не обращаясь непосредственно к опыту, используя дедукцию для получения новых истин. Но и в математике роль индукции и аналогии, как показали исследования таких известных ученых, как А. Пуанкаре, Ш. Адамар, Д. Пойа и другие, достаточно ощутима. Тем не менее в ней всякое новое открытие принимается только тогда, когда оно доказывается, т.е. приводится в логическую связь с другими истинами путем логической дедукции. Вот почему дедуктивная логика находит наибольшее применение именно в математике, где все теории стремятся представить в аксиоматически-дедуктивной форме.

Индукция и подтверждение гипотез

В научном познании индукция играет двоякую роль:

1) путем обобщения частных случаев она помогает создавать новые научные гипотезы и тем самым играет эвристическую роль. Без этого невозможен был бы рост знания и прогресс науки;

2) поскольку индуктивные гипотезы, как и любые предположения имеют проблематический характер, они нуждаются в тщательной логической и эмпирической проверке.

Логическая проверка гипотез сводится к выведению из них таких следствий, которые допускают эмпирическую проверку, т.е. сопоставление полученных результатов с данными наблюдений и специально поставленных экспериментов.

Многие научные гипотезы формулируются с помощью абстрактных понятий и суждений, и поэтому не могут быть непосредственно проверены на опыте, в связи с чем и возникает необходимость в обращении к косвенным методам их проверки. В этих целях из них выводятся определенные следствия, которые допускают эмпирическую интерпретацию, т.е. могут быть выражены с помощью терминов наблюдения. Посредством такой процедуры установления соответствия между теоретическими и эмпирическими понятиями становится возможной проверка теоретических гипотез.

В качестве примера сошлемся хотя бы на такую исходную гипотезу, как свойство тел сохранять состояние покоя или равномерного прямолинейного движения, которое было названо инерцией и впоследствии стало законом в классической механике. Очевидно, что ни в каком реальном эксперименте нельзя ее проверить непосредственно, так как невозможно наблюдать движение тел, на которые не оказывали бы воздействия различные внешние силы (трения, сопротивления воздуха и т.п.). В связи с этим в данном случае прибегают к различным косвенным методам проверки, наблюдая, например, как изменяется скорость движения при уменьшении сил трения и других внешних сил. Еще более характерны в этом отношении гипотезы, объясняющие поведение макротел с помощью внутреннего механизма их строения, например, как это делает молекулярно-кинетическая гипотеза, когда объясняет расширение тел при нагревании, изменение объема газа – с увеличением или уменьшением его давления и тому подобное – с помощью предположения о существовании в веществе беспорядочно движущихся частиц (молекул и атомов). Наблюдать такие частицы непосредственно мы не в состоянии, поэтому проверить подобные гипотезы можно по тем эмпирически наблюдаемым следствиям, которые из них вытекают.

Когда мы располагаем эмпирически проверяемой гипотезой, то в состоянии сопоставить ее с теми фактами, событиями и явлениями, которые релевантны к ней, т.е. могут подтвердить ее или опровергнуть. Символически такую гипотезу можно представить в виде формулы:

Р (Н/Е) = с,

где Р – вероятность;

Н – гипотеза;

Е – эмпирические свидетельства гипотезы;

с – степень подтверждения или индуктивной вероятности гипотезы.

Вероятность индуктивного обобщения или эмпирической гипотезы в существенной мере определяется теми свидетельствами (фактами, результатами наблюдений и экспериментов, показаниями очевидцев и т.п.), которые к ним относятся. Как уже отмечалось выше, эта степень подтверждения гипотезы изменяется вместе с изменением подтверждаемых ее данных. В принципе, чем больше количество подтверждающих гипотезу свидетельств, тем выше ее вероятность. Но если эти свидетельства мало отличаются друг от друга, то они ненамного усиливают нашу веру в гипотезу. Другое дело, если подтверждающие случаи гипотезы заметно разнятся друг от друга. Тогда наша вера в нее заметно усиливается.

Относительно количественного определения степени подтверждения гипотезы мнения специалистов, как мы отмечали, заметно различаются, начиная от допущения выражения этой степени числом и кончая отрицанием возможности ее оценки даже в сравнительных терминах.

Существует асимметрия между подтверждением и опровержением гипотез. Она заключается в том, что никакое подтверждение нельзя считать окончательным и абсолютным. Сколько бы случаев не подтверждали гипотезу, в принципе всегда может со временем появиться случай, который в состоянии будет ее опровергнуть. Опровержение с чисто логической точки зрения считается окончательным: всякий противоречащий случай опровергает гипотезу. Такая асимметрия ясно видна из сравнения схем подтверждения и опровержения любых высказываний, а не только гипотез:

А → В А → В

В ¬ В

А вероятно ¬ А (ложно)

Как мы уже знаем, из подтверждения следствия можно сделать заключение лишь об увеличении степени вероятности заключения, причем эта степень возрастает незначительно, если полученное следствие мало отличается от предыдущих, но возрастает заметно, когда следствие будет значительно отличаться от предыдущих. Эта схема приведена слева. На правой схеме представлено опровержение, которое совершается по схеме дедуктивной логики modus tollens, т.е. из ложности следствия заключают о ложности основания. Именно такой характер опровержения используется некоторыми современными философами для того, чтобы выбрать его в качестве критерия проверки научных гипотез.

Однако, как показывает реальная практика научного исследования, и подтверждение, и опровержение гипотез являются необходимыми для их обоснования. Подтверждение необходимо хотя бы для того, чтобы убедиться, что выдвигаемая гипотеза основывается на реальных фактах, а не является чисто умозрительным построением. Опровержение дает возможность отсеивать неправдоподобные гипотезы и тем самым сужает круг поиска подлинной гипотезы. К тому же не следует забывать, что в современной науке процесс опровержения гипотез не носит такой простой характер, как он представляется в логике. Действительно, новые гипотезы могут войти в теоретическую систему только тогда, когда они будут связаны с другими гипотезами логическими отношениями, а опровержение системы гипотез представляет более серьезную проблему, чем опровержение отдельной, изолированной гипотезы. С помощью вспомогательных гипотез od hoc, т.е. придуманных для данного случая, всегда можно спасти систему от опровержения.

Гипотетико-дедуктивный метод

Во многих рассуждениях в науке индукция часто сопровождается дедукцией. В эмпирических науках индукция используется для обобщения данных, результатов наблюдения или экспериментального исследования. Заключения, полученные таким способом, представляют собой гипотезы, правильность которых в дальнейшем проверяется путем выведения логических следствий из них. После того как ученые постепенно пришли к осознанию той мысли, что индуктивная логика не может считаться безошибочным средством для открытия новых научных истин, они все больше стали обращать внимание на гипотетико-дедуктивный метод исследования. Но этот метод является не столько методом открытия, сколько способом построения и обоснования научного знания, поскольку он показывает, каким именно путем можно прийти к новой научной гипотезе. Ведь в формировании гипотезы участвует и догадка, и индукция, и воображение, и индуктивное обобщение, не говоря уже об опыте, квалификации и таланте ученого. Все эти факторы трудно или почти не поддаются логическому анализу, в связи с чем некоторые философы относят исследование таких вопросов к области психологии творчества, а задачу логики видят лишь в логической проверке гипотез, которая сводится прежде всего к дедукции (выводу) следствий из гипотез. Индукция же здесь рассматривается не столько как способ формирования новых гипотез, сколько как метод их проверки с помощью эмпирических свидетельств и сопоставления их со следствиями, выведенными из гипотез.

Истоки гипотетико-дедуктивного метода восходят к античной философии и риторике. Известно, что Сократ и Платон в своих диалогах выводили следствия из мнений и предположений, высказанных их оппонентами. Сопоставляя эти предположения с реальными фактами и твердо установленными истинами, Сократ и Платон опровергали ошибочные мнения и ходячие представления. Таким образом, проверка мнений и предположений, представляющих собой гипотезы, осуществлялась в диалогах с помощью гипотетико-дедуктивного метода, который играл важную роль в процессе убеждения и аргументации. Не случайно в современной литературе утверждают, что основанный Сократом метод диалога (диалектики) является одной из форм гипотетико-дедуктивного способа рассуждения. Правда, такой взгляд характеризует лишь некоторые внешние, формальные особенности реального диалога, в котором существенную роль играет прежде всего постановка вопросов. Ответы же выступают в виде гипотез, мнений и предложений.

По-настоящему гипотетико-дедуктивные рассуждения начали применяться впервые в точном естествознании после того, как возник экспериментальный метод исследования и связанные с ним количественные методы. Наиболее широко этот метод использовался основателями классической механики Галилеем и Ньютоном.

О том, как применялся этот метод в конкретном исследовании, свидетельствуют "Беседы и математические доказательства ..." Галилея. В них он подробно излагает способ аргументации, с помощью которого пришел к открытию и обоснованию своего важнейшего открытия – закона постоянства ускорения падающих тел. Сначала Галилей, как и его предшественники, придерживался гипотезы, что скорость падения тела (v) пропорциональна (к) пройденному пути (s), т.е. v = к   s. Однако эксперимент не подтверждал ее, поэтому он принял другую гипотезу: скорость пропорциональна времени падения (t), т.е. v = g   t, где g обозначает ускорение силы тяжести.

Из этой гипотезы чисто математически можно вывести заключение, что пройденный телом путь при падении пропорционален квадрату времени падения:

Наконец, из полученного заключения можно вывести бесчисленное множество частных следствий, если рассматривать пути, пройденные телом за 1, 2, 3 секунды:

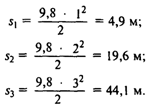
Во всех этих формулах s обозначает путь, t – время, g = 9,8 м/с² – ускорение свободнопадающего тела.

Полученные результаты из исследования гипотезы можно проверить непосредственными измерениями, и тем самым подтвердить не только окончательное, но и промежуточные следствия из нее.

Построение своей теории Ньютон начинает с определения ее основных понятий и формулирования трех ее основных законов. Из них выводятся множество следствий, которые можно рассматривать как производные законы. В частности, из второго закона механики легко выводится закон свободного падения тел, открытый до этого Галилеем.

После Ньютона роль гипотетико-дедуктивного метода в построении и обосновании теорий опытных наук стала такой же общепризнанной, как и аксиоматического метода – для математических наук.