Навигация
Формирование возможных значений случайных величин с заданным законом распределения
87889
знаков
14
таблиц
8
изображений
1.1 Формирование возможных значений случайных величин с заданным законом распределения
Для формирования возможных значений случайных величин с заданным законом распределения используются случайные величины, равномерно распределенные на интервале [0;1]. Методика получения случайных величин с заданным законом распределения основана на следующем. Пусть случайная величина 
распределена в соответствии с законом
(1.1)
где 
- плотность распределения случайной величины 
.
Найдем распределение случайной величины 
где функция 
задана соотношением (1.1). По определению закон распределения 
случайной величины 
есть
(1.2)
причем 
Отсюда следует, что случайная величина 
равномерно распределена в интервале [0;1]. Используя (1.2), запишем
(1.3)
Тогда, если 
- последовательность значений случайной величины 
, равномерно распределенной в [0;1], то, решая уравнение (1.3), получим соответствующую последовательность 
случайных чисел, распределенных по закону (1.1), причем
(1.4)
Рассмотрим примеры. Пусть требуется получить случайные числа 
с показательным законом распределения
(1.5)
Используя (1.4), получим
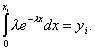(1.6)
где 
- случайная величина с равномерным распределением на интервале [0;1]. Отсюда
(1.7)
Тогда
(1.8)
Пусть теперь нужно получить случайные величины, распределенные по релеевскому закону с плотностью
(1.9)
Имеем
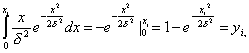(1.10)
Откуда
(1.11)
Нужно иметь в виду, что в большинстве случаев уравнение (1.3) невозможно решать точно (например, если требуется получить числа, распределенные по нормальному закону). В связи с этим на практике широко используют приближенные методы получения чисел, распределенных в соответствии с заданным законом. Рассмотрим один из таких алгоритмов.
1.2 Метод НейманаПусть 
- плотность распределения случайной величины, заданной на конечном интервале 
В предположении, что 
ограничена сверху, приведем ее значения к интервалу 
, введя
(1.12)
При этом график 
окажется вписанным в прямоугольник с координатами (a;0), (a;1), (b;1), (b;0), (рис. 1.1).
 |
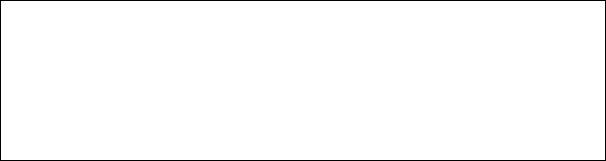Рис. 1.1 - График 
Выберем пару чисел 
и 
из равномерно распределенных в интервале 
последовательностей 
При этом пара чисел 
и 
определяет случайную точку 
в указанном прямоугольнике. Теперь в качестве случайных чисел с заданной плотностью 
будем принимать те 
, для которых 
Если же это неравенство не выполняется, то пара 
отбрасывается и формируется следующая.
Докажем, что закон распределения отобранных таким образом чисел 
соответствует распределению 
Для доказательства выберем интервал 
и введем области
и
(1.13)
Вычислим вероятность попадания не отброшенных точек в область 
Так как
(1.14)
а
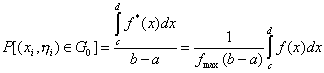(1.15)
и
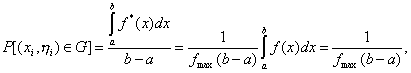(1.16)
то искомая вероятность
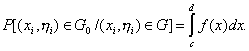(1.17)
полученная вероятность равна вероятности попадания случайной величины, распределенной в соответствии с 
на интервал 
откуда следует требуемое.
Одним из математических методов исследования стохастических сложных систем является теория массового обслуживания, занимающаяся анализом эффективности функционирования так называемых систем массового обслуживания. Работа любой такой системы заключается в обслуживании поступающего на нее потока требований, или заявок. Заявки поступают на систему одна за другой в некоторые, вообще говоря, случайные моменты времени. Обслуживание поступившей заявки продолжается какое-то время, после чего система освобождается для обслуживания очередной заявки. Каждая такая система может состоять из нескольких независимо функционирующих единиц, которые называют каналами обслуживания, или обслуживающими аппаратами. Примерами таких систем могут быть: телефонные станции, билетные кассы, аэродромы, вычислительные центры, радиолокационные станции и т. д. Типичной системой массового обслуживания является автоматизированная система управления производством.
Математический аппарат теории массового обслуживания позволяет оценить эффективность обслуживания системой заданного потока заявок в зависимости от характеристик этого потока, числа каналов системы и производительности каждого из каналов.
В качестве критерия эффективности системы обслуживания могут быть использованы различные величины и функции, например: вероятность обслуживания каждой из поступающих заявок, средняя доля обслуженных заявок, среднее время ожидания обслуживания, среднее время простоя каждого из каналов и системы в целом, закон распределения длины очереди, пропускная способность системы и т. д. Численное значение каждого из этих критериев в той или иной степени характеризует степень приспособленности системы к выполнению поставленной перед ней задачи — удовлетворение потока поступающих в систему требований.
Часто термин «пропускная способность» используется в следующем узком смысле: среднее число заявок, которое система может обслужить в единицу времени. Эффективность систем обслуживания может быть оценена также величиной относительной пропускной способности— средним отношением числа обслуженных заявок к числу поступивших.
В силу случайного характера моментов поступления заявок процесс их обслуживания представляет собой случайный процесс. Теория массового обслуживания позволяет получить математическое описание этого процесса, изучение которого дает возможность оценить пропускную способность системы и дать рекомендации по рациональной организации обслуживания.
Все системы массового обслуживания имеют вполне определенную структуру, схематически изображенную на рис. 1.2. В соответствии с рисунком в любой системе массового обслуживания будем различать следующие основные элементы: входящий поток, выходящий поток, собственно система обслуживания.
Поток требований, нуждающихся в обслуживании и поступающих в систему обслуживания, называется входящим. Поток требований, покидающих систему обслуживания, называется выходящим.
 |
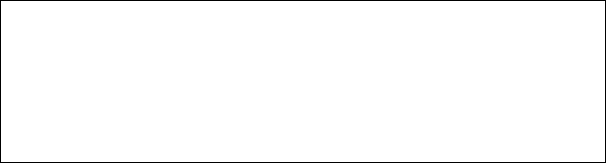Рис. 1.2 - Схема системы массового обслуживания
Совокупность обслуживающих аппаратов вместе с системой правил, устанавливающих организацию обслуживания, образуют систему обслуживания.
Похожие работы
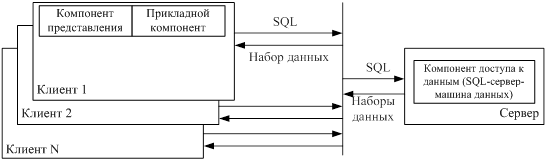
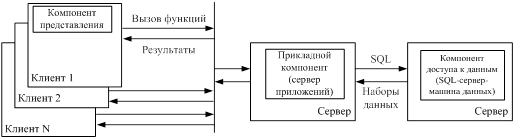
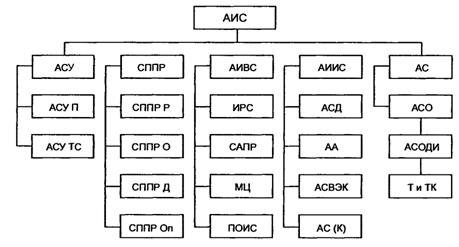
... называемые правила бизнеса) реализуются прикладными программами на клиентских установках (RDA-модель) или на сервере приложений (AS-модель). 2. Автоматизированные системы сбора, хранения и анализа информации Автоматизированные информационные системы (АИС) относятся к классу сложных систем, как правило, не столько в связи с большой физической размерностью, сколько в связи с многозначностью ...
... , практически, не используются. Проблема информатизации Минторга может быть решена путем создания Автоматизированной Информационной системы Министерства Торговли РФ (АИС МТ РФ) в соответствии с настоящим Техническим предложением. ГЛАВА 2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КОМПЛЕКСА ЗАДАЧ "СИСТЕМА ДОКУМЕНТООБОРОТА УЧЕРЕЖДЕНИЯ”. функции поиска и архивации 2.1. Постановка задачи и её спецификация ...
... стоящая за ним проблема информатизации общества. Внедрение современных информационных технологий в библиотечную деятельность, возможность предоставления информации из сколь угодно удаленных источников по каналам связи коренным образом меняют положение библиотек в стуктуре современного общества. Принципиально по-новому решаются проблемы своевременного получения научной информации, без чего сегодня ...
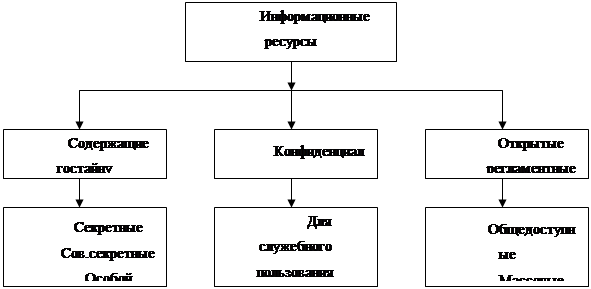
... равновесия между полнотой отчуждения и мерами защиты тайны должны выполняться тремя различными максимально независимыми друг от друга субъектами». Сформулированные принципы управления информационным производством могут эффективно действовать только в условиях жесткой технологической дисциплины, вынуждающей всех субъектов производства придерживаться этих принципов. Это возможно только тогда, ...
0 комментариев