Навигация
Моделювання оптимальної стратегії заміни обладнання за допомогою динамічного програмування
КУРСОВА РОБОТА
На тему
«Моделювання оптимальної стратегії заміни обладнання за допомогою динамічного програмування»
Суми – 2006
Вступ
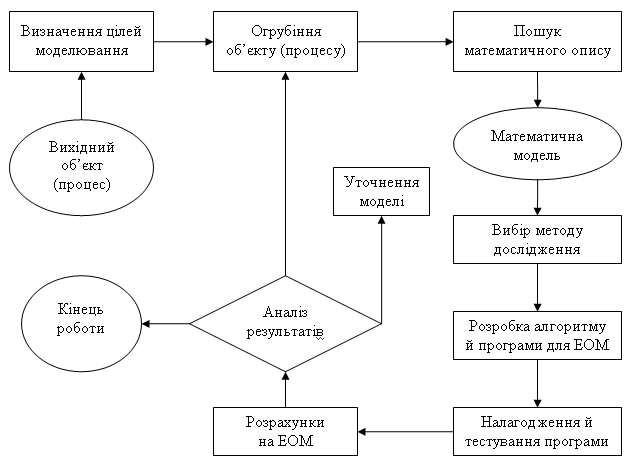
У наш час наука приділяє велику увагу питанням організацій й керування, це приводить до необхідності аналізу складних цілеспрямованих процесів під кутом зору їхньої структури й організації. Потреби практики викликали до життя спеціальні методи, які зручно поєднувати за назвою «дослідження операцій». Під цим терміном розуміється застосування математичних, кількісних методів для обґрунтування рішень у всіх областях цілеспрямованої людської діяльності.
Метою динамічного програмування є визначення найкращого способу дії при рішенні того або іншого завдання. Для побудови математичної моделі необхідно мати строге подання про мету функціонування досліджуваної системи й мати інформацію про обмеження, які визначають область припустимих значень. Мета й обмеження повинні бути представлені у вигляді функцій.
Практично всі методи динамічного програмування породжують алгоритми, які є ітераційними по своїй природі. Це має на увазі, що завдання вирішується послідовно (ітераціонно), коли на кожному кроці (ітерації) одержуємо рішення, що поступово сходяться до оптимального рішення.
Ітераційна природа алгоритмів звичайно приводить до об'ємних однотипних обчислень. У цьому й полягає причина того, що ці алгоритми розробляються, в основному, для реалізації за допомогою обчислювальної техніки.
Метою даної курсової роботи є знаходження оптимального плану заміни обладнання для максимізації прибутковості діяльності підприємства.
Об’єктом курсової роботи виступає будь-яке підприємство яке має устаткування та обладнання, що використовує для виготовлення продукції.
Предметом курсової роботи являється методи динамічного програмування.
1. Теоретичні відомості щодо динамічного програмування
Більшість методів дослідження операцій зв'язано в першу чергу із завданнями цілком певного змісту. Класичний апарат математики виявився малопридатним для рішення багатьох завдань оптимізації, що включають велике число змінних й/або обмежень у вигляді нерівностей. Безсумнівна привабливість ідеї розбивки завдання великої розмірності на підзадачі меншої розмірності, що включають усього по декількох змінних, і наступного рішення загального завдання вроздріб. Саме на цій ідеї заснований метод динамічного програмування.
Динамічне програмування (ДП) являє собою математичний метод, заслуга створення й розвитку якого належить насамперед Беллману. Метод можна використати для рішення досить широкого кола завдань, включаючи завдання розподілу ресурсів, заміни й керування запасами, завдання про завантаження. Характерним для динамічного програмування є підхід до рішення завдання по етапах, з кожним з яких асоційована одна керована змінна. Набір рекурентних обчислювальних процедур, що зв'язують різні етапи, забезпечує одержання припустимого оптимального рішення завдання в цілому при досягненні останнього етапу.
Походження назви динамічне програмування, імовірно, пов'язане з використанням методів ДП у завданнях прийняття рішень через фіксовані проміжки часу (наприклад, у завданнях керування запасами). Однак методи ДП успішно застосовуються також для рішення завдань, у яких фактор часу не враховується. Із цієї причини більше вдалим представляється термін багатоетапне програмування, що відбиває покроковий характер процесу рішення завдання.
Фундаментальним принципом, покладеним в основу теорії ДП, є принцип оптимальності. Власне кажучи, він визначає порядок поетапного рішення завдання, що допускає декомпозицію, (це більше прийнятний шлях, чим безпосереднє рішення завдання у вихідній постановці) за допомогою рекурентних обчислювальних процедур.
Динамічне програмування дозволяє здійснювати оптимальне планування керованих процесів. Під «керованими» розуміються процеси, на хід яких ми можемо в тім або іншому ступені впливати.
Нехай передбачається до здійснення деякий захід або серія заходів («операція»), що переслідує певну мету. Запитується: як потрібно організувати (спланувати) операцію для того, щоб вона була найбільш ефективною? Для того, щоб поставлене завдання придбало кількісний, математичний характер, необхідно ввести в розгляд деякий чисельний критерій W, яким ми будемо характеризувати якість, успішність, ефективність операції. Критерій ефективності в кожному конкретному випадки вибирається виходячи із цільової спрямованості операції й завдання дослідження (який елемент керування оптимізується й для чого).
Сформулюємо загальний принцип, що лежить в основі рішення всіх завдань динамічного програмування («принцип оптимальності»):
«Який би не був стан системи S перед черговим кроком, треба вибрати керування на цьому кроці так, щоб виграш на даному кроці плюс оптимальний виграш на всіх наступних кроках був максимальним».
Динамічне програмування – це поетапне планування багатокрокового процесу, при якому на кожному етапі оптимізується тільки один крок. Керування на кожному кроці повинне вибиратися з обліком всіх його наслідків у майбутньому.
При постановці завдань динамічного програмування варто керуватися наступними засадами:
– вибрати параметри (фазові координати), що характеризують стан S керованої системи перед кожним кроком;
– розчленувати операцію на етапи (кроки);
– з'ясувати набір крокових керувань xі для кожного кроку й обмеження, що накладають на них;
– визначити який виграш приносить на і-ом кроці керування xі, якщо перед цим система могла S, тобто записати «функцію виграшу»;
– визначити, як змінюється стан S системи S під впливом керування xі на і-ом кроці: воно переходить у новий стан;
– записати основне рекурентне рівняння динамічного програмування, що виражає умовний оптимальний виграш Wі(S) (починаючи з і-го кроку й до кінця) через уже відому функцію Wі+1 (S).
Цьому виграшу відповідає умовне оптимальне керування на і-м кроці xі(S) (причому у вже відому функцію Wі+1 (S) треба замість S підставити змінений стан).
– зробити умовну оптимізацію останнього (m-го) кроку, задаючись гамою станів S, з яких можна за один крок дійти до кінцевого стану, обчислюючи для кожного з них умовний оптимальний виграш по формулі.
– зробити умовну оптимізацію (m-1) – го, (m-2) – го й т.д. кроків по формулі, думаючи в ній й=(m-1), (m-2),…, і для кожного із кроків указати умовне оптимальне керування xі(S), при якому максимум досягається.
Помітимо, що якщо стан системи в початковий момент відомо (а це звичайно буває так), те на першому кроці варіювати стан системи не потрібно – прямо знаходимо оптимальний виграш для даного початкового стану S0. Це і є оптимальний виграш за всю операцію.
– зробити безумовну оптимізацію керування, «читаючи» відповідні рекомендації на кожному кроці. Взяти знайдене оптимальне керування на першому кроці; змінити стан системи по формулі; для знову знайденого стану знайти оптимальне керування на другому кроці х2* і т.д. до кінця.
У завданнях динамічного програмування економічний процес залежить від часу (від декількох періодів (етапів) часу), тому перебуває ряд оптимальних рішень (послідовно для кожного етапу), що забезпечують оптимальний розвиток усього процесу в цілому. Завдання динамічного програмування називаються багатоетапними або багатокроковими. Динамічне програмування являє собою математичний апарат, що дозволяє здійснювати оптимальне планування багатокрокових керованих процесів і процесів, що залежать від часу. Економічний процес називається керованим, якщо можна впливати на хід його розвитку. Керуванням називається сукупність рішень, прийнятих на кожному етапі для впливу на хід процесу. В економічних процесах керування полягає в розподілі й перерозподілі засобів на кожному етапі. Наприклад, випуск продукції будь-яким підприємством – керований процес, тому що він визначається зміною складу встаткування, обсягом поставок сировини, величиною фінансування й т.д. Сукупність рішень, прийнятих на початку кожного року планованого періоду по забезпеченню підприємства сировиною, заміні встаткування, розмірам фінансування й т.д., є керуванням. Здавалося б, для одержання максимального обсягу випускає продукції, що, найпростіше вкласти максимально можлива кількість засобів і використати на повну потужність устаткування. Але це привело б до швидкого зношування встаткування й, як наслідок, до зменшення випуску продукції. Отже, випуск продукції треба спланувати так, щоб уникнути небажаних ефектів. Необхідно передбачити заходи, що забезпечують поповнення встаткування в міру зношування, тобто по періодах часу. Останнє хоча й приводить до зменшення первісного обсягу випускає продукції, що, але забезпечує надалі можливість розширення виробництва. Таким чином, економічний процес випуску продукції можна вважати складається з декількох етапів (кроків), на кожному з яких здійснюється вплив на його розвиток.
Початком етапу (кроку) керованого процесу вважається момент ухвалення рішення (про величину капітальних вкладень, про заміну встаткування певного виду й т.д.). Під етапом звичайно розуміють господарський рік.
Динамічне програмування, використовуючи поетапне планування, дозволяє не тільки спростити рішення завдання, але й вирішити ті з них, до яких не можна застосувати методи математичного аналізу. Спрощення рішення досягається за рахунок значного зменшення кількості досліджуваних варіантів, тому що замість того, щоб один раз вирішувати складне різноманітне завдання, метод поетапного планування припускає багаторазове рішення щодо простих завдань.
Плануючи поетапний процес, виходять із інтересів усього процесу в цілому, тобто при ухваленні рішення на окремому етапі завжди необхідно мати у виді кінцеву мету.
Однак динамічне програмування має й свої недоліки. На відміну від лінійного програмування, у якому симплексний метод є універсальним, у динамічному програмуванні такого методу не існує. Кожне завдання має свої труднощі, і в кожному випадку необхідно знайти найбільш підходящу методику рішення. Недолік динамічного програмування полягає також у трудомісткості рішення багатомірних завдань. При дуже великому числі змінних рішення завдання навіть на сучасних ЕОМ обмежується пам'яттю й швидкодією машини. Наприклад, якщо для дослідження кожного змінного одномірного завдання потрібно 10 кроків, то у двовимірному завданні їхня кількість збільшується до 100, у тривимірної – до 1000 і т.д.
Припустимо, якась система S перебуває в деякому початковому стані S0 й є керованою. Таким чином, завдяки здійсненню деякого керування U зазначена система переходить із початкового стану S0 у кінцевий стан Sк. При цьому якість кожного з реалізованих керувань U характеризується відповідним значенням функції W(U). Завдання полягає в тім, щоб з безлічі можливих керувань U знайти таке U*, при якому функція W(U) приймає екстремальне (максимальне або мінімальне) значення W(U*).
Завдання динамічного програмування мають геометричну інтерпретацію. Стан фізичної системи S можна описати числовими параметрами, наприклад витратою пального й швидкістю, кількістю вкладених коштів і т.д. Назвемо ці параметри координатами системи; тоді стан системи можна зобразити крапкою S, а перехід з одного стану S1 в інше S2 – траєкторією крапки S. Керування U означає вибір певної траєкторії переміщення крапки S з S1 в S2, тобто встановлення певного закону руху крапки S.
Сукупність станів, у які може переходити система, називається областю можливих станів. Залежно від числа параметрів, що характеризують стан системи, область можливих станів системи може бути різної. Нехай, наприклад, стан системи S характеризується одним параметром, – координатою x. У цьому випадку зміна координати, якщо на неї накладені деякі обмеження, зобразиться переміщенням крапки S по осі Оx або по її ділянці. Отже, областю можливих станів системи є сукупність значень x, а керуванням – закон руху крапки S з початкового стану S0 у кінцеве Sk по осі Ox або її частини (рис. 1.1).
![]()
![]()
![]()
![]() S0 S Sk
S0 S Sk

![]()
![]() 0 x
0 x
Область можливих станів системи
Рисунок 1.1. Графічне зображення переходу системи S
Таким чином, завданню динамічного програмування можна дати наступну геометричну інтерпретацію. Із всіх траєкторій, що належать області можливих станів системи й з'єднуючих областей S0 й Sk, необхідно вибрати таку, на якій критерій W приймає оптимальне значення.
Щоб розглянути загальне рішення завдань динамічного програмування, уведемо позначення й зробимо для подальших викладів припущення.
Будемо вважати, що стан розглянутої системи S на K-м кроці (k=1, n) визначається сукупністю чисел X(k) =(x1(k), x2(k),…, xn(k)), які отримані в результаті реалізації керування uk, що забезпечило перехід системи S зі стану X(k-1) у стан X(k). При цьому будемо припускати, що стан X(k), у яке перейшла система S, залежить від даного стану X(k-1) і обраного керування uk і не залежить від того, яким образом система S прийшла в стан X(k-1).
Далі із уважати, що якщо в результаті реалізації k-го кроку забезпечені певний доход або виграш, що також залежить від вихідного стану системи X(k-1) і обраного керування uk і рівний Wk(X(k-1), uk), те загальний доход або виграш за n кроків становить
n
F=∑ Wk(X(k-1), uk) (1.1)
k=1
Таким чином, завдання динамічного програмування повинна задовольняти дві умови. Першу умову звичайно називають умовою відсутності післядії, а друге – умовою адитивності цільової функції завдання.
Виконання для завдання динамічного програмування першої умови дозволяє сформулювати для неї принцип оптимальності Беллмана. Перш ніж зробити це, треба дати визначення оптимальної стратегії керування. Під такою стратегією розуміється сукупність керувань U*=(u1*, u2*,…, un*), у результаті реалізації яких система S за n кроків переходить із початкового стану X(0) у кінцеве X(k) і при цьому функція (1.1) приймає найбільше значення.
Принцип оптимальності: яке б не був стан системи перед черговим кроком, треба вибрати керування на цьому кроці так, щоб виграш на даному кроці плюс оптимальний виграш на всіх наступних кроках був максимальним.
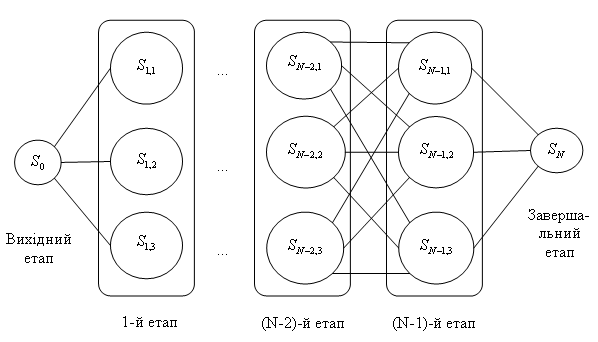
Звідси треба, що оптимальну стратегію керування можна одержати, якщо спочатку знайти оптимальну стратегію керування на n-м кроці, потім на двох останніх кроках, потім на трьох останніх кроках і т.д., аж до першого кроку. Таким чином, рішення розглянутого завдання динамічного програмування доцільно починати з визначення оптимального рішення на останньому, n-м кроці. Для того щоб знайти це рішення, мабуть, потрібно зробити різні припущення про те, як міг скінчитися передостанній крок, і з обліком цього вибрати керування un0, що забезпечує максимальне значення функції Wn(X(n-1), un). Таке керування un0 обране при певних припущеннях про те, як скінчиться попередній крок, називається умовно оптимальним керуванням. Отже, принцип оптимальності вимагає знаходити на кожному кроці умовно оптимальне керування для кожного з можливих варіантів попереднього кроку.
Щоб це можна було здійснити практично, необхідно дати математичне формулювання принципу оптимальності. Для цього введемо деякі додаткові позначення. Позначимо через Fn(X0) максимальний доход, одержуваний за n кроків при переході системи S з початкового стану X(0) у кінцевий стан X(k) при реалізації оптимальної стратегії керування U=(u1, u2,…, un), а через Fn-k(X(k)) – максимальний доход, одержуваний при переході з будь-якого стану X(k) у кінцевий стан X(n) при оптимальній стратегії керування на що залишилися n-k кроках. Тоді:
Fn(X0)=max[W1(X(0), u1)+ … + Wn(X(n-1), un)] (1.2)
Uk+j
Fn-k(X(k))=max[Wk+1(X(k), uk+1)+Fn-k-1(Xk+1))] (k=0, n-1) (1.3)
Uk+1
Останнє вираження являє собою математичний запис принципу оптимальності й зветься основного функціонального рівняння Беллмана або рекуррентного співвідношення. Використовуючи дане рівняння можна знайти рішення завдання динамічного програмування.
Думаючи k=n-1 у рекуррентном співвідношенні (1.3), одержимо наступне функціональне рівняння:
F1(X(n-1)=max[Wn(X(n-1), un)+F0(X(n))] (1.4)
un
У цьому рівнянні F0(X(n)) будемо вважати відомим. Використовуючи тепер рівняння (1.4) і розглядаючи всілякі припустимі із системи S на (n-1) – м кроці X1(n-1), X2(n-1),…, Xm(n-1),…, знаходимо умовні оптимальні рішення un0(x1(n-1)), un0(x2(n-1)),…, un0(xm(n-1)),…
і відповідні значення функції (1.4)
F10 (X1(n-1)), F10 (X2(n-1)), …, F10 (Xm(n-1)),…
Таким чином, на n-м кроці знаходимо умовно оптимальне керування при будь-якому припустимому стані системи S після (n-1) – го кроку. Тобто, у якому би стані система не виявилася після (n-1) – го кроку, буде відомо, яке варто прийняти рішення на n-м кроці. Відомо також і відповідне значення функції (2.4). Розглянемо функціональне рівняння при k=n-2:
F2(X(n-1))=max[Wn-1(X(n-2), un-1)+F1(X(n-1))] (1.5)
Un-1
Для того щоб знайти значення F2 для всіх припустимих значень X(n-2), необхідно знати Wn-1(X(n-2), un-1) і F1(X(n-1)). Що стосується значень F1(X(n-1)), те вони вже визначені. Тому потрібно зробити обчислення для Wn-1(X(n-2), un-1) при деякому відборі припустимих значень X(n-2) і відповідних керувань un-1. Ці обчислення дозволять визначити умовно оптимальне керування u0n-1 для кожного X(n-2). Кожне з таких керувань разом із уже обраним керуванням на останньому кроці забезпечує максимальне значення доходу на двох останніх кроках.
Послідовно здійснюючи описаний вище ітераційний процес, дійдемо до першого кроку. На цьому кроці відомо, у якому стані може перебувати система. Тому вже не потрібно робити припущень про припустимі стани системи, а залишається як тільки вибрати керування, що є найкращим з обліком умовно оптимальних керувань, уже прийнятих на всіх наступних кроках.
Таким чином, у результаті послідовного проходження всіх етапів від кінця до початку визначається максимальне значення виграшу за n кроків і для кожного з них знаходимо умовно оптимальне керування.
Щоб знайти оптимальну стратегію керування, тобто визначити шукане рішення завдання, потрібно тепер пройти всю послідовність кроків, тільки цього разу від початку до кінця. А саме: на першому кроці як оптимальне керування u1* візьмемо знайдене умовно оптимальне керування u10. На другому кроці знайдемо стан X1*, у яке переводить систему керування u1*. Цей стан визначає знайдене умовно оптимальне u20, що тепер уважається оптимальним. Знаючи u2*, знаходимо X2*, а виходить, визначаємо u3* і т.д. У результаті цього найдеться рішення завдання, тобто максимально можливий доход й оптимальну стратегію керування U*, що включає оптимальні керування на окремих кроках: U*= (u1*, u2*,…, un*).
Отже, зі знаходження рішення завдання динамічного програмування видно, що цей процес є досить громіздким. Тому більше складні завдання вирішують за допомогою ЕОМ.
Динамічне завдання по заміні встаткування можливо також вирішити й графічним методом. На осі Х відкладають номер кроку (к). на осі В – вік устаткування (t). Крапка (до-1; t) на площині відповідає початку К-ого кроку по експлуатації встаткування у віці t років.
![]() Будь-яка траєкторія переводящая крапку S (k-1; t) зі стану S0 S. Складається з відрізків, тобто із кроків відповідним рокам експлуатації. Потрібно вибрати таку траєкторію при якій витрати на експлуатацію будуть мінімальні. Якщо відомі залежність продуктивності встановленого на підприємстві встаткування від часу його використання R(t) і залежність витрат на ремонт устаткування при різному часі його використання S(t) і витрати пов'язані із придбанням нового обладнання, то показником ефективності в цьому випадку є прибуток яка максимізується.
Будь-яка траєкторія переводящая крапку S (k-1; t) зі стану S0 S. Складається з відрізків, тобто із кроків відповідним рокам експлуатації. Потрібно вибрати таку траєкторію при якій витрати на експлуатацію будуть мінімальні. Якщо відомі залежність продуктивності встановленого на підприємстві встаткування від часу його використання R(t) і залежність витрат на ремонт устаткування при різному часі його використання S(t) і витрати пов'язані із придбанням нового обладнання, то показником ефективності в цьому випадку є прибуток яка максимізується.
Похожие работы
... у формулу (2.11) і визначити наступний стан системи . Для зміненого стану знайти оптимальне управління , підставити у формулу (2.11) і так далі. Для і-гo стану , знайти і і т.д. [1]. 3. Оптимальний розподіл інвестицій, як задача динамічного програмування Інвестор виділяє кошти в розмірі умовних одиниць, котрі повинні бути розподілені між -підприємствами. Кожне і-те підприємство при і ...
... випадків, аварій, а з цим і простоїв на підприємстві, укріпити та створити культуру трудової діяльності. Виконання та розробка дипломного проекту “ Розробка дослідження системи керування електроприводом змінного струму дизель-потягу з використанням нейронних мереж ” відбувається за допомогою комп'ютера, тому питання охорони праці розглядаються щодо забезпечення здорових і безпечних умов роботи ...
... ї стійкості по покриттю запасів підприємства ВАТ «Дніпропетровськгаз» у 2005 –2007 роках РОЗДІЛ 3. ЕКОНОМІЧНІ МОДЕЛІ В ПРОГНОЗУВАННІ ПОКАЗНИКІВ ФІНАНСОВОЇ ЗВІТНОСТІ ПІДПРИЄМСТВА Прогнозування фінансово-економічних результатів операційної діяльності ВАТ «Дніпропетровськгаз» в курсовому дослідженні виконано з застосуванням кореляційно-регресійних економіко-математичних моделей, які спираються ...
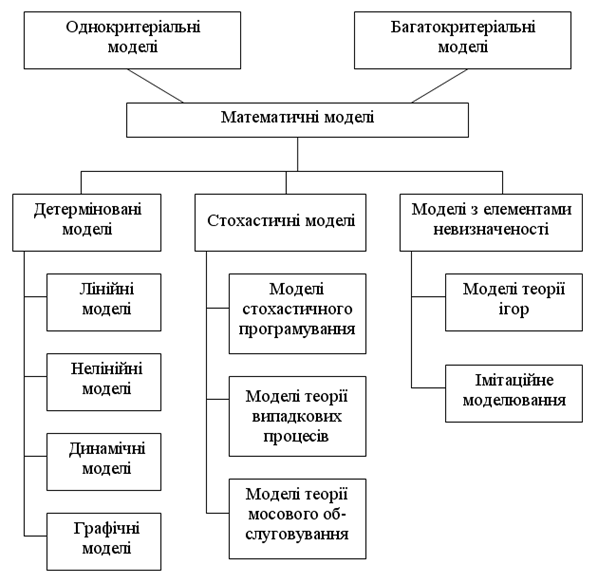
... ічно зростають показники ефективноств їх діяльності. Науково-дослідні інститути закордоном працюють над новими моделями, які раніше чи пізніше пристосуються до практики управління. Щоб якимось чином впорядкувати та зробити більш наочним питання про сфери застосування тих чи інших моделей і методів наведемо таблицю (див. табл.7).Таблиця 7: Сфери застосування моделей і методів обгруниування управлі ...



0 комментариев