Задача заміни обладнання

3. Задача заміни обладнання

3.1 Алгоритм рішення задачі заміни обладнання

У цьому завданні як система S виступає встаткування. Стан цієї системи визначаються фактичним часом використання встаткування (його віком) t, тобто описуються єдиним параметром t.

Як керування виступають рішення про заміну й збереження встаткування, прийняті на початку кожного року. Позначимо через Xc рішення про збереження встаткування, а через Xз – рішення про заміну встаткування. Тоді завдання полягає в знаходженні такої стратегії керування, обумовленої рішеннями, прийнятими на початок кожного року, при якій загальний прибуток підприємства за вісім років є максимальною.

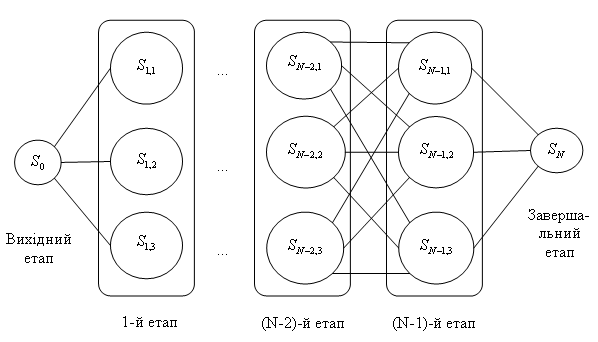
Процес рішення завдання здійснюється в такий спосіб. Береться період в N років. До цього часу встаткування відробило якусь кількість років і прийшло t0 віку.

Рішення завдання починається з останнього N-го року, складається пара функціональних рівнянь у припущенні, що прийшло старе встаткування без заміни:

1) розраховується доход від експлуатації встаткування при заміні;

2) розраховується доход від експлуатації встаткування протягом року за умови його старіння.

Друга гіпотеза: до N-ому року встаткування могло прийти заміненим у якомусь році, тоді складається пара рівнянь, у яких визначається доход за рік від експлуатації одиниці встаткування за умови заміни або збереження встаткування.

Крок другої: розглядаємо (N-1) рік.

Розглядаються дві гіпотези:

– прийшло старе встаткування без заміни;

– прийшло встаткування, що було замінено.

Крок третій: розглядається (N-2) рік при двох гіпотезах, складаються рівняння, розраховується доход.

Рішення триває по всіх кроках. На першому році буде одна гіпотеза, що прийшло старе встаткування, використовуване t0 років.

Під критерієм оптимальності може бути прийнятий будь-який економічний показник, якщо він добре підготовлений, тобто він повинен бути відчищений від факторів, що не залежать від роботи устаткування.

r(t) – вартість продукції, створеною одиницею устаткування віку t років за рік.

U(t) – витрати на протягом року одиниці встаткування віку t років.

С(t) – витрати на заміну одиниці устаткування віку t років (витрати на придбання, налагодження за винятком залишкової вартості старого встаткування).

і – рік установки нового обладнання.

Доход заміни встаткування розраховується:

f' = r(t) – U(t) – C(t) (3.1)

Доход від збереження встаткування:

f'' = r(t) – U(t) (3.2)

Якщо f' > f'', то встаткування необхідно замінити, якщо f' ≤ f'' – залишити.

Крок 1-й: N-й рік.

Гіпотеза 1: прийшло старе встаткування віку N+t0 років.

Тоді доход за N-й рік за умови заміни або збереження встаткування:

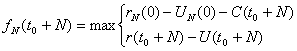 (3.3)

Гіпотеза 2: прийшло нове обладнання.

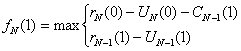 (3.4)

Візьмемо N-t-й рік:

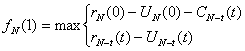 (3.5)

Крок 2-й: (N-1) – й рік.

Розраховується сумарний умовний доход, за умови заміни або збереження.

Гіпотеза 1: прийшло старе устаткування.

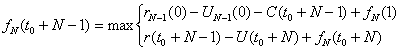 (3.6)

Гіпотеза 2: прийшло нове устаткування.

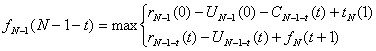 (3.7)

3.2 Контрольний приклад

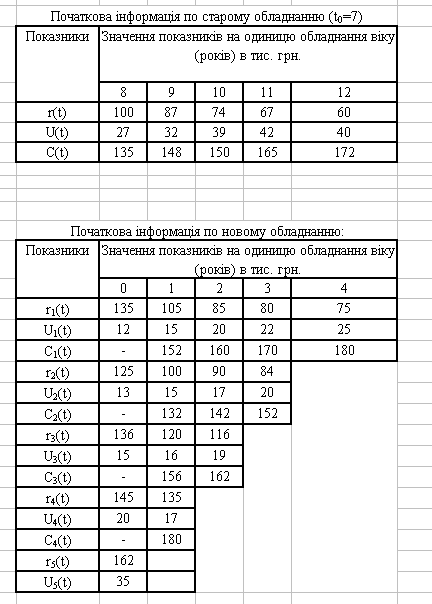
Для контрольного прикладу необхідно сформулювати дані про показники, які буде мати старе та нове обладнання на протязі певного періоду часу, в нашому випадку 5 років. Тобто, треба визначити, вартість продукції, виробленою одиницею обладнання за рік – r(t), витрати на експлуатацію обладнання протягом року – U(t), витрати на заміну одиниці устаткування – С(t) (див. Додаток А).

Задачу будемо розглядати в п’ять етапів. Тобто в кожному році ми будемо шукати найоптимальніші варіанти заміни обладнання.

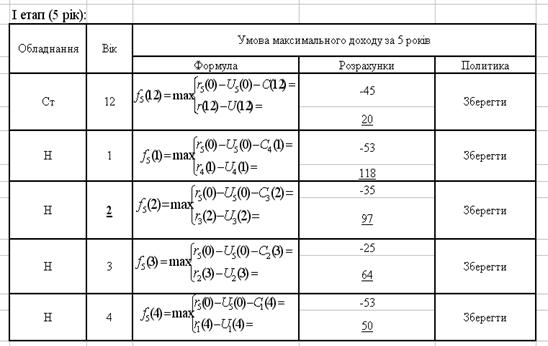
На першому етапі ми розраховуємо за п’ять років максимальний прибуток, тобто за t=12,1,2,3,4.

Розраховується за допомогою формул (3.3) та (3.4) відповідно до старого та нового обладнання. По розрахунках робимо висновок заміняти чи зберегти обладнання. На цьому етапі ми робимо висновок зберегти обладнання. (див. Додаток Б)

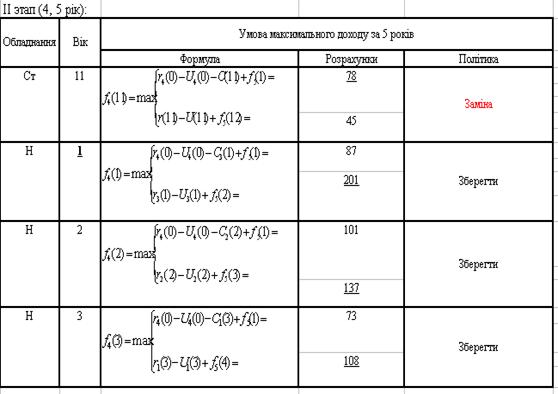
На другому етапі ми розраховуємо ефективність, коли t=11,1,2,3, для цього використовуємо формули (3.6) (3.7), також відповідно для нового та старого обладнання. Вирішуємо, що t=11 потрібно замінити, а інші залишити (див. Додаток В).

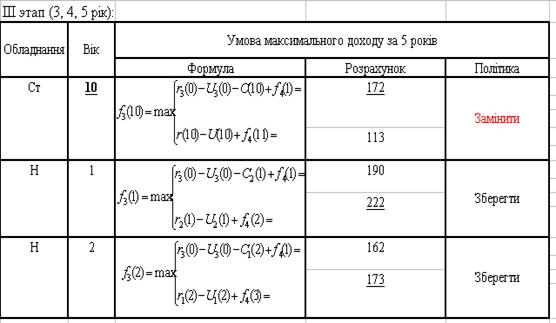
На третьому, четвертому та п’ятому етапі також використовуємо формули (3.6) та (3.7), відповідно до старого та нового обладнання, та робимо висновки, щодо заміни обладнання (див. Додаток Г, Д, Є).

Після розрахунку максимальних прибутків на кожному з етапів ми отримуємо:

– в 1 році зберегти обладнання, при цьому дохід складе (300–263)=37 тис. грн.;

– на 2 рік, зберегти при доході (263–172)=91 тис. грн.;

– на 3 році – змінити, при збитку (172–201)=55 тис. грн.;

– на 4 рік – зберегти, при доході (201–97)=104 тис. грн.,

– на 5 році – зберегти, при доході 97 тис. грн.

Така політика являється оптимальною. Вона забезпечує максимальний прибуток 300 тис. грн.

Висновки

Динамічне програмування – це область математичного програмування, що включає сукупність прийомів і засобів для знаходження оптимального рішення, а також оптимізації кожного кроку в системі й виробленні стратегії керування, тобто процес керування можна представити як багатокроковий процес. Динамічне програмування, використовуючи поетапне планування, дозволяє не тільки спростити рішення завдання, але й вирішити ті з них, до яких не можна застосувати методи математичного аналізу. Спрощення рішення досягається за рахунок значного зменшення кількості досліджуваних варіантів, тому що замість того, щоб один раз вирішувати складне різноманітне завдання, метод поетапного планування припускає багаторазове рішення щодо простих завдань. Плануючи поетапний процес, виходять із інтересів усього процесу в цілому, тобто при ухваленні рішення на окремому етапі завжди необхідно мати у виді кінцеву мету.

Однак динамічне програмування має й свої недоліки. На відміну від лінійного програмування, у якому симплексний метод є універсальним, у динамічному програмуванні такого методу не існує. Кожне завдання має свої труднощі, і в кожному випадку необхідно знайти найбільш підходящу методику рішення. Недолік динамічного програмування полягає також у трудомісткості рішення багатомірних завдань. Завдання динамічного програмування повинна задовольняти дві умови. Першу умову звичайно називають умовою відсутності післядії, а друге – умовою адитивності цільової функції завдання.

На практиці зустрічаються такі завдання планування, у яких помітну роль грають випадкових факторів, що впливають як на стан системи, так і на виграш. Існує різниця між детермінованою й стохастичним завданнями динамічного програмування. У детермінованому завданні оптимальне керування є єдиним і вказується заздалегідь як тверда програма дій. У стохастичним завданню оптимальне керування є випадковим і вибирається в ході самого процесу залежно від випадково сформованої ситуації. У детермінованій схемі, проходячи процес по етапах від кінця до початку, теж перебуває на кожному етапі цілий ряд умовних оптимальних керувань, але із всіх цих керувань, в остаточному підсумку здійснювалося тільки одне. У стохастичній схемі це не так. Кожне з умовних оптимальних керувань може виявитися фактично здійсненим, якщо попередній хід випадкового процесу приведе систему у відповідний стан.

Принцип оптимальності є основою поетапного рішення завдань динамічного програмування. Типовими представниками економічних завдань динамічного програмування є так називані завдання виробництва й зберігання, завдання розподілу капіталовкладень, завдання календарного виробничого планування й інших. Завдання динамічного програмування застосовуються в плануванні діяльності підприємства з урахуванням зміни потреби в продукції в часі. В оптимальному розподілі ресурсів між підприємствами в напрямку або в часі.

Опис характеристик динамічного програмування й типів завдань, які можуть бути сформульовані в його рамках, по необхідності повинне бути дуже загальним і трохи невизначеним, тому що існує неозора безліч різних завдань, що укладаються в схему динамічного програмування. Тільки вивчення великої кількості прикладів дає виразне розуміння структури динамічного програмування.

Перелік посилань

1. Акулич И.Л. Математичне програмування в прикладах і завданнях. – М.: Вища школа, 1993.

2. Дудорин В.И. Моделювання в завданнях керування виробництвом.-М.: Статистика, 1980.

3. Дослідження операцій в економіці: навчальний посібник для вузів / під ред. Кремера Н.Ш. – М.: Банки й Біржі, ЮНИТИ, 1997.

4. http://www.dis.ru/manag/arhiv/2002/

5. http://www.math.mrsu.ru/programs/ivt/e-learn/7.html#zachin

Додаток А

Додаток Б

Додаток В

Додаток Г

Додаток Д