Навигация
Огляд існуючих моделей оптимізації портфелю цінних паперів
1.2 Огляд існуючих моделей оптимізації портфелю цінних паперів
оптимізація цінний папір ризик
При спробі розв'язати пряму або обернену задачу виникає запитання: яким чином визначаються характеристики портфеля (доходність та ризик). На сьогоднішній день найбільш розповсюджені 2 моделі визначення характеристик портфеля: модель Марковіца та модель Шарпа. Обидві моделі створені і успішно працюють в умовах, що склалися у відносно стабільних західних фондових ринків. Нажаль, до їх числа український фондовий ринок поки що не входить. Через це була розпочата спроба створити модель, яка здатна успішно функціонувати в умовах фондового ринку, що формується, розвивається та реорганізується, яким є фондовий ринок України. Створена модель отримала назву Квазі-Шарп (була подобна до моделі Шарпа)[3]. Кожну модель буде розглянуто окремо.
1.2.1 Модель Марковіца
Модель Марковіца базується на тому, що показники прибутковості різних цінних паперів взаємопов'язані: із зростанням доходності одних паперів спостерігається одночасне зростання і по іншим паперам, треті залишаються без змін, а в четвертих, навпаки доходність знижується. Такий вид залежності не детермінований, тобто однозначно визначений, а є стохастичним, і називається кореляцією.
Модель Марковіца має наступні основні припущення:
за доходність цінних паперів приймається математичне очікування доходності;
за ризик цінних паперів приймається середнє квадратичне відхилення доходності;
вважається, що дані минулих періодів, які використані при розрахунках доходності і ризику, повністю відображають майбутні значення доходності;
ступінь і характер взаемозв'язку між цінними паперами виражається коефіцієнтом лінійної кореляції.
За моделлю Марковіца доходність портфеля цінних паперів — це середньозважена доходність паперів, його складових, яка визначається формулою:
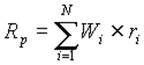 (1.1)
(1.1)
де N — кількість цінних паперів, які розглядаються;
Wi — процентна частка даного паперу в портфелі;
ri — доходність даного паперу.
Ризик портфеля цінних паперів визначається функцією:
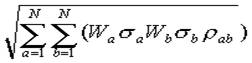 (1.2)
(1.2)
де Wi — процентна частка даних паперів у портфелі;
sa sb — ризик даних паперів (середньоквадратичне відхилення)
rab — коефіцієнт лінійної кореляції
З використанням моделі Марковіца для розрахунку характеристик портфеля пряма задача набуває вигляд:
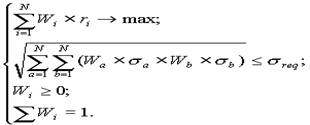 (1.3)
(1.3)
Обернена задача розраховується аналогічно:
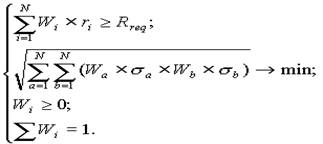 (1.4)
(1.4)
При застосуванні моделі Марковіца на практиці для оптимізації фондового портфеля використовуються наступні формули:
1) доходність цінних паперів:
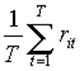 (1.5)
(1.5)
де T — кількість минулих спостережень доходності даних цінних паперів;
2) ризик цінного паперу:
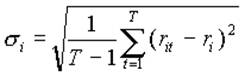 (1.6)
(1.6)
3) коефіцієнт кореляції між двома цінними паперами:
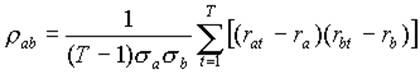 (1.7)
(1.7)
де rat, rbt — доходність цінних паперів а та b в період t
Зрозуміло, що для N цінних паперів необхідно розрахувати N(N-1)/2 коефіцієнтів кореляції.
Доходність цінних паперів складається з курсової різниці, дивідендних платежів, купонних платежів, дисконта тощо. В умовах сучасного фондового ринку України розраховувати на дивіденди поки що рано. Через це за доходність цінних паперів приймається відносна курсова різниця.
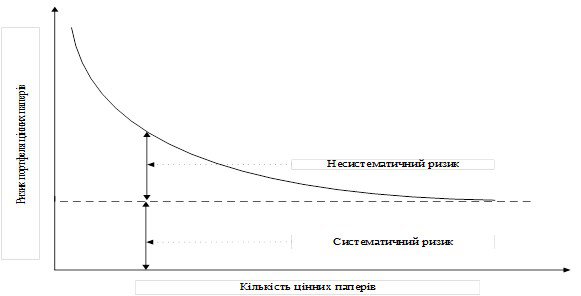
Модель Марковіца раціонально використовувати при стабільному стані фондового ринку, коли бажано сформувати портфель з цінних паперів різного характеру, що належать різним галузям. Основний недолік моделі – очікувана доходність цінних паперів приймається рівній середній доходності за даними минулих періодів.
1.2.2 Модель Шарпа
На відміну від моделі Марковіца, яка розглядає взаємозв'язок доходності цінних паперів, модель Шарпа розглядає взаємозв'язок доходності кожного цінного папера з доходністю ринку в цілому.
Основною перевагою моделі Шарпа є те, що математично обґрунтована взаємозалежність доходності та ризику: чим більший ризик, тим вища доходність цінного папера.
Модель Шарпа застосовується в основному при розгляді великої кількості цінних паперів, що описують велику частину фондового ринку. Основний недолік моделі – необхідність прогнозувати доходність фондового ринку та безризикову ставку доходності. Не враховується ризик коливань безризикової доходності. Крім того, при значній зміні співвідношення між безризиковою доходністю та доходністю фондового ринку модель дає похибки.
Основні припущення моделі Шарпа:
як доходність цінного папера береться математичне очікування доходності;
існує деяка безризикова ставка доходності Rf, тобто доходність якогось цінного папера, ризик якого завжди мінімальний у порівнянні з іншими цінними паперами;
взаємозв'язок відхилень доходності цінного папера від безризикової ставки доходності (далі відхилення доходності цінного папера) з відхиленням доходності ринку в цілому від безризиковоі ставки доходності (далі: відхилення доходності ринку) описується функцією лінійної регресії;
під ризиком цінного папера слід розуміти ступінь залежності змін доходності цінного папера від змін доходності ринку в цілому;
вважається, що дані минулих періодів, які використовуються при розрахунку доходності та ризику, відображають повною мірою майбутні значення доходності.
За моделлю Шарпа відхилення доходності цінного папера пов'язуються з відхиленнями доходності ринку функцією лінійної регресії виду:
(ri — Rf) = a + b(Rm — Rf) (1.8)
де (ri — Rf) — відхилення доходності цінного папера від безризикового;
(Rm — Rf) — відхилення доходності ринку від безризикового;
a, b — коефіцієнти регресії.
Виходячи з формули (1.8), можна по прогнозованій доходності ринку цінних паперів у цілому розрахувати доходність будь-якого цінного папера, що його складає:
Ri = Rf + ai + bi(Rm — Rf) (1.9)
Де ai, bi — коефіцієнти регресії, що характеризують даний цінний папір.
Коефіцієнт b називають b-ризиком, оскільки він характеризує ступінь залежності відхилень доходності цінного папера від відхилень доходності ринку в цілому. Основні переваги моделі Шарпа — математично обгрунтована взаємозалежність доходності та ризику: чим більший b-ризик, тим вища доходність цінного папера.
Крім того, модель Шарпа має особливість: існує небезпека, що оцінюване відхилення доходності цінного папера не належатиме побудованій лінії регресії. Цей ризик називають залишковим ризиком. Залишковий ризик характеризує ступінь розбросу значень відхилень доходності цінного папера навколо лінії регресії. Залишковий ризик визначають як середньоквадратичну відстань від точок доходності цінного папера до лінії регресії. Залишковий ризик і-го цінного папера позначають sei.
За моделлю Шарпа доходність портфеля цінних паперів — це середньозважена доходність цінних паперів, що його складають, з урахуванням b-ризику цінних паперів. Доходність портфеля визначається за формулою:
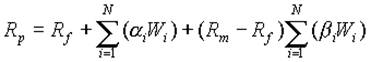 (1.10)
(1.10)
Де Rf — безризикова доходністъ;
Rm — очікувана доходність ринку в цілому.
Ризик портфеля цінних паперів може бути знайдений за допомогою оцінки середнього квадратичного відхиления функціі (1.10), і визначається за формулою:
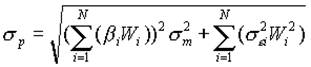 (1.11)
(1.11)
де sm — середньоквадратичне відхилення доходності ринку в цілому, тобто ризикованість ринку в цілому;
bi, sei — b-ризик і залишковий ризик і-го цінного папера.
При використанні моделі Шарпа для розрахунку характеристик портфеля пряма задача набуває вигляду:
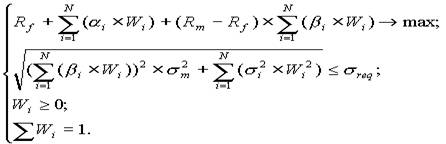 (1.12)
(1.12)
Зворотня задача виглядає аналогічним чином:
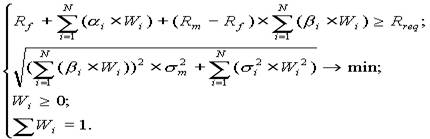 (1.13)
(1.13)
Основний недолік моделі — необхідність прогнозувати доходність фондового ринку та безризикову ставку доходності. Модель не враховуе ризик коливань безризикової доходності. Крім того, при значній зміні співвідношення між безризиковою доходністю та доходністю фондового ринку модель дає похибки.
Таким чином, модель Шарпа може застосовуватися при розгляді великої кількості цінних паперів, що описують велику частку відносно стабільного фондового ринку.
Похожие работы
... замінено на /2. Покладемо ,, k=k+1, j=1 та повернемося до першого кроку. Блок-схема алгоритму приведена нижче. Рисунок 2.4–Алгоритм Хука-Дживса 3. Розробка програмного забезпечення вирішення задачі формування портфеля цінних паперів 3.1 Загальні відомості про програмне забезпечення Розроблене програмне забезпечення призначене для автоматизації процесу формування портфелем цінних ...
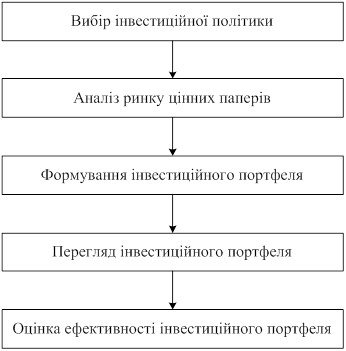
... захисту комерційного банку від можливого ризику зниження балансової вартості цінних паперів. Тобто необхідно проаналізувати сформовані резерви по операціях із цінними паперами. 2. Управління процесом формування портфеля цінних паперів банку Визначення цілей фінансового інвестування і типу портфеля, що реалізує обрану політику, дає змогу перейти безпосереднього до формування портфеля цінних ...
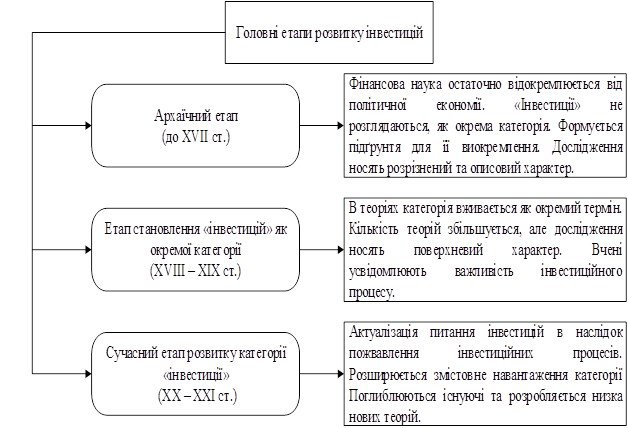
... паперів у певний час неефективний, застосування такого методу замість бажаного позитивного результату може завдати суттєвих збитків. 1.3. Портфельна теорія в якості основи для формування портфеля цінних паперів інвестиційної компанії У другій половині XX ст. в економіці розвинутих країн відбулися значні зміни, що було зумовлено пожвавленням інвестиційних процесів. Під впливом глобалізації сукупні ...
... аналізу прибутку в банку Рисунок 2.9 – Основні системи аналізу прибутку, що використовуються в банку Таблиця 2.9 – Основні показники коефіцієнтного аналізу прибутку 3 ФІНАНСОВИЙ МЕНЕДЖМЕНТ (НА ПРИКЛАДІ АКБ "ПРАВЕКС-БАНКУ") 3.1 АКБ "ПРАВЕКС-БАНК" – БАНК НАЦІОНАЛЬНОГО МАСШТАБУ Правекс-Банк є багатофункціональним фінансовим інститутом, який надає повний спектр банківських послуг як ...


0 комментариев