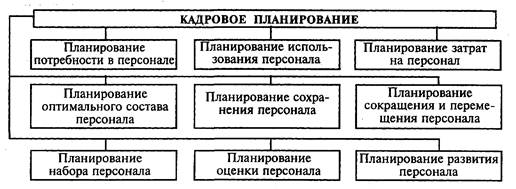
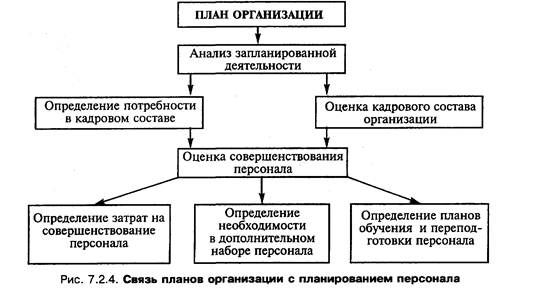
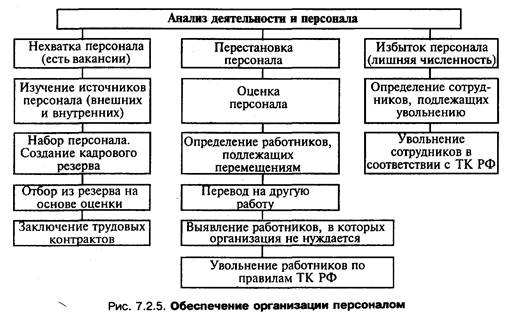
Навигация
Основной капитал как процент продажи свидетельствует о том, сколь успешно используются основные фонды предприятия (рентабельность)
4. Основной капитал как процент продажи свидетельствует о том, сколь успешно используются основные фонды предприятия (рентабельность).
Расчеты оптимального использования ресурсов. Успешность решения подавляющего большинства экономических задач зависит от наилучшего, наивыгоднейшего способа использования ресурсов. В процессе экономической деятельности приходится распределять такие важные ресурсы, как деньги, товары, сырье, оборудование, рабочую силу и др. И от того, как будут распределяться эти, как правило ограниченные, ресурсы, зависит конечный результат деятельности, бизнеса.
Суть методов оптимизации заключается в том, что исходя из наличия определенных ресурсов выбирается такой способ их использования (распределения), при котором обеспечивается максимум (или минимум) интересующего нас показателя. При этом учитываются определенные ограничения, налагаемые на использование ресурсов условиями экономической ситуации.
В качестве методов оптимизации в экономике находят применение все основные разделы математического программирования (планирования): линейное, нелинейное и динамическое.
Линейное программирование (планирование) – математический метод отыскивания максимума или минимума линейной функции при наличии ограничений в виде линейных неравенств или уравнений. (Линейное здесь означает, что на графике функции изображаются в виде прямых линий, обозначающих 1-е степени соответствующих величин.)
Максимизируемая (минимизируемая) функция представляет собой принятый критерий эффективности решения задачи, соответствующий поставленной цели. Она носит название целевой функции.
Ограничения характеризуют имеющиеся возможности решения задачи.
Существо решения задач линейного программирования заключается в нахождении условий, обращающих целевую функцию в минимум или максимум.
Решение, удовлетворяющее условиям задачи и соответствующее намеченной цели, называется оптимальным планом.
Линейное программирование (планирование) служит для выбора наилучшего плана распределения ограниченных однородных ресурсов в целях решения поставленной задачи.
В общем виде постановка задачи линейного программирования заключается в следующем.
Условия задачи представляются с помощью системы линейных уравнений или неравенств, выражающих ограничения, налагаемые на использование имеющихся ресурсов.
где Xj – искомые величины, содержащие решение поставленной задачи;
aij и bi – известные постоянные величины, характеризующие условия задачи.
Условия задачи (ограничения) могут быть заданы также в виде неравенств. В этих случаях можно привести систему линейных ограничений к виду (16.10), вводя в каждое линейное ограничение дополнительные неотрицательные неизвестные:
![]()
Целевая установка оптимизации заключается в том, чтобы свести ожидаемые при решении данной задачи издержки предприятий к минимуму.
Требуется обратить в минимум величину
![]()
где сj – показатель, характеризующий издержки предприятий.
Пусть т – общее число различных видов ресурсов, которыми располагает собственник, а п – число типов предприятий, между которыми эти ресурсы должны быть распределены. При этом известно, какое количество однородных ресурсов различного вида (i = 1, 2,... т) может быть реализовано на каждом из предприятий данного типа (j = 1, 2,... п), а также общее количество ресурсов данного вида (bi). Известно также относительное значение издержек на каждом из предприятий (cj).
Задача заключается в том, чтобы наилучшим (оптимальным) образом распределить имеющиеся ресурсы по предприятиям, т. е. найти неизвестные величины xj, требуемые для этого количества предприятий данного типа.
ПРИМЕР. Собственник располагает четырьмя видами ресурсов (m = 4). Это, например, денежные средства, производственные помещения, оборудование, сырье. Ресурсы необходимо распределить между шестью предприятиями (п = 6). Предприятия различаются по экономическим условиям деятельности: месту расположения, системе налогообложения, стоимости энергии, оплате труда и т. д., в связи с чем имеют разные издержки производства. Относительные уровни издержек заданы табл. 2.Таблица 2
Относительные уровни издержек на предприятиях
| Предприятия | 1 | 2 | 3 | 4 | 5 | 6 |
| Издержки | 0,4 | 0,5 | 0,2 | 0,8 | 0,6 | 0,3 |
Распределение ресурсов по предприятиям сопряжено с необходимостью учета ряда ограничений, которые могут быть описаны системой четырех уравнений с шестью неизвестными, аналогичной системе:
Смысл первого уравнения в нашем примере в том, что ресурс вида 1, общий ресурс которого составляет 16 единиц, может размещаться в количестве четырех единиц на предприятии первого типа и одной единицы – на предприятии четвертого типа. Аналогично раскрывается смысл второго и последующих уравнений. Последнее условие говорит о том, что число предприятий не может быть отрицательным.
Необходимо определить, какое количество предприятий каждого типа следует иметь, чтобы общие издержки были минимальными.
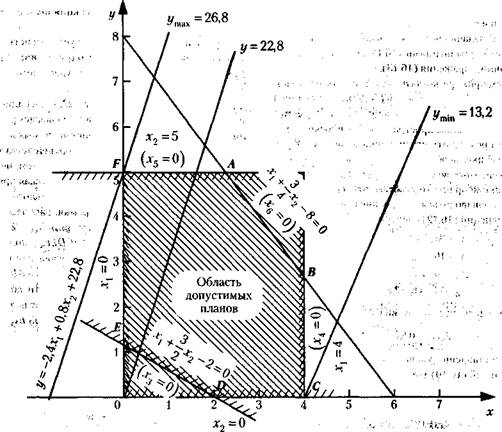
Рис. 1. График оптимального распределения ресурсов
В нашем примере, когда п - т = 2, каждое из ограничительных линейных уравнений, а также линейная функция могут быть представлены геометрически в двухмерном пространстве (на плоскости).
Чтобы представить ограничения и целевую функцию на графике, необходимо выразить все известные через независимые величины. Например, x1 и х2, соответствующие координатным осям, относительно которых будет производиться построение (рис. 1).
Каждому из неравенств на графике рис. 1 соответствует полуплоскость, в пределах которой находятся все допускаемые данным неравенством значения переменной величины xj (j = 1, 2,..., 6). Так, неравенству x1³ 0 соответствует полуплоскость вправо от оси х2 (граница ее заштрихована). Неравенству x3= 8x1 + 12х2 - 16 ³ 0 соответствует полуплоскость вправо и вверх от линии граничного значения данного неравенства (при х3 = 0). Уравнение этой линии:
![]()
Таким же образом можно построить границы, определяемые другими уравнениями.
Неравенствам соответствует некоторая область – шестиугольник ABCDEF, образованный границами упомянутых выше полуплоскостей. Эта область может быть названа областью допустимых планов, поскольку любая точка в ее пределах отвечает требованиям наложенных ограничений.
Из всех допустимых планов нас интересует оптимальный план, при котором функция цели у достигает минимума.
Целевой функции соответствует семейство параллельных прямых. Рассмотрим одну из них, проходящую через начало координат, что будет иметь место при у = 22,8. При этом x2 = 3x1.
Интересующая нас прямая у = 22,8, как видно на рис. 16.1, имеет наклон вправо от оси х2. Задаваясь различными значениями у, получим семейство прямых линий, параллельных прямой у = 22,8, проходящей через точку 0. При этом чем меньше будет значение у, тем, очевидно, правее будет располагаться соответствующая прямая.
Поскольку мы добиваемся минимального значения у, то нас будет интересовать прямая, расположенная в наибольшем удалении вправо от прямой у = 22,8 и проходящая через многоугольник ABCDEF, – прямая ymin.
Единственной точкой, соответствующей оптимальному плану, будет та вершина многоугольника ABCDEF, которая одновременно принадлежит области допустимых планов и отвечает требованию минимизации целевой функции у, - вершина С. Из уравнения прямой ЕС, проходящей через точку С, следует, что х1 = 4. Из уравнения прямой DC, проходящей через ту же точку, следует, что x2 = 0.
Подставляя полученные значения x1 = 4 и x2 = 0 в уравнения, определим величины остальных переменных, составляющих оптимальный план:
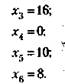
Таким образом, оптимальный план будет следующим:
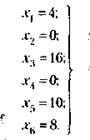
Линейная форма (величина издержек) при этом будет минимальной:
![]()
На практике встречается ряд задач, аналогичных рассмотренному примеру, но требующих максимизации целевой функции (например, величины дохода или прибыли).
При решении этих задач целевая функция рассчитывается по формуле:
![]()
где у* – целевая функция, подлежащая максимизации. Отличие заключается в том, что знаки перед всеми постоянными коэффициентами меняются на обратные
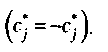
Библиографический список
1. Управление в гибком производстве (в соавт.).– М.: Радио и связь, 2010.-126 с.
2. Основы математического программирования. – М.: ВОК, 2006.-89 с.
3. Автоматизация управления (в соавт.). – М.: Радио и связь, 2009. – 262 с.
4. Основы исследования операций. – М.: ВОК, 2007.-316 с.
5. Разработка систем управления (в соавт.). – М.: ЛИМТУ, 2009.-83 с.
6. Введение в теорию выработки решений (в соавт.). - М: В-дат, 2008.- 39 с.
7. Основы теории игр и статистических решений (в сб.). - М.: ВОК, 2006. - 91 с.
8. Справочник по исследованию операций (в соавт.). - М.: В-дат, 2008. - 361 с.
9. Уроки бизнеса. – СПб.: Образование, 2008. – 190 с.
10. Принятие решений в услових неполной информации. - М.: ЛИМТУ 2007.
Похожие работы
... мышление, способность принимать самостоятельные решения, высокую степень независимости, активность, стремление к саморазвитию. Заключение В результате проведённого исследования по теме: „Анализ качества и эффективности менеджмента на предприятии (организации, фирме)“ можно сделать следующие выводы: 1. В современных условиях залогом преуспевания предприятий и фирм становятся гибкость, ...
... собой оценочную систему показателей эффективности функционирования системы менеджмента организации. 2. Реинжиниринг (БПР – Business process reengineering) Повышение эффективности менеджмента организации, прежде всего, связано с кардинальным усовершенствованием бизнес-процессов компании, или ее реинжинирингом (БПР – Business process reengineering) . Понятие реинжиниринга возникло в 1990 г. ...
... Результат — рост социальной напряженности, снижение инициативы и мотивации к высокопроизводительному труду, кризис доверия. Все это может стать серьезным тормозом столь необходимых преобразований. 3.Эффективный менеджмент в условиях российской действительности Рассмотрим, как на практике современные российские предприятия сумели организовать эффективное управление, базирующееся на опыте Востока ...
... , персонала и клиентов. Поэтому организационное совершенствование и управление персоналом становится одной из главнейших функций менеджмента организации, обеспечивающих его эффективность. Естественно, система управления персоналом зависит от структуры управления предприятием — является ли предприятие самостоятельным или это холдинговая структура, состоящая из материнской компании и многих ...


0 комментариев