Навигация
2. Модуль Graph
Турбо Паскаля містить близько п'ятдесяти різних процедур та функції, призначених для роботи з графічним екраном. У цьому ж модулі деякі вбудовані константи, які можуть бути використані в графічних програмах. Для того щоб скористатися всіма можливостями модуля Graph, на початку програми (після заголовка) необхідно помістити оператор використання Uses Graph; Основну частину модуля складають процедури введення базових графічних елементів, таких як точки, відрізки прямих ліній, Дуги і цілі кола та ін. Функція GraphErrorMsg. Повертає значення типу String, в якому за вказаним кодом помилки дається відповідне текстове повідомлення. Заголовок:Functional GraphErrorMsg (Code: Integer): String; Тут Code - код помилки, що повертається функцією GraphResult. Функція CloseGraph. Завершує роботу адаптера в графічному режимі і відновлює текстовий режим роботи екрану.
2.1 Опис деяких графічних процедур і функцій
1)Ellipse (X, Y: Integer; U1, U2, XR, YR: Word) Малює дугу еліпса поточним кольором; X, Y - координати центру еліпса; U1, U2 - кути до початкової і кінцевої точок дуги еліпса (див. процедуру Arc) ; XR, YR - горизонтальна і вертикальна півосі еліпса. 2)FillEllipse (X, Y: Integer; XR, YR: Word) Малює заштрихований еліпс, використовуючи X, Y як центр і XR, YR як горизонтальну і вертикальну півосі еліпса. 3)Line(X1,Y1, X2,Y2:Integer)Малює лінію від точки X1,Y1 до точки X2, Y2. 4)LineTo(X,Y:Integer)Малює лінію від поточного покажчика до точки X,Y. 5)SetBkColor (Соlor: Word) Встановлює колір фону.
2.2 Робота в графічному режимі
Перш, ніж приступити до створення графічних програм на Turbo Pascal, необхідно ознайомитися з найбагатшими графічними можливостями цієї мови, зосередженими в стандартних модулях (бібліотеках) GRAPH і CRT (CRT назва походить від Cathode-Ray Tube - електронно-променева трубка). Ці модулі містять опису стандартних констант, процедур і функцій, графічному режимі. При роботі в графічному режимі весь екран розбивається на окремі точки - "пікселі". Положення піксела також задається двома координатами - X і Y. Координата X збільшується зліва направо, а координата Y - зверху вниз. Підключення модулів CRT і GRAPH до програми здійснюється за допомогою ключового слова Uses (англ.uses - використовує) Uses Crt, Graph.
3. Модуль CRT
Модуль CRT містить опису констант,процедур і функцій, що забезпечують керування текстовим режимом роботи монітора і звуковим генератором.
3.1 Процедури
1)ClrScr- Очищає екран або вікно і поміщає курсор у верхній лівий кут. 2)Delay(D: Word)- припиняє роботу програми на вказане число D мілісекунд. Практично час затримки залежить від тактової частоти процесора. 3)GotoXY (X, Y: Byte)- переміщає курсор в позицію X рядка Y екрану. 4)NoSound-Вимикає джерело звуку. 5)Sound (F: Word)- запускає джерело звуку з частотою F (Гц). 6)TextBackGround (Color: Byte)- встановлює колір фону. 7)TextColor (Color: Byte)- встановлює колір символів. 8)Window(X1, Y1, X2, Y2: Byte)- визначає текстове вікно на екрані. X1, Y1 - координати лівого верхнього кута вікна, X2, Y2 - правого нижнього кута вікна.
3.2 Опції
1)KeyPressed: Boolean Аналізує натискання клавіші. Результат TRUE, якщо на клавіатурі натиснута клавіша (крім Alt, Ctrl і т.п.), і FALSE в іншому випадку. Чи не затримує виконання програми. 2)ReadKey: Char Читає символ з клавіатури без ехоповтора на екрані. Припиняє виконання програми, перш ніж натиснути на будь-яку клавішу, крім Alt, Ctrl і т.п.
4.Лістинг Програми
Program grapik;
Uses Crt, Graph;
const A=-100;B=100;XO=0;YO=0;
N=100;
var gd,gm,sgr,left,up,down,right,xgo,ygo,i:integer;
x, y :array [1..300] of real;
xg, yg: array [1..300] of integer;
Kx, Ky, Y_min, Y_max, X_min, X_max, Dx:real;
begin
gd:=0;gm:=0;
initgraph (gd,gm,'C:\tp70\bgi');
SetBkColor (3);
left:=40; up:=40; down:=440;
X_min:=A; X_max:=B;
Dx:=(B-A)/(N-1);
for i:=1 to N do begin
X[i]:=A+round(Dx*(i-1));
Y[i]:=1+X[i];
end;
Y_max:=Y[1];
Y_min:=Y[1];
for i:=1 to N do begin
if Y_max<Y[i] then Y_max:=Y[i];
if Y_min>Y[i] then Y_min:=Y[i];
end;
begin
Ky:=(down-up)/(Y_max-Y_min);
Kx:=Ky;
right:=left+round(Kx*(X_max-X_min));
if right>GetMaxX then
begin
right:=GetMaxX;
Kx:=(right-left)/(X_max-X_min);
Ky:=Kx;
up:=(down-round(Ky*(Y_max-Y_min)));
end;
for i:=1 to N do begin
Xg[i]:= left+round(Kx*(X[i]-X_min));
Yg[i]:= down-round(Ky*(Y[i]-Y_min));
end;
MoveTo (Xg[i], Yg[i]);
for i:=2 to N do
LineTo (Xg[i], Yg[i]);
XGO:=left+round(Kx*(XO-Y_min));
YGO:=down-round(Ky*(YO-Y_min));
Line(XGO,up,XGO,down);
Line(left,YGO,right,YGO);
for i:= 1 to N do
y[i]:=x[i]*x[i];
X_max:=y[1];
Y_min:=y[1];
for i:= 1 to N do
begin
if Y_max<y[1] then y_max:=y[1];
if Y_min>y[i] then y_min:=y[i];
end;
for i:=1 to N do
begin
xg[i]:=(left+round(Kx*(x[i]-x_min)));
yg[i]:=(down-round(Ky*(y[i]-x_min)));
end;
MoveTo (xg[i], yg[i]);
for i:=2 to N do
LineTo (xg[i], yg[i]);
End;
xg[i]:=yg[i];
for i:=1 to N do
MoveTo (xg[i],yg[i]);
LineTo (left, yg[i]);
readln;
closegraph;
end.
Висновок
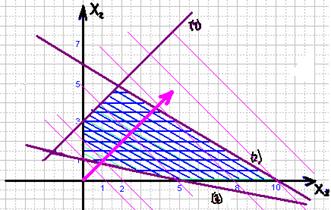
У цій роботі описуються розв’язок систем нерівностей призначених для створення графіків в графічному середовищі Турбо Паскаля. Використовуючи вище перераховані процедури та функції, я навчився зображати графіки систем нерівностей, так само зміг показати переріз цих графіків. Написавши дану програму, я отримав навички роботи в графічному середовищі Турбо Паскаль, навчився правильно застосовувати різні процедури та функції, точно визначати і задавати координати графіків.
Блок–схема

Математична модель

![]()
![]()




![]()

![]()
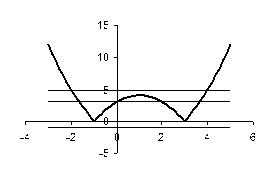
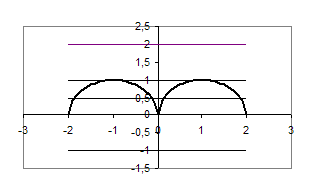
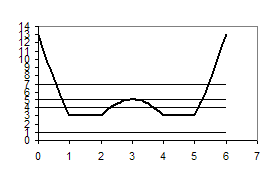
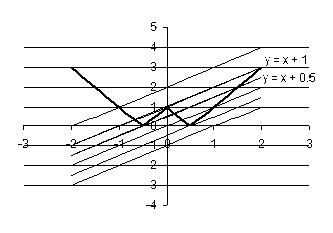
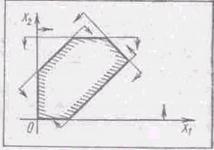
![]() y – x2 ≥ 0,
y – x2 ≥ 0,

![]()

 y – x ≥ 1;
y – x ≥ 1;
![]()
![]() y=x2,
y=x2,
y= 1+x;
y=x2:
(0; 0), (2; 4);
y=1+x:
(2; 3), (1; 2).
Список використаних джерел
1)Е. А. Зуєв. Програмування на мові Turbo Pascal 6.0, 7.0, М.: Веста, Радіо і зв'язок, 1993, - С.376
2)Turbo Pascal: вчиться програмувати, О. А. Меженний, Москва:
Изд.дом «Вільямс», 2001
3)Основи мови Turbo Pascal (навчальний курс), П. И. Рудаков, М. А.Федотов, Москва: Радіо та зв'язок, 2000р.
4)Моргун Олександр Миколайович. Довідник по Turbo Pascal для студентів. - М.: Діалектика, 2006. - С. 608.
Похожие работы
... х та у для позначення осей, визначає один з ефективніших методів розв’язку задач з параметрами. Для того, щоб найбільш повно розкрити можливості цього метода, покажемо його застосування для розв’язування основних типів задач з параметрами. Дамо самі загальні признаки, які, можливо, допоможуть впізнавати задачі, які підходять під цей метод: в задачі фігурують лише один параметр а та одна змінна ...
... зумовлюється метою, якої хочуть досягти даною геометричною інтерпретацією та особливостями структури самої задачі, в тому числі й формою її представлення. Для геометричної інтерпретації візьмемо основну задачу лінійного програмування у другій стандартній формі. Для наочності розглянемо найпростіший випадок, коли в системі обмежень (26) і цільовій функції (25) є лише дві змінних, Розглянемо розв' ...
... «Поганий учитель підносить істину, хороший вчить її знаходити» (А. Дістервега), завдання вчителя - «навчити вчитися», «не наповнити посудину», а «запалити факел» (Сократ). 3. Методика навчання розв’язання логарифмічних рівнянь та нерівностей 3.1 Логарифмічні рівняння При введенні поняття логарифму і властивостей логарифмічної функції необхідно значну увагу приділити вмінню застосовувати ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...





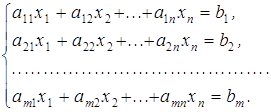
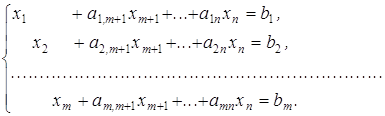
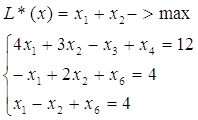
0 комментариев