Навигация
Procedure WritePoints(var P:P_Descriptor);
1 Procedure WritePoints(var P:P_Descriptor);
2) Назначение: выводит весь список точек P на дисплей;
3) Входные параметры: P;
4) Выходные параметры: P.
4.Спецификация процедуры ReadPoint;
1) Procedure ReadPoint(var P:P_Descriptor;var a:Coordinates);
2) Назначение: cчитывает из списка P координаты точки в переменную а;
3) Входные параметры: P;
4) Выходные параметры: P,a.
5.Спецификация процедуры ClearMem;
1) Procedure ClearMem(var P:P_Descriptor;var V:V_Descriptor);
2) Назначение: освобождает выделенную память под списки P u V;
3) Входные параметры: P,V;
4) Выходные параметры: P,V.
Спецификация подпрограмм для работы с векторами
1.Спецификация процедуры CreateVector;
1) procedure CreateVector (a,b:Coordinates;var c:Coordinates);;
2) Назначение: создает вектор с вычитая соответствующие координаты точки b из точки a;
3)Входные параметры: a,b,c
4)Выходные параметры: c.
2.Спецификация процедуры MultOnNumber;
1) Procedure MultOnNumber (Number:real; a:Coordinates;var c:Coordinates)
2)Назначение: умножает вектор a на число real и полученное значение заносится в c вектор ;
3)Входные параметры: Number,a,c;
4)Выходные параметры: ,c;
3.Спецификация процедуры lengthOfVector;
1 Function lengthOfVector(a:Coordinates):real;
2Назначение: возвращает длину вектора а ;
3Входные параметры: а;
4Выходные параметры: -.
4.Спецификация процедуры Scalar;
1) Function Scalar(a,b:Coordinates):real;
2Назначение: возвращает результат скалярного перемножение векторов а и b ;
3Входные параметры: a,b;
4Выходные параметры: -.
5.Спецификация процедуры angle;
1) Function angle(a,b:coordinates):real
2Назначение: возвращает значение косинуса угла(в радианах)
между векторами а и b
3Входные параметры: a,b;
4Выходные параметры: -.
6.Спецификация процедуры VECTMult;
1 Procedure VECTMult(a,b:Coordinates;var c:Coordinates);
2Назначение: производит векторное перемножение вектора а и b и заносит результат в вектор с ;
3Входные параметры: а,b,c ;
4Выходные параметры: c.
7.Спецификация процедуры collinearity;
1) Function collinearity(a,b:Coordinates):boolean;
2Назначение: возвращает collinearity:=истина , если векторы а и b коллинеарные, иначе- collinearity:=ложь ;
3Входные параметры: a,b;
4Выходные параметры: -.
5 возврат : collinearity
9.Спецификация процедуры MixeMult;
1) Function MixeMult(a,b,c:Coordinates):real
2Назначение: возвращает MixeMult:= значение смешанного произведения векторов а и b
3Входные параметры: a,b;
4Выходные параметры: -.
5Возврат : MixeMult
10.Спецификация процедуры coplanarity;
1) Function coplanarity(a,b,c:Coordinates):boolean
2Назначение: возвращает coplanarity :=истина ,если векторы а,b и c компланарны,иначе- coplanarity :=ложь .
3Входные параметры: a,b,c;
4Выходные параметры: -.
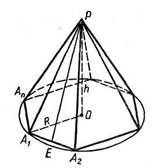
Спецификация подпрограмм для определения вершин пирамиды
1.Спецификация процедуры ploskost
1) Procedure ploskost(a,b,c:coordinates;var ax,bx,cx,dx:real);;
2) Назначение: Строит по 3-м точкам уравнение плоскости вида Ax+By+Cz+D=0 и заносит в ax,bx,cx,dx соответствующие коэффициенты
3) Входные параметры:a,b,c,ax,bx,cx,dx;
4) Выходные параметры: ax,bx,cx,dx.
2.Спецификация функции proverka_na_ploskost;
1) function proverka_na_ploskost(var P:P_descriptor;var mno:mnoj; n:byte):boolean;;
2) Назначение: проверяет условие принадлежности n точек(указатели которых хранятся в множестве mno) к плоскости ,построенной с помощью процедуры ploskost,возращает значение истины в случае удачной проверки, иначе-ложь;
3) Входные параметры: P,mno,n;
4) Выходные параметры: P,mno.
5) Возврат : f
3.Спецификация функции Vypuklost;
1) Function Vypuklost(var P:P_descriptor;mno:mnoj;n:byte):boolean;;
2) Назначение: Проверяет многоугольник на выпуклость, путем перебора n точек из множества mno ,формированием их в векторы и последующим векторным перемножением . Возвращает значение истины, если при все N точках знак векторного умножения сохраняется, иначе -ложь;
3) Входные параметры: P,mno,n;
4) Выходные параметры: P.
5) Возврат : Q
4.Спецификация функции FinDaPyramid;
1) Procedure FinDaPyramid(var P:P_descriptor;mno:mnoj);
2) Назначение: определяет вершины пирамиды с выпуклым основанием и выводит на дисплей, если же нет решений -выводит соотсветсвующее сообщение ;
3) Входные параметры: P,mno,n;
4) Выходные параметры: P,mno.
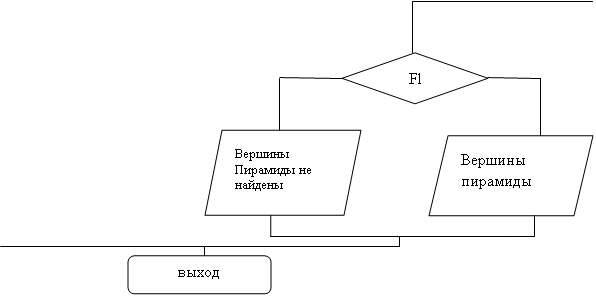
Блок-схема
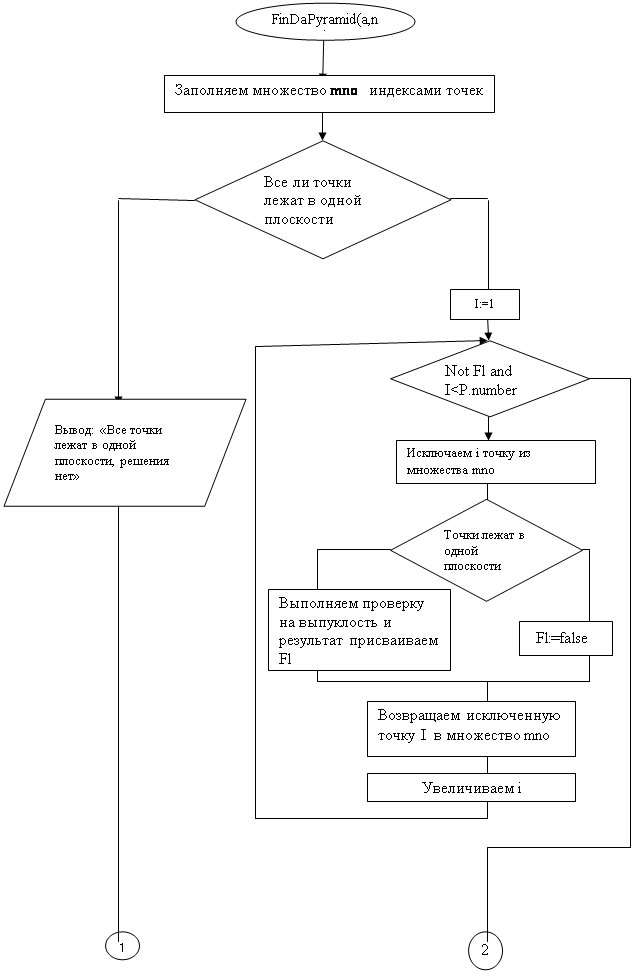
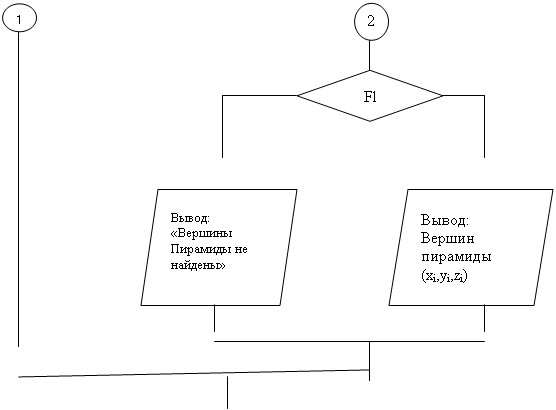 | |||
Тестовые Данные
-Введем 5 точек
Точка 1(2,-1,-1)
Точка 2(1, 2, 3)
Точка 3(4, 1 1)
Точка 4(0, 1, 2)
Точка 5(7, 1, 1)
-Построим по 3-м точкам уравнение плоскости
Уравнение каждой плоскости имеет вид: Ax + By + Cz + D = 0. Так что наша задача по заданным координатам 3-ех точек плоскости найти коэффициенты A, B, C и D. Эти коэффициенты находятся по формулам:
![]()
где x, y, z - координаты наших точек, а 1-2-3 это номера точек A-B-C.
Соответственно находим эти коэффициенты и подставляем их в формулу
--В итоге, получаем уравнение вида Ax + By + Cz + D = 0.
A = -2
B = 10
C = -8
- D = -6
Подставим коэффициенты. Уравнение плоскости:
-2 x + 10 y - 8 z + 6 = 0
Далее, проверим 4 и 5 точку на принадлежность к этой плоскости:
Берем точку 4(0, 1, 2) и подставляем в уравнение -2 x + 10 y - 8 z + 6 = 0
-2(0)+10(1)-8(2)+6=0
0=0
Точка 4 принадлежит плоскости.
Берем точку 5(7, 1, 1) и подставляем в уравнение -2 x + 10 y - 8 z + 6 = 0
-2(7)+10(1)-8(1)+6=0
-6<>0
Точка 5 не лежит в плоскости.
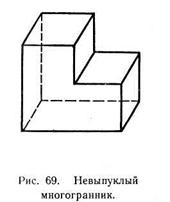
-Далее проверим многоугольник на выпуклость.
Одним из критериев выпуклости является следующее. Многоугольник будет выпуклым, если для векторов, составляющих его периметр, выполняется условие: векторные произведение соседних векторов должны иметь одинаковый знак.
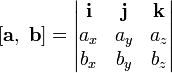
После последовательного выполнения векторного произведения, видим, что многоугольник выпуклый следовательно, данные 5 точек являются вершинами пирамиды с выпуклым основанием, вершины пирамиды:
(2,-1,-1)
(1, 2, 3)
(4, 1, 1)
(0, 1, 2)
(7, 1, 1)
(интерфейс программы)
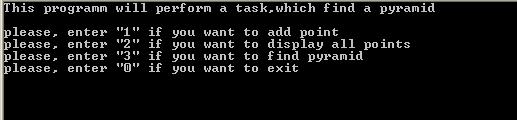
(ввод точек)
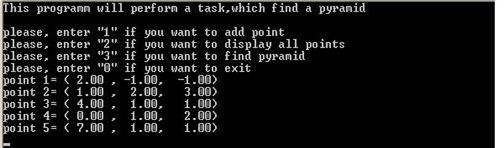
(вычисление вершин пирамиды с выпуклым основанием и вывод их на дисплей)
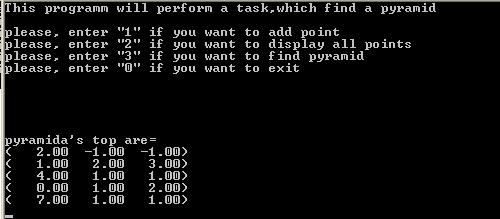
Заключение
пирамида вершина подпрограмма вектор
В курсовом проекте было предусмотрено следующее:
• создание библиотеки для работы с векторами в пространстве ;
• определение вершин пирамиды в с выпуклым основанием;
Список используемой литературы
1) Брусенцева В.С. Конспект лекций по программированию
2) Фаронов В. С. Turbo Pascal. Начальный курс. Учебное пособие. - М.: Нолидж»,1998 – 616 с.
3) Привалов И.И .Аналитическая геометрия. Учебник издательство «Лань» -304с .
4) Соболь Б.В. Практикум по высшей математике. издательство Ростов. 2006-640с
Приложение
Текст программ
Модуль MyUnit;
Unit MyUnitVector;
interface
Const {константы ошибок}
ListOk=0;
ListNotMem=1;
ListUnder=2;
ListEnd=3;
Type
mnoj=set of byte;
{Определение типов}
Coordinates=record {коориднаты}
x,y,z:real;
end;
P_Points=^point; {Описание типа Points}
point=record
data:Coordinates;
Next:P_Points;
end;
P_Descriptor=record {Дескриптор для работы со списком точек}
Start,Ptr:P_Points;
Number:Word;
end;
P_Vectors=^Vector; {Описание типа Vector}
Vector=record
data:Coordinates;
Next:P_Vectors;
end;
V_Descriptor=record {Дескриптор для работы со списком векторов}
V_Start,V_Ptr:P_Vectors;
V_Number:Word;
end;
Var
ListError:0..3; mno:mnoj;
{подпрограммы для формирования списка хранения и обработки списка векторов}
Procedure InitListOfVectors(var V:V_Descriptor);
Procedure PutVector(var V:V_Descriptor;c:Coordinates);
procedure CreateVector (a,b:Coordinates;var c:Coordinates);
Procedure WriteVectors(var V:V_Descriptor);
Procedure BeginOfVectors(var V:V_Descriptor);
{Подрограммы для работы с векторами}
Procedure AdditionVectors(a,b:Coordinates;var c:Coordinates);
Procedure MultOnNumber (Number:real; a:Coordinates;var c:Coordinates);
Function lengthOfVector(a:Coordinates):real;
Function Scalar(a,b:Coordinates):real;
Function angle(a,b:coordinates):real;
Function projection(a,b:coordinates):real;
Procedure VECTMult(a,b:Coordinates;var c:Coordinates);
Function collinearity(a,b:Coordinates):boolean;
Function MixeMult(a,b,c:Coordinates):real;
Function coplanarity(a,b,c:Coordinates):boolean;
{Подпрограммы для нахождения пирамиды в пространстве}
Procedure FinDaPyramid(var P:P_descriptor;mno:mnoj);
Procedure ploskost(var P:P_descriptor;a,b,c:coordinates;var ax,bx,cx,dx:real);
function proverka_na_ploskost(var P:P_descriptor;var mno:mnoj; n:byte):boolean;
Function Vypuklost(var P:P_descriptor;mno:mnoj;n:byte):boolean;
function Sign(T:real):byte;
{подпрограмм для формирования списка хранения и обработки точек}
Procedure InitListOfPoint(var P:P_Descriptor);
Procedure PutPoint(var P:P_Descriptor);
Procedure WritePoints(var P:P_Descriptor);
Procedure BeginOfPoints(var P:P_Descriptor);
Procedure ReadPoint(var P:P_Descriptor;var a:Coordinates);
Procedure MovePtrOfPoints(var P:P_Descriptor);
Procedure MoveToPoints(var P:P_Descriptor; n:word);
Procedure ClearMem(var P:P_Descriptor;var V:V_Descriptor);
Implementation
Procedure InitListOfVectors;
Begin
If MaxAvail<sizeOf(Vector) Then
ListError:=ListNotMem
else
begin
ListError:=ListOk;
V.V_Number:=0;
New(V.V_start);
V.V_Ptr:=V.V_Start;
end;
End;
Procedure PutVector;
var buf:P_Vectors;
Begin
If MaxAvail<sizeOf(Vector) Then
ListError:=ListNotMem
else
begin
ListError:=ListOk;
V.V_Ptr:=V.V_start;
New(Buf);
buf^.data:=c;
buf^.next:=V.V_Ptr^.next;
V.V_Ptr^.next:=buf;
V.V_Number:=V.V_number+1;
end;
end;
procedure createVector;
begin
with c do
begin
x:=a.x-b.x;
y:=a.y-b.y;
z:=a.z-b.z;
end;
end;
Procedure WriteVectors;
var index:word;
begin
If V.V_Number=0 then
ListError:=ListUnder
else
index:=1;
beginOfVectors(V);
while (V.V_Ptr^.next<>V.V_Start)and(index<=V.V_number) do
begin
writeln('Vector ',index,'= (',V.V_Ptr^.data.x:5:2,' , ',V.V_Ptr^.data.y:5:2,', ',V.V_Ptr^.data.z:5:2,') ');
V.V_Ptr:=V.V_Ptr^.next;
inc(index);
end;
end;
Procedure BeginOfVectors;
begin
V.V_Ptr:=V.V_start^.next;
end;
{Процедуры на свойства векторов}
Procedure AdditionVectors;
begin
with c do
begin
x:=a.x+b.x;
y:=a.y+b.y;
z:=a.z+b.z;
end;
end;
Procedure MultOnNumber;
begin
with c do
begin
x:=number*a.x;
y:=number*a.y;
z:=number*a.z;
end;
end;
Function lengthOfVector;
begin
lengthOfVector:=sqrt(sqr(a.x)+sqr(a.y)+sqr(a.z));
end;
Function Scalar;
begin
Scalar:=a.x*b.x+a.y*b.y+a.z*b.z;
end;
Function angle;
begin
Angle:= arccos(scalar(a,b))/(lengthOf Vector(a)*lengthOfVector(b));
end;
Function projection;
begin
projection:=(lengthOfVector(a)*lengthOfVector(b)*angle(a,b));
end;
Procedure VECTMult;
begin
with c do
begin
x:=a.y*b.z-b.y*a.z;
y:=a.z*b.x-b.z*a.z;
z:=a.x*b.y-b.x*a.y;
end;
end;
Function collinearity;
begin
if ((a.x/b.x)=(a.y/b.y))and((a.y/b.y)=(a.z/b.z)) then
collinearity:=true
else
collinearity:=false;
end;
Function MixeMult;
begin
MixeMult:=a.x*b.y*c.z+a.y*b.z*a.x+a.z*b.x*c.z-a.z*b.y*c.x-a.y*b.x*c.z-a.x*b.z*c.y;
end;
Function coplanarity;
begin
if MixeMult(a,b,c)=0 then
coplanarity:=true
else
coplanarity:=false; end;
{Подпрограммы для нахождения пирамиды}
Procedure ploskost;
var
j:word;
Begin
Ax:=(1*b.y*c.z)+(1*c.y*a.z)+(a.y*b.z*1)-(a.z*b.y*1)-(1*a.y*c.z)-(c.y*b.z*1);
Bx:=(a.x*1*c.z)+(1*b.z*c.x)+(b.x*1*a.z)-(a.z*1*c.x)-(b.x*1*c.z)-(1*b.z*a.x);
Cx:=(a.x*b.y*1)+(b.x*c.y*1)+(a.y*1*c.x)-(1*b.y*c.x)-(c.y*1*a.x)-(b.x*a.y*1);
Dx:=-((a.x*b.y*c.z)+(b.x*c.y*a.z)+(a.y*b.z*c.x)-(c.y*b.z*a.x)-(a.z*b.y*c.x)-(b.x*a.y*c.z));
if (ax=0)and(bx=0)and(cx=0) then
writeln('lejat na odnoi pr9mou');
end;
Procedure FindaPyramid;
var
i,k:word;
f,fl:boolean;
a:coordinates;
begin
mno:=[];
for i:=1 to p.number do
mno:=mno+[i];
f:=proverka_na_ploskost(p,mno,p.number);
if f then writeln('resheni9 net..vse to4ki lejat v ploskosti')
else
begin
i:=1;
fl:=false;
while (not fl)and(i<=p.number) do
begin
mno:=mno-[i];
writeln;
if proverka_na_ploskost(p,mno,p.number-1) then
fl:=Vypuklost(p,mno,p.number-1)
else
fl:=false;
mno:=mno+[i];
i:=i+1;
end;
if fl then
begin
writeln('pyramida''s top are= ');
for i:=1 to p.number do
begin
movetopoints(p,i);
readpoint(p,a);
Writeln('( ',a.x:6:2,' ',a.y:6:2,' ',a.z:6:2,') ');
end;
end
else writeln('pyramida is not found ');
end;
end;
function proverka_na_ploskost;
var
ax,bx,cx,dx:real;
i:word;
a,t1,t2,t3:coordinates;
f:boolean;
begin
i:=1;
while not( i in mno) do i:=i+1;
movetopoints(p,i);
readpoint(p,t1);
i:=i+1;
while not( i in mno) do i:=i+1;
movetopoints(p,i);
readpoint(p,t2);
i:=i+1;
while not( i in mno) do i:=i+1;
movetopoints(p,i);
readpoint(p,t3);
ploskost(p,t1,t2,t3,ax,bx,cx,dx);
f:=true;
while (i<=n)and f do
begin
i:=i+1;
while not( i in mno) do i:=i+1;
movetopoints(p,i);
readpoint(p,a);
if ax*a.x+bx*a.y+cx*a.z+dx=0 then
begin
f:=true;
end
else
begin
f:=false;
end;
end;
proverka_na_ploskost:=f;
end;
Function Vypuklost;
var
i,j,k:byte;
Q:boolean;
T,Z,Px:real;
a,b,v1,v2:coordinates;
begin
i:=1;
while not( i in mno) do i:=i+1;
movetopoints(p,i);
readpoint(p,a);
k:=0;
while (k<>n) do
begin
if (i in mno) then inc(k);
inc(i);
end;
movetopoints(p,i);
readpoint(p,b);
inc(i);
createVector(a,b,V1);
createVector(a,b,V2);
T:=(v1.y*v2.z-v2.y*v1.z)-(v1.x*v2.z-v2.y*v1.z)+(v1.x*v2.y-v2.x*v1.y);
Z:=Sign(T);
Px:=1.0;
j:=1;
Q:=true;
While (Q and (j<n))do
begin
while not( j in mno) do j:=j+1;
movetopoints(p,j);
readpoint(p,a);
inc(j);
while not( j in mno) do j:=j+1;
movetopoints(p,j);
readpoint(p,b);
createVector(a,b,V1);
createVector(a,b,V2);
T:=(v1.y*v2.z-v2.y*v1.z)-(v1.x*v2.z-v2.y*v1.z)+(v1.x*v2.y-v2.x*v1.y);
Px:=Px*Z*Sign(T);
if (Px<0) then Q:=false;
inc(i);
end;
Vypuklost:=Q;
end;
function Sign;
begin
if t=0 then
Sign:=1
else
sign:=round(t/abs(t));
end;
{Подпрограммы для обрабоки списка точек}
Procedure InitListOfPoint;
Begin
If MaxAvail<sizeOf(point) Then
ListError:=ListNotMem
else
begin
ListError:=ListOk;
P.Number:=0;
New(P.start);
P.Ptr:=P.Start;
end;
End;
Procedure PutPoint;
var buf:P_Points;
Begin
If MaxAvail<sizeOf(point) Then
ListError:=ListNotMem
else
begin
ListError:=ListOk;
P.ptr:=P.start;
New(Buf);
write('Input point = ');
readln(buf^.data.x,buf^.data.y,buf^.data.z);
buf^.next:=P.Ptr^.next;
P.Ptr^.next:=buf;
P.Number:=P.number+1;
end;
end;
Procedure WritePoints;
var index:word;
begin
If P.Number=0 then
ListError:=ListUnder
else
index:=1;
beginOfPoints(P);
while (P.Ptr^.next<>P.Start)and(index<=P.number) do
begin
writeln('point ',index,'= (',P.Ptr^.data.x:5:2,' , ',P.Ptr^.data.y:5:2,', ',P.Ptr^.data.z:5:2,') ');
P.Ptr:=P.Ptr^.next;
inc(index);
end;
end;
Procedure BeginOfPoints;
begin
P.Ptr:=P.start^.next;
end;
Procedure ReadPoint;
begin
if P.Number=0 then
ListError:=ListUnder
else
begin
ListError:=ListOk;
a:=P.Ptr^.data;
end;
end;
procedure MovePtrOfPoints;
begin
P.Ptr:=P.Ptr^.next;
end;
Procedure MoveToPoints;
var i:word;
begin
IF n>P.Number then
ListError:=ListUnder
else
begin
ListError:=ListOk;
P.Ptr:=P.start;
i:=0;
While i<n do
begin
P.Ptr:=P.Ptr^.next;
i:=i+1;
end;
end;
end;
Procedure ClearMem;
var
P_i,P_j:P_Points;
V_i,V_j:P_Vectors;
Begin
P_i:=P.start^.next;
V_i:=V.V_start^.next;
dispose(P.start);
dispose(V.V_start);
While (P.Number<>0) do
begin
P.Number:=P.number-1;
P_j:=P_i;
P_i:=P_i^.next;
dispose(P_j);
end;
dispose(V_j);
end;
end;
end.
Текст основной программы
program FindPyramid;
uses MyUnitVector,crt;
var D_Vector:V_Descriptor;
D_point :P_Descriptor;
a,b,c:Coordinates;
ch:char;
sum,sum2:real;
n1,n2:word;
begin
clrscr;
initlistOfPoint(D_point);
InitListOfVectors(D_vector);
repeat
writeln('This programm will perform a task,which find a pyramid ');
writeln;
writeln('please, enter "1" if you want to add point');
writeln('please, enter "2" if you want to display all points');
writeln('please, enter "3" if you want to find pyramid');
writeln('please, enter "0" if you want to exit');
ch:=readkey;
Case ch of
#49 : PutPoint(D_point);
#50 : begin
WritePoints(D_point);
readkey;
end;
#51 : begin
FinDaPyramid(D_point,mno);
readkey;
end;
end;
c lrscr;
until ch=#48;
clearmem(D_point,D_vector);
writeln('Error=',ListError);
readkey;
end.
 | |||
 | |||
Похожие работы
... не разработана. В следующей главе мы выявим особенности и методики применения основных идей квантового обучения в обучении математике. Глава 2. Особенности применения квантового обучения при обучении математике 2.1. Реализация основных идей квантового обучения в преподавании математики Рассмотрим реализацию основных идей квантового обучения в преподавании математике в соответствии с разбиением ...
... ' традиционные способы добычи пищи, ставили человека перед необходимостью радикально изменять обстоятельства жизнедеятельности, способствовали появлению культурных и социальных инноваций. Античная наука. 1.Возникновение письменности. Грандиозным по своей исторической значимости и последствиям событием было возникновение письменности. Письменность по сравнению с речью ...
... проходят крыловидные мышцы и верхнечелюстная артерия, лежит часть крыловидного венозного сплетения и зачелюстная вена. Через крыловидно-верхнечелюстную щель яма сообщается с крылонебной ямкой. Общая артрология и синдесмология В начале развития скелета зачатки костей связаны между собой мезенхимой непрерывно. Из нее возникает соединительная ткань, которая формирует два вида соединений – ...
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...


0 комментариев