Навигация
Max Z = – 5x1 + 2x2 + 0x3 + 0x4;
1. max Z = – 5x1 + 2x2 + 0x3 + 0x4;
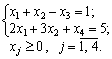
2. Векторна форма запису системи обмежень має вигляд:
![]() ,
,
де ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
У системі векторів для утворення початкового одиничного базису відсутній один вектор. Тому введемо штучну змінну в перше обмеження.
3. Розширена задача лінійного програмування буде такою:
maxZ = – 5x1 + 2x2 + 0x3 + 0x4 – Мx5;
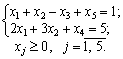
У цій задачі х4 та х5 – базисні змінні, а х1, х2, х3 – вільні. Нехай х1 = х2 = х3 = 0, тоді х4 = 5; х5 = 1.
Перший опорний план задачі:
X0 = (0; 0; 0; 5; 1), Z0 = – M.
З останньої симплекс-таблиці запишемо оптимальний план прямої задачі:
Х* = (0; 5/3; 2/3; 0), Zmax = 10/3.
Згідно зі співвідношенням двоїстості за першою теоремою можна висновувати, що оптимальний план двоїстої задачі існує і min F = max Z = 10/3.
Компоненти вектора Y* (оптимальний план двоїстої задачі) визначимо за формулою:
![]() ,
,
де ![]() та міститься в стовпчику «сбаз» останньої симплекс-таблиці;
та міститься в стовпчику «сбаз» останньої симплекс-таблиці;
![]() .
.
Матриця D– 1 також міститься в останній симплекс-таблиці у стовпчиках змінних «x5» та «x4», які утворювали початковий базис.
Отже,
![]() ,
,
min F = – 1 х 0 + 5 х 2/3 = 10/3.
Застосувавши для розв’язування прямої задачі симплекс-метод, ми знайшли її оптимальний план, а потім визначили оптимальний розв’язок двоїстої задачі за допомогою співвідношень першої теореми двоїстості.
До заданої задачі лінійного програмування записати двоїсту задачу. Розв’язавши двоїсту задачу графічно, визначити оптимальний план прямої задачі.
min Z = x1 + 2x2 + 2x3;
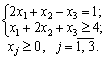
Розв’язання. За відповідними правилами побудуємо двоїсту задачу:
mах F = y1 + 4y2;
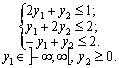
Зауважимо, що задачі несиметричні, і тому змінна у1, що відповідає першому рівнянню в системі обмежень прямої задачі, може мати будь-який знак, а змінна у2 – лише невід’ємна.
Двоїста задача має дві змінні, а отже, її можна розв’язати графічно (рис. 3.2).
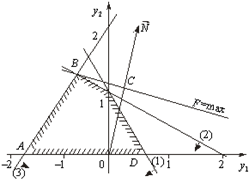
Рис. 3.2
Найбільшого значення цільова функція двоїстої задачі F досягає в точці В багатокутника ABCD. Її координати визначимо розв’язанням системи рівнянь:
![]()
Отже, Y* = (– 2/3; 4/3); mах F = 1 х (– 2/3) + 4 х 4/3 = 14/3.
Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості.
Підставимо Y* у систему обмежень двоїстої задачі і з’ясуємо, як виконуються обмеження цієї задачі:
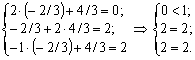
Оскільки перше обмеження для оптимального плану двоїстої задачі виконується як строга нерівність, то висновуємо, що перша змінна прямої задачі дорівнюватиме нулю х1 = 0 (перша частина другої теореми двоїстості).
Тепер проаналізуємо оптимальний план двоїстої задачі. Оскільки друга компонента плану у2 = 4/3 додатна, то друге обмеження прямої задачі для Х*виконуватиметься як строге рівняння (друга частина другої теореми двоїстості).
Об’єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій х1 = 0, та визначити решту змінних:
![]()
тобто Х* = (0; 5/3; 2/3), min Z = 1 х 0 + 2 х 5/3 + 2 х 2/3 = 14/3.
Умова min Z = max F = 14/3 виконується, і тому Х* = (0; 5/3; 2/3); Y* = (– 2/3; 4/3) є оптимальними планами відповідно прямої та двоїстої задач.
Визначити, чи є оптимальними такі плани сформульованої задачі лінійного програмування:
min Z = 12x1 – 4x2 + 2x3;
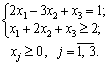
а) Х = (8/7; 3/7; 0); б) Х = (0; 1/5; 8/5); в) Х = (1/3; 0; 1/3).
Розв’язання. Принцип розв’язування задач такого типу ґрунтується на використанні другої теореми двоїстості. Необхідно побудувати двоїсту задачу та, допускаючи, що відповідний план Х є оптимальним, визначити оптимальний розв’язок двоїстої задачі. Якщо при цьому екстремальні значення цільових функцій будуть однаковими за величиною, то припущення правильне. Протилежне можна висновувати в таких випадках:
1. Якщо запропонований план Х недопустимий, тобто не задовольняє систему обмежень прямої задачі.
2. Якщо визначений план двоїстої задачі недопустимий, тобто не задовольняє всі обмеження двоїстої задачі.
3. Якщо визначений план двоїстої задачі допустимий, але для нього екстремальне значення цільової функції F не дорівнює значенню функції Z, тобто не виконується умова першої теореми двоїстості.
Запишемо двоїсту задачу до прямої задачі лінійного програмування:
max F = y1 + 2y2;
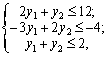
![]()
Перевіримо запропоновані плани на оптимальність.
1. Х = (8/7; 3/7; 0). Підставимо його в систему обмежень прямої задачі:
![]()
Обидва обмеження виконуються, і тому Х = (8/7; 3/7; 0) є допустимим планом прямої задачі. Припустимо тепер, що зазначений план є оптимальним планом прямої задачі. Тоді розрахуємо для нього величину цільової функції: Z = 12 х 8/7 – 4 х 3/7 + 2 х 0 = 12.
Скористаємося другою теоремою двоїстості та визначимо відповідний план двоїстої задачі. Оскільки x1 = 8/7 > 0; x2 = 3/7 > 0, то згідно з другою частиною другої теореми двоїстості можна записати перше та друге обмеження як рівняння і визначити у1 та у2:
![]()
Підставимо ці значення в третє обмеження системи двоїстої задачі:
![]() ;
;
![]() .
.
Для визначених значень у1 = 4; у2 = 4 це обмеження не виконується, і тому відповідний план у = (4; 4) є недопустимим планом двоїстої задачі. Внаслідок цього наше допущення, що Х = (8/7; 3/7; 0) є оптимальним планом прямої задачі, виявилося помилковим.
2. Х = (0; 1/5; 8/5). Підставимо цей план у систему обмежень прямої задачі:
![]()
План допустимий, і для нього Z = 12 х 0 – 4 х 1/5 + 2 х 8/5 = 12/5.
Визначимо відповідний план двоїстої задачі. Оскільки компоненти x2 та x3 додатні, то друге і третє обмеження двоїстої задачі можна записати як рівняння:
![]()
Перевіримо, чи виконується перше обмеження двоїстої задачі для визначених значень у1 та у2: 2 х 8/5 + 2/5 = 18/5 < 12. Отже, перше обмеження виконується, і тому у = (8/5; 2/5) є допустимим планом двоїстої задачі. Для нього
F = 8/5 + 2 х 2/5 = 12/5 = Z.
З огляду на викладене можна висновувати, що Y* = (8/5; 2/5) є оптимальним планом двоїстої задачі, а X* = (0; 1/5; 8/5) – оптимальним планом прямої задачі.
Наше припущення відносно запропонованого плану виявилося правильним.
3. Х = (1/3; 0; 1/3). Для цього плану обмеження прямої задачі виконуються так:
![]()
Оскільки Х = (1/3; 0; 1/3) є недопустимим планом, то він не може бути також оптимальним планом прямої задачі.
Отже, перевірка запропонованих планів на оптимальність дала такі результати: а) ні; б) так, Х* = (0; 1/5; 8/5), min Z = 12/5; в) ні.
Список використаних джерел
1. Абрамов Л.М., Капустин В.Ф. Математическое программирование. Л., Изд-во Ленинград. ун-та, 1976. – 184 с.
2. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высш. шк., 1985.
3. Ашманов С.А. Линейное программирование. – М.: Наука, 1981.
4. Белман Р. Динамическое программирование. – М.: Изд-во иностранной литературы, 1960.
5. Белман Р., Дрейфус С. Прикладные задачи динамического программирования. – М.: Наука, 1965.
6. Вагнер Г. Основы исследования операций. – Т. 1–3. – М.: Мир, 1972.
7. Вентцель Е.С. Исследование операций. М.: «Сов. радио», 1972. – 552 с.
8. Вентцель Е.С. Элементы динамического программирования. – М.: Наука, 1964.
9. Гольштейн Е.Г., Юдин Д.Б. Новые направления в линейном программировании. – М.: Советское радио, 1966.
10. Гольштейн Е.Г., Юдин Д.Б. Задачи линейного программирования транспортного типа. – М.: Наука, 1969.
11. Данциг Дж. Линейное программирование, его обобщение и приложения. – М.: Прогресс, 1966.
12. Зайченко Ю.П. Дослідження операцій: Підручник. – 4-те вид., перероб. і допов. – К., 2000. – 688 с.
13. Зангвилл У. Нелинейное программирование. Единый подход. М.: «Сов.радио», 1973. – 312 с.
14. Ермольев Ю.М., Ястремский А.И. Стохастические модели и методы в экономическом планировании. М.: Наука, 1979. – 249 с.
15. Ермольев Ю.М. Методы стохастического программирования. – М.: Наука, 1976.
16. Калихман И.Л. Сборник задач по математическому программированию. – М.: Высшая шк., 1975.
Похожие работы
ача має назву задачі безумовного програмування. У якості прикладів економічних проблем, які доцільно розв’язувати. використовуючи методи та моделі математичного програмування, розглянемо такі: Приклад 1. Задача про планування випуску продукції малого підприємства. Планується виробляти жіночі та чоловічі костюми. На жіночій костюм потрібно 1 м. шерсті, 2 м. шовку та 1 людино-тиждень працевитрат. ...
... і відношення в класі виникають на основі другорядних, часто педагогічне небезпечних форм спілкування. Отже оптимальна організація педагогічного спілкування в навчальному процесі - актуальна проблема сучасної школи. За визначенням О.О. Леонтьєва "... оптимальне педагогічне спілкування - це таке спілкування вчителя із школярами в процесі навчання, яке створює найкращі умови для розвитку мотивації ...
... ів є актуальною, оскільки на її основі реально можна розробити формувальні, розвивальні та оздоровчі структурні компоненти технологічних моделей у цілісній системі взаємодії соціальних інститутів суспільства у формуванні здорового способу життя дітей та підлітків. На основі інформації, яка отримана в результаті діагностики, реалізується методика розробки ефективних критеріїв оцінки інноваційних ...
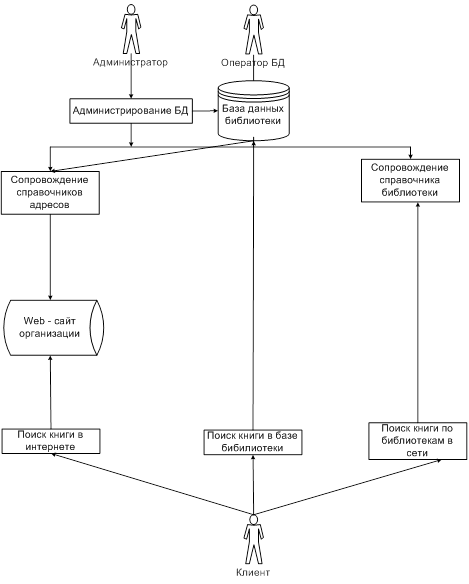
... адміністратор локальної мережі, який є у штатному розкладі і займається усіма проблемами, зв’язаними з комп’ютерами. Рисунок 1.2 – Функціональна схема автоматизованого робочого місця науково-технічної бібліотеки Метою розробки АРМ є - скорочення часу обробки оперативних даних, зменшення кількості помилок при обробці інформації. Основні функціональні вимоги до розроблюваного автоматизованого ...


0 комментариев