ЗАДАЧИ ОЧИСТКИ. ФИЗИКО-МЕХАНИЧЕСКИЕ СВОЙСТВА СЕМЯН

1 ЗАДАЧИ ОЧИСТКИ. ФИЗИКО-МЕХАНИЧЕСКИЕ СВОЙСТВА СЕМЯН

примесь семена очистка сортировка

Задачи очистки - выделение посторонних примесей из семян основной культуры. Выполняется она семяочистительными машинами. В основу работы отдельных органов машин положено использование различий в физико-механических свойствах семян основой культуры, семян и частиц засорителей .

Основными физико-механическими свойствами являются аэродинамические свойства, размеры, плотность, коэффициент трения, цвет, электрические свойства и др. На практике чаще всего используется аэродинамические свойства и три размерных показателя: толщина, ширина и длина.

2 ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ СВОЙСТВ СЕМЯН

Величина показателя любого из свойств семян изменяется в широких пределах в зависимости от культуры, сорта, спелости, влажности других факторов. Поэтому величину показателя можно считать случайной величиной. Для составления характеристик случайных величин используют методы математической статистики. Закономерность изменения физико-механических свойств семян может быть представлена математически законом нормального распределения. При котором плотность распределения вероятности характеризуется выражением:

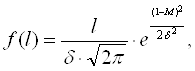(1)

где l – величина показателя данного свойства;

M – среднее математическое ожидание данного свойства;

δ – среднее квадратическое отклонение величины l от среднего значения M.

Значения M и δ определяются путем математической обработки достаточно большого количества замеров случайной величины. Методы определения значений M и δ изложены ниже.

Кривая распределения по нормальному закону имеет симметричный вид (рис.1). Максимальная ордината кривой, равная соответствует среднему значению признака l=M . По мере удаления от точки M плотность распределения падает и при l→±∞ кривая асимптотически приближается, а оси абсцисс.

Нормальный закон предусматривает изменение случайной величины от -∞ до +∞. Практически распределение укладывается в пределах отклонения от M на ±3δ.

За этими пределами распределения остается только 0,27% всех возможных значений случайной величины. Средняя величина M определяет положение кривой на оси абсцисс (рис.1), а среднее квадратическое отклонение характеризует форму кривой распределения, рассеивание величины показателя данного свойства семян около его среднего значения. Так как площадь под кривой всегда равна 1, то при увеличении δ кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс (кривая 1), при уменьшении δ кривая распределения поднимается вверх, одновременно, снижаясь с боков (кривая 3). Кривая 2 соответствует промежуточному значению между δ₁ и δ₂. Размерность δ совпадает с размерностью показателя l.

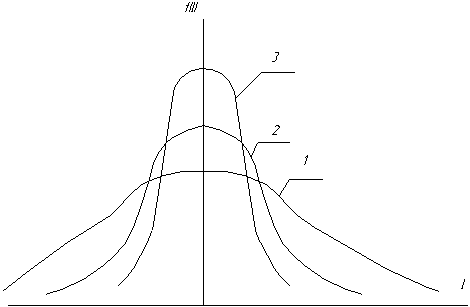
Рисунок 1. – Кривая распределения по нормальному закону.

3. РАСЧЁТ И ПОСТРОЕНИЕ ТЕОРЕТИЧЕСКИХ КРИВЫХ РАСПРЕДЕЛЕНИЯ СЕМЯН

При расчёте схем очистки семян от примесей характеристики физико-механических свойств семян представляют в виде кривых распределения, сопоставление которых позволяет составить технологическую схему очистки данного материала.

Для расчёта кривых распределений семян по какому-либо признаку используют уравнение (1) кривой нормального распределения. Для определения значений плотности f(l) заменяем переменную l на , тогда

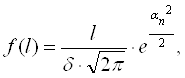(2)

Умножив обе части уравнения на δ, получим:

(3)

Значения функции  приведены в таблице. Разделив любое значение функции f(α_н) на δ, получим значение плотности f(α_н) .

4. ПОРЯДОК РАСЧЁТА И ПОСТРОЕНИЯ КРИВОЙ РАСПРЕДЕЛЕНИЯ

1) Построим кривую нормального распределения семян гречиха по толщине, если известно, что M=3,25 мм и δ=0,39.

Минимальная и максимальная толщина семян:

(4)

(5)

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 1.1).

Таблица 1.1- Расчёт значений f (l) гречиха

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	1,0228
0,75	0,3011	0,7721
1,50	0,1295	0,3321
2,25	0,0317	0,0813
3,00	0,0044	0,0113

Построим кривую нормального распределения семян овсюга по толщине, если известно, что M=2,10 мм и δ=0,30.

Минимальная и максимальная толщина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 1.2).

Таблица 1.2- Расчёт значений f (l) овсюга

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	1,3297
0,75	0,3011	1,0037
1,50	0,1295	0,4317
2,25	0,0317	0,1057
3,00	0,0044	0,0147

Построим кривую нормального распределения семян вика по толщине, если известно, что M=3,60 мм и δ=0,54.

Минимальная и максимальная толщина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 1.3).

Таблица 1.3- Расчёт значений f(l) вика

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	0,7387
0,75	0,3011	0,5576
1,50	0,1295	0,2398
2,25	0,0317	0,0587
3,00	0,0044	0,0081

Построим кривую нормального распределения семян щирица по толщине, если известно, что M=8,65 мм и δ=0,05.

Минимальная и максимальная толщина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 1.4).

Таблица 1.4- Расчёт значений f(l) щирица

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	7,9780
0,75	0,3011	6,0220
1,50	0,1295	2,5900
2,25	0,0317	0,6340
3,00	0,0044	0,0880

Построим кривую нормального распределения семян горец вьюнковый по толщине, если известно, что M=2,10 мм и δ=0,21.

Минимальная и максимальная толщина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 1.5).

Таблица 1.5- Расчёт значений f(l) горец вьюнковый

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	1,8995
0,75	0,3011	1,4338
1,50	0,1295	0,6167
2,25	0,0317	0,1510
3,00	0,0044	0,0210

При построении кривой плотности вероятности (кривой распределения) отмечаем на оси абцисс значения средней величины M. Вправо и влево от M откладываем по 3δ получаем на оси абцисс значения t_min и t_max.Разделим интервал от t_min до t_max на 8 равных частей, получаем на оси абцисс отметки, соответствующие отклонениям α_н от среднего значения M в обе стороны. Против M(отклонение α_н=0) откладывает отрезок , равный в принятом масштабе ординат значению плотности распределения f(l)= f()/δ , против отклонений 0,75δ, 1,5δ, 2,25δ, 3δ откладываем соответствующие им значения f(l). Полученные точки соединяем плавной кривой. Полученная кривая характеризует распределение семян по толщине.

Для расчёта схемы очистки необходимо построить кривые распределения семян основной культуры и примесей по аэродинамическим свойствам, толщине, ширине и длине семян.

2) Теперь построим кривую нормального распределения семян по ширине.

Построим кривую нормального распределения семян гречихи по ширине, если известно, что M=4,00 мм и δ=0,35.

Минимальная и максимальная ширина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 2.1).

Таблица 2.1- Расчёт значений f(l) гречиха

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	1,1397
0,75	0,3011	0,8603
1,50	0,1295	0,3700
2,25	0,0317	0,0906
3,00	0,0044	0,0126

Построим кривую нормального распределения семян овсюга по ширине, если известно, что M=2,30 мм и δ=0,35.

Минимальная и максимальная ширина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 2.2).

Таблица 2.2- Расчёт значений f(l) овсюг

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	1,1397
0,75	0,3011	0,8603
1,50	0,1295	0,3700
2,25	0,0317	0,0906
3,00	0,0044	0,0126

Построим кривую нормального распределения семян вика по ширине, если известно, что M=4,50 мм и δ=0,52.

Минимальная и максимальная ширина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 2.3).

Таблица 2.3- Расчёт значений f(l) вика

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	0,7671
0,75	0,3011	0,5790
1,50	0,1295	0,2490
2,25	0,0317	0,0610
3,00	0,0044	0,0085

Построим кривую нормального распределения семян щирица по ширине, если известно, что M=1,20 мм и δ=0,11.

Минимальная и максимальная ширина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 2.4).

Таблица 2.4- Расчёт значений f(l) щирица

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	3,6264
0,75	0,3011	2,7373
1,50	0,1295	1,1773
2,25	0,0317	0,2882
3,00	0,0044	0,0400

Построим кривую нормального распределения семян горец вьюнковый по ширине, если известно, что M=2,30 мм и δ=0,19.

Минимальная и максимальная ширина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 2.5).

Таблица 2.5- Расчёт значений f(l) горец вьюнковый

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	2,0995
0,75	0,3011	1,5847
1,50	0,1295	0,6816
2,25	0,0317	0,1668
3,00	0,0044	0,0232

3) Теперь построим кривую нормального распределения семян по длине.

Построим кривую нормального распределения семян гречихи по длине, если известно, что M=4,32 мм и δ=0,46.

Минимальная и максимальная длина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 3.1).

Таблица 3.1- Расчёт значений f(l) гречихи

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	0,8672
0,75	0,3011	0,6546
1,50	0,1295	0,2815
2,25	0,0317	0,0689
3,00	0,0044	0,0096

Построим кривую нормального распределения семян овсюга по длине, если известно, что M=12,00 мм и δ=1,32.

Минимальная и максимальная длина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 3.2).

Таблица 3.2- Расчёт значений f(l) овсюга

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	0,3022
0,75	0,3011	0,2281
1,50	0,1295	0,0981
2,25	0,0317	0,0240
3,00	0,0044	0,0033

Построим кривую нормального распределения семян вика по длине, если известно, что M=5,32 мм и δ=0,60.

Минимальная и максимальная длина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 3.3).

Таблица 3.3- Расчёт значений f(l) вика

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	0,6648
0,75	0,3011	0,5018
1,50	0,1295	0,2158
2,25	0,0317	0,0528
3,00	0,0044	0,0073

Построим кривую нормального распределения семян щирица по длине, если известно, что M=2,25 мм и δ=0,18.

Минимальная и максимальная длина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 3.4).

Таблица 3.4- Расчёт значений f(l) щирица

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	2,2161
0,75	0,3011	1,6728
1,50	0,1295	0,7194
2,25	0,0317	0,1761
3,00	0,0044	0,0244

Построим кривую нормального распределения семян горец вьюнковый по длине, если известно, что M=3,40 мм и δ=0,20.

Минимальная и максимальная длина семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 3.5).

Таблица 3.5- Расчёт значений f(l) горец вьюнковый

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	1,9945
0,75	0,3011	1,5055
1,50	0,1295	0,6475
2,25	0,0317	0,1585
3,00	0,0044	0,0220

4) При построении кривых распределения по аэродинамическим свойствам значения δ и M определяем по формулам:

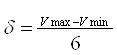и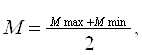

где – V_max и V_min соответственно, максимальная и минимальная скорость воздушного потока (из задания).

 

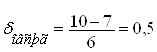
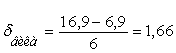
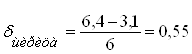
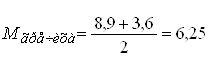
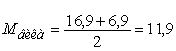
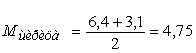
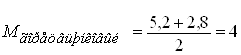
Результаты занесли в таблицу 4.1

Таблица 4.1- Расчёт значений δ и M

Культура	δ	M
Гречиха	0,88	6,25
Овсюг	0,5	8,5
Вика	1,66	11,9
Щирица	0,55	4,75
Горец вьюнковый	0,4	4

5) Построим кривую нормального распределения семян гречихи по аэродинамическим свойствам, если известно, что M=6,25 мм и δ=0,88.

Минимальная и максимальная толщина по аэродинамическим свойствам семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 5.1).

Таблица 5.1- Расчёт значений f(l) гречихи

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	0,4533
0,75	0,3011	0,3422
1,50	0,1295	0,1472
2,25	0,0317	0,0360
3,00	0,0044	0,0050

Построим кривую нормального распределения семян овсюга по аэродинамическим свойствам, если известно, что M=8,5 мм и δ=0,5.

Минимальная и максимальная по аэродинамическим свойствам семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 5.2).

Таблица 5.2- Расчёт значений f(l) овсюга

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	0,7978
0,75	0,3011	0,6022
1,50	0,1295	0,2590
2,25	0,0317	0,0634
3,00	0,0044	0,0088

Построим кривую нормального распределения семян вика по аэродинамическим свойствам, если известно, что M=11,9 мм и δ=1,66.

Минимальная и максимальная по аэродинамическим свойствам семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 5.3).

Таблица 5.3- Расчёт значений f(l) вика

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	0,2403
0,75	0,3011	0,1814
1,50	0,1295	0,0780
2,25	0,0317	0,0191
3,00	0,0044	0,0027

Построим кривую нормального распределения семян щирица по аэродинамическим свойствам, если известно, что M=4,75 мм и δ=0,55.

Минимальная и максимальная по аэродинамическим свойствам семян:

Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 5.4).

Таблица 5.4- Расчёт значений f(l) щирица

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	0,7253
0,75	0,3011	0,5475
1,50	0,1295	0,2355
2,25	0,0317	0,0576
3,00	0,0044	0,0080

Построим кривую нормального распределения семян горец вьюнковый по аэродинамическим свойствам, если известно, что M=4 мм и δ=0,4.

Минимальная и максимальная толщина семян:

 Составляем таблицу значений плотности вероятности для четырех  от среднего значения M(таблица 5.5).

Таблица 5.5- Расчёт значений f(l) горец вьюнковый

Отклонение	f()	f(l)= f()/δ
0,00	0,3989	0,9973
0,75	0,3011	0,7528
1,50	0,1295	0,3238
2,25	0,0317	0,0793
3,00	0,0044	0,0110

При расчёте результатов необходимо определить количество семян, у которых величина показателя физико-математических свойств ограничена определенными условиями (требования ГОСТа, потери семян в отходы или количество примесей в основном материале).

Примечание. Под кривой распределения любой культуры находится 10000 зёрен. (по 5000 штук влево и вправо от M). Это не зависит от процента семян в смеси.

РАСЧЁТ КОЛИЧЕСТВА СЕМЯН ПРИМЕСЕЙ, ВЫДЕЛЕННЫХ РАБОЧИМ ОРГАНОМ

Имеем культуру с параметрами M=3,6 мм и δ=0,54мм. Рассчитаем, сколько зерен находиться по толщине семян до размера t=1,98.

По формуле определяем

(6)

По таблице значений нормального интеграла находим значение α_н=3. α_н=3 соответствует 4987.Так как половина кривой распределения (M=3,6) соответствует 10000/2=5000 шт. зерен, то с толщиной 1,98 будет 5000-4987=13 зерен.

Аналогично для границы второго класса t₂=4,42 будем иметь

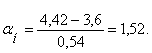
По таблице значений нормального интеграла находим значение α_н=1,50 соответствует 4332, а оставшиеся 0,02 умножаем на число в строке «дифференция для 0,01», что соответствует 2×12=24 шт. Таким образом, числу, α_н=1,52 соответствует нормальный интеграл Ф₂=4332+24=4356 шт.

Определяем количество зерен в классовом промежутке от 1,98 до 4,42 мм.

∆Ф=Ф₁-Ф₂= 13+4356=4369 зерен.

При определении количества зерен в классовом промежутке, включающем M, сначала находим количество зерен с левой стороны, затем с правой и суммируем результаты. Мы выделим 631 зерен из 10000.

 Из этого следует что 10000 – 3% 4356 –A% , тогда получаем

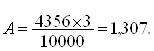
 Имеем культуру с параметрами M= 2,10 и δ=0,30. Рассчитаем, сколько зерен находиться по толщине семян до размера t=2,08.

По формуле определяем

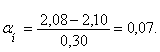
По таблице значений нормального интеграла находим значение α_н=0,05 соответствует 199, а оставшиеся 0,02 умножаем на число в строке «дифференция для 0,01», что соответствует 2×40=80 шт. Таким образом, числу, α_н=0,07 соответствует нормальный интеграл Ф₂=199+80=279 шт.

Определяем количество зерен.

∆Ф=Ф₁-Ф₂= 5000-279=4721 зерен.

При определении количества зерен в классовом промежутке, включающем M, сначала находим количество зерен с левой стороны, затем с правой и суммируем результаты. Мы выделим 4721 зерен из 10000.

 Из этого следует что 10000 – 2% 4721 –A% , тогда получаем

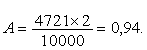
Имеем культуру с параметрами M= 2,10 и δ=0,21. Рассчитаем, сколько зерен находиться по толщине семян до размера t=2,08.

По формуле определяем

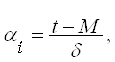
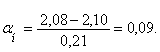
По таблице значений нормального интеграла находим значение α_н=0,05 соответствует 199, а оставшиеся 0,04 умножаем на число в строке «дифференция для 0,01», что соответствует 4×40=160 шт. Таким образом, числу, α_н=0,09 соответствует нормальный интеграл Ф₁=199+160=359 шт. Так как половина кривой распределения (M=2,10) соответствует 10000/2=5000 шт. зерен, то с толщиной 2,08 будет 5000-359=4641 зерен.

Определяем количество зерен.

∆Ф=Ф₁-Ф₂= 5000-359=4641 зерен.

При определении количества зерен в классовом промежутке, включающем M, сначала находим количество зерен с левой стороны, затем с правой и суммируем результаты. Мы выделим 6 зерен из 10000.

 Из этого следует что 10000 – 5% 4641 –A% , тогда получаем

Теперь подсчитаем технологический эффект разделения (E) по толщине.

Расчёты производим по следующей формуле

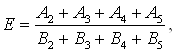(7)

где A₂ ,A₃ ,A₄ ,A₅ - процентное содержание семян сорняков, которое мы можем выделить из основной культуры, не теряя ее в отходы.

B₂ ,B₃ ,B₄ ,B₅ - процентное содержание примесей, которое было до разделения(дано из задания).

2) Имеем культуру с параметрами M=2,30 мм и δ=0,35 мм. Рассчитаем, сколько зерен находиться по ширине семян до размера t=1,25.

По формуле определяем

По таблице значений нормального интеграла находим значение α_н=3. α_н=3 соответствует 4987.Так как половина кривой распределения (M=2,30) соответствует 10000/2=5000 шт. зерен, то с толщиной 1,25 будет 5000-4987=13 зерен.

Аналогично для границы второго класса t₂=2,95 будем иметь

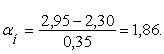
По таблице значений нормального интеграла находим значение α_н=1,85 соответствует 4678, а оставшиеся 0,01 умножаем на число в строке «дифференция для 0,01», что соответствует 1×7=7 шт. Таким образом, числу, α_н=1,86 соответствует нормальный интеграл Ф₂=4678+7=4685 шт. Так как половина кривой распределения (M=2,30) соответствует 10000/2=5000 шт. зерен, то с толщиной 2,95 будет 5000-4685=315 зерен.

Определяем количество зерен.

∆Ф=Ф₁-Ф₂= 5000+4685=9685 зерен.

При определении количества зерен в классовом промежутке, включающем M, сначала находим количество зерен с левой стороны, затем с правой и суммируем результаты. Мы выделим 9685 зерен из 10000.

Из этого следует что 10000 – 2% 9685 –A% , тогда получаем

Имеем культуру с параметрами M= 4,50 и δ=0,52.Рассчитаем, сколько зерен находиться по ширине семян до размера t=2,94.

По формуле определяем

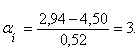
По таблице значений нормального интеграла находим значение α_н=3. α_н=3 соответствует 4987.Так как половина кривой распределения (M=4,50) соответствует 10000/2=5000 шт. зерен, то с толщиной 2,94 будет 5000-4987=13 зерен.

Аналогично для границы второго класса t₂=5,05 будем иметь

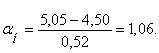
По таблице значений нормального интеграла находим значение α_н=1,05 соответствует 3531, а оставшиеся 0,01 умножаем на число в строке «дифференция для 0,01», что соответствует 1×22=22 шт. Таким образом, числу, α_н=1,06 соответствует нормальный интеграл Ф₂=3531+22=3553 шт. Так как половина кривой распределения (M=4,50) соответствует 10000/2=5000 шт. зерен, то с толщиной 5,05 будет 5000-3553=1447 зерен.

Определяем количество зерен в классовом промежутке от 2,94 до 5,05 мм.

∆Ф=Ф₁-Ф₂= 13+3553=3566 зерен.

При определении количества зерен в классовом промежутке, включающем M, сначала находим количество зерен с левой стороны, затем с правой и суммируем результаты. Мы выделим 3566 зерен из 10000.

Из этого следует что 10000 – 3% 3566 –A% , тогда получаем

Теперь подсчитаем технологический эффект разделения (E) по ширине семян.

Расчёты производим по следующей формуле

3) Имеем культуру с параметрами M=5,32 мм и δ=0,60 мм. Рассчитаем, сколько зерен находиться по длине семян до размера t=5, 7.

По формуле определяем

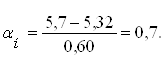
По таблице значений нормального интеграла находим значение α_н=0,7. α_н=0,7 соответствует 2580.Так как половина кривой распределения (M=2,91) соответствует 10000/2=5000 шт. зерен, то с толщиной 5,7 будет 5000-2580=2420 зерен.

Определяем количество зерен.

∆Ф=Ф₁-Ф₂= 5000-2580=2420 зерен.

При определении количества зерен в классовом промежутке, включающем M, сначала находим количество зерен с левой стороны, затем с правой и суммируем результаты. Мы выделим 2420 зерен из 10000.

 Из этого следует что 10000 – 3% 2420 –A% , тогда получаем

 Имеем культуру с параметрами M= 3,40 и δ=0,20.Рассчитаем, сколько зерен находиться по длине семян до размера t=2,94.

По формуле определяем

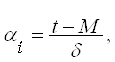
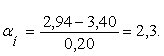
По таблице значений нормального интеграла находим значение α_н=2,3. α_н=2,3 соответствует 4946.Так как половина кривой распределения (M=3,40) соответствует 10000/2=5000 шт. зерен, то с толщиной 2,94 будет 5000-4946=54 зерен.

Определяем количество зерен.

∆Ф=Ф₁-Ф₂= 5000-4946=54 зерен.

При определении количества зерен в классовом промежутке, включающем M, сначала находим количество зерен с левой стороны, затем с правой и суммируем результаты. Мы выделим 54 зерен из 10000.

 Из этого следует что 10000 – 5% 54 –A% , тогда получаем

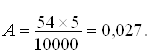
Теперь подсчитаем технологический эффект разделения (E) по длине семян.

Расчёты производим по следующей формуле

4) Имеем культуру с параметрами M=11,9 мм и δ=1,66 мм. Рассчитаем, сколько зерен находиться по аэродинамическим свойствам семян до размера t=8,89.

По формуле определяем

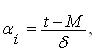
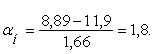
По таблице значений нормального интеграла находим значение α_н=1,8. α_н=1,8 соответствует 4641.Так как половина кривой распределения (M=11,9) соответствует 10000/2=5000 шт. зерен, то с толщиной 8,89 будет 5000-4641=359 зерно.

Определяем количество зерен.

∆Ф=Ф₁-Ф₂= 5000+4641=9641 зерен.

При определении количества зерен в классовом промежутке, включающем M, сначала находим количество зерен с левой стороны, затем с правой и суммируем результаты. Мы выделим 9641 зерен из 10000.

 Из этого следует что 10000 – 3% 9641 –A% , тогда получаем

 Имеем культуру с параметрами M= 8,5 и δ=0,50.Рассчитаем, сколько зерен находиться по аэродинамическим свойствам семян до размера t=8,89.

По формуле определяем

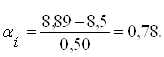
По таблице значений нормального интеграла находим значение α_н=0,7 соответствует 2580, а оставшиеся 0,08 умножаем на число в строке «дифференция для 0,01», что соответствует 8×31=248 шт. Таким образом, числу, α_н=0,78 соответствует нормальный интеграл Ф₁=2580+248=2828 шт. Так как половина кривой распределения (M=8,50) соответствует 10000/2=5000 шт. зерен, то с толщиной 8,89 будет 5000-2828=2172 зерен.

Определяем количество зерен.

∆Ф=Ф₁-Ф₂= 5000-2172=2828 зерен.

При определении количества зерен в классовом промежутке, включающем M, сначала находим количество зерен с левой стороны, затем с правой и суммируем результаты. Мы выделим 2828 зерен из 10000.

 Из этого следует что 10000 – 2% 2828 –A% , тогда получаем

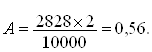
Имеем культуру с параметрами M= 4,75 и δ=0,55.Рассчитаем, сколько зерен находиться по аэродинамическим свойствам семян до размера t=3,61.

По формуле определяем

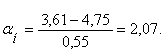
По таблице значений нормального интеграла находим значение α_н=2,0 соответствует 4773, а оставшиеся 0,07 умножаем на число в строке «дифференция для 0,01», что соответствует 7×5=35 шт. Таким образом, числу, α_н=2,07 соответствует нормальный интеграл Ф₁=4773+35=4808 шт. Так как половина кривой распределения (M=4,75) соответствует 10000/2=5000 шт. зерен, то с толщиной 3,61 будет 5000-4808=192 зерен.

Определяем количество зерен.

∆Ф=Ф₁-Ф₂= 5000-4808=192 зерен.

При определении количества зерен в классовом промежутке, включающем M, сначала находим количество зерен с левой стороны, затем с правой и суммируем результаты. Мы выделим 192 зерен из 10000.

 Из этого следует что 10000 – 5% 192 –A% , тогда получаем

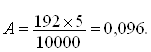
Имеем культуру с параметрами M= 4,0 и δ=0,40.Рассчитаем, сколько зерен находиться по аэродинамическим свойствам семян до размера t=3,61.

По формуле определяем

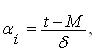
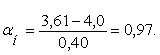
По таблице значений нормального интеграла находим значение α_н=0,95 соответствует 3289, а оставшиеся 0,02 умножаем на число в строке «дифференция для 0,01», что соответствует 2×25=50 шт. Таким образом, числу, α_н=0,97 соответствует нормальный интеграл Ф₁=3289+50=3339 шт. Так как половина кривой распределения (M=4,0) соответствует 10000/2=5000 шт. зерен, то с толщиной 3,61 будет 5000-3339=1661 зерен.

Определяем количество зерен.

∆Ф=Ф₁-Ф₂= 5000-1661=3339 зерен.

При определении количества зерен в классовом промежутке, включающем M, сначала находим количество зерен с левой стороны, затем с правой и суммируем результаты. Мы выделим 2828 зерен из 10000.

 Из этого следует что 10000 – 5% 3339 –A% , тогда получаем

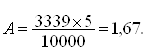
Теперь подсчитаем технологический эффект разделения (E) по длине семян.

Расчёты производим по следующей формуле

ЗАКЛЮЧЕНИЕ

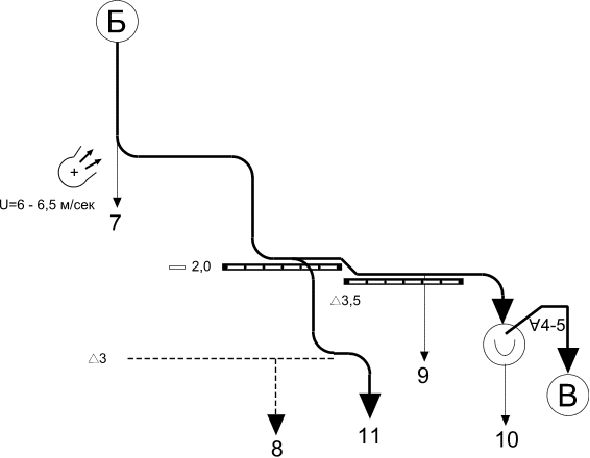
В данной курсовой работе была рассчитана схема технологического прочеса очистки семян по четырем различным признакам делимости, таким как толщина, ширина, длина и по аэродинамическим свойствам.

В расчетах основным показателем являлась эффективность очистки зерна основной культуры от примесей по четырем признакам делимости. Из расчетов можно сделать следующий вывод, что эффективность очистки семян наибольшая по такому признаку делимости как ширина. Эффективность в таком случае равна Е=0,87 , что лучше, чем эффективность по другим признакам делимости.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.  Бумбар И.В., Парубенко А.В., Конченко Н.Ф. Методические рекомендации для выполнения курсовой работы по теории сельскохозяйственных машин. – Благ.:ДальГАУ, 2004.

2.  Кленин Н.И., Сакун В.А. Сельскохозяйственные и мелиоративные машины. – М.: Колос, 1994.

3.  Халанский В.М., Горбачев И.В. Сельскохозяйственные машины. – М.: Колос, 2003.

4.  Кленин Н.И., Егоров В.Г. Сельскохозяйственные машины. – М.: Колос, 2003.