Навигация
1.2 Автоколебания
Системы автоматически регулирующие подачу энергии от внешнего источника, называются автоколебательными, а происходящие в них незатухающие периодические процессы - автоколебаниями. Такими системами являются часы, электрический звонок, ламповый генератор электромагнитных колебаний и т.д.
1.3 Разложение колебаний в гармонический спектр. Применение гармонического анализа для обработки диагностических данных
Сложение гармонических колебаний, направленных по одной прямой.
Возможны случаи, когда тело участвует одновременно в нескольких колебаниях, происходящих вдоль одного и того же или вдоль различных направлений.
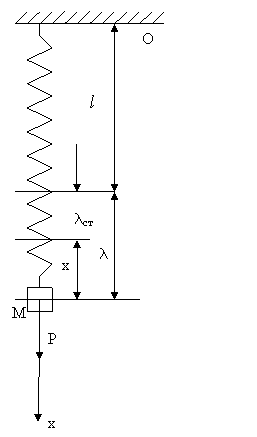
Рассмотрим сложение двух гармонических колебаний одинакового направления, одинаковой частоты и с одинаковыми амплитудами, но с разными начальными фазами a01 и a02. Смещение x колеблющегося тела будет суммой смещений x1 и x2:
x = x1 + x2 = Acos(w0t + a01) + Acos(w0t + a02).
Используя известную из тригонометрии формулу для суммы косинусов двух углов, ![]() имеем:
имеем:
![]()
Aрез![]() ,
,
то есть получается гармоническое колебание той же частоты с начальной фазой ![]() и амплитудой Aрез
и амплитудой Aрез![]() .
.![]()
Как видно, амплитуда Aрез результирующего колебания зависит от разности фаз складываемых колебаний.
Рассмотрим два крайних случая:
А) Колебания происходят в фазе, то есть a01 = a02, тогда ![]() и
и ![]() , поэтому Aрез = 2A.
, поэтому Aрез = 2A.
Если амплитуды не равны, Aрез = A1 + A2.
Б) Колебания происходят в противофазе, то есть a01 = a02 ± p, тогда ![]() . Следовательно, и Aрез = 0. Если амплитуды не равны, например, A1 > A2, то Aрез = A1 - A2.
. Следовательно, и Aрез = 0. Если амплитуды не равны, например, A1 > A2, то Aрез = A1 - A2.
Таким образом, при сложении двух одинаково направленных гармонических колебаний одного периода и с равными амплитудами получается гармоническое колебание того же периода с амплитудой, которая в зависимости от соотношения фаз складываемых колебаний может изменяться от удвоенного значения, если колебания происходят в фазе, до нуля, если они находятся в противофазе.
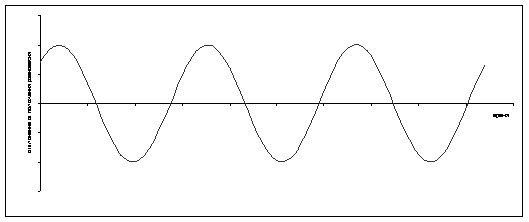
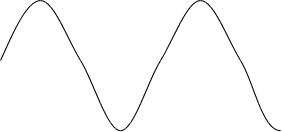
При сложении гармонических колебаний с разными частотами результирующее колебание не будет гармоническим, а будет являться сложным колебанием (Рис.4.).
|
| ||||
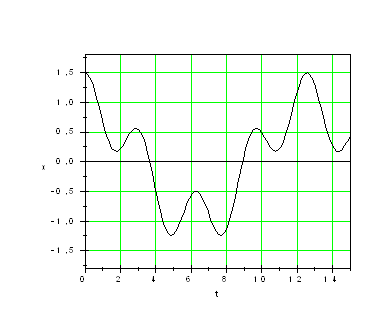
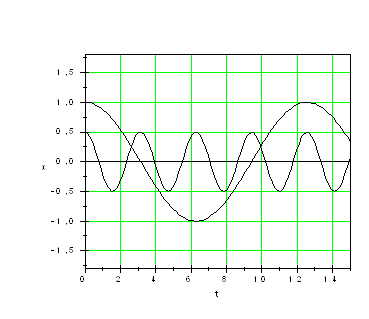
Рис. 4. Сложение гармонических колебаний с разными частотами:
А) исходные колебания, Б) результирующее колебание.
Сложное колебание и его гармонический спектр.
Согласно теореме Фурье, любое сложное колебание может быть представлено как сумма простых (гармонических) колебаний (гармоник), периоды или частоты которых кратны основному периоду или частоте сложного колебания.
Совокупность простых колебаний, на которые можно разложить данное сложное колебание, называется его гармоническим спектром.
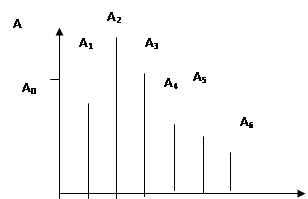
В гармоническом спектре сложного колебания указываются частоты и амплитуды всех составляющих его простых колебаний. Обычно спектр изображается в виде графика, на горизонтальной оси которого откладываются частоты; затем для каждой из частот простых колебаний имеющихся в спектре, строится ордината, соответствующая амплитуде этого колебания. Если гармонический спектр сложного колебания содержит только небольшое число простых колебаний и график его состоит из отдельных ординат, то такой спектр называется линейчатым (рис. 5.).
Если спектр содержит простые колебания практически всех частот в каких-то пределах, то он называется сплошным и график его строится в виде сплошной огибающей кривой.
Установление гармонического спектра является основным приемом при анализе сложного колебания. Этот анализ делается с помощью специальных приборов —гармонических анализаторов. Они применяются и в медицине при исследовании, например, колебаний биопотенциалов головного мозга и др. Многие процессы человеческого организма являются периодическими: сердечные сокращения, дыхание, кровенаполнение сосудов и т. п
 | |||||
| |||||
 | |||||
Сложение взаимно-перпендикулярных колебаний.
В результате сложения двух взаимно-перпендикулярных колебаний различного периода тело движется по сложным фигурам, форма которых зависит от соотношения периодов, амплитуд и начальных фаз складываемых колебаний и которые называются фигурами Лиссажу.
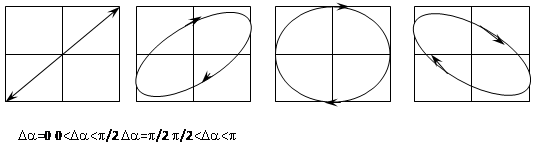
Рис. 6. Фигуры Лиссажу для колебаний различающихся начальными фазами Da.
Похожие работы
... уравнение в виде: или, обозначив с/m через k2, (1) Полученное уравнение определяет так называемые свободные колебания груза. Оно называется уравнением гармонического осциллятора. Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение: имеет мнимые корни , соответственно этому общее решение Для выяснения ...
... с использованием вновь изученного материала. 1.2 Развитие познавательного интереса к физике при использовании компьютерных технологий Глава 2 Компьютерное моделирование электромагнитных колебаний 2.1 Возможности применения графических пакетов при изучении электромагнитных колебаний в курсе физики средней школы На сегодняшний день разработано множество графических пакетов и оболочек (Соrel, ...
... интенсивностью волны. Таким образом, интенсивность сферической волны убывает обратно пропорционально квадрату расстояния от источника. 1 4 1 2 Применение.Областью применения колебаний и волн служат многие изобретения человека: от музыкальных инструментов и акустических динамиков до эхолотов и ультразвуковых диагностических аппаратов . С тремя последними мы и ...
... обнаруживает ряд выраженных частотных составляющих периодического характера, непосредственно связанных с основными движениями отдельных узлов и деталей исследуемой машины или механизма. Следовательно, частотный анализ дает возможность обнаружения отдельных источников механических колебаний. Количественная оценка амплитуд механических колебаний Для количественной оценки амплитуд механических ...
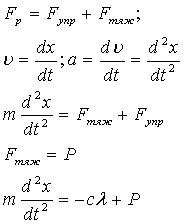

0 комментариев