Реферат Выполнил: студент гр. МХТ-02 Казаков Василий Васильевич
Магнитогорский государственный технический университет им. Г.И. Носова
Магнитогорск 2003
Колебаниями называются процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качания маятника часов, переменный электрический ток и т.д. При колебательном движении маятника изменяется координата центра масс, в случае переменного тока колеблются напряжение и сила тока. Физическая природа колебаний может быть разной, однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Рассмотрим механические колебания.
Гармонические колебания.Гармоническими колебаниями называются колебания, при которых изменяющаяся величина изменяется по закону синуса (косинуса).
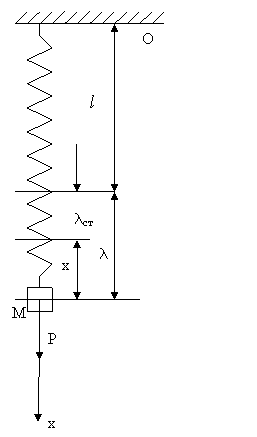
Пусть груз весом Р подвешен на вертикальной пружине, длина которой в естественном состоянии равна ![]() . Груз слегка оттянут книзу и затем отпущен. Найдем закон движения груза, пренебрегая массой пружины и сопротивлением воздуха.
. Груз слегка оттянут книзу и затем отпущен. Найдем закон движения груза, пренебрегая массой пружины и сопротивлением воздуха.
 Решение
Решение
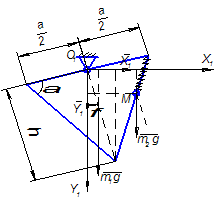
Направим ось Ох вниз по вертикальной прямой, проходящей через точку подвеса груза. Начало координат О выберем в положении равновесии груз, то есть в точке, в которой вес груза уравновешивается силой натяжения пружины.
![]() Пусть l означает удлинение пружины в данный момент, а lст—статическое удлинение, т.е. расстояние от конца нерастянутой пружины до положения равновесия. Тогда l=lст+х, или l-lст=х.
Пусть l означает удлинение пружины в данный момент, а lст—статическое удлинение, т.е. расстояние от конца нерастянутой пружины до положения равновесия. Тогда l=lст+х, или l-lст=х.
Дифференциальное уравнение получим из второго закона Ньютона: F=ma, где m=P/g—масса груза а—ускорение движения и F—равнодей-ствующая приложенных к грузу сил. В данном случае равнодействующая слагается из силы натяжения пружины и силы тяжести.
По закону Гука сила натяжения пружины пропорциональна её удлинению: Fупр=-сl, где с – постоянный коэффициент пропорциональности называемый жесткостью пружины.
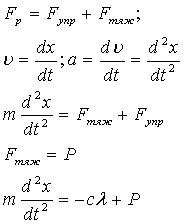
Так как в положении равновесия сила равновесия сила натяжения пружины уравновешивается весом тела, то P= сlст. Подставим в дифференциальное уравнение выражение Р и заменим l-lст через х, получится уравнение в виде:
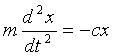
или, обозначив с/m через k2,
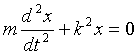 (1)
(1)
Полученное уравнение определяет так называемые свободные колебания груза. Оно называется уравнением гармонического осциллятора. Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение:
![]()
имеет мнимые корни ![]() , соответственно этому общее решение
, соответственно этому общее решение
![]()
Для выяснения физического смысла решения удобнее привести его к другой форме, введя новые произвольные постоянные. Умножив и разделив на ![]() , получим:
, получим:
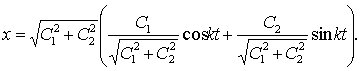
Если положить
![]()
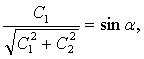
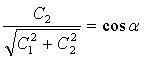
то
![]() (2)
(2)
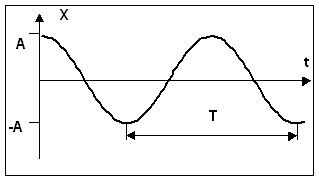
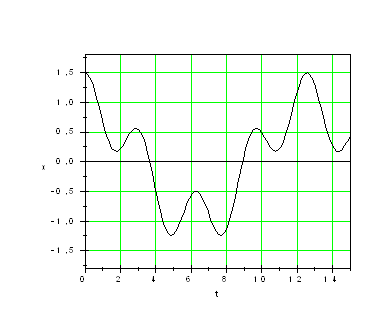
График гармонических колебаний имеет вид:
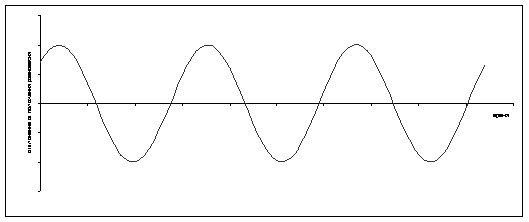
Таким образом, груз совершает гармонические колебания около положения равновесия.
Величину А называют амплитудой колебания, а аргумент ![]() — фазой колебания. Значение фазы при t=o т.e. величина
— фазой колебания. Значение фазы при t=o т.e. величина ![]() , называется начальной фазой колебания. Величина
, называется начальной фазой колебания. Величина ![]() есть частота колебания. Период колебания
есть частота колебания. Период колебания ![]() и частота k зависят только от жесткости пружины и от массы системы. Так как с = Р/lст = mg/lст, то для периода можно получить также формулу:
и частота k зависят только от жесткости пружины и от массы системы. Так как с = Р/lст = mg/lст, то для периода можно получить также формулу:
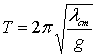
Скорость движения груза получается дифференцированием решения по t:
![]()
Для определения амплитуды и начальной фазы необходимо задать начальные условия. Пусть, например, в начальный момент t = 0 положение груза x=x0 и скорость u=u0. Тогда ![]()
![]() , откуда
, откуда
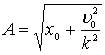 ,
, 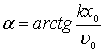
Из формул для амплитуды и начальной фазы видно, что в отличие от частоты и периода собственных колебаний они зависят от начального состояния системы. При отсутствии начальной скорости (u0=0) амплитуда А=х0, а начальная фаза a=p/2 и, таким образом,
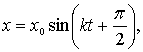 или
или ![]()
Затухающими колебаниями называются колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшают-ся. Найдем закон движения груза в условиях предыдущей задачи, но с учетом сопротивления воздуха, которое пропорционально скорости движения.
Решение
К силам, действующим на груз, прибавляется здесь сила сопротивления воздуха ![]() (знак минус показывает, что сила R направлена противоположно скорости u). Тогда дифференциальное уравнение движения в проекции на ось Ox имеет вид
(знак минус показывает, что сила R направлена противоположно скорости u). Тогда дифференциальное уравнение движения в проекции на ось Ox имеет вид
![]()
или если положить ![]() ,
, ![]() , то
, то
![]() (3)
(3)
Это уравнение также является линейным однородным уравнением второго порядка с постоянными коэффициентами. Его характеристическое уравнение:
![]()
имеет корни
![]() (4)
(4)
Характер движения целиком определяется этими корнями. Возможны три различных случая. Рассмотрим сначала случай, когда ![]() . Это неравенство имеет место, когда сопротивление среды невелико. Если положить
. Это неравенство имеет место, когда сопротивление среды невелико. Если положить ![]() , то корни (4) имеют вид
, то корни (4) имеют вид ![]() . Тогда общее решение можно записать в виде
. Тогда общее решение можно записать в виде
![]()
или, преобразовав, умножая и деля на ![]() , получим:
, получим:
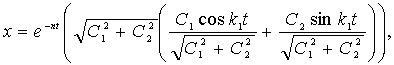
положим, что
![]()
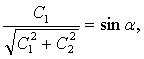
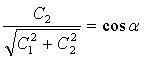 ,
,
тогда
![]() (5)
(5)
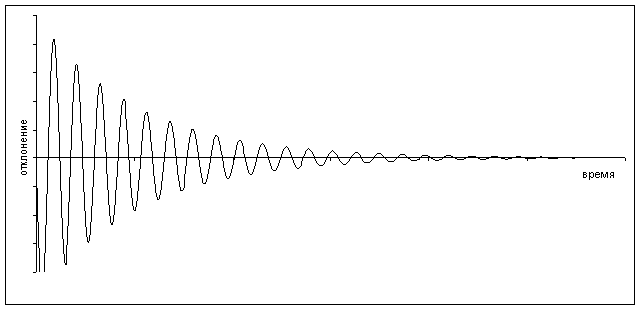
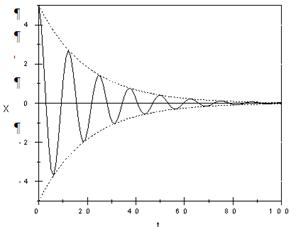
График зависимости отклонения от положения равновесия от времени имеет вид:
Если заданы начальные условия: ![]() при t = 0, то можно определить А и a. Для этого находим
при t = 0, то можно определить А и a. Для этого находим
![]()
и подставляем t = 0 в
выражения для ![]() и
и ![]() получим систему уравнений
получим систему уравнений
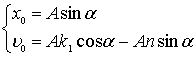
Разделелив обе части второго уравнения на соответствующие части первого получим
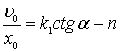
откуда
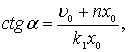 или
или 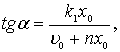 а
а 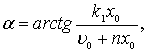
Так как
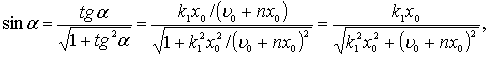
то
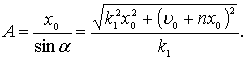
Решение (5) показывает, что имеют место затухающие колебания. Действии-тельно, амплитуда колебания ![]() зависит от времени и является монотонно убывающей функцией, причем
зависит от времени и является монотонно убывающей функцией, причем ![]() при
при ![]() .
.
Период затухающих колебаний определяется по формуле
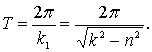
Моменты времени, в которые груз получает максимальное отклонение от начала координат (положения равновесия), образуют арифметическую прогрессию с разностью, равной полупериоду Т/2. Амплитуды затухающих колебаний образуют убывающую геометрическую прогрессию со знаменателем, равным ![]() или
или ![]() . Эта величина называется декрементом затухания и обычно обозначается буквой D. Натуральный логарифм декремента lnD = - пТ/2 называется логарифмическим декрементом затухания.
. Эта величина называется декрементом затухания и обычно обозначается буквой D. Натуральный логарифм декремента lnD = - пТ/2 называется логарифмическим декрементом затухания.
Частота колебаний ![]() в этом случае меньше, нежели в предыдущем (
в этом случае меньше, нежели в предыдущем (![]() ), но, как и там, не зависит от начального положения груза.
), но, как и там, не зависит от начального положения груза.
Если сопротивление среды велико и ![]() , то, положив
, то, положив ![]() , получим корни (4) в виде
, получим корни (4) в виде ![]() Так как
Так как ![]() , то оба корня отрицательны. Общее решение уравнения в этом случае имеет вид
, то оба корня отрицательны. Общее решение уравнения в этом случае имеет вид
![]() (6)
(6)
Отсюда видно, что движение апериодическое и не имеет колебательного характера. Аналогичный характер будет иметь движение и в случае ![]() , когда общее решение имеет вид
, когда общее решение имеет вид
![]() (7)
(7)
Легко заметить,
что в обоих последних
случаях при ![]() имеем
имеем ![]() .
.
Если заданы начальные условия ![]() и
и ![]() , то в случае, когда
, то в случае, когда ![]() , имеем
, имеем ![]() , а
, а ![]() . Решая эту систему относительно
. Решая эту систему относительно ![]() и
и ![]() , получим
, получим
![]() ,
, ![]()
и, следовательно
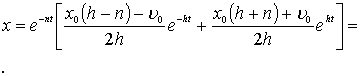
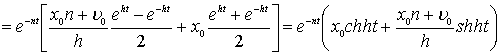
В случае же, когда ![]() , получаем
, получаем ![]() ,
, ![]() и следовательно,
и следовательно,
![]()
Вынужденными колебаниями называют колебания, вызванные внешней периодической возмущающей силой.
Пусть груз весом Р подвешен на вертикальной пружине, длина которой в ненагруженном состоянии равна ![]() . На груз действует периодическая возмущающая сила
. На груз действует периодическая возмущающая сила ![]() где Q и р — постоянные. Найдем закон движения груза, пренебрегая массой пружины и сопротивлением среды.
где Q и р — постоянные. Найдем закон движения груза, пренебрегая массой пружины и сопротивлением среды.
Решение
Как и для гармонических колебаний, получаем уравнение
![]()
Полагая, как и прежде, ![]() и, кроме того,
и, кроме того, ![]() перепишем уравнение в виде
перепишем уравнение в виде
![]() (8)
(8)
Это—неоднородное линейное уравнение второго порядка с постоянными коэффициентами, причем однородным уравнением, соответствующим уравнению (8), является (1). Поэтому ![]() ; остается найти х. Если предположить, что
; остается найти х. Если предположить, что ![]() , то частное решение х, нужно искать в виде
, то частное решение х, нужно искать в виде ![]() , где М и N — коэффициенты, подлежащие определению. Итак,
, где М и N — коэффициенты, подлежащие определению. Итак,
![]()
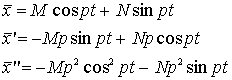
Производя вычисления, получаем
![]()
![]()
откуда М=0 и ![]() Полученное таким образом частное решение
Полученное таким образом частное решение
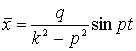 (9)
(9)
определяет так называемые вынужденные колебания, созданные возмущаю-щей силой ![]() . Вынужденные колебания, имеют тот же период, что и возмущающая сила, совпадают с ней по фазе (т. е. имеют одинаковую начальную фазу) при k>p, либо отличаются на p, если k<p, т. е. если N<0.
. Вынужденные колебания, имеют тот же период, что и возмущающая сила, совпадают с ней по фазе (т. е. имеют одинаковую начальную фазу) при k>p, либо отличаются на p, если k<p, т. е. если N<0.
Закон движения представляется общим решением
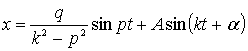 . (10)
. (10)
Оно слагается из собственно вынужденных колебаний (9), которые определяются внешней возмущающей силой, и собственных колебаний (2), обусловленных исключительно внутренними причинами: жесткостью пружины и массой груза.
Если заданы начальные условия: ![]() и
и ![]() , то можно определить произвольные постоянные А и u. Для этого продифференцируем функцию (10):
, то можно определить произвольные постоянные А и u. Для этого продифференцируем функцию (10):
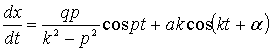
и подставим в выражения
х и ![]() значение
аргумента t = 0; получим систему уравнений
относительно A и a:
значение
аргумента t = 0; получим систему уравнений
относительно A и a:
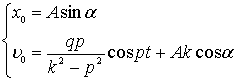
Преобразуем её так:
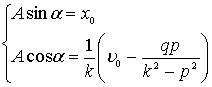
возведем в квадрат обе части каждого из этих уравнений и сложим. Тогда
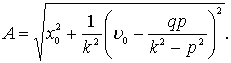
Для нахождения a разделим обе части первого уравнения на соответствую-щие части второго; получим
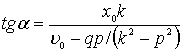
откуда
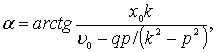
при этом ![]() ,
, 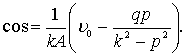
Итак, искомым частным решением, удовлетворяющим заданным начальным условиям, является функция
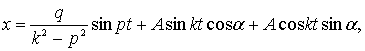
или
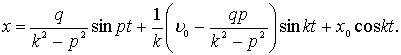
Частное решение (9), характеризующее собственно вынужденные колебания, было получено в предположении, что ![]() , т. е. что частота внешней силы не совпадает с частотой собственных колебаний. Если же
, т. е. что частота внешней силы не совпадает с частотой собственных колебаний. Если же ![]() , то дело будет обстоять совсем иначе. Действительно, уравнение (8) можно переписать теперь в виде
, то дело будет обстоять совсем иначе. Действительно, уравнение (8) можно переписать теперь в виде
![]() (11)
(11)
Частное решение следует искать в форме
![]() ,
,
где М и N — коэффициенты, подлежащие определению. Итак,
![]()
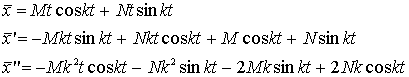
откуда получаем ![]() ,
, ![]() , и следовательно, частное решение имеет вид
, и следовательно, частное решение имеет вид
![]()
Общее решение в этом случае
![]() (12)
(12)
Найдем ![]() и подставим в выражения
х и
и подставим в выражения
х и ![]() значение t=0; получим
значение t=0; получим
![]()
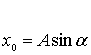
![]() или
или 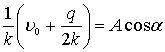
Из последних двух равенств находим
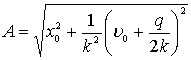 ,
, 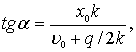
откуда
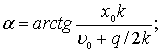
![]()
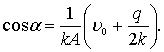
Перепишем общее решение так:
![]()
тогда искомое частное решение, удовлетворяющее заданным начальным условиям, запишется в виде.
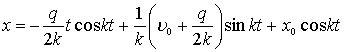
Выражение (12) показывает, что амплитуда вынужденных колебаний ![]() в этом случае может стать неограниченно большой даже тогда, когда q невелико. Иначе говоря, возможно получение сколь угодно больших амплитуд при малых возмущающих силах. Это явление называется резонансом. Таким образом, резонанс наступает тогда, когда частота возмущающей силы совпадает с частотой собственных колебаний.
в этом случае может стать неограниченно большой даже тогда, когда q невелико. Иначе говоря, возможно получение сколь угодно больших амплитуд при малых возмущающих силах. Это явление называется резонансом. Таким образом, резонанс наступает тогда, когда частота возмущающей силы совпадает с частотой собственных колебаний.
Впрочем, в действительности точное совпадение этих частот не является необходимым. Выражение (9) для вынужденного колебания показывает, что при близости частот амплитуда ![]() может быть очень большой, хотя и ограниченной при фиксированных частотах k и р. Возможностью создания колебаний с значительной амплитудой часто пользуются в различных усилителях, например в радиотехнике. С другой стороны, в большом числе случаев появление больших амплитуд является вредным, ибо может приводить к разрушению конструкций (скажем, мостов или перекрытий).
может быть очень большой, хотя и ограниченной при фиксированных частотах k и р. Возможностью создания колебаний с значительной амплитудой часто пользуются в различных усилителях, например в радиотехнике. С другой стороны, в большом числе случаев появление больших амплитуд является вредным, ибо может приводить к разрушению конструкций (скажем, мостов или перекрытий).
Найдем закон движения груза в условиях предыдущей задачи с учетом сопротивления среды, пропорционального скорости движения.
Решение
Как и выше, имеем
![]()
или положив![]() ,
, ![]() и
и ![]()
![]() (13)
(13)
Однородным уравнением, соответствующим (13), является уравнение (3) с корнями характеристического уравнения (4). Предположим, что сопротивление среды невелико, т. е. ![]() . При этом общее решение однородного уравнения имеет вид (5):
. При этом общее решение однородного уравнения имеет вид (5):
![]()
где ![]() . Это решение определяет свободные колебания, которые будут затухающими. Для отыскания вынужденных колебаний ищем частное решение в виде
. Это решение определяет свободные колебания, которые будут затухающими. Для отыскания вынужденных колебаний ищем частное решение в виде
![]()
Имеем:
![]()
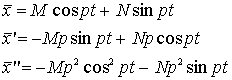
Сравнивая коэффициенты, получаем систему
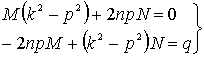
Так как
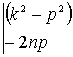
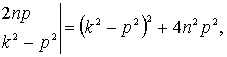
![]()
![]()
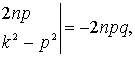
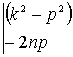
![]()
![]()
![]()
то
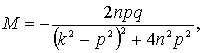 и
и 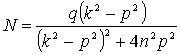
и мы находим частное решение
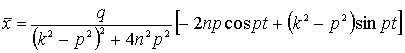
Преобразуем выражение ![]() следующим образом:
следующим образом: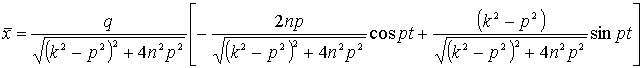 .
.
Обозначив
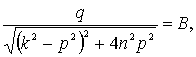
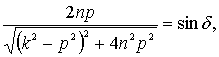
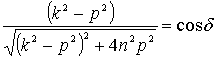 (14)
(14)
перепишем ![]() виде
виде
![]() (15)
(15)
Выражение
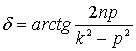 (16)
(16)
носит название сдвига фазы. Общее решение, как и в предыдущей задаче, слагается из свободных колебаний [см. формулу (5)] и собственно вынужденных колебаний (15):
![]() (17)
(17)
Первое слагаемое, как было сказано выше, определяет затухающие колебания, которые, особенно при большом ![]() , довольно скоро становятся мало ощутимыми. Что касается вынужденных колебаний (15), то их амплитуда (14) не зависит от времени и пропорциональна амплитуде Q периодического возмущения, так как
, довольно скоро становятся мало ощутимыми. Что касается вынужденных колебаний (15), то их амплитуда (14) не зависит от времени и пропорциональна амплитуде Q периодического возмущения, так как ![]() . Она отличается от q множителем
. Она отличается от q множителем
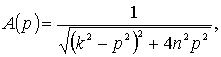 (18)
(18)
характеризующим зависимость амплитуды вынужденного колебания от частоты возмущающей силы.
Определим максимум этой амплитуды. Для этого найдем производную функции (18)
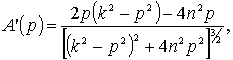
Положив ![]() , получим уравнение
, получим уравнение ![]() (случай р = 0
отбрасывается как невозможный),
корень которого дает частоту внешних сил:
(случай р = 0
отбрасывается как невозможный),
корень которого дает частоту внешних сил:
![]()
при которой, как показывает проверка достаточных условий экстремума, амплитуда вынужденных колебаний будет максимальной. Максимальное значение амплитуды равно
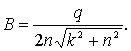 (19)
(19)
Формула (19) показывает, что амплитуда колебаний тем больше, чем меньше п. При малых п частота р близка к частоте собственных колебаний k.
Решение (15) существует всегда, когда
![]()
В случае ![]() получаем p=k и n= 0, и уравнение (13) превращается в уравнение (11). Здесь вновь наступает явление резонанса, при котором, как было рассмотрено выше, вынужденные колебания имеют вид (
получаем p=k и n= 0, и уравнение (13) превращается в уравнение (11). Здесь вновь наступает явление резонанса, при котором, как было рассмотрено выше, вынужденные колебания имеют вид (
Похожие работы
... При sin: B= При cos: A= Тогда Для имеем: Тогда общее решение дифференциального уравнения относительного движения шарика (1.1.3) принимает вид x= Скорость этого движения равна Составляющую реакции стенки трубки Nyопределим из второго уравнения системы (1.1.2) где определяется соответствующим выражением. 1.2 Закон изменения движущих сил, обеспечивающих ...
... период или частота, длина волны и форма колебаний) продольной волны, её уравнение и графику аналогичны поперечной. Рис. 7. График плоской волны 1.5 Энергетические характеристики волны механическое колебание гармонический спектр При волновом движении происходит перенос энергии, которая состоит из кинетической и потенциальной энергий колеблющихся частиц среды. Причем потенциальная энергия ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
... . , т.е. таких уравнений, у которых правая часть не является ненпрерывной по x функций рассмотрены в статье [5]. Теория систем автоматического управления, описываемых дифференциальными уравнениями с разрывными правыми частями рассматривается в книгах [13, 14, 15]. В работе С.В. Емельянова [13] излагается один из разделов теории автоматичесеого управления – теория систем с переменной структурой, ...

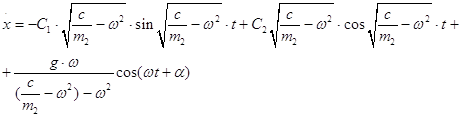




0 комментариев