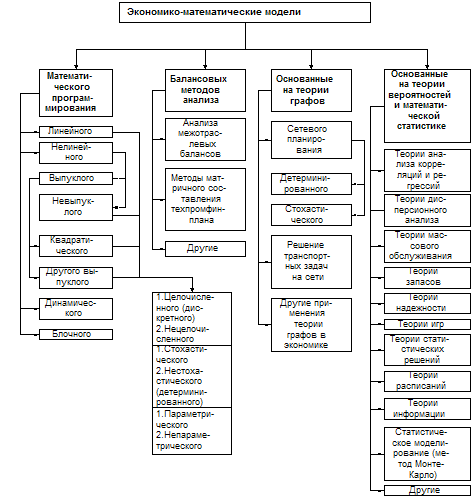
Навигация
Расчет оценок сезонной компоненты в мультипликативной модели
1. Расчет оценок сезонной компоненты в мультипликативной модели
Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние. Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый месяц (по всем годам) оценки сезонной компоненты Sj. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле, т.е. двенадцати, так как в нашем случае число периодов одного цикла (год) равно 12 месяцам. Для данной модели имеем:
![]() .
.
Определим корректирующий коэффициент:
![]() .
.
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом k:
![]() ,
,
где ![]() .
.
Проверим условие равенства двенадцати суммы значений сезонной компоненты:
![]() .
.
Таким образом, получены следующие значения сезонной компоненты:
Элиминируем влияние сезонной компоненты, разделив значение каждого уровня исходного временного ряда на соответствующие значения сезонной компоненты. Получим T∙E=Y/S, значения, которые содержат только тенденцию и случайную компоненту.
Таблица 5.3 Расчет выравненных значений Т и ошибок Е в мультипликативной модели
| t | y | S | y/S | T | T·S |
| E |
|
|
| 1 | 472,5 | 1,045 | 452,024 | 462,884 | 483,852 | 1223,600 | 0,977 | -11,352 | 128,866 |
| 2 | 482,1 | 0,992 | 486,039 | 464,396 | 460,632 | 644,144 | 1,047 | 21,468 | 460,863 |
| 3 | 489,5 | 0,995 | 492,032 | 465,908 | 463,510 | 323,280 | 1,056 | 25,990 | 675,460 |
| 4 | 493,6 | 0,994 | 496,428 | 467,419 | 464,757 | 192,654 | 1,062 | 28,843 | 831,923 |
| 5 | 488 | 0,996 | 490,190 | 468,931 | 466,836 | 379,470 | 1,045 | 21,164 | 447,915 |
| 6 | 490,6 | 0,993 | 494,071 | 470,443 | 467,138 | 284,934 | 1,050 | 23,462 | 550,462 |
| 7 | 492,5 | 1,000 | 492,362 | 471,955 | 472,087 | 224,400 | 1,043 | 20,413 | 416,700 |
| 8 | 488,1 | 0,997 | 489,587 | 473,466 | 472,028 | 375,584 | 1,034 | 16,072 | 258,315 |
| 9 | 493,1 | 1,000 | 493,166 | 474,978 | 474,915 | 206,784 | 1,038 | 18,185 | 330,712 |
| 10 | 484,5 | 0,997 | 485,935 | 476,490 | 475,083 | 528,080 | 1,020 | 9,417 | 88,688 |
| 11 | 483 | 0,997 | 484,563 | 478,001 | 476,459 | 599,270 | 1,014 | 6,541 | 42,783 |
| 12 | 476,9 | 0,994 | 479,676 | 479,513 | 476,738 | 935,136 | 1,000 | 0,162 | 0,026 |
| 13 | 477,9 | 1,045 | 457,190 | 481,025 | 502,814 | 874,976 | 0,950 | -24,914 | 620,722 |
| 14 | 467,5 | 0,992 | 471,320 | 482,537 | 478,626 | 1598,400 | 0,977 | -11,126 | 123,785 |
| 15 | 470,9 | 0,995 | 473,336 | 484,048 | 481,558 | 1338,096 | 0,978 | -10,658 | 113,586 |
| 16 | 469,1 | 0,994 | 471,787 | 485,560 | 482,794 | 1473,024 | 0,972 | -13,694 | 187,532 |
| 17 | 478,1 | 0,996 | 480,246 | 487,072 | 484,896 | 863,184 | 0,986 | -6,796 | 46,180 |
| 18 | 480,6 | 0,993 | 484,000 | 488,584 | 485,151 | 722,534 | 0,991 | -4,551 | 20,714 |
| 19 | 479,3 | 1,000 | 479,166 | 490,095 | 490,233 | 794,112 | 0,978 | -10,933 | 119,520 |
| 20 | 484,2 | 0,997 | 485,676 | 491,607 | 490,113 | 541,958 | 0,988 | -5,913 | 34,968 |
| 21 | 484,9 | 1,000 | 484,965 | 493,119 | 493,053 | 509,856 | 0,983 | -8,153 | 66,467 |
| 22 | 485,6 | 0,997 | 487,038 | 494,630 | 493,170 | 478,734 | 0,985 | -7,570 | 57,300 |
| 23 | 486,1 | 0,997 | 487,674 | 496,142 | 494,541 | 457,104 | 0,983 | -8,441 | 71,255 |
| 24 | 484,7 | 0,994 | 487,521 | 497,654 | 494,774 | 518,928 | 0,980 | -10,074 | 101,480 |
| 25 | 510,9 | 1,045 | 488,760 | 499,166 | 521,777 | 11,696 | 0,979 | -10,877 | 118,302 |
| 26 | 484,7 | 0,992 | 488,660 | 500,677 | 496,620 | 518,928 | 0,976 | -11,920 | 142,075 |
| 27 | 486,6 | 0,995 | 489,117 | 502,189 | 499,605 | 435,974 | 0,974 | -13,005 | 169,130 |
| 28 | 488,4 | 0,994 | 491,198 | 503,701 | 500,832 | 364,046 | 0,975 | -12,432 | 154,543 |
| 29 | 489,5 | 0,996 | 491,697 | 505,212 | 502,955 | 323,280 | 0,973 | -13,455 | 181,042 |
| 30 | 486,6 | 0,993 | 490,042 | 506,724 | 503,164 | 435,974 | 0,967 | -16,564 | 274,382 |
| 31 | 491,8 | 1,000 | 491,662 | 508,236 | 508,378 | 245,862 | 0,967 | -16,578 | 274,837 |
| 32 | 495,2 | 0,997 | 496,709 | 509,748 | 508,199 | 150,798 | 0,974 | -12,999 | 168,971 |
| 33 | 491,8 | 1,000 | 491,866 | 511,259 | 511,191 | 245,862 | 0,962 | -19,391 | 376,008 |
| 34 | 496,1 | 0,997 | 497,569 | 512,771 | 511,257 | 129,504 | 0,970 | -15,157 | 229,726 |
| 35 | 498,8 | 0,997 | 500,415 | 514,283 | 512,623 | 75,342 | 0,973 | -13,823 | 191,086 |
| 36 | 501,5 | 0,994 | 504,419 | 515,794 | 512,809 | 35,760 | 0,978 | -11,309 | 127,902 |
| 37 | 541 | 1,045 | 517,556 | 517,306 | 540,739 | 1123,590 | 1,000 | 0,261 | 0,068 |
| 38 | 512,3 | 0,992 | 516,486 | 518,818 | 514,613 | 23,232 | 0,996 | -2,313 | 5,351 |
| 39 | 512,6 | 0,995 | 515,251 | 520,330 | 517,652 | 26,214 | 0,990 | -5,052 | 25,526 |
| 40 | 511,5 | 0,994 | 514,430 | 521,841 | 518,869 | 16,160 | 0,986 | -7,369 | 54,300 |
| 41 | 511,9 | 0,996 | 514,197 | 523,353 | 521,015 | 19,536 | 0,983 | -9,115 | 83,079 |
| 42 | 513,9 | 0,993 | 517,536 | 524,865 | 521,178 | 41,216 | 0,986 | -7,278 | 52,965 |
| 43 | 520 | 1,000 | 519,854 | 526,376 | 526,524 | 156,750 | 0,988 | -6,524 | 42,562 |
| 44 | 515,9 | 0,997 | 517,472 | 527,888 | 526,284 | 70,896 | 0,980 | -10,384 | 107,836 |
| 45 | 524,2 | 1,000 | 524,270 | 529,400 | 529,329 | 279,558 | 0,990 | -5,129 | 26,308 |
| 46 | 527,1 | 0,997 | 528,661 | 530,912 | 529,344 | 384,944 | 0,996 | -2,244 | 5,035 |
| 47 | 529,8 | 0,997 | 531,515 | 532,423 | 530,705 | 498,182 | 0,998 | -0,905 | 0,820 |
| 48 | 534,9 | 0,994 | 538,014 | 533,935 | 530,845 | 751,856 | 1,008 | 4,055 | 16,443 |
| 49 | 578,2 | 1,045 | 553,144 | 535,447 | 559,701 | 5001,318 | 1,033 | 18,499 | 342,198 |
| 50 | 539,4 | 0,992 | 543,807 | 536,959 | 532,607 | 1018,886 | 1,013 | 6,793 | 46,148 |
| 51 | 545,3 | 0,995 | 548,120 | 538,470 | 535,700 | 1430,352 | 1,018 | 9,600 | 92,168 |
| 52 | 551,9 | 0,994 | 555,062 | 539,982 | 536,906 | 1973,136 | 1,028 | 14,994 | 224,816 |
| 53 | 549,7 | 0,996 | 552,167 | 541,494 | 539,074 | 1782,528 | 1,020 | 10,626 | 112,904 |
| 54 | 550,1 | 0,993 | 553,992 | 543,005 | 539,191 | 1816,464 | 1,020 | 10,909 | 119,009 |
| 55 | 554 | 1,000 | 553,845 | 544,517 | 544,670 | 2164,110 | 1,017 | 9,330 | 87,055 |
| 56 | 550 | 0,997 | 551,676 | 546,029 | 544,370 | 1807,950 | 1,010 | 5,630 | 31,698 |
| 57 | 565,6 | 1,000 | 565,676 | 547,541 | 547,467 | 3377,934 | 1,033 | 18,133 | 328,793 |
| 58 | 564,7 | 0,997 | 566,373 | 549,052 | 547,431 | 3274,128 | 1,032 | 17,269 | 298,224 |
| 59 | 566,9 | 0,997 | 568,735 | 550,564 | 548,788 | 3530,736 | 1,033 | 18,112 | 328,060 |
| 60 | 572,7 | 0,994 | 576,034 | 552,076 | 548,881 | 4253,648 | 1,043 | 23,819 | 567,361 |
| Итого | 52661,016 | 60,006 | 1,751 | 11202,95 |
Определим компоненту Т данной модели. Для этого проведем аналитическое выравнивание ряда (T∙E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
Таким образом, имеем линейный тренд:
![]() .
.
Подставив в это уравнение значение t = 1, 2, …, 60, найдем уровни Т для каждого момента времени.
Найдем значения уровней ряда, полученные по мультипликативной модели, умножив уровни Т на значения сезонной компоненты для соответствующих месяцев.
Расчет ошибки в мультипликативной модели проводится по формуле:
![]() .
.
Численные значения ошибок приведены в таблице
Для оценки качества построения мультипликативной модели можно использовать сумму квадратов абсолютных ошибок![]() . Для данной мультипликативной модели сумма квадратов абсолютных ошибок равна 11202,95. По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня, равной 52661,016, эта величина составляет 21,2%:
. Для данной мультипликативной модели сумма квадратов абсолютных ошибок равна 11202,95. По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня, равной 52661,016, эта величина составляет 21,2%:
![]() .
.
Следовательно, можно сказать, что мультипликативная модель объясняет 78,8% общей вариации уровней временного ряда объема продаж в перерабатывающей промышленности и торговле США за последние 60 месяцев. Мультипликативная модель построена.
При этом при расчете коэффициента автокорреляции первого порядка параметрами будут являться значения исходного ряда ![]() и значения ряда с отставанием на 1
и значения ряда с отставанием на 1 ![]() .
.
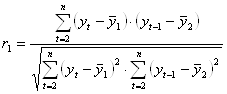
 ;
; 
Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков.
Таблица 5.4 Расчет коэффициента автокорреляции первого порядка
| t | y |
|
|
|
|
|
|
| 1 | 472,5 | - | - | - | - | - | - |
| 2 | 482,1 | 472,5 | -25,9729 | -33,8746 | 879,8204 | 674,5906 | 1147,4869 |
| 3 | 489,5 | 482,1 | -18,5729 | -24,2746 | 450,8488 | 344,9519 | 589,2551 |
| 4 | 493,6 | 489,5 | -14,4729 | -16,8746 | 244,2237 | 209,4643 | 284,7513 |
| 5 | 488 | 493,6 | -20,0729 | -12,7746 | 256,4226 | 402,9206 | 163,1898 |
| 6 | 490,6 | 488 | -17,4729 | -18,3746 | 321,0568 | 305,3016 | 337,6251 |
| 7 | 492,5 | 490,6 | -15,5729 | -15,7746 | 245,6556 | 242,5146 | 248,8373 |
| 8 | 488,1 | 492,5 | -19,9729 | -13,8746 | 277,1153 | 398,9160 | 192,5039 |
| 9 | 493,1 | 488,1 | -14,9729 | -18,2746 | 273,6231 | 224,1872 | 333,9601 |
| 10 | 484,5 | 493,1 | -23,5729 | -13,2746 | 312,9200 | 555,6807 | 176,2144 |
| 11 | 483 | 484,5 | -25,0729 | -21,8746 | 548,4587 | 628,6494 | 478,4971 |
| 12 | 476,9 | 483 | -31,1729 | -23,3746 | 728,6529 | 971,7485 | 546,3708 |
| 13 | 477,9 | 476,9 | -30,1729 | -29,4746 | 889,3329 | 910,4028 | 868,7506 |
| 14 | 467,5 | 477,9 | -40,5729 | -28,4746 | 1155,2956 | 1646,1587 | 810,8015 |
| 15 | 470,9 | 467,5 | -37,1729 | -38,8746 | 1445,0800 | 1381,8231 | 1511,2327 |
| 16 | 469,1 | 470,9 | -38,9729 | -35,4746 | 1382,5465 | 1518,8855 | 1258,4456 |
| 17 | 478,1 | 469,1 | -29,9729 | -37,2746 | 1117,2265 | 898,3736 | 1389,3940 |
| 18 | 480,6 | 478,1 | -27,4729 | -28,2746 | 776,7841 | 754,7592 | 799,4517 |
| 19 | 479,3 | 480,6 | -28,7729 | -25,7746 | 741,6088 | 827,8787 | 664,3288 |
| 20 | 484,2 | 479,3 | -23,8729 | -27,0746 | 646,3481 | 569,9145 | 733,0327 |
| 21 | 484,9 | 484,2 | -23,1729 | -22,1746 | 513,8488 | 536,9824 | 491,7118 |
| 22 | 485,6 | 484,9 | -22,4729 | -21,4746 | 482,5956 | 505,0304 | 461,1574 |
| 23 | 486,1 | 485,6 | -21,9729 | -20,7746 | 456,4773 | 482,8075 | 431,5830 |
| 24 | 484,7 | 486,1 | -23,3729 | -20,2746 | 473,8753 | 546,2916 | 411,0584 |
| 25 | 510,9 | 484,7 | 2,8271 | -21,6746 | -61,2766 | 7,9926 | 469,7873 |
| 26 | 484,7 | 510,9 | -23,3729 | 4,5254 | -105,7722 | 546,2916 | 20,4795 |
| 27 | 486,6 | 484,7 | -21,4729 | -21,6746 | 465,4156 | 461,0846 | 469,7873 |
| 28 | 488,4 | 486,6 | -19,6729 | -19,7746 | 389,0229 | 387,0223 | 391,0339 |
| 29 | 489,5 | 488,4 | -18,5729 | -17,9746 | 333,8397 | 344,9519 | 323,0854 |
| 30 | 486,6 | 489,5 | -21,4729 | -16,8746 | 362,3458 | 461,0846 | 284,7513 |
| 31 | 491,8 | 486,6 | -16,2729 | -19,7746 | 321,7893 | 264,8067 | 391,0339 |
| 32 | 495,2 | 491,8 | -12,8729 | -14,5746 | 187,6168 | 165,7111 | 212,4183 |
| 33 | 491,8 | 495,2 | -16,2729 | -11,1746 | 181,8426 | 264,8067 | 124,8712 |
| 34 | 496,1 | 491,8 | -11,9729 | -14,5746 | 174,4997 | 143,3499 | 212,4183 |
| 35 | 498,8 | 496,1 | -9,2729 | -10,2746 | 95,2749 | 85,9863 | 105,5669 |
| 36 | 501,5 | 498,8 | -6,5729 | -7,5746 | 49,7868 | 43,2028 | 57,3742 |
| 37 | 541 | 501,5 | 32,9271 | -4,8746 | -160,5058 | 1084,1951 | 23,7615 |
| 38 | 512,3 | 541 | 4,2271 | 34,6254 | 146,3658 | 17,8685 | 1198,9200 |
| 39 | 512,6 | 512,3 | 4,5271 | 5,9254 | 26,8251 | 20,4948 | 35,1106 |
| 40 | 511,5 | 512,6 | 3,4271 | 6,2254 | 21,3353 | 11,7451 | 38,7559 |
| 41 | 511,9 | 511,5 | 3,8271 | 5,1254 | 19,6156 | 14,6468 | 26,2700 |
| 42 | 513,9 | 511,9 | 5,8271 | 5,5254 | 32,1973 | 33,9553 | 30,5303 |
| 43 | 520 | 513,9 | 11,9271 | 7,5254 | 89,7566 | 142,2562 | 56,6320 |
| 44 | 515,9 | 520 | 7,8271 | 13,6254 | 106,6478 | 61,2638 | 185,6522 |
| 45 | 524,2 | 515,9 | 16,1271 | 9,5254 | 153,6176 | 260,0840 | 90,7337 |
| 46 | 527,1 | 524,2 | 19,0271 | 17,8254 | 339,1665 | 362,0312 | 317,7457 |
| 47 | 529,8 | 527,1 | 21,7271 | 20,7254 | 450,3037 | 472,0677 | 429,5432 |
| 48 | 534,9 | 529,8 | 26,8271 | 23,4254 | 628,4366 | 719,6943 | 548,7505 |
| 49 | 578,2 | 534,9 | 70,1271 | 28,5254 | 2000,4058 | 4917,8128 | 813,6998 |
| 50 | 539,4 | 578,2 | 31,3271 | 71,8254 | 2250,0836 | 981,3884 | 5158,8915 |
| 51 | 545,3 | 539,4 | 37,2271 | 33,0254 | 1229,4414 | 1385,8584 | 1090,6786 |
| 52 | 551,9 | 545,3 | 43,8271 | 38,9254 | 1705,9892 | 1920,8163 | 1515,1886 |
| 53 | 549,7 | 551,9 | 41,6271 | 45,5254 | 1895,0922 | 1732,8170 | 2072,5642 |
| 54 | 550,1 | 549,7 | 42,0271 | 43,3254 | 1820,8427 | 1766,2787 | 1877,0923 |
| 55 | 554 | 550,1 | 45,9271 | 43,7254 | 2008,1827 | 2109,3002 | 1911,9127 |
| 56 | 550 | 554 | 41,9271 | 47,6254 | 1996,7968 | 1757,8833 | 2268,1810 |
| 57 | 565,6 | 550 | 57,5271 | 43,6254 | 2509,6449 | 3309,3694 | 1903,1776 |
| 58 | 564,7 | 565,6 | 56,6271 | 59,2254 | 3353,7651 | 3206,6306 | 3507,6508 |
| 59 | 566,9 | 564,7 | 58,8271 | 58,3254 | 3431,1166 | 3460,6299 | 3401,8551 |
| 60 | 572,7 | 566,9 | 64,6271 | 60,5254 | 3911,5837 | 4176,6645 | 3663,3269 |
| Итого | 29973,6 | 29876,1 | 46980,9093 | 52640,2766 | 49558,8719 |
Рассчитав коэффициент автокорреляции второго порядка r2, получим количественную характеристику корреляционной связи рядов ![]() ,
, ![]() :
: ![]() .
.
Аналогично рассчитаем коэффициент автокорреляции третьего порядка: ![]() .
.
Можно сделать вывод, что наиболее целесообразно построение уравнения авторегрессии так как значение ![]() свидетельствует о наличии очень тесной связи между уровнями ряда с лагом в 1 месяц.
свидетельствует о наличии очень тесной связи между уровнями ряда с лагом в 1 месяц.
Похожие работы
... в построении модели, можно исправить в последующих циклах. В методологии моделирования, таким образом, заложены большие возможности саморазвития. Таким образом, мы рассмотрели сущность моделирования. Метод экономического моделирования, это одна из подгрупп метода прогнозирования. Особенность его применения в прогнозировании заключается в следующем: основа метода – сетевой график, имеющий много ...
... настоящее время можно сказать, что человечество обладает глубоким пониманием методологии применения математики в естественных науках. И хотя в экономике имеются определенные аналогии с физическими процессами, экономическое моделирование намного сложнее. Это объясняется в первую очередь тем, что экономика охватывает не только производственные процессы, но и производственные отношения. Моделирование ...
... же социально-экономической системе. Множественные равновесия являются естественным явлением в равновесных экономических моделях и моделях экономических игр. Тем не менее ввиду автономности моделей коррупции как направления социально-экономического моделирования, изучение таких наблюдаемых на практике явлений требует специального объяснения. Актуальность этого направления определяется тем, что в ...
... рынке труда и от традиций страны, его менталитета. Только в этом случае можно улучшить ситуацию в сфере занятости. Глава II. Формирование социально-экономической модели занятости в условиях переходной экономики Республики Казахстан Слабо регулируемое вхождение национальной экономики в рынок деформирует ход всех социально-эконоических процессов в республике, и ...
0 комментариев