Особенность схемотехники звеньев R-фильтров нижних частот

3. Особенность схемотехники звеньев R-фильтров нижних частот

Для звеньев второго порядка ФНЧ условие (4) можно исключить, тогда, как следует из (3), основные параметры будут иметь следующий вид

 (24)

Перебор вариантов реализации  показывает, что , поэтому параметры передаточной функции (5) можно конкретизировать:

 ,

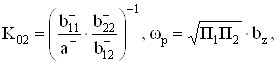
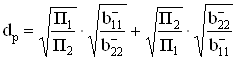. (25)

Таким образом, сдвиг частоты полюса в область более низких частот  сопровождается увеличением коэффициента усиления звена K₀₂. Однако в любом случае минимальное значение затухания полюса соответствует аналогичному параметру разделенной пассивной RC-цепи , что препятствует реализации ФНЧ со специальными свойствами (например, ФНЧ с линейной ФЧХ). Тогда при П₁=П₂,  в диапазоне рабочих частот

 (26)

. (27)

Таким образом, эффекта «перенапряжения» не наблюдается и верхняя граница динамического диапазона определяется соотношением (19), а собственный шум схемы – коэффициентом влияния (15)

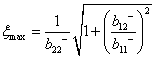(28)

и, следовательно, при большем К₀₂ первым ОУ. Однако при небольших коэффициентах передачи «вклад» ОУ в собственный шум схемы практически одинаков.

Полученные соотношения показывают, что основной задачей этапа схемотехнического проектирования безъемкостных ФНЧ является создание структур, в рамках которых параметрическая оптимизация обеспечивает реализацию любых значений добротности при более низком влиянии ОУ на собственный шум звена второго порядка. Как было показано ранее, решение такой задачи возможно применением принципа собственной компенсации влияния, по крайней мере, одного из ОУ. Для уменьшения затухания полюса, вызванного влиянием площади усиления доминирующего ОУ, на его выходе должна быть реализована передаточная функция ФНЧ, а возвратное отношение дополнительной (компенсирующей) обратной связи должно быть положительно.

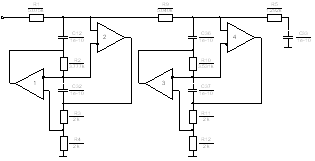
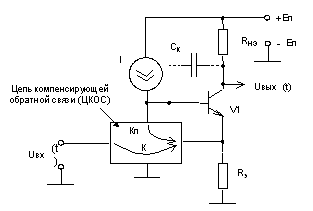
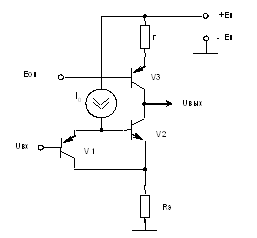
Принципиальная схема приведена на рис. 1.

Рис. 1. Звено R-фильтра с собственной компенсацией влияния ОУ2

Для наглядности и упрощения последующих соотношений будем использовать базовые параметры масштабных усилителей

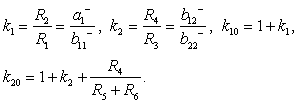 (29)

В базисе указанных аргументов параметры передаточной функции Ф2(р) будут определять следующими соотношениями

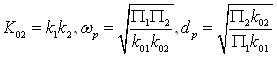 (30)

при выполнении параметрического условия собственной компенсации

 , при ,

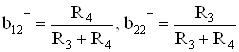, (31)

, где , .

Аналогично при тех же условиях определяются локальные передаточные функции

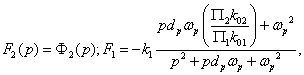(32)

(33)

Таким образом, как это следует из (19) и (20), максимальное выходное напряжение звена определится следующим выражением

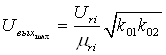 (34)

при условии

. (35)

Соотношение (35) является оценочным при .

При аналогичном допущении определяется коэффициент влияния ОУ1 и ОУ2 на собственный шум схемы

. (36)

Таким образом, введение компенсирующего контура обратной связи существенно уменьшило влияние ОУ2 на основные качественные показатели схемы звена второго порядка. Для построения и моделирования принципиальных схем разработан, ориентированный на SiGe технологию, SGB25VD (IHP) ОУ, базовые параметры которого показаны в табл. 2. Здесь и далее приводятся результаты моделирования принципиальных схем в среде Cadence.

Таблица 2

Основные параметры ОУ для технологии SGB25VD

, (дБ)	, (Ггц)	, (В/мкс)	, (В/мкс)	, (мВ)	, (Ом)	, (В)	, (мА)
38	2	900	425	400	50	1,5	5,5

Предварительно отметим, что возможность работать этого ОУ на низкоомную нагрузку и, следовательно, стандартную СВЧ линию позволяет совместить функцию фильтра и драйверного усилителя с заданным коэффициентом передачи. На рис. 2 приведены АЧХ и ФЧХ такого R-фильтра с коэффициентом передачи =30 дБ и добротностью  (кривые 1 и 2 соответственно). Здесь же для демонстрации эффективности действия контура компенсирующей обратной связи приведены аналогичные характеристики при , когда  (кривые 3 и 4).

Совпадение частоты полюса звена при различных добротностях показывает также недоминирующее влияние вторых полюсов используемых ОУ на параметры ФНЧ. Эффективность использования частотных свойств ОУ видна также из сопоставления АЧХ R-фильтра и АЧХ масштабных усилителей (кривая 5). Анализ временных характеристик ФНЧ (Q=1) при гармоническом входном воздействии различных уровней (рис. 3) показывает, что длительность переходного процесса согласуется с линейной моделью фильтра, а максимальное выходное напряжение (вторая гармоника соответствует максимальному коэффициенту передачи фильтра) не менее 100 мВ.

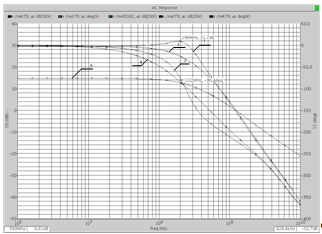
Рис. 2. Частотные характеристики R-ФНЧ

при разных добротностях полюса и k₀₂=30 дБ

 

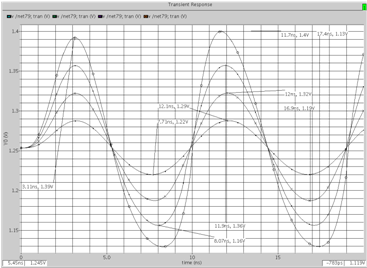
Рис. 3. К определению максимального выходного напряжения

R-ФНЧ с Q=1

Как видно из соотношений (25), увеличение частоты полюса ФНЧ связано с уменьшением его коэффициента передачи в полосе пропускания. Результаты моделирования и сопоставительного исследования схемы (рис. 1) на базе экспериментального ОУ (табл. 1) приведены в табл. 3.

Таблица 3

Результаты моделирования звена R-фильтра

с собственной компенсацией

, (дБ)	, (%)	, (МГц)	, (%)		, (%)	, (мВ)	, (дБ/дек)
30	1,5	222	25	1,22	7,4	100	36
0	0	642	29,4	1,19	5	100	36
Примечание. приращение коэффициента передачи фильтра в полосе пропускания, определяемое добротностью (затуханием) полюса.

Более детальное изучение приведенной в табл. 3 погрешности реакции основных параметров ФНЧ позволяет предположить, что указанное отклонение частоты полюса (), коэффициентов передачи () и () обусловлено эффектом умножения паразитной входной емкости дифференциальных каскадов ОУ, а также влиянием второго полюса его ФНЧ.

Однако область применения полученного устройства ограничивается уровнем его динамического диапазона, когда, как видно из (32) и (27), необходимость увеличения k₀₂, k₂ приводит к практически пропорциональному увеличению как масштабного коэффициента k_02min, так и . Кроме этого, для реализации  необходимость увеличения k₀₂(k₂) при ограниченном пределе  (27), как видно из (34), значительно увеличивает собственный шум всего устройства.

Снятие указанных структурных противоречий требует применения дополнительной общей отрицательной обратной связи и, следовательно, мультидифференциальных ОУ.