Взаимная компенсация емкостей подложки и нагрузки

4. Взаимная компенсация емкостей подложки и нагрузки

Применение предложенного выше принципа расширения диапазона рабочих частот может оказаться недостаточным для достижения конкретных целей проекта. Влияние емкости между выходной цепью транзистора и подложкой кристалла (Спi) действует эквивалентно емкости нагрузки и, следовательно, может оказаться доминирующим фактором. В этом случае

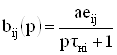, (26)

где  – коэффициент передачи цепи межкаскадной связи между i-м и j-м каскадами;  – эквивалентная постоянная времени цепи нагрузки i-го каскада; Сi – дополнительная емкость нагрузки i-го каскада.

Тогда, согласно (10) и табл. 1, при i=0  передаточная функция устройства будет иметь следующий вид:

. (27)

Учитывая, что

, (28)

получим

. (29)

Применив метод пополнения матрицы, когда

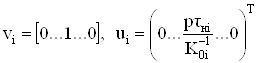, (30)

получим ряд

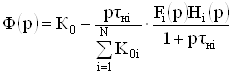, (31)

Где

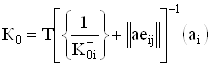 (32)

является коэффициентом передачи идеализированного усилителя (отсутствуют реактивные составляющие в моделях транзисторов),

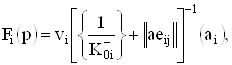 (33)

коэффициент передачи на выходе i-го каскада при выполнении аналогичных условий,

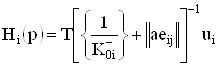(34)

передаточная функция на выходе схемы при подаче сигнала на конденсатор  (), входящий в структуру нагрузки i-го каскада.

Векторный сигнальный граф схемы, отображающий эти соотношения, приведен на рис. 8.

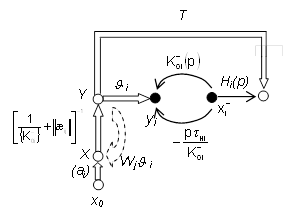
Рис. 8. Векторный сигнальный граф системы при влиянии Спi и Сi

Как отмечалось выше, условия собственной компенсации, вытекающие из (19), являются достаточными и единственными, поэтому сравнения соотношений (11) и (31), (12)–(14) и (32)–(33) показывают невозможность такой компенсации для емкостей нагрузки и подложки. Физическая сторона такого утверждения связана с электрической недоступностью заземленного узла Спi и Сi.

Действительно, как это видно из схемы (рис. 4), собственная компенсация осуществляется действием контура дополнительной (регенеративной) обратной связи через этот же проходной конденсатор. Отметим, что для указанного принципа компенсации такой вывод справедлив и при более сложной структуре паразитных постоянных времени активных элементов [6].

Невозможность собственной компенсации  требует детального исследования взаимной компенсации [6]. Для решения этой задачи введем матрицу , показанную на рис. 8 пунктиром. Невозможность собственной компенсации  требует детального исследования взаимной компенсации [6]. Для решения этой задачи введем матрицу , показанную на рис. 8 пунктиром.

Тогда

 (35)

Из системы (35) следует, что результирующее приращение коэффициента передачи К0 определяется следующим соотношением:

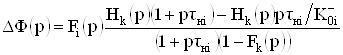, (36)

где

, (37)

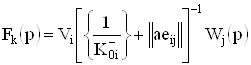. (38)

Следовательно, для компенсации влияния  необходимо выполнить условие

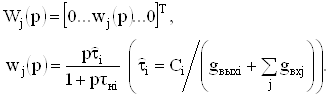 (39)

Действительно, в этом случае реализуется параметрическое равенство

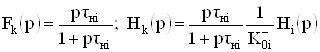, (40)

минимизирующее приращение (36).

Таким образом, для реализации принципа взаимной компенсации влияния эквивалентной емкости нагрузки i-го каскада необходимо выход j-го каскада усилителя подключить к выводу дополнительного (в данном случае компенсирующего) конденсатора Сi так, чтобы выполнить условия (40).

Если в структуре усилителя используется последовательное включение каскадов

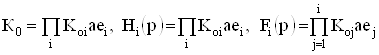, (41)

то это условие можно конкретизировать до численного значения дополнительного конденсатора

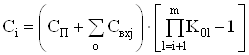. (42)

Настоящее соотношение показывает, что эффективность такого способа решения общей задачи зависит от идентичности процессов в тех компонентах, модели которых и характеризуют эти емкости. В этой связи в качестве Сi целесообразно использовать один из активных компонентов в соответствующем режиме работы.

Рассмотрим применение найденного принципа на примере трехкаскадного усилителя (рис. 9).

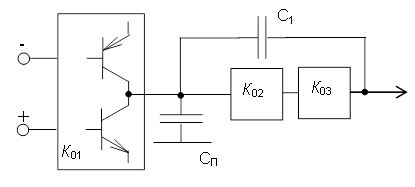
Рис. 9. Взаимная компенсация влияния Сп и С1 на частотные характеристики усилителя

Здесь при условии К0 ≈ К01 проводимости gвх2 и gвых1 достаточно малы, и влияние СП максимально, что и определяет ее доминирующее значение. В соответствии с (39)–(41) введение С1 при выполнении согласно соотношению (42) следующего условия

(43)

влияние С1 и СП исключается.

Недостатком взаимной компенсации является относительно высокая чувствительность этого условия к нестабильности Спi и Сi. Так, для указанного на рис. 9 случая относительная чувствительность постоянной времени усилителя и, следовательно, его граничной частоты

, (44)

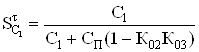 (45)

непосредственно определяется желаемым (достижимым) уровнем компенсации. Именно поэтому и будет наблюдаться режимная зависимость частоты единичного усиления такого устройства.

В этой связи кардинальным способом решения практических задач является переход на схемотехнику устройств с собственной компенсацией путем изменения геометрии транзисторов и создания под сформулированный здесь принцип «сигнальной» доступности подложки.

В этом случае компенсация влияния соответствующей паразитной емкости совпадает со структурой организации компенсирующего контура влияния .

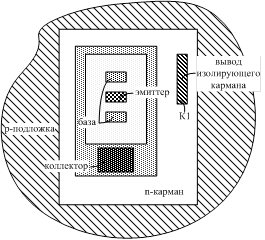
На рис. 10 показана топология p-n-p транзистора ФГУП НПП «Пульсар».

 

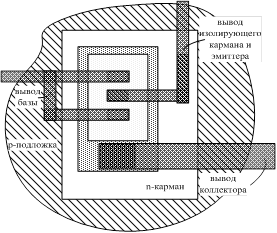
 а) б)

Рис. 10. Топология p-n-p транзистора ФГУП НПП «Пульсар» без компенсации Сп (а) и с компенсацией Сп (б)

Особенность изоляции p-n переходом такого транзистора состоит в том, что вывод от его изолирующего кармана К1 обычно подключается к шине положительного источника питания Еп при металлизации. Однако, если вывод К1 в конкретной схеме соединить с эмиттером p-n-p транзистора (рис. 10б), а эмиттер подключить к Еп через резистор Rэ, сопротивление которого в 510 раз превышает сопротивление эмиттерного перехода, то в соответствии с (42) эффективное значение емкости на подложку Сп уменьшается:

, (46)

где  – комплексный коэффициент передачи тока эмиттера;  – верхняя граничная частота коэффициента усиления по току эмиттера.

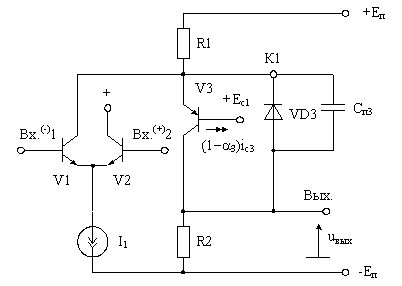
а)

б)

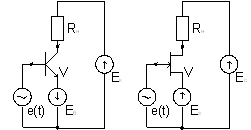
Рис. 11. Примеры собственной компенсации емкости на подложку p-n-p транзистора V3

Например, в схеме каскодного усилителя рис. 11а, сформированный таким образом вывод К1 от изолирующего кармана и эмиттера p-n-p транзистора V3 должен (для получения эффекта компенсации Сп3) соединяться с шиной положительного источника питания  через резистор . Это несколько сужает области практического использования такого технического решения, так как высокоомный резистор R1 не всегда удается реализовать. Поэтому в ряде случаев целесообразно введение дополнительного компенсирующего канала на транзисторе V2 (рис. 11б), что позволяет снять ограничение на способ соединения эмиттера входного транзистора V1 с шиной питания .

Так, для схемы рис. 11б в диапазоне частот  эффективная емкость на подложку выходного транзистора V3 согласно (42) определится следующим соотношением:

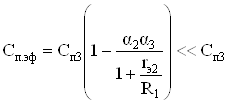,  (47)

компенсация дифференциальный каскад кристалл

где  – коэффициент передачи тока эмиттера транзисторов V2, V3.

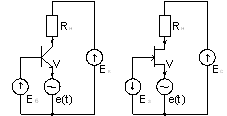
На рис. 12 показан вариант построения компенсирующего канала на транзисторе V2.

Рис. 12. Вариант построения компенсирующего канала на транзисторе V2

а)

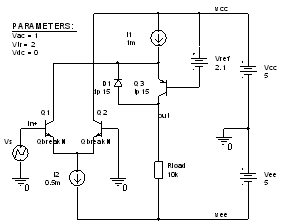
б)

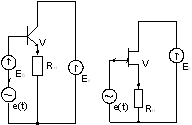
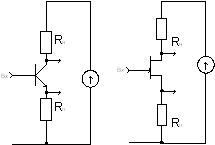
Рис. 13. Каскадный усилитель без компенсации Сп (а) и с компенсацией Сп (б)

На рис. 13 приведены схемы исследованных в среде PSpice каскодных усилителей со стандартной (рис. 13а) и предлагаемой (рис. 13б) топологией.

Рис. 1 ЛАЧХ коэффициента передачи по напряжению каскадных усилителей

Амплитудно-частотные характеристики усилителей рис. 13, представленные на рис. 14, свидетельствуют, что рассмотренный способ уменьшения влияния емкости на подложку расширяет частотный диапазон каскада в 6