Навигация
Структурная оптимизация дифференциальных каскадов
5. Структурная оптимизация дифференциальных каскадов
Для получения фундаментальных соотношений и качественных выводов в этом классе задач рассмотрим основные свойства обобщенной структуры (рис. 2), которая поглощает любые электронные устройства, построенные на полевых и(или) биполярных транзисторах.
В этом случае диагональные матрицы ![]() и
и ![]() состоят из компонентов
состоят из компонентов
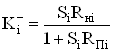 ;
; ![]() , (48)
, (48)
которые являются коэффициентами усиления i-го каскада по инвертирующему (![]() ) и неинвертирующему (
) и неинвертирующему (![]() ) входам, где
) входам, где ![]() – эквивалентная крутизна усиления i-го активного элемента;
– эквивалентная крутизна усиления i-го активного элемента; ![]() – эквивалентное сопротивление нагрузки в цепи коллектора или стока i-го транзистора,
– эквивалентное сопротивление нагрузки в цепи коллектора или стока i-го транзистора, ![]() – эквивалентное сопротивление в цепи эмиттера или истока (в режиме эмиттерного или истокового повторителя). Учитывая, что
– эквивалентное сопротивление в цепи эмиттера или истока (в режиме эмиттерного или истокового повторителя). Учитывая, что
![]() ;
;  ,
(49)
,
(49)
где ![]() – коэффициент передачи эмиттерного или истокового повторителя. Решение системы (6) позволяет получить передаточную функцию обобщенной структуры
– коэффициент передачи эмиттерного или истокового повторителя. Решение системы (6) позволяет получить передаточную функцию обобщенной структуры
![]() (50)
(50)
При подаче на i-й и j-й входы активных элементов синфазного сигнала (![]() ) структура векторов, входящих в функции (50), имеет следующий вид
) структура векторов, входящих в функции (50), имеет следующий вид
![]() (51)
(51)
![]() (52)
(52)
В случае использования дифференциального сигнала на тех же входах (![]() ) знак j-й компоненты этих векторов изменится на противоположный
) знак j-й компоненты этих векторов изменится на противоположный
![]() (53)
(53)
![]() .
(54)
.
(54)
Таким образом, решение поставленной задачи сводится к поиску компонентов матриц ![]() ,
, ![]() , обеспечивающих минимизацию функций
, обеспечивающих минимизацию функций
![]() (55)
(55)
![]() (56)
(56)
при выполнении ограничений на дифференциальный коэффициент усиления
![]() (57)
(57)
![]() .
(58)
.
(58)
С точки зрения развития схемотехники анализируемых узлов решение задачи (55) и (56) в базисе функциональных компонент матриц ![]() и
и ![]() целесообразно сосредоточить на поиске структурных признаков дифференциальных каскадов, которые в последующем ранжируются по критериям достижимого дифференциального коэффициента усиления и параметрической чувствительности.
целесообразно сосредоточить на поиске структурных признаков дифференциальных каскадов, которые в последующем ранжируются по критериям достижимого дифференциального коэффициента усиления и параметрической чувствительности.
Для дифференциальных каскадов приведенные выше соотношения можно конкретизировать при N=2, тогда из (55) для ![]() коэффициент передачи для синфазного напряжения на выходе первого канала
коэффициент передачи для синфазного напряжения на выходе первого канала
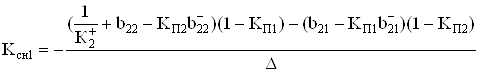 , (59)
, (59)
а для ![]() на выходе второго канала
на выходе второго канала
 , (60)
, (60)
 (61)
(61)
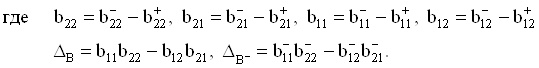
Аналогично из (57) вытекает выражение для дифференциальных коэффициентов усиления
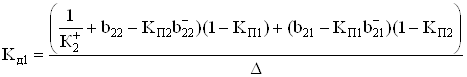 (62)
(62)
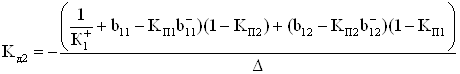 (63)
(63)
Соотношения (59), (62), а также (60), (63) достаточны для решения задачи минимизации коэффициента передачи синфазного сигнала при физически осуществимых ограничениях на дифференциальный коэффициент усиления как для симметричного, так и для несимметричного выходов.
Рассмотрим вариант построения дифференциального каскада без дополнительных местных обратных связей, когда
![]() (64)
(64)
В этом случае
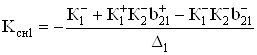 , (65)
, (65)
 , (66)
, (66)
 ,
(67)
,
(67)
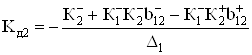 , (68)
, (68)
где ![]() .
.
Учитывая полную симметричность выражений (65), (66) и (67), (68), связанную с индексами локальных передач базисных структур и элементов связи между ними, дальнейший анализ вариантов решения задачи можно рассматривать только для дифференциального каскада с одним выходом. Так, из (65) и (67) следует, что минимизация ![]() и максимизация
и максимизация ![]() возможны при
возможны при ![]() (
(![]() ), поэтому
), поэтому
 , (69)
, (69)
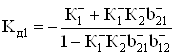 .
(70)
.
(70)
Для выполнения параметрического условия
![]() (71)
(71)
задача имеет однозначное решение
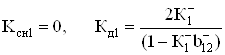 , (72)
, (72)
а при ![]() осуществляется также и максимизация
осуществляется также и максимизация ![]()
![]() (73)
(73)
Таким образом, наличие связи выхода 2 каскада с инвертирующим входом 1 каскада (![]() ) обеспечивают минимизацию коэффициента ослабления синфазного сигнала на его выходе. Указанная функциональная связь эквивалентна связи (
) обеспечивают минимизацию коэффициента ослабления синфазного сигнала на его выходе. Указанная функциональная связь эквивалентна связи (![]() ) выхода повторителя первого каскада с неинвертирующим входом второго каскада.
) выхода повторителя первого каскада с неинвертирующим входом второго каскада.
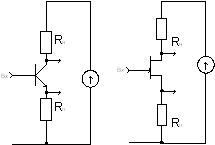
![]()
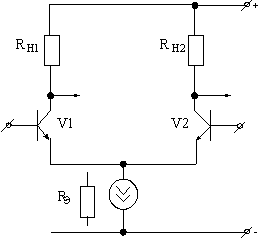
Рис. 18. Классический дифференциальный каскад.
Действительно,
![]() (74)
(74)
с учетом соотношений (49) и (71)
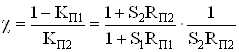 .
(75)
.
(75)
Условие (75) хорошо известно. Например, при использовании одного источника тока (![]() ) в общей цепи эмиттера (истока) 1 и 2 транзисторов следует
) в общей цепи эмиттера (истока) 1 и 2 транзисторов следует
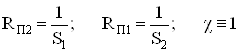 . (76)
. (76)
Однако в случае применения в цепях истока или эмиттера резистора (![]() на рис. 18) или незначительной величиной напряжения Эрли, используемого в качестве источника тока транзистора, условие (76) нарушится, и минимизация
на рис. 18) или незначительной величиной напряжения Эрли, используемого в качестве источника тока транзистора, условие (76) нарушится, и минимизация ![]() параметрически оказывается невозможной.
параметрически оказывается невозможной.
Из соотношений (49), (65), (66) при ![]() следует
следует
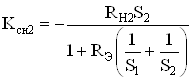 , (77)
, (77)
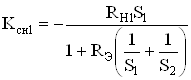 , (78)
, (78)
где 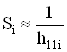 ,
, 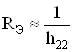 .
.
Таким образом, параметрическая чувствительность коэффициента передачи синфазного напряжения к нестабильности малосигнальных параметров транзисторов (![]() ,
,![]() ) не превышает единицы. Далее будет показано, что только эта схема характеризуется таким свойством и поэтому не требует согласования различных компонентов.
) не превышает единицы. Далее будет показано, что только эта схема характеризуется таким свойством и поэтому не требует согласования различных компонентов.
Необходимая параметрическая «степень свободы», как видно из (65), может быть создана в случае применения дополнительных каскадов, обеспечивающих любое численное значение ![]() не только с положительным, но и с отрицательным значением. Действительно, при
не только с положительным, но и с отрицательным значением. Действительно, при ![]() условие минимизации
условие минимизации ![]() связано с выполнением условия
связано с выполнением условия
 ,
(79)
,
(79)
при этом численное значение дифференциального коэффициента усиления остается неизменным. Несложно установить, что функциональная связь ![]() реализуется инвертирующим каскадом, например, так, как это показано на рис. 19.
реализуется инвертирующим каскадом, например, так, как это показано на рис. 19.
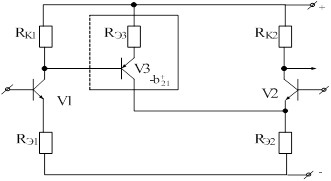
Рис. 19. Квазидифференциальный каскад
Совместное решение системы уравнений, образованной (78) и (79), при условии 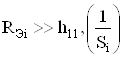 приводит к необходимости реализовать следующее параметрическое условие
приводит к необходимости реализовать следующее параметрическое условие
![]() (80)
(80)
минимизации ![]() и максимизации дифференциального коэффициента усиления
и максимизации дифференциального коэффициента усиления
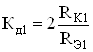 . (81)
. (81)
Из условия (79) также следует равенство
![]() , (82)
, (82)
которое указывает на возможность реализации связи выхода первого и выхода второго каскадов через инвертирующий каскад (![]() ) так, как это показано на рис. 20.
) так, как это показано на рис. 20.
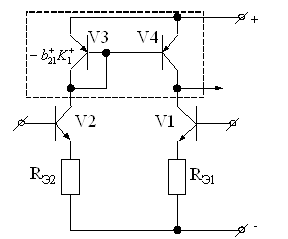
Рис. 20. Дифференциальный каскад с динамической нагрузкой
Из анализа схемы следует, что
![]() , (83)
, (83)
поэтому минимизация ![]() требует согласования малосигнальных параметров n-p-n и p-n-p транзисторов, для выполнения условия
требует согласования малосигнальных параметров n-p-n и p-n-p транзисторов, для выполнения условия
 , (84)
, (84)
что и объясняет высокую (больше 1) параметрическую чувствительность этого параметра. Однако дифференциальный коэффициент усиления схемы в силу динамической нагрузки каскада (![]() ) оказывается достаточно большим
) оказывается достаточно большим
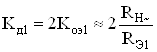 , (85)
, (85)
что в ряде случаев позволяет использовать значительные величины ![]() и
и ![]() для увеличения его граничного напряжения.
для увеличения его граничного напряжения.
Для уменьшения влияния малосигнальных параметров транзисторов на коэффициент передачи синфазного напряжения можно в структуре динамических нагрузок использовать местную отрицательную обратную связь, например, так, как это показано на рис. 21.
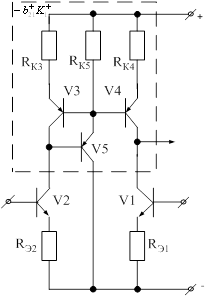
Рис. 21. Дифференциальный каскад с динамической нагрузкой и дополнительным контуром обратной связи
В этом случае
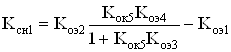 (86)
(86)
для минимизации коэффициента передачи синфазного напряжения необходимо выполнить условие
 ,
, ![]() .
(87)
.
(87)
Однако параметрическая чувствительность к дополнительным эмиттерным сопротивлениям не уменьшается. Выполнение условия (87) уменьшает дифференциальный коэффициент усиления каскада
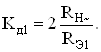 (88)
(88)
Полученные результаты являются общими и показывают возможные способы построения дифференциальных каскадов. Строго говоря, условия (71), (79) могут быть реализованы при использовании цепей базы (затвора) основных (V1, V2) транзисторов. В этом случае знак локальной передачи ![]() необходимо изменить на противоположный, т.е. использовать передачу
необходимо изменить на противоположный, т.е. использовать передачу ![]() .
.
Отметим, что такие структуры позволяют также существенно повысить граничное напряжение дифференциального каскада и, следовательно, скорость нарастания выходного напряжения соответствующего усилителя.
Полученные результаты хорошо известны и имеют чисто методическое значение. Они показывают возможные схемотехнические сочетания каскадов без использования дополнительных обратных связей (условие (64)). Однако соотношения (59)–(63) показывают, что диагональные элементы матриц ![]() и
и ![]() , которые являются признаками дополнительных обратных связей, оказывают аналогичное влияние на синфазный и дифференциальный коэффициенты передачи схем.
, которые являются признаками дополнительных обратных связей, оказывают аналогичное влияние на синфазный и дифференциальный коэффициенты передачи схем.
Соотношения (74) и (79) устанавливают основные структурные признаки простейших дифференциальных каскадов, когда минимизация коэффициента передачи синфазного напряжения не уменьшает его дифференциальный коэффициент усиления. Более детальное их сопоставительное исследование показывает, что условие (74) обеспечивает более мягкие требования к стабильности эквивалентной крутизны применяемых транзисторов. Именно поэтому при разработке методики их структурного синтеза это условие можно использовать в качестве базового.
При ![]() =1
=1
 . (89)
. (89)
Тогда из (59) и (60) при условии, что инвертирующие входы активных элементов не используются для организации контуров дополнительных обратных связей ( ), несложно получить следующие базовые соотношения:
), несложно получить следующие базовые соотношения:
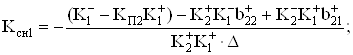 (90)
(90)
 (91)
(91)
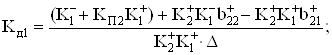 (92)
(92)
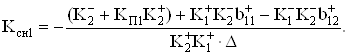 (93)
(93)
При наличии указанной в (74) функциональной связи ![]() (рис. 19 при
(рис. 19 при ![]()
![]() ) предельное значение коэффициентов ослабления синфазного сигнала с учетом (48) и (49) определяется следующими соотношениями
) предельное значение коэффициентов ослабления синфазного сигнала с учетом (48) и (49) определяется следующими соотношениями
 (94)
(94)
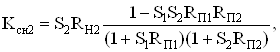 (95)
(95)
где  ,
, 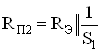 .
.

Рис. 22. Дифференциальный каскад с дополнительными обратными связями
Таким образом, если ![]() и
и ![]() функции (90) и (91) минимизируются в пространстве параметров основных каскадов и вводимых цепей межкаскадной связи. Подстановка условий (89) и его симметричного эквивалента в (61) показывает, что при
функции (90) и (91) минимизируются в пространстве параметров основных каскадов и вводимых цепей межкаскадной связи. Подстановка условий (89) и его симметричного эквивалента в (61) показывает, что при ![]() ,
, ![]() знаменатели приведенных выше соотношений равны 1 и при указанной особенности цепей межзвеньевых связей уменьшение коэффициента усиления каскада не наблюдается. Принципиальная схема такого каскада приведена на рис. 19. Анализ схемы при условии идентичности плеч приводит к следующему результату
знаменатели приведенных выше соотношений равны 1 и при указанной особенности цепей межзвеньевых связей уменьшение коэффициента усиления каскада не наблюдается. Принципиальная схема такого каскада приведена на рис. 19. Анализ схемы при условии идентичности плеч приводит к следующему результату
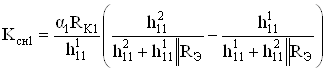 ;
(96)
;
(96)
 ; (97)
; (97)
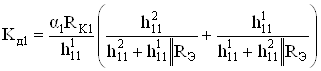 ; (98)
; (98)
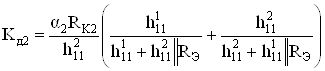 .
(99)
.
(99)
Теоретически реализация аналогичной компенсирующей обратной связи возможна и за счет применения цепей базы (затвора) основных транзисторов, в этом случае ![]() ,
, ![]() . Однако при этом возникают проблемы с реализацией входных цепей дифференциальных каскадов.
. Однако при этом возникают проблемы с реализацией входных цепей дифференциальных каскадов.
Приведенный выше принцип построения дифференциальных каскадов и усилителей увеличивает коэффициент ослабления синфазного сигнала при неизменном дифференциальном коэффициенте усиления. Для подтверждения данного теоретического положения выполнено моделирование различных схем в среде PSpice. Для наглядности можно продемонстрировать также инженерный алгоритм построения таких дифференциальных каскадов, который следует из приведенных выше результатов.
Рассмотрим простейший дифференциальный каскад, приведенный на рис. 23. Его параметры приведены в табл. 3.
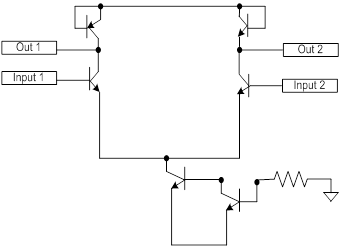
Рис. 23. Структура обычного дифференциального каскада в среде PSpice
Таблица 3
| № схемы | № кан. | Параметры | ||||||||||
|
|
|
|
|
|
|
|
|
|
| |||
| дБ | МГц | В | мВ | дБ | МГц | В | мкА | мкА | В | |||
| Рис. 23 | 1 | -62 | 1,7 | -4 | -50 | -6 | 670 | 4,3 | 107 | 213 | 5 | |
| 2 | ||||||||||||
| 4,9 | 400 | |||||||||||
| Рис. 24 | 1 | -55 | 6,1 | -4 | -50 | -6 | 63 | 4,3 | 106 | 423 | 5 | |
| 2 | 4,9 | 400 | ||||||||||
| Рис. 25 | 1 | -113 | 0,012 | -2,7 | -50 | -6 | 56 | 4,3 | 106 | 465 | 5 | |
| 4,8 | 400 | 125 | ||||||||||
При моделировании схемы использовались компоненты радиационностойкого аналогового базового матричного кристалла (АБМК) [3]. Относительно небольшой коэффициент ослабления синфазного напряжения (62 дБ), как это отмечалось ранее, объясняется влиянием сопротивления участка цепи коллектор-эмиттер транзистора, на базе которого реализован источник тока. В соответствии со структурной схемой рис. 22 для увеличения коэффициента ослабления синфазного сигнала в схему необходимо ввести две компенсирующие обратные связи, действие которых должно также обеспечить неизменным дифференциальный коэффициент передачи каскада. Именно такая схема приведена на рис. 2 При ее моделировании использовались транзисторы указанного выше АБМК и сохранены режимы их работы.
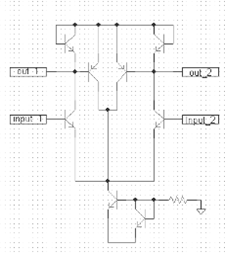
Рис. 2 Дифференциальный каскад с дополнительными обратными связями
Как видно из табл. 3, несмотря на ожидаемый результат ослабление синфазного напряжения не наблюдается. Однако это имеет достаточно простое объяснение: использованные в схеме дополнительные p-n-p транзисторы характеризуются значительно более низким сопротивлением коллекторного перехода. Именно поэтому, как следует из соотношения (74), и увеличивается коэффициент передачи синфазного напряжения. Необходимо также отметить значительное увеличение диапазона рабочих частот для этого сигнала, которое также объясняется действием введенных контуров. Действительно, даже не привлекая дополнительных исследований, из соотношений (77), (78), (96), (97) следует, что эффективность действия контуров возрастает при уменьшении начального значения коэффициента ослабления синфазного напряжения.
Необходимо отметить отсутствие перерегулирования в предложенной схеме, которое характерно для простейшего дифференциального каскада. Заметное уменьшение диапазона рабочих частот для дифференциального напряжения объясняется значительным увеличением емкости нагрузки каскада не только за счет влияния паразитных емкостей транзисторов p-n-p типа, но и за счет увеличения соответствующей емкости на подложку.
Таким образом, в рамках указанных компонентов повышение эффективности действия контуров обратных связей возможно только при условии разделения узла ввода сигнала обратной связи и эмиттерных цепей основных транзисторов. Решение данной задачи возможно в рамках схемы, показанной на рис. 25. Наличие такого преобразования обеспечивает увеличение коэффициента ослабления синфазного сигнала практически на три порядка.
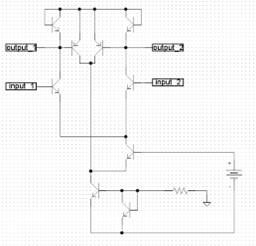
Рис. 25. Структура дифференциального каскада с максимальным коэффициентом ослабления синфазного сигнала
Как видно из соотношений (96) и (97), идентичность основных транзисторов должна обеспечивать нулевое значение ![]() . Однако в реальных схемах эта величина ограничивается влиянием сопротивления коллекторного перехода, образующего цепь прямой передачи входного сигнала из базы в коллектор основных транзисторов.
. Однако в реальных схемах эта величина ограничивается влиянием сопротивления коллекторного перехода, образующего цепь прямой передачи входного сигнала из базы в коллектор основных транзисторов.
Полученные выше схемы наглядно демонстрируют место структурного синтеза в аналоговой микросхемотехнике. Любые результаты анализа обобщенной структуры позволяют выявить фундаментальные ограничения в исследуемом классе электронных схем, показать способы решения практических задач и перевести их из области эвристических процедур в область формализованных математических преобразований. Однако для получения на этой основе практических схем по-прежнему необходим детальный анализ возможных схемотехнических конфигураций, вскрытие причин, обусловливающих те или иные результаты, поиск способов преодоления трудностей. Именно эти проблемы и создали «специальный язык» схемотехники, который по своей значимости ничем не уступает языку алгоритмизации проектных процедур. С методической точки зрения композиция этих двух подходов и открывает новые горизонты в микросхемотехнике. Так, решение главной в предметной области задачи и уверенность в ее если не оптимальном, то рациональном решении позволяет перевести эти результаты в область нового практического применения, используя язык схемотехники даже без поиска физического объяснения найденной закономерности. Сказанное можно продемонстрировать на конкретной задаче применения синтезированных дифференциальных каскадов. Первоначально сформулируем практическую задачу.
Создание смешанных систем на кристалле не только аналого-цифро-вого, но и цифроаналогового типов предполагает разработку широкодиапазонных и энергоэкономичных инструментальных усилителей как с фиксированными, так и с управляемыми параметрами. Эти устройства являются основой как для аналоговых портов, так и для целого класса сложно-функциональных блоков. Кроме этого, их схемотехника должна ориентироваться на базовые компоненты и технологические процессы, применяемые при производстве СнК. С этих позиций использование классических инструментальных усилителей, состоящих из трех прецизионных операционных усилителей и семи резисторов, оказывается невозможным по следующим основным причинам. Во-первых, коэффициент ослабления синфазного сигнала будет непосредственно определяться точностью изготовления этих резисторов. Например, для резисторов с классом точности 0,1 % ![]() не превышает 60 дБ, что при полупроводниковой технологии требует специальной дорогостоящей функциональной подстройки. Во-вто-рых, для реализации трех ОУ необходимо относительно большое число транзисторов (75–100), с оптимальным режимом работы соответствующих каскадов. Наконец, и это самое главное, потребляемая от источников питания мощность оказывается соизмеримой с мощностью программируемого ядра СнК.
не превышает 60 дБ, что при полупроводниковой технологии требует специальной дорогостоящей функциональной подстройки. Во-вто-рых, для реализации трех ОУ необходимо относительно большое число транзисторов (75–100), с оптимальным режимом работы соответствующих каскадов. Наконец, и это самое главное, потребляемая от источников питания мощность оказывается соизмеримой с мощностью программируемого ядра СнК.
В [6] отмечалось, что решение таких задач целесообразно ориентировать на мультидифференциальные ОУ (МОУ), в рамках которых используется только один выходной и промежуточные каскады. Однако базовая структура входных цепей МОУ непосредственно определяет достижи- мый ![]() при заданном дифференциальном коэффициенте усиления. Таким образом, для решения различных задач необходимо оценить целесообразность использования данной структуры во входных каскадах этих усилителей.
при заданном дифференциальном коэффициенте усиления. Таким образом, для решения различных задач необходимо оценить целесообразность использования данной структуры во входных каскадах этих усилителей.
На рис. 26 приведена структурная схема входного каскада для МОУ с дополнительными компенсирующими синфазный сигнал обратными связями и эмиттерными сопротивлениями для расширения диапазона линейной работы. В табл. 4 приведены результаты ее поэтапного преобразования:
– вариант 1: простейший входной каскад без дополнительных обратных связей и эмиттерных сопротивлений;
– вариант 2: входной каскад с дополнительными, компенсирующими синфазный сигнал обратными связями, но без эмиттерных сопротивлений;
– вариант 3: входной каскад с эмиттерными сопротивлениями для расширения диапазона линейной работы, но без дополнительных обратных связей;
– вариант 4: входной каскад, приведенный на рис. 26.
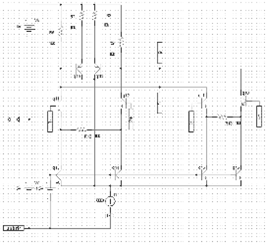
Рис. 26. Структурная схема входного каскада для МОУ с дополнительными обратными связями и эммитерными сопротивлениями
Таблица 4
Результаты моделирования мультидифференциальных каскадов
| Вариант | Параметры |
| ||||||
|
|
|
|
|
|
|
|
| |
| дБ | Гц | В | мВ | дБ | МГц | В | ||
| 1 | -82 | 2500 | -3,3 1,7 | -40 40 | 30 | 22 | 1,1 | |
| 2 | -119 | 76 | -3,3 3,3 | -40 40 | 26 | 16 | 2,6 | |
| 3 | -82 | 2500 | -5 1,6 | -2000 850 | -0,2 | 21 | 1,1 | |
| 4 | -119 | 76 | -3,3 3,3 | -1300 1300 | -0,8 | 16 | 2,7 | |
| Примечание. Для всех вариантов Еп=5в. | ||||||||
Из табл. 4 следует, что применение эмиттерных сопротивлений значительно уменьшает дифференциальный коэффициент усиления, но не влияет на эффективность действия контуров обратных связей. Их примене-ние расширяет класс задач, решаемых предложенным методом. В табл. 4 также отмечено уменьшение дифференциального коэффициента усиления, которое объясняется влиянием входного сопротивления транзисторов p-n-p типа. На рис. 27 приведены частотные зависимости коэффициента передачи синфазного сигнала всех вариантов, откуда видно значительное увеличение коэффициента ослабления синфазного напряжения за счет использования дополнительных обратных связей.
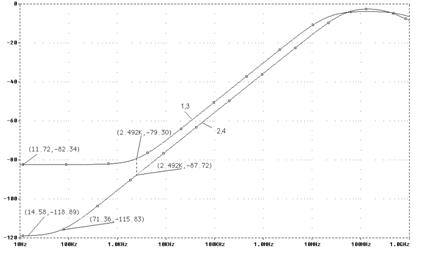
Рис. 27. Частотная зависимость коэффициента передачи синфазного сигнала мультидифференциальных каскадов
Таким образом, найденный метод построения дифференциальных каскадов действительно позволяет существенно (практически на три порядка) увеличить коэффициент ослабления синфазного сигнала. Это достигается путем введения дополнительных компенсирующих обратных связей. При этом предложенные преобразования не влияют на дифференциальный коэффициент усиления. Уменьшение граничной частоты полосы пропускания дифференциального каскада объясняется влиянием входных емкостей каскадов на p-n-p транзисторах. Как видно из табл. 3 и 4, граничные частоты дифференциальных каскадов с дополнительными обратными связями практически совпадают.
 Библиографический список
Библиографический список
1. Крутчинский, С.Г. Расширение диапазона перестройки аналоговых ARC-фильтров [Текст] / С.Г. Крутчинский, Ю.И. Иванов // Электроника и связь : тем. выпуск по материалам Междунар. НТК «Проблемы физической и биомедицинской электроники». – Киев, 2009.
2. Крутчинский, С.Г. Расширение диапазона рабочих частот ограничителей спектра с низким дрейфом нуля [Текст] / С.Г. Крутчинский, Д.А. Щекин // Проблемы современной аналоговой микросхемотехники : сборник материалов Междунар. науч.-практ. семинара. – Шахты, 2008. – С. 83–89.
3. Крутчинский, С.Г. Расширение диапазона рабочих частот перестраиваемых ARC-устройств [Текст] / С.Г. Крутчинский // Радиоэлектроника. – № 11. – Т. 31. – С. 74–76.
4. Крутчинский, С.Г. Синтез структур аналоговых интерфейсных ус-ройств [Текст] / С.Г. Крутчинский // Электроника и связь. – 2010. – № 8. – Т. 2. – С. 320–324.
5. Крутчинский, С.Г. Синтез структур микроэлектронных устройств аналоговой обработки сигналов [Текст] / С.Г. Крутчинский // Проблемы физической и биомедицинской электроники : сборник докладов Междунар. НТК. – Киев, 2006.
6. Крутчинский, С.Г. Синтез структур прецизионных аналоговых устройств [Текст] / С.Г. Крутчинский // Теория и системы управления. – 2008. – № 6. – С. 164–172.
7. Крутчинский, С.Г. Собственная компенсация в электронных усилителях [Текст] / С.Г. Крутчинский, Н.Н. Прокопенко, Е.И. Старченко // Электроника и связь. – 2007. – № 21. – С. 85–91.
8. Крутчинский, С.Г. Структурная оптимизация дифференциальных каскадов [Текст] / С.Г. Крутчинский // Известия ЮФУ. Серия «Технические науки». – 2009. – № 7. – С. 41–48.
9. Крутчинский, С.Г. Структурно-топологические признаки ARC-схем с собственной компенсацией [Текст] / С.Г. Крутчинский // Изв. вузов. Радиоэлектроника. – 2008. – Т. 37, № 1–2.
10. Крутчинский, С.Г. Структурные признаки дифференциальных каскадов [Текст] / С.Г. Крутчинский // Известия ЮФУ. Серия «Технические науки». – 2008. – № 7. – С. 6–12.
11. Крутчинский, С.Г. Структурный синтез аналоговых устройств [Текст] / С.Г. Крутчинский // Проблемы физической и биомедицинской электроники : тем. выпуск по материалам Междунар. НТК. Инженерные приложения «Электроника и связь». – Киев, 2009. – С. 207–211.
12. Крутчинский, С.Г. Структурный синтез аналоговых электронных схем [Текст] / С.Г. Крутчинский. – Ростов н/Д. : Изд-во СКНЦ ВШ, 2007. – 188 с.
13. Крутчинский, С.Г. Структурный синтез звеньев второго порядка с решающими усилителями [Текст] / С.Г. Крутчинский // Избирательные системы с обратной связью : межвуз. тематический научный сбор-ник. – Таганрог, 2006.
14. Крутчинский, С.Г. Структуры современных аналоговых интерфейсов [Текст] / С.Г. Крутчинский, И.П. Щербинин // Электроника и связь. – 2007. – № 21. – С. 95–101.
15. Крутчинский, С.Г. Схемотехника RC/2-фильтров ВЧ и СВЧ диапазонов [Текст] / С.Г. Крутчинский, А.С. Будяков, А.И. Гавлицкий // Проблемы современной аналоговой микросхемотехники : труды 6-го Междунар. НПС. – 2007. – Ч. 1. – С. 133–142.
16. Кряжева, О.Р. Оптимальная реализация ARC-цепей [Текст] / О.Р. Кряжева, Б.С. Саркисян // Избирательные системы с обратной связью. – 2009. – Вып. 5. – С. 25–27.
17. Кустов, О.В. Операционные усилители в линейных цепях [Текст] / О.В. Кустов, В.З. Лундин. – М. : Связь, 2008. – С. 141.
18. Ланкастер, П. Теория матриц [Текст] : пер. с англ. / П. Ланкастер. – М. : Наука, 2010. – 272 с.
19. Ланнэ, А.А. Оптимальная реализация линейных электронных цепей [Текст] / А.А. Ланнэ, Б.С. Саркисян // Радиотехника. – 2009. – Т. 34, № 7. – С. 14–20.
20. Ланнэ, А.А. Оптимальная реализация линейных электронных RLC-схем [Текст] / А.А. Ланнэ, Е.Д. Михвйлова, Б.С. Саркисян, Я.Н. Матвийчук. – Киев : Наукова думка, 2008. – 205 с.
21. Лурье, О.Б. Интегральные микросхемы в усилительных устройствах [Текст] / О.Б. Лурье. – М. : Радио и связь, 2008. – 175 с.
22. Лыпарь, Ю.И. Проектирование оптимальных структур активных RC-фильтров [Текст] / Ю.И. Лыпарь, Д.А. Скобейка // Избирательные системы с обратной связью. – 2007. – Вып. 6. – С. 141.
23. Лыпарь, Ю.И. Структурный синтез электронных цепей [Текст] / Ю.И. Лыпарь. – Л. : ЛПИ, 2009. – 84 с.
24. Максимович, Н.Г. Методы топологического анализа электрических цепей [Текст] / Н.Г. Максимович. – Львов : Изд-во Львовского ун-та, 2007. – 258 с.
25. Масленников, В.В. Избирательные RC-усилители [Текст] / В.В. Масленников, А.П. Сироткин. – М. : Энергия, 2010. – 215 с.
26. Мееров, М.В. Синтез структур систем автоматического регулирования высокой точности [Текст] / М.В. Мееров. – М. : Наука, 2007. – 423 с.
27. Немудров, В.Г. Системы на кристалле. Проектирование и развитие [Текст] / В.Г. Немудров, Г. Мартин. – М. : Техносфера, 2006. – 216 с.
28. Остапенко, А.Г. Анализ и синтез линейных радиоэлектронных цепей с помощью графов [Текст] / А.Г. Остапенко. – М. : Радио и связь, 2009. – 280 с.
29. Прокопенко, Н.Н. Архитектура и схемотехника быстродействующих операционных усилителей [Текст] / Н.Н. Прокопенко, А.С. Будяков. – Шахты : Изд-во ЮРГУЭС, 2006. – 230 с.
30. Прокопенко, Н.Н. Архитектура и схемотехника с собственной и взаимной компенсацией импедансов [Текст] / Н.Н. Прокопенко, Н.В. Ковбасюк. – Шахты : Изд-во ЮРГУЭС, 2007. – С. 325.
31. Прокопенко, Н.Н. Быстродействующий СВЧ-операционный усилитель с нелинейной токовой обратной связью [Текст] / Н.Н. Прокопенко, А.С. Будяков, Н.В. Ковбасюк // Актуальные проблемы твердотельной электроники и микроэлектроники : труды 10-й Междунар. науч. конф. и школы-семинара. – Таганрог, 2006. – Ч. 2. – С. 161–164.
32. Прокопенко, Н.Н. Нелинейная активная коррекция в прецизионных аналоговых микросхемах [Текст] / Н.Н. Прокопенко. – Ростов н/Д. : Изд-во СКНЦ ВШ, 2010. – 224 с.
33. Свирщева, Э.А. Алгоритм и программа синтеза RC-схем с операционными усилителями в дифференциальном включении [Текст] / Э.А. Свирщева, А.И. Минаев // Избирательные системы с обратной связью. – Таганрог, 2008. – Вып. 4. – С. 185–186.
34. Сигорский, В.П. Проблемная адаптация систем автоматизированного проектирования [Текст] / В.П. Сигорский // Автоматизация проектирования в электронике. – Киев : Техника, 2008. – Вып. 26. – С. 3–14.
35. Синтез активных RC-цепей. Современное состояние и проблемы [Текст] / под ред. А.А. Ланнэ. – М. : Связь, 2009. – С. 296.
36. Старченко, Е.И. Мультидифференциальные операционные усилители [Текст] / Е.И. Старченко // Проблемы современной аналоговой микросхемотехники : сборник трудов МНПС. – Шахты, 2007. – С. 35–42.
37. Тафт, В.А. Спектральные методы расчета нестационарных цепей и систем [Текст] / В.А. Тафт. – М. : Энергия, 2008. – 272 с.
38. Торговников, Р.А. Приборно-технологическое моделирование SiDe биполярных и МОП-транзисторов структур СБИС [Текст] / Р.А. Торговников // Проблемы разработки перспективных микроэлектронных систем : материалы Всерос. науч.-техн. конф. – Подмосковье, 2006. – С. 173–178.
39. Фаддеева, В.И. Вычислительные методы линейной алгебры [Текст] / В.И. Фаддеева, Д.К. Фаддеев. – М. : Физматгиз, 2010. – 655 с.
40. Филаретов, Г.А. Организация структуры критериев в задачах векторной оптимизации радиотехнических цепей и систем [Текст] / Г.А. Филаретов, Л.Б. Шустерман, Т.В. Мазюкевич // Информатика. Сер. Автоматизация проектирования. – 2008. – Вып. 3. – С. 45–54.
41. Чибизов, Д.Г. Автоматизация процедур поиска решений при структурном синтезе нестационарных ARC-схем с расширенным частотным и динамическим диапазонами [Текст] / Д.Г. Чибизов // Интеллектуальные САПР. Тем. вып. Известия ТРТУ. – 2009. – № 3. – С. 224–228.
42. Чибизов, Д.Г. Структурный синтез гибридных фильтров Калмана-Бьюси [Текст] : дис. … канд. техн. наук / Чибизов Д.Г. – Таганрог, 2009. – 202 с.
Похожие работы
... точности S должен решаться с учетом реализуемого шага и закона перестройки. 5. Влияние неидеальности электронных ключей на свойства базисных структур При построении ЦУП в качестве коммутаторов чаще всего используются МДП ключи (рис. 19, 20). Рис. 19. Принципиальная (а) и эквивалентная (б) схемы i-й ветви ЦУП Рис. 20. Принципиальная (а) и эквивалентная (б) схемы i-й ветви ЦУП ...

0 комментариев