Моделирование конструкций конечными элементами

1.1 Моделирование конструкций конечными элементами

Основой построения расчетной модели служит библиотека конечных элементов. Моделирование конечными элементами предполагает достижение трех целей:

моделирование геометрии деформируемого тела;

моделирование упруго-массовых свойств конструкции;

моделирование граничных условий.

Геометрия конструкции моделируется совокупностью элементов различной размерности и различных форм, представляющих три группы:

одномерные элементы, имеющие форму прямой линии или дуги окружности;

двумерные элементы треугольной и четырехугольной формы;

трехмерные элементы - тетраэдры, гексаэдры и пятигранники.

При моделировании требуемых упруго-массовых свойств конструкции кроме геометрии конечных элементов учитываются их свойства, то есть способность воспринимать нагрузку и испытывать деформацию определенного вида. Так, например, некоторая часть одномерных элементов конструкции может работать только на растяжение-сжатие, а другая может к тому же воспринимать изгиб и кручение.

Для моделирования граничных условий и массовых свойств конструкции предназначены специальные элементы, образующие группу «другие» (other).

Расположение элемента в пространстве зависит от координат узлов, принадлежащих элементу. В узлах определяются обобщенные узловые смещения. Узловыми смещениями могут быть компоненты вектора перемещений вдоль осей координат и углы поворота элемента в узлах вокруг осей координат. Обобщенные узловые смещения обозначаются термином степени свободы или сокращенно DOF (degrees of freedom).

Набор или список степеней свободы модели зависит от типа элементов, используемых при моделировании.

Так, в узлах элементов работающих на изгиб и кручение (элементы балки и оболочки) определены все шесть компонентов смещений, а в узлах трехмерных элементов - только перемещения вдоль осей координат. Если в модели нет элементов, работающих на изгиб, то список степеней свобод не будет содержать углы поворота элементов в узлах. Это не означает, что их нет, просто углы поворота не оказывают влияние на величину полной потенциальной энергии конструкции.

1.2 Нагрузочные режимы

В процессе эксплуатации на КМ действуют нагрузки, возникающие при ее движении по дорожной поверхности, которые обычно носят случайный характер. Их можно подразделить на случайные и детерминированные. Эти нагрузки действуют на несущую систему КМ и образуют пространственную систему. Определение величин и направлений нагрузок - достаточно сложная задача, поэтому при расчетах из всей совокупности учитывают нагрузки, которые возникают в экстремальных условиях эксплуатации (предельные нагрузки) (рис. 1.2.1).

Рассмотрим экстремальные детерминированные нагрузки и соответствующие им режимы эксплуатации. Статические расчеты несущих систем КМ выполняют для симметричных (изгиб), кососимметричных (кручение) и боковых (в горизонтальной плоскости) нагрузок.

Вертикальную симметричную нагрузку R_Z (рис. 1.2.1, а) можно вычислить, используя выражение

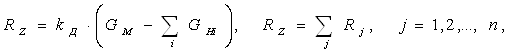
где G_Hj - вес i-го неподрессоренного узла или агрегата КМ, k_Д -коэффициент динамичности, принимаемый в зависимости от типа КМ: для грузовых

k_Д = 3,0; для КМ высокой проходимости k_Д = 3,5...4,0; для легковых КМ и автобусов k_Д =2,0...2,5; п - число колес, взаимодействующих с опорной поверхностью.

Вертикальная несимметричная нагрузка возникает при наезде колесом на препятствие и при вывешивании колеса (или колес) (рис. 1.2.1, б). В первом случае вертикальную несимметричную нагрузку можно определить по приведенной выше формуле, учитывая, что k_Д = 1,5 для грузовых КМ;

k_Д = 1,8 для автомобилей высокой проходимости; k_Д = 1,3 для легковых КМ и автобусов.

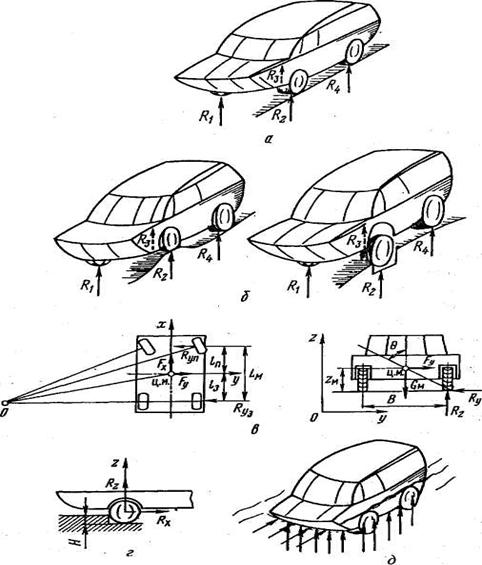
Рис. 1.2.1. Расчетные режимы нагружения: а - вертикальная симметричная нагрузка; б - наезд колесом на препятствие и вывешивание колеса; в - горизонтальная нагрузка при движении по криволинейной траектории; г - наезд колесом на ступенчатое препятствие; д - движение КМ по воде

Момент, закручивающий несущую систему, равен

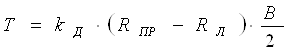
Здесь R_ПР, R_Л - нагрузки на правом (R₁) и левом (R₂) передних колесах соответственно, В - колея.

При расчете несущей системы на изгиб от действия вертикальных нагрузок необходимо учитывать координаты точек их приложения. Динамические нагрузки в этом случае характеризуются эмпирическими коэффициентами (например, коэффициентом динамичности).

Боковые силы действуют на КМ при ее движении по криволинейной траектории (рис. 1.2.1, в), в случае появления несимметричных нагрузок при тяговом и тормозном режимах, а также при боковом столкновении с препятствием.

Максимально возможная центробежная сила Fy до переворота при криволинейном движении определяется следующим выражением (см. рис. 1.2.1. в)

где R_y – реакция от дороги на колёса, z_M – расстояние от опорной поверхности до центра масс КМ. При этом

l_З, l_П – расстояние соответственно от задней и передней осей до центра масс. Для случая на рис. 1.2.1, г

R_Z0 - статическая нагрузка на переднюю ось; в = arctg[l — H/r_d], где r_d - динамический радиус колеса; Н - высота препятствия.

Наибольшие горизонтальные нагрузки возникают при повороте и боковом ударе о препятствие и могут составлять до 80 % от веса КМ, приходящегося на ось; в случае несимметричных нагрузок при тяговом и тормозном режимах - порядка 8 % от веса КМ.

При боковом ударе передним колесом о препятствие на КМ действуют нагрузки, наибольшая из которых изгибает несущую систему в горизонтальной плоскости. В случае экстремального режима боковая нагрузка пропорциональна весу КМ и коэффициенту k_σсцепления колеса с поверхностью дороги (с учетом коэффициента динамичности):

При наезде КМ передним колесом на препятствие на колесо действует сила, которую можно разложить на продольную R_x и вертикальную R_z(рис. 1.2.1, г). Вертикальная нагрузка может приводить к закручиванию несущей системы. Причем в этом случае крутящий момент, как правило, меньше, чем в режиме вывешивания колес. Поэтому при расчете несущей системы КМ воспользуемся силой R_x, приводящей к изгибу и сдвигу элементов несущей системы в горизонтальной плоскости

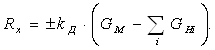
Для плавающих КМ следует учитывать выталкивающую силу воды и давления встречного потока (рис. 1.2.1, д).

Из рассмотренных выше режимов наихудшим по параметрам прочности и жесткости несущих систем является режим преодоления коротких препятствий (углублений, выступов) косым курсом. В этом случае на несущую систему действуют преимущественно кососимметричные нагрузки, вызывающие ее кручение относительно продольной оси КМ. Этот режим принимают как квазистатический в связи с тем, что движение осуществляется с минимальной скоростью и, следовательно, инерционными нагрузками пренебрегают.

В предельном случае при преодолении препятствий косым курсом возможен отрыв колеса (колес) от дороги. При этом нагрузки можно определить, исходя из условия статического равновесия: при l_п > 0,5L_M (см. рис. 1.2.1, б)

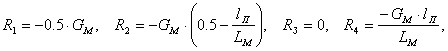
при l_п < 0,5L_M

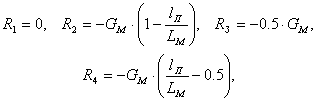
При вывешивании колес левого борта расчетные выражения для R₃ и R₄ аналогичны полученным для R₁ и R₂.

Совокупность этих нагрузок можно заменить суммой симметричных и кососимметричных сил, вызывающих изгиб и кручение несущей системы относительно продольной оси. Следует учитывать, что для КМ с числом осей больше двух возможно вывешивание нескольких колес в различных сочетаниях. Подобным этому режиму является режим поддомкрачивания КМ.

Для самосвалов к числу предельных режимов следует также отнести момент начала высыпания груза из грузовой платформы в двух вариантах: самосвал стоит на горизонтальной и наклонной поверхностях.

Наряду с квазистатическими нагрузками к категории предельных можно отнести и динамические нагрузки, возникающие при ударе и низкочастотном резонансе.

Нагрузки, возникающие при ударе, как правило, имеют короткое (импульсное) воздействие. Поэтому в наибольшей степени последствия такого воздействия проявляются в локальной зоне (удара).

В связи с этим данный режим рекомендуется использовать при уточненных расчетах и прежде всего расчете локальных зон.

В зависимости от микропрофиля дорожной поверхности, а также условий движения КМ могут возникать колебания с частотами, близкими к резонансным. Особенно опасны эти явления для несущих систем при частотах 0 ... 5 Гц. Если возникает резонанс, то возможны поломки элементов КМ, и в том числе несущей системы, вследствие чрезмерных (предельных) динамических нагрузок. Поэтому с целью предотвращения поломок важно исследовать возможность появления таких режимов.

Внешнее возмущение зададим в виде синусоиды, поскольку задачи определения напряженно-деформированного состояния несущих систем КМ решаются, как правило, в линейной постановке. Амплитуды возмущения и период колебаний должны соответствовать эксплуатационным (возможным неровностям дороги и скорости движения КМ).

Для упрощения расчетов примем, что неровности по обоим бортам одинаковые, контакт колеса с дорогой точечный, колеса движутся без пробуксовки и отрыва от дороги. Расстояние l между двумя максимумами зададим равным расстоянию между передней и задней осью (при этом можно добиться наибольшего эффекта воздействия на КМ), что не противоречит статистическим данным. Эквивалентную скорость (км/ч) движения КМ по дороге с указанными параметрами определяем по формуле

где f - собственная частота колебаний агрегата, Гц. Расчетным путем можно моделировать движение КМ по дороге со случайным характером микропрофиля и вычислять при этом динамические нагрузки, действующие на несущую систему.

Возмущение от микропрофиля можно задавать как ряд случайных нормально распределенных чисел с математическим ожиданием М = 0 и средним квадратическим отклонением, обусловленным определенным типом дороги. В результате можно определить нагрузки, действующие на несущую систему и соответствующие реальным (случайным).

кузов автомобиль конструкция моделирование