Навигация
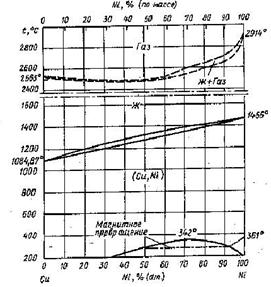
Расчёт купола расслаивания твёрдого раствора Cu–Ni
2.2 Расчёт купола расслаивания твёрдого раствора Cu–Ni
Для проверки адекватности модели, использованной при решении, а следовательно и правильности определения значений энергий смешения необходимо решить обратную задачу – по известным температурным зависимостям величин Q рассчитать координаты купола расслаивания и сравнить его со снятым с диаграммы состояния. Фактически, необходимо решить систему относительно x, N и T.
В соответствии с правилом фаз Гиббса, система Cu – Ni имеет одну степень свободы. Это означает, что только один из параметров x, N, T является независимым. Для однозначного решения необходимо задавать один параметр и, решая систему (2.8), находить остальные.
Для учёта зависимостей ![]() и
и ![]() от температуры необходимо провести аппроксимацию этих функций полиномами. В рамках этой работы было проверено два способа аппроксимации.
от температуры необходимо провести аппроксимацию этих функций полиномами. В рамках этой работы было проверено два способа аппроксимации.
Способ №1. Результаты аппроксимации зависимостей Q=f(T) представлены в таблице 2.3. Там же приведены значения полученных коэффициентов достоверности аппроксимации (квадратов коэффициентов корреляции).
Табл. 2.3. Аппроксимация зависимостей Q=f(T).
| Линия | Полином | R2 |
| 1 | Q = 33,285T - 17925 | 0,7556 |
| Q = -0,1902T2 + 237T - 72123 | 0,7885 | |
| Q = 0,0128T3 - 20,674T2 + 11166T - 2E+06 | 0,9489 | |
| Q = -0,0001T4 + 0,2512T3 - 211,76T2 + 79045T - 1E+07 | 0,9586 | |
| Q = -1E-05T5 + 0,0294T4 - 31,331T3 + 16641T2 - 4E+06T + 5E+08 | 1 | |
| 2 | Q = -31,278T + 29506 | 0,9218 |
| Q = 0,2428T2 - 291,32T + 98689 | 0,9959 |
Видно, что для линии 1 высоких значений R2 удаётся достичь только при больших степенях полинома. К сожалению, при этом не очень точно вычисляются их коэффициенты. К тому же, с такими зависимостями трудно работать. Всё это послужило причиной того, что от данного способа автор работы отказался.
Способ №2. Было принято решение разделить функции на три части соответствующие температурам ![]() для первой части,
для первой части, ![]() для второй и
для второй и ![]() для третьей (на рис. 2.1 эти части разделены вертикальными прямыми). На каждом из этих отрезков зависимость можно аппроксимировать полиномом меньшей степени. Результаты приведены в таблице 2.4.
для третьей (на рис. 2.1 эти части разделены вертикальными прямыми). На каждом из этих отрезков зависимость можно аппроксимировать полиномом меньшей степени. Результаты приведены в таблице 2.4.
Табл. 2.4. Аппроксимация частей зависимости Q=Q(T).
| Линия | Часть | Полином | R2 |
| 1 | 1 | Q = 76,812T - 39259 | 0,9437 |
| Q = -1,2995T2 + 1371,1T - 361006 | 1 | ||
| 2 | Q = -46,012T + 24707 | 1 | |
| 3 | Q = 51,263T - 28567 | 0,9981 | |
| Q = -0,1545T2 + 228,27T - 79216 | 1 | ||
| 2 | 1 | Q = -51,085T + 39360 | 0,9991 |
| Q = -0,1052T2 + 53,71T + 13310 | 1 | ||
| 2 | Q = -27,883T + 27204 | 1 | |
| 3 | Q = -13,086T + 19091 | 0,9994 | |
| Q = 0,0224T2 - 38,784T + 26444 | 1 |
Задав таким образом зависимости Q=f(T) как полиномы второй степени и зафиксировав один из параметров x, N, T, нужно решить систему (2.8). В этом случае система будет состоять из двух трансцендентных уравнений, и решить их совместно можно только численными методами. Автору работы не удалось этого сделать.
Поэтому было принято решение пожертвовать точностью аппроксимации функций Q=f(T) и определить их как линейные зависимости. В этом случае Q=aT+b и температура будет входить в уравнения системы (2.8) только в первой степени, что позволяет исключить её, как неизвестное.
Воспользуемся условными обозначениями, которые уже были использованы ранее.
Пусть ![]() , а
, а ![]() . Тогда первое уравнение системы (2.9) запишется в виде:
. Тогда первое уравнение системы (2.9) запишется в виде:
![]() (2.15)
(2.15)
Если перенести все слагаемые, содержащие Т, в левую часть, а все остальные – в правую часть уравнения, то получится:
![]()
![]() (2.16)
(2.16)
Осталось только выразить температуру в явном виде:
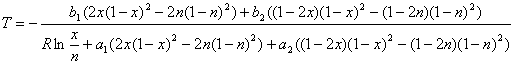 (2.17)
(2.17)
Аналогично нужно выразить температуру и из второго уравнения системы (2.9):
![]() (2.18)
(2.18)
![]()
![]() (2.19)
(2.19)
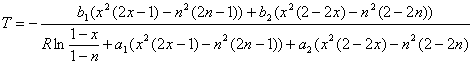 (2.20)
(2.20)
Приравняв правые части равенств (2.17) и (2.20) и умножив их на -1, приведём уравнение к окончательному виду:
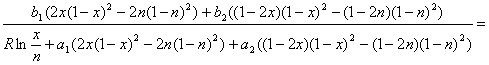
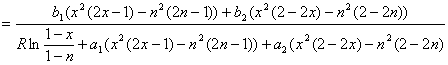 (2.21)
(2.21)
Параметра а и b определим из данных таблицы 2.4. Чтобы решить трансцендентное уравнение (2.21), нужно задаться одним из параметров x, или n и численными методами подобрать второй параметр, а затем определить и температуру по любому из уравнений (2.17) или (2.20).
Для решения была использована надстройка «поиск решения» пакета Microsoft Excel. Результаты решения представлены в таблице 2.5.
Табл. 2.5. Рассчитанный купол расслаивания твёрдого раствора при разных температурах
| t, oC | Состав α-фазы (Cu) | Состав γ-фазы (Ni) | ||
| x1 | x2 | N1 | N2 | |
| 0 | 0,727 | 0,273 | 2,8E-06 | 0,999997 |
| 25 | 0,723 | 0,277 | 0,000014 | 0,999986 |
| 40 | 0,72 | 0,28 | 0,000035 | 0,999965 |
| 83 | 0,71 | 0,29 | 0,00027 | 0,99973 |
| 116 | 0,70 | 0,30 | 0,001 | 0,999 |
| 141 | 0,69 | 0,31 | 0,002 | 0,998 |
| 161 | 0,68 | 0,32 | 0,004 | 0,996 |
| 178 | 0,67 | 0,33 | 0,007 | 0,993 |
| 191 | 0,66 | 0,34 | 0,010 | 0,990 |
| 203 | 0,65 | 0,35 | 0,014 | 0,986 |
| 241 | 0,60 | 0,40 | 0,042 | 0,958 |
| 261 | 0,55 | 0,45 | 0,061 | 0,939 |
| 279 | 0,50 | 0,50 | 0,077 | 0,923 |
| 307 | 0,45 | 0,55 | 0,128 | 0,872 |
| 322 | 0,40 | 0,60 | 0,174 | 0,826 |
| 331 | 0,35 | 0,65 | 0,224 | 0,776 |
| 334 | 0,30 | 0,70 | 0,273 | 0,727 |
| 334 | 0,285 | 0,715 | 0,285 | 0,715 |
Сравнение данных таблиц 2.1 и 2.5 можно провести визуально, нанеся данные на один график. Сравнение проведено на рисунке 2.2.

Рис. 2.2 Экспериментальный (1) и расчётный (2) купол расслаивания твёрдого раствора Cu – Ni
Из рисунка 2.2 видно, что экспериментальный и расчётный купол расслаивания твёрдого раствора Cu – Ni близки. По экспериментальным данным, критическая температура несмешиваемости равна 334°С.
Это позволяет говорить о том, что температурная зависимость Q=f(T) рассчитана правильно, и экстраполировать её до области комнатных температур.
Похожие работы
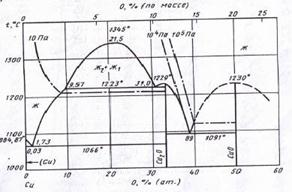
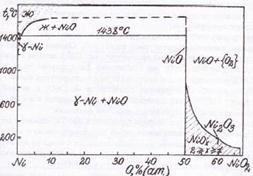
... VIII – CuO + NiO2 + {O2}. Области I и V очень малы и в масштабе диаграммы вырождаются в линии. Анализируя диаграмму Cu – Ni – O можно сделать следующие выводы о химической устойчивости медно-никелевых сплавов: 1) Окисление сплавов начинается уже при давлениях кислорода в газовой фазе над сплавами большем чем атм. Поэтому медно-никелевые сплавы будут окисляться кислородом воздуха при 25оС. 2) ...

0 комментариев