Навигация
Равноугольная (логарифмическая) спиральная антенна
85726
знаков
2
таблицы
37
изображений
1.3 Равноугольная (логарифмическая) спиральная антенна
Широкодиапазонность антенн такого вида основана на том, что если отношение линейных размеров излучателя к длине волны остается постоянным и излучающая структура полностью определяется ее полярными углами, то направленность антенны оказывается абсолютно независимой от частоты.
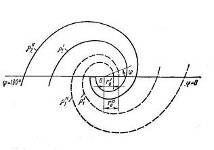
Рис.1.3.1. Логарифмическая спираль
Равноугольная спираль (рис. 1.3.1) строится в полярных координатах по уравнению
(1.3.1)
где 
— радиус-вектор в начале спирали (
); а — коэффициент, определяющий степень увеличения радиус-вектора с увеличением полярного угла 
.
Двухзаходная спираль образуется двумя проводниками или щелями, но в отличие от архимедовой спиральной антенны толщина их непостоянна и возрастает с увеличением угла 
. Пусть начальный радиус-вектор на внутренней границе 1-го проводника равен 
и на внешней
. Тогда уравнениями граничных спиралей являются
(1.3.2)
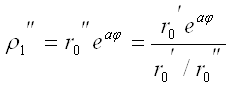. (1.3.3)
Для оценки диапазонности логарифмической спирали исследуем зависимость отношения 
от угла 
. Числитель дроби 
,а так как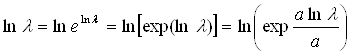 
,
то знаменатель дроби и искомое отношение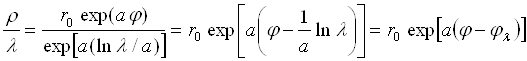 
,(1.3.4)
где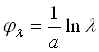 
. Следовательно, изменение длины волны вызывает только смещение активной области спирали на некоторый угол 
, а отношение 
и направленное действие антенны от этого не меняются. Если бы спираль была бесконечной, то диапазонность антенны была безграничной, но реальная антенна имеет конечную
длину и эффективно работает в ограниченном, хотя и очень широком диапазоне волн 
,причем 
определяется максимальной длиной спирали, а 
— минимальными размерами узла питания.
4.3. Логарифмическая спираль работает в режиме бегущих волн (вследствие излучения ток затухает к концу спирали), и ее входное сопротивление 
Ом.
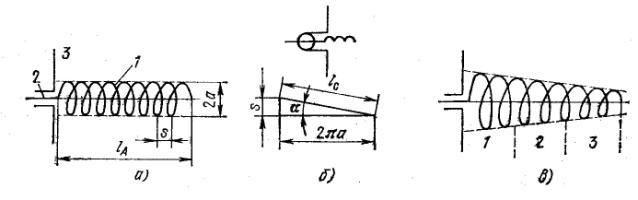
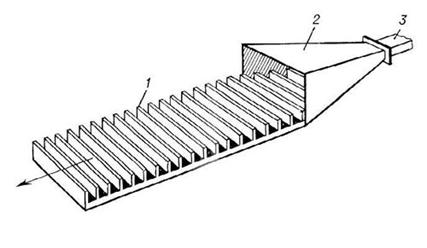
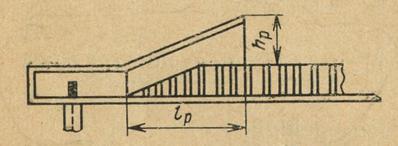
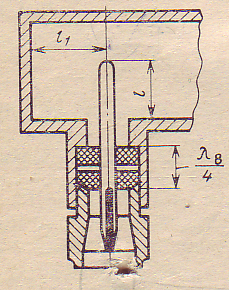
Рис.1.3.2. Щелевая плоская логарифмическая спиральная антенна
Типовая щелевая логарифмическая спираль (рис. 6) имеет максимальную длину ветви 42,3 см, начальный радиус 0,51 см и коэффициент 
= 0,303. Антенна излучает волны с вращающейся поляризацией в диапазоне 
см и 
не превышает двух при питании спирали от 50-Ом коаксиального кабеля. Параметры антенны находятся в допустимых пределах даже при двадцатикратном изменении длины волны.
1.4 Коническая спиральная антенна
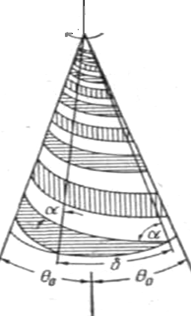
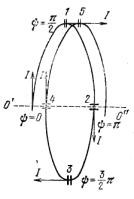
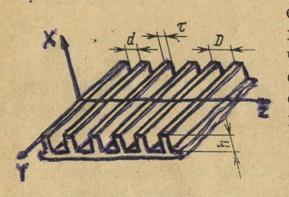
Коническая спиральная антенна (рис.1.4.1) состоит из двух металлических полосок, расположенных на поверхности конуса θ=θ0, конфигурация которых дается уравнением
θ=1800
θ=0
Рис.1.4.1 Коническая спиральная антенна
Угол 
между радиусом и касательной к спирали равен arctg а. Таким образом, плоская спираль есть частный случай конической при θ = 900.
В случае конуса можно говорить о самодополнительной структуре, имея в виду идентичность участков поверхности конуса, покрытых полоской и свободных от нее. Положение тех и других отличается на угол поворота 900; иначе говоря, ширина ветви δ на рис.1 равна 900. Оказывается, что самодополнительная структура обеспечивает наилучшую диаграмму направленности. Переход к конической форме позволяет выявить одну важную особенность спиральных антенн, которая не могла быть обнаружена при плоской форме спирали: излучение происходит за счет волны, перемещающейся внутрь по направлению к внешней спирали.
Глава 2. Свойства спиральных антенн
Похожие работы
... формулы: ширина диаграммы направленности , (5) коэффициент направленного действия , (6) входное сопротивление , (7) 2.4. Итак, цилиндрические и конические спиральные антенны широкополосные с осевым излучением волн круговой поляризации. Направленность цилиндрических спиралей средняя, а конических — ниже ...
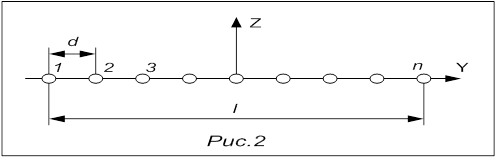
... на значении рабочей частоты и длине антенной решетки, которые являются, исходными данными для расчета вычисляем параметры одиночной спиральной антенны и ее ДН. После этого используя значения угла сканирования и уровня боковых лепестков, вычисляется количество излучателей решетки, расстояние между ними, а также ДН множителя решетки. После этого вычисляется ДН линейной антенной решетки. Расчет ...
... конусной части линии, должно быть: (7) [л.3.стр159] где: -волновое сопротивление конусной части перехода -волновое сопротивление подводящего фидера 75 Ом -волновое сопротивление спиральной антенны Ом По известному волновому сопротивлению можно определить отношение диаметров элементов коаксиального тракта: lg ( Ом ) (8) Для коаксиального устройства с воздушным заполнением и Ом ...
... могут поддерживать либо волны Е, либо волны Н, либо те и другие, отличающихся конструктивным выполнением и формой поверхности. Антенны с плоскими и_цилиндрическими непрерывными замедляющими структурами называют антеннами поверхностных волн. Примерами антенн с замедленной фазовой скоростью являются: диэлектрические стержневые антенны, спиральные антенны, антенны «волновой канал», различные виды ...
0 комментариев