ПОДБОР ПОДШИПНИКОВ ДЛЯ ВАЛОВ РЕДУКТОРА

8. ПОДБОР ПОДШИПНИКОВ ДЛЯ ВАЛОВ РЕДУКТОРА

 

Из расчетов и компоновки: F_t=1750 Н, F_r=660 Н, F_а=481 Н, l₁=l₂=55 мм,

d₁=37,33 мм, d₂= 186,67 мм.

Ведущий вал

Определяем предварительно консольную нагрузку от муфты, действующую на выходном конце вала (табл. 6.2./2/):

F_м=80=80 =466 Н

Принимаем l_м=65 мм.

Вычерчиваем расчетную схему нагружения вала (рис.7.1) Опору, воспринимающую внешнюю осевую силу обозначаем символом 2.

Определяем опорные реакции в горизонтальной плоскости хz от силы F_t:

Н;

Строим эпюру изгибающих моментов относительно оси У в характерных сечениях:

М_У1= М_УА= М_У2=0; М_УВ= R_1Хּ l₁ = 875·0,055=48 Нּм

Определяем опорные реакции в вертикальной плоскости хy от сил F_rи F_а:

∑ М_Х1=0; R_2yּ 2 l₁ - F_rּ l₁ - F_а= 0,

∑ М_Х2=0; - R_1yּ2l_{1 +} F_rּ l₁ – F_а = 0,

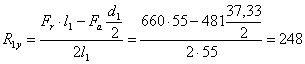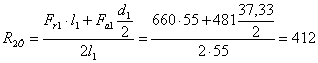 Н.

 Н,

Проверка:

∑F_y=0; R_2У + R_1У - F_r1 = 248+412−660= 0.

Строим эпюру изгибающих моментов:

М_Х1=М_Х2=0; М_ХВ^Л =R_1y l₁ =248 ּ0,055=13,6 Нּм;

М_ХВ^л = R_1yּ l₁ + F_а·d₁/2=248ּ0,054 +481·0,03733/2=22,7 Нּм

 

Определяем реакции опор от силы F_м:

∑М₁=0; - F_мּl_м + R_2мּ2ּl₁ =0;

∑М₂=0; - F_м(l_м+2ּl₁)+R_1мּ2ּl₁=0;

 Н;Н.

Проверка:

∑Х=0; R_1м+ F_м – R_2м= 466+275 –741= 0.

Строим эпюру изгибающих моментов М_Fм в характерных сечениях:

М_А= М₁=0; М₂= F_м ּ l_м = 466ּ0,065= 30,2 Нּм;

М_В = F_рּ(l_р+ l₁)−R_1м ּl₁= 466ּ(0,065+ 0,055)−741 ּ0,055= 15,1 Нּм

Строим эпюру крутящих моментов: М_к=Т₁=34 Нּм.

Определяем суммарные радиальные опорные реакции. Так как направление действия силы F_м неизвестно, то принимаем случай, когда реакции от действия силы F_м совпадают по направлению с суммарными реакциями опор от действия силы в зацеплении зубчатой передачи:

 Н,

 Н.

Для принятого подшипника 207 С_r=25,5 кН и С₀=13,7 кН

Определяем отношение R_а/С_о=481/13700=0,035 (коэффициент осевого нагружения е=0,24 по табл.9.2 /2/). Для подшипника 2, воспринимающего внешнюю осевую нагрузку отношение R_а/R_r2=481/1242=0,387 > е=0,24, то принимаем коэффициент радиальной нагрузки Х=0,56 и коэффициент осевой нагрузки Y=1,92.

Принимаем коэффициенты:

V=1 – коэффициент вращения внутреннего кольца подшипника;

К _δ =1,2 – коэффициент безопасности при легких толчках (табл. 9.4 /2/);

К _τ =1 – коэффициент температурныйt<100ºC (табл. 9.5. /2/).

Определяем эквивалентные нагрузки:

R_{e 2}=(R_r2ּVּХ+ R_аּY)ּК _δ ּК _τ =(1242·1ּ0,56+ 481ּ1,92)1,2 ּ1=1943 H

R_e1=R_r1·VּК _δ ּК _τ =1651∙1∙1,2 ּ1=1981 H.

Определяем расчетную долговечность наиболее нагруженного подшипника 1:

20ּ10³ ч,

ч.

Долговечность подшипников соблюдается.

Ведомый вал

Силу от цепной передачи раскладываем на составляющие:

F_{цеп Г} =F_цеп·cos 60º=1995•0,5=998 H

F_{цеп В} =F_цеп·sin 60º=1995•0,866=1728 H

Принимаем l_ц=50 мм.

Вычерчиваем расчетную схему нагружения вала (рис. 7.2,) Опору, воспринимающую внешнюю осевую силу обозначаем символом 4.

Определяем опорные реакции от силы F_t и F_{цеп Г} в горизонтальной плоскости:

∑ М₄=0; R_Г32 l₂+F_t ·l₂−F_{цеп Г})2·l₂ + l_ц)= 0,

∑ М₃ =0; R_Г42l₂ −F_t l₂−F_{цеп Г} l_ц= 0,

Проверка

∑X= F_t +R_Г3−R_Г4−F_{цеп Г} =1750+577−1329−998=0

Строим эпюру изгибающих моментов относительно оси У в характерных сечениях:

М_УД= М_У4=0; М_УС= −R _Г4• l₂ = −1329•ּ0,055=−73,1 Нּм

M_y6=−F_{цеп В} l_ц =−998•0,05=−49,9 Н•м

Определяем опорные реакции в вертикальной плоскости от сил F_{цеп Г}, F_rТ и F_аТ.

∑ М₃=0 ; R_4В•2 l₂ −F_r l₂−F_{цеп В} l_ц −F_а•d₂/2 –= 0,

∑ М₄ =0 ; R_3В•2 l₂ +F_r l₂− F_{цеп В}) 2 l₂ + l_ц) −F_а•d₂/2 = 0,

Проверка

∑Y= R_4В−R_3В+ F_{цеп В} – F_r=1523−2591+1728−660=0

Строим эпюру изгибающих моментов относительно оси Х в характерных сечениях:

М_ХД= М_Х4= 0; М^л_ХС= R_4Вּ l₂ =1523•0,055= 83,76 Нּм

М^п_ХК= R_4Вּ l₂ - F_а•d₄/2 =1523•0,055−481•0,18667/2= 38,87 Нּм

M_X6 = F_{цеп Г} ּl_ц =1728·0,05=86,4 Н•м

Строим эпюру крутящих моментов: М_к=Т₂=163,3 Нּм.

Определяем суммарные радиальные опорные реакции:

 Н,

 Н.

Для принятого подшипника 209 С_r=33,2 кН и С₀=18,6 кН

Определяем отношение R_а/С_о=481/18600=0,026 (коэффициент осевого нагружения е=0,22 по табл.9.2 /2/). Так как отношение R_а/R_r4= =481/2021=0,24>е=0,22, то принимаем коэффициент радиальной нагрузки Х=0,56 и коэффициент осевой нагрузки Y=2,02.

Принимаем коэффициенты:

V=1; К _δ =1,2; К _τ =1.

R_e3=R_r3ּVּХּ К _δ ּК _τ = 2655ּ1ּ1,2 ּ1=3186 H,

R_e4=(R_r4ּVּХ+ Y ∙ F_а)·К _δ ּК _τ =(2021·1∙0,56+2,02·481)∙1,2 ּ1=2524 H

Определяем расчетную долговечность наиболее нагруженного подшипника 3:

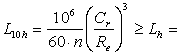30ּ10³ ч,

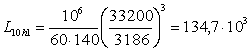ч.

Долговечность подшипников соблюдается.