Критерий, основанный на определении длины фазы

2.   Критерий, основанный на определении длины фазы

Интервал между двумя поворотными точками называется фазой. Для того , чтобы установить наличие фазы длины d (например, восходящей) , нужно обнаружить d+3 членов, содержащих падение от первого члена ко второму ,затем последовательный подъем до (d+2)-го члена и падение к (d+3)-ему члену.

 

 

 

1 2 3 4 d+1 d+2 d+3 N

рис. 3. Фаза длины d.

Рассмотрим группу из d+3 чисел, расположенных в порядке возрастания. Если, не трогая двух крайних членов, извлечь пару чисел из оставшихся d+1 и одно из них поставить в начало, а другое в конец, получим фазу длины d. Существует  способов такого выбора пары чисел и каждый член пары может быть поставлен в любой конец, следовательно число восходящих фаз равно d(d+1).

Кроме того, поворотные точки будут иметь место, если первый член последовательности поставить в конец, а любой из оставшихся, за исключением второго, поместить в начало. Число таких последовательностей составит (d+1) . Еще столько же последовательностей получиться если последний член в исходной, возрастающей, последовательности поставить в начало, а любой другой, кроме последнего, в конец. Во избежании двойного счета следует исключить случай, когда первый член ставится на последнее место, а последний на первое. Таким образом, в последовательности из (d+3) чисел с фазой длиной d число случаев роста составит

 

d(d+1)+2(d+1)-1 =+3d+1 .

Число возможных последовательностей из (d+3) чисел равняется числу перестановок (d+3)!, так что вероятность либо восходящей, либо нисходящей фазы равна

 

.

В ряде длины N последовательно можно выделить N-2-d групп по d+3 членов. Т.о. математическое ожидание числа фаз длины d

.

Можно показать, что математическое ожидание общего числа фаз длины от 1 до N-3

 

.

 

3.Критерий , основанный на знаках разностей

Данный критерий состоит в подсчете числа положительных разностей первого порядка в ряде , иначе говоря, числа точек возрастания ряда. Для ряда из N членов получаем N-1 разностей . Определим счетную переменную как

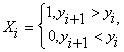
Если теперь обозначить через с число точек возрастания случайного ряда , то

.

Распределение довольно быстро стремится к нормальному с дисперсией

.

В основном данный критерий рекомендуется для проверки наличия линейного тренда . С другой стороны, критерий, основанный на поворотных точках , плохо подходит для обнаружения тренда, т.к. наложение заметных случайных колебаний на умеренный тренд приводит примерно к тому же множеству поворотных точек, что и при отсутствии тренда. .Более совершенным, но более сложным критерием для обнаружения линейного тренда являются регрессия y на t и проверка значимости регрессионного коэффициента.

4.Критерий, основанный на ранговых сравнениях

Идею сравнения соседних значений ряда можно развить до сравнения всех значений. Для данного ряда подсчитаем число случаев, когда очередной член ряда превышает все последующие. Всего для сравнения имеется N(N-1) пар. Пусть n общее число случаев превышения. Подсчитывают ранговый коэффициент корреляции Кендэла

 

.

Если этот коэффициент значим и положителен, то ряд возрастающий, если отрицателен, то - убывающий.

10.Теоретический анализ стационарной случайной составляющей линейного вида

Рассматривается общая линейная модель стохастического процесса

, (1)

где  – белый шум

 – весовые коэффициенты.

Напомним, что=0, ,

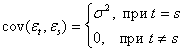
Введем оператор сдвига на один шаг назад В:

Многократное (для определенности j-кратное) применения оператора В, обозначаем как , дает  С учетом введенных обозначений общую линейную модель можно записать как

 ( )

где – линейный оператор.

Найдем математическое ожидание, дисперсию и автоковариационную функцию для процесса (1):

;

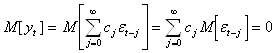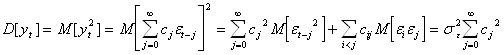
Для того чтобы модель имела смысл, дисперсия  должна быть конечной, то есть предполагается, что ряд  сходится.

Кроме этого предполагают, что имеет место так называемое условие обратимости:

,

где вместо В фигурируют комплексные числа. Из этого условия вытекает существование обратного оператора

,

где , то есть такого, что

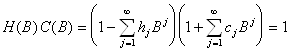
Раскрывая произведение в последнем выражении, группируя однородные по  члены и приравнивая их к нулю, получают выражения для определения коэффициентов  . Так,  и так далее.

Умножая () на  слева, получим, что обратимый процесс может быть записан в виде

,

или

 (2)

Запись (2) соответствует авторегрессионой схеме бесконечного порядка. Это же соотношение можно трактовать как линейный предиктор для по всем прошлым значениям временного ряда, а слагаемое  – как случайную ошибку этого предиктора. Если известны все прошлые значения ряда, то по форме (2) можно спрогнозировать будущее значение ряда.

  10.1\. Модели авторегрессии

Рассмотрим более подробно модели случайной составляющей, являющиеся частными случаями общей линейной модели, а именно модели авторегрессии, скользящего среднего и смешанные, широко применяемые на практике.

  10.1.1 Авторегрессия первого порядка (марковский процесс)

Модель АР(1) имеет вид

.

С использованием оператора сдвига В модель примет вид

.

Отсюда

Рассматривая  как сумму бесконечно убывающей геометрической прогрессии со знаменателем а В получаем, что

 (2)

Таким образом, марковский процесс есть частный случай общей линейной модели, коэффициенты которой меняются по закону геометрической прогрессии, то есть .

Выражение (2) можно получить и из (1) непосредственно, выражая  через ,  через  и т.д.

Дисперсия  в соответствие с () есть

Выходит, белый шум с дисперсией  порождает в схеме Маркова случайный процесс с возросшей дисперсией, равной .

Для нахождения автоковариационной функции Марковского процесса можно воспользоваться общим выражением ( ). Однако более нагляден следующий путь. Домножим уравнение (1) марковского процесса на и возьмем математическое ожидание

.

Поскольку второе слагаемое в правой части равно нулю в силу некоррелированности возмущения  в текущий момент с прошлыми значениями ряда , получаем

( в силу стационарности )

Из последнего соотношения имеем

,

то есть а совпадает с коэффициентом автокорреляции  средних членов ряда. Умножим теперь (1) на  и возьмем математическое ожидание:

.

Заменяя а на  и деля на  , получаем

.

Придавая k значения 2,3,… получим

.

Итак, в марковском процессе все автокорреляции можно выразить через первую автокорреляцию. Поскольку , автокорреляционная функция марковского процесса экспоненциально убывает при росте k.

Рассмотрим теперь частную автокорреляционную функцию марковского процесса. Мы получили, что корреляция между двумя членами ряда, отстоящими на два такта, то есть между  и  выражается величиной . Но  зависит от , а  от . Возникает вопрос, сохранится ли зависимость между  и , если зависимость от срединного члена  устранена. Соответствующий частный коэффициент корреляции есть

.

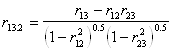Поскольку , числитель равен нулю. Аналогично можно показать, что частные коэффициенты корреляции для членов ряда, отстоящих на 3,4 и так далее тактов, также равны нулю. Таким образом, автокорреляция существует только благодаря корреляции соседних членов, что впрочем следует из математической модели марковского процесса.

Завершая рассмотрение модели АР(1), отметим, что она весьма часто используется в экономико-математических исследованиях для описания остатков линейной регрессии, связывающей экономические показатели.

  Авторерессия второго порядка (процесс Юла)

Авторегрессионный процесс Юла АР(2) описывается уравнением

 (1)

С использованием оператора сдвига В модель запишется как

,

где а(В) – авторегрессионный оператор, то есть а(В)= .

Свойства модели зависят от корней  и  полинома

=0, (2)

который можно записать также в виде

(1-В)(1-В)=0.

Для стационарности процесса (1) необходимо, чтобы корни  и  лежали внутри единичной окружности (случай комплексных корней), либо были меньше единицы (случай действительных корней), что обеспечивается при  .

Пусть  и  действительны и различны. Разложим на простые дроби

, (3)

где .

Рассматривая отдельные слагаемые в (3) как суммы бесконечных геометрических прогрессий, получим

.

Выходит АР(2) есть частный случай общей линейной модели ( ) с коэффициентами

.

Рассмотрим теперь автокорреляционную функцию процесса Юла. Умножим (1) по очереди на  и , возьмем математические ожидания и разделим на . В итоге получим

Этих уравнений достаточно для определения  через первые две автокорреляции и, наоборот, по известным  можно найти .

Умножая теперь (1) на  получим рекуррентное уравнение

, (4)

из которого можно найти автокорреляции высоких порядков через первые автокорреляции. Тем самым, полностью определяется коррелограмма процесса Юла.

Исследуем вид коррелограммы процесса АР(2).

Выражение (4) можно рассматривать как разностное уравнение второго порядка относительно r с постоянными коэффициентами.

Общее решение такого уравнения имеет вид

,

где  – корни характеристического уравнения

 (5)

Легко видеть, что уравнения (2) и (5) эквивалентны с точностью до замены В на z и деления обоих частей на , так что корни этих уравнений совпадают, то есть

Общее решение разностного уравнения (4) есть

 (6)

где коэффициенты А и В находят из граничных условий при j=0 и j=1.

Таким образом, в случае действительных корней коррелограмма АР(2) представляет собой, как видно из (6), смесь двух затухающих экспонент.

В случае комплектности корней  и  коррелограмма процесса АР(2) оказывается затухающей гармоникой.

Рассмотрим теперь как ведет себя частная автокорреляционная функция процесса Юла. Отличным от нуля оказывается лишь коэффициент  , равный . Частные корреляции более высоких порядков равны нулю (подробнее этот процесс рассматривается дальше). Таким образом, частная коррелограмма процесса отрывается сразу после лага, равного единице.

В заключении отметим, что модели АР(2) оказались приемлемыми при описании поведения циклической природы, прообразом которого служит маятник, на который воздействуют малые случайные импульсы. Амплитуда и фаза такого колебательного процесса будут все время меняться.

10.1.3. Авторегрессия порядка р

Процесс авторегрессии порядка р, кратко АР(р), описывается выражением

 (1)

или

 ( )

Решение разностного относительно y выражения (1) или () состоит из двух частей: общего решения, содержащего р произвольных констант, и частного решения. Общее решение есть

, (2)

где – есть постоянные коэффициенты,

 (j=1,2,...,р) – корни характеристического уравнения.

 (3)

Стационарность ряда (2) имеет место, если корни уравнения (3) имеют модуль меньше единицы. Другими словами, корни должны лежать внутри единичного круга. Считая, что ряд имеет достаточно длинную предысторию, общим решением (2) можно пренебречь вследствие затухания.

Частое решение, как видно из (), есть

Последнее соотношение есть форма представления авторегрессионного процесса в виде общей линейной модели.

Последовательно умножим уравнение (1) на , возьмем математическое ожидание и разделим на . Получим систему уравнений относительно коэффициентов корреляции :

, k=1, 2, ..., p (4)

Учитывая, что  , и вводя матричные обозначения

,

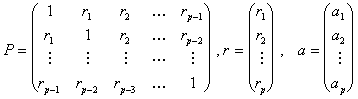запишем (4) в виде

 

Pa=r (5)

Систему уравнений (5) называют системой Юла-Уокера. Из нее находим, что

 

a=r (6)

Таким образом, зная первые р автокорреляций временного ряда, можно найти по (3) автокорреляции более высокого порядка, то есть полностью восстановить автокорреляционную функцию (что уже отмечалось при анализе процессов АР(1) и АР(2)).

Поведение автокорреляционной функции зависит от корней характеристического полинома. Обычно коррелограмма процесса АР(р) состоит из совокупности затухающих синусоид.

Если у процесса АР(2) частная автокорреляция членов ряда, разделенных 2-мя или большим числом членов, равна нулю, то у процесса АР(р) нулю равны автокорреляции порядка р и выше. Выходит, частная коррелограмма процесса АР(р) должна равняться нулю, начиная с некоторого момента. Правда, надо заметить, что этот факт имеет место для бесконечного ряда. Для конечных реализаций указать место обрыва коррелограммы часто затруднительно.

Итак, для процесса АР(р) частная автокорреляционная функция обрывается на лаге р, тогда как автокорреляционная функция плавно спадает.

  10.1.4 Процессы скользящего среднего

Обобщенная линейная модель для процессов скользящего среднего содержит лишь конечное число членов, то есть в ( ): =0 k> q .

Модель приобретает вид

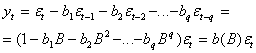 (1)

(В (1) коэффициенты  переобозначены через.)

Соотношение (1) определяет процесс скользящего среднего порядка q, или сокращенно СС(q). Условие обратимости ( ) для процесса СС(q) выполняется, если корни многочлена b(В) лежат вне единичного круга.

Найдем дисперсию процесса СС(q):

Все смешанные произведения вида  равны нулю в силу некоррелированности возмущений в разные моменты времени. Для нахождения автокорреляционной функции процесса СС(q) последовательно умножим (1) на и возьмем математическое ожидание

 (2)

В правой части выражения (2) останутся только те члены, которые отвечают одинаковым временным тактам (см. рис )

     

    (k=2)

Следовательно, выражение (2) есть

 (3)

поделив (3) на  , получим

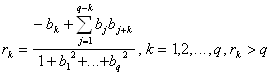 (4)

Тот факт, что автокорреляционная функция процесса СС(q) имеет конечную протяженность (q тактов) – характерная особенность такого процесса. Если  известны, то (4) можно в принципе разрешить относительно параметров . Уравнения (4) нелинейные и в общем случае имеют несколько решений, однако условие обратимости всегда выделяет единственное решение.

Как уже отмечалось, обратимые процессы СС можно рассматривать как бесконечные АР- процессы -АР(¥). Следовательно, частная автокорреляцонная функция процесса СС(р) имеет бесконечную протяженность. Итак, у процесса СС(q) автокорреляционная функция обрывается на лаге q, тогда как частная автокорреляционная функция плавно спадает.

  10.1.5 Комбинированные процессы авторегрессии - скользящего среднего

Хотя модели АР(р) и СС(q) позволяют описывать многие реальные процессы, число оцениваемых параметров может оказываться значительным. Для достижения большей гибкости и экономичности описания при подборе моделей к наблюдаемым временным рядам весьма полезными оказались смешанные модели, содержащие в себе и авторегрессию и скользящее среднее. Эти модели были предложены Боксом и Дженкинсом и получили название модели авторегрессии - скользящего среднего (сокращенно АРСС(р, q)):

 (1)

С использованием оператора сдвига В модель (1) может быть представлена более компактно:

, ( )

где а(В)—авторегрессионный оператор порядка р,

b(В)—оператор скользящего среднего порядка q.

Модель () может быть записаны и так :

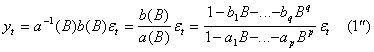
Рассмотрим простейший смешанный процесс АРСС(1,1)

Согласно

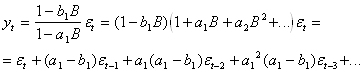 (2)

Из соотношения (2) видно, что модель АРСС(1,1) является частным случаем общей линейной модели ( ) с коэффициентами  (j>0)

Из (2) легко получить выражение для дисперсии :

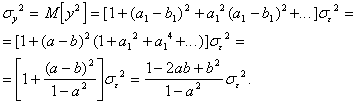
Для получения корреляционной функции воспользуемся тем же приемом, что и при анализе моделей авторегрессии. Умножим обе части модельного представления процесса АРСС(1,1)

на  и возьмем математическое ожидание :

или (с учетом того, что второе слагаемое в правой части равенства равно нулю)

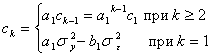
Поделив ковариации  на дисперсию  получаем выражения для автокорреляции

полученные соотношения показывают, что  экспоненциально убывает от начального значения  , зависящего от  и  при этом, если  > , то затухание монотонное; при <  – затухание колебательное.

Аналогично может быть построена автокорреляционная функция для общей модели АРСС(р, q).

Умножим все члены (1) на . Возьмем математическое ожидание и в результате получим следующее разностное уравнение.

Где  - взаимная ковариационная функция между y и . Поскольку возмущения  в момент t и значения ряда в прошлые моменты (см(2)) не коррелируют,