При k>0

0 при k>0.

Отсюда следует, что для значений q+1 автоковариации и автокорреляции удовлетворяют тем же соотношениям, что и в модели АР(р):

В итоге оказывается, что при q<р вся автокорреляционная функция будет выражаться совокупностью затухающих экспонент и / или затухающих синусоидальных волн, а при q>p будет q-p значений , выпадающих из данной схемы.

  10.1.6 Интегрированная модель авторегрессии- скользящего среднего

Модель АРСС допускает обобщение на случай, когда случайный процесс является нестационарным. Ярким примером такого процесса являются «случайные блуждания»:

 (1)

С использованием оператора сдвига модель (1) принимает вид

 (2)

Из (2) видно, что процесс (1) расходящийся, поскольку. Характеристическое уравнение этого процесса имеет корень, равный единице, то есть имеет место пограничный случай, когда корень характеристического уравнения оказался на границе единичной окружности. В то же время, если перейти к первым разностям , то процесс  окажется стационарным.

В общем случае полагается, что нестационарный авторегрессионный оператор  в модели АРСС имеет один или несколько корней, равных единице. Иными словами,  является нестационарным оператором авторегрессии порядка p+d; d корней уравнения =0 равны единице, а остальные р корней лежат вне единичного круга. Тогда можно записать, что

,

где a(B) – стационарный оператор авторегрессии порядка р (с корнями вне единичного круга).

Введем оператор разности , такой что =(1-B) , тогда нестационарный процесс АРСС запишется как

, (3)

где b(B) – обратимый оператор скользящего среднего (вне его корни лежат вне единичного круга).

Для разности  порядка d , то есть  модель

описывает уже стационарный обратимый процесс АРСС(р, q).

Для того чтобы от ряда разностей вернуться к исходному ряду требуется оператор s, обратный  :

Этот оператор называют оператором суммирования, поскольку

 .

Если же исходной является разность порядка d, то для восстановления исходного ряда понадобится d - кратная итерация оператора s, иначе d- кратное суммирование (интегрирование). Поэтому процесс (3) принято называть процессом АРИСС, добавляя к АРСС термин интегрированный. Кратко модель (3) записывают как АРИСС(р, d, q), где р – порядок авторегрессии, d – порядок разности, q – порядок скользящего среднего. Ясно, что при d =0 модель АРИСС переходит в модель АРСС .

На практике d обычно не превышает двух, то есть d .

Модель АРИСС допускает представление, аналогичное общей линейной модели, а так же в виде «чистого » процесса авторегрессии (бесконечного порядка). Рассмотрим, к примеру, процесс АРИСС (1, 1, 1):

 (4)

Из (4) следует, что

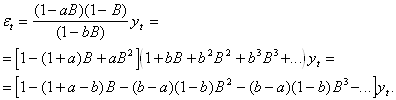
Отсюда

 (5)

В выражении (5) коэффициенты, начиная с третьего, вычисляются по формуле .

Представление (5) интересно тем, что веса, начиная с третьего, убывают по экспоненциальному закону. Поэтому, хотя формально зависит от всех прошлых значений, однако реальный вклад в текущее значение внесут несколько «недавних» значений ряда. Поэтому уравнение (5) более всего подходит для прогнозирования.

11.Прогнозирование по модели АРИСС

Как уже отмечалось, процессы АРИСС допускают представление в виде обобщенной линейной модели, то есть

Естественно искать будущее (прогнозное) значение ряда в момент  в виде

Ожидаемое значение , которое мы будем обозначать как

=

Первая сумма в правой части последнего соотношения содержат лишь будущие возмущения (прогноз делается в момент t, когда известны прошлые значения и ряда  и возмущений) и для них математическое ожидание равно 0 по определению. Что же касается второго слагаемого, то возмущения здесь уже состоялись, так что

Таким образом

= (1)

Ошибка прогноза, представляющая расхождение между прогнозным значением и его ожиданием есть

=

Дисперсия ошибки отсюда есть

 (2)

Прогнозирование по соотношению (1) в принципе возможно, однако затруднительно поскольку требует знания всех прошлых возмущений. К тому же для стационарных рядов скорость затухания  часто оказывается недостаточной, не говоря уже о нестационарных процессах, для которых ряды  расходятся.

Поскольку модель АРИСС допускает и другие представления, рассмотрим возможности их использования для прогнозирования. Пусть модель задана непосредственно разностным уравнением

 (3)

По известным значениям ряда (результатам наблюдений)  и оцененным значениям возмущений  , опираясь на рекуррентную формулу (3) можно оценить ожидаемое значение ряда в момент t+1:

-, (4)

При прогнозировании на два такта следует вновь воспользоваться рекуррентным соотношением (3), где в качестве наблюденного значения ряда в момент t+1 следует взять предсказанную по (4) величину , то есть  и так далее.

Наконец, возможно прогнозирование опираясь на представление процесса АРИСС в виде авторегрессии (). Как уже отмечалось, несмотря на то что порядок авторегрессии бесконечен, весовые коэффициенты в представлении ряда убывают довольно быстро, поэтому для вычисления прогноза достаточно умеренное число прошлых значений ряда.

Дисперсия ошибки прогноза на  шагов вперед есть

и согласно выражению (2) дается выражением

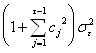
В предположении, что случайные возмущения являются гаусовским белым шумом, то есть  можно рассматривать доверительный интервал для прогнозного значения ряда стандартным образом.

12.Технология построения моделей АРИСС

Описанные выше теоретические схемы строились в предположении, что временной ряд имеет бесконечную предысторию, тогда как реально исследователю доступен ограниченный объем наблюдений. Модель приходится подбирать экспериментально, подгоняя ее к имеющимся в распоряжении данным. Поэтому с позиций теоретического применения теории анализа временных рядов определяющее значение имеют вопросы корректной спецификации модели АРИСС(p, d, q) (ее идентификации) и последующего оценивания ее параметров.

На этапе идентификации наблюденные данные используются для определения подходящего класса моделей и делаются предварительные оценки ее параметров, то есть строится пробная модель. Затем пробная модель подгоняется к данным более тщательно; при этом первичные оценки, полученные на этапе идентификации выступают в качестве начальных значений в итеративных алгоритмах оценивания параметров. И наконец, на третьем этапе полученная модель подвергается диагностической проверке для выявления возможной неадекватности модели и выработки подходящих изменений в ней.Рассмотрим перечисленные этапы подробнее.

 

Идентификация модели

Цель идентификации – получить некоторое представление о величинах p, d, q и о параметрах модели. Идентификация модели распадается на две стадии

1.   Определение порядка разности d исходного ряда .

2.   Идентификация модели АРСС для ряда разностей .

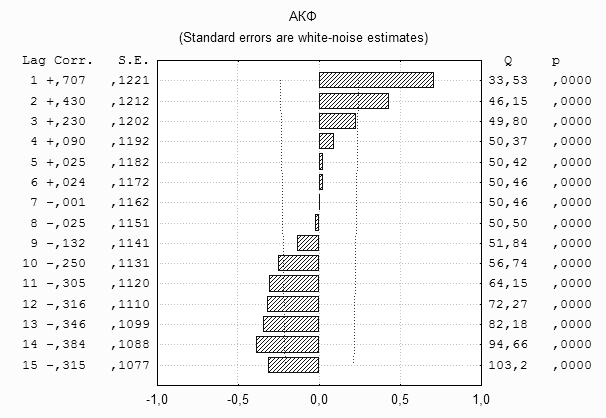
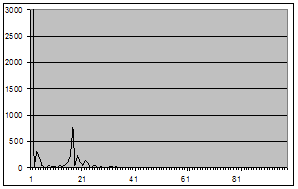
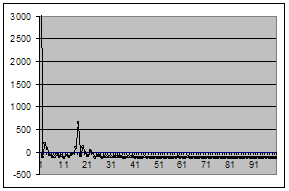
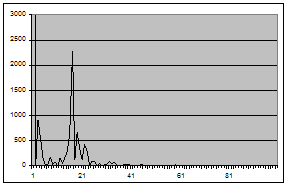
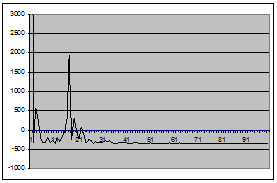
Основной инструмент, используемый на обеих стадиях – автокорреляционная и частная автокорреляционная функции.

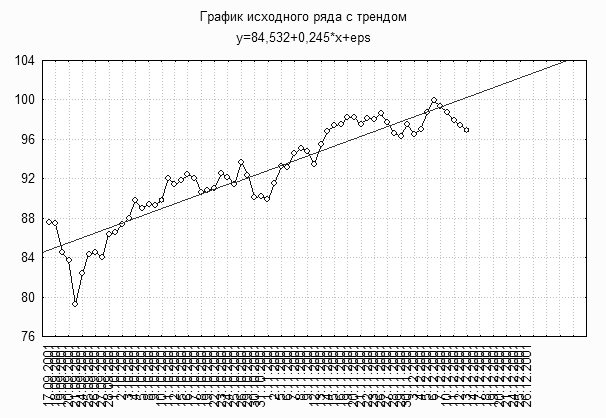
В теоретической части мы видели, что у стационарных моделей автокоррелящии  спадают с ростом k весьма быстро (по корреляционному закону). Если же автокорреляционная функция затухает медленно и почти линейно, то это свидетельствует о нестационарности процесса, однако, возможно, его первая разность стационарно.

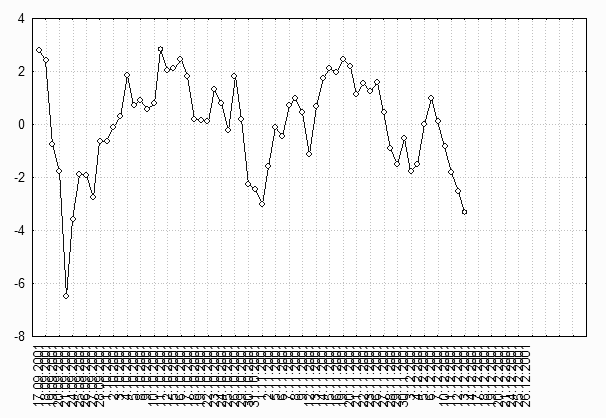
Построив коррелограмму для ряда разностей, вновь повторяют анализ и так далее. Считается, что порядок разности d, обеспечивающий стационарность, достигнут тогда, когда автокорреляционная функция процесса  падает довольно быстро. На практике  и достаточно просмотреть порядка 15-20 первых значений автокорреляции исходного ряда, его первые и вторые разности.

После того как будет получен стационарный ряд разностей, порядка d, изучают общий вид автокорреляционной и частной автокорреляционной функций этих разностей. Опираясь на теоретические свойства этих функций можно выбрать значения p и q для АР и СС операторов. Далее при выбранных p и q строятся начальные оценки параметров авторегрессии  и скользящего среднего b=(). Для авторегрессионных процессов используются уравнения Юла-Уокера, где теоретические автокорреляции заменены на их выборочные оценки. Для процессов скользящего среднего порядка q только первые q автокорреляций отличны от нуля и могут быть выражены через параметры  (см. ). Заменяя  их выборочными оценками  и решая получающиеся уравнения относительно , получим оценку . Эти предварительные оценки можно использовать как начальные значения для получения на следующих шагах более эффективных оценок.

Для смешанных процессов АРСС процедура оценивания усложняется . Так для рассмотренного в п. процесса АРСС(1,1) параметры и  , точнее их оценки, получаются из ( ) с заменой и  их выборочными оценками.

В общем случае вычисление начальных оценок процесса АРСС(p,q) представляет многостадийную процедуру и здесь не рассматривается. Отметим только, что для практики особый интерес имеют АР и СС процессы 1-го и 2-го порядков и простейший смешанный процесс АРСС(1,1).

В заключение заметим, что оценки автокорреляций, на основе которых строятся процедуры идентификации могут иметь большие дисперсии (особенно в условиях недостаточного объема выборки – несколько десятков наблюдений) и быть сильно коррелированны. Поэтому говорить о строгом соответствии теоретической и эмпирической автокорреляционных функций не приходится. Это приводит к затруднениям при выборе p, d, q, поэтому для дальнейшего исследования могут быть выбраны несколько моделей.

линейный ряд система временной ряд

Размещено на http://www.