Зв’язок розрахунку періодичного режиму із аналізом стійкості

4. Зв’язок розрахунку періодичного режиму із аналізом стійкості

 

Аналіз стійкості періодичного режиму нелінійної схемі повинен бути пов’язано з методом, за яким цей режим визначається. Інакше можна отримати результати, що не мають ніякого фізичного смислу. Для приклада звернемо увагу на частотну характеристику контуру із нелінійною ємністю. Дослідження стійкості, що виконане в відриві від методу розрахунку періодичного режиму, може привести до того, що точки із вертикальними дотичними не будуть визначати межі стійкості.

Так, як же повинні бути зв’язані ці дві задачі – розрахунок періодичного режиму та аналіз його стійкості? Щоб зрозуміти цей зв’язок скористаємось спектральним уявленням.

Припустимо, періодичний режим розраховується часовим методом. Тоді, на спектральний склад усталеного процесу обмеження не накладаються. Тому можна казати, що враховано багато гармонік (можливо нескінченна кількість). Цю обставину і треба мати на увазі при обранні методу дослідження стійкості: при аналізі повинно враховуватися багато гармонік. Очевидно підходять обидва розібрані вище методи, які опираються на характеристичну матрицю і нескінченний визначник Хіла.

Зараз припустимо, що періодичний режим був знайдений спектральним методом і було взято до уваги N гармонік. Нехай результати обліку ще однієї гармоніки практично співпали з попередніми. Це означає, що на лінійну частину схеми повинні бути накладені певні вимоги. Провідність  на частотах вище  повинна практично замикати затискачі, до яких ввімкнені нелінійні елементи. Якщо така вимога не виконується, то результати двох останніх розрахунків, про які мовилося вище, будуть відрізнятися один від одного. Таким чином, коли періодичний режим розраховано із врахуванням  гармонік і його результати припускаються достовірними, то модуль опору лінійної частини схеми на частотах, вище

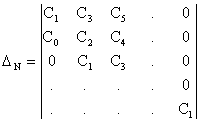
 ( - період розглядаємого режиму), дорівнює нулю або нескінченно великий. Цей факт і повинен лягти в основу обрання методу аналізу стійкості. Мабуть, в цьому випадку доцільно скористатися скінченим визначником Хіла, зберігаючи в ньому відповідне число рядків та стовпців.

стійкість рівновага періодичний режим

5. Аналіз стійкості періодичного режиму, отриманого часовим методом

 

Як вказувалося, в цій ситуації, щоб аналізувати стійкість, треба розраховувати характеристичну матрицю, або використовувати нескінченний визначник Хіла.

Шуканими даними для обчислення елементів характеристичної матриці є еквівалентна схема для малих збурень, в якій закон зміни параметрів кожного моделюючого елемента повинен бути задано, як функція часу. Подальша послідовність розрахунків така:

-  складання диференційного рівняння схеми для малих збурень;

-  n-кратне інтегрування цих рівнянь (n – порядок схеми) на протязі періоду модуляції при початкових умовах, заданих стовпцем одиничної матриці; це дозволяє сформувати характеристичну матрицю, так як після кожного інтегрування знаходимо значення змінних при , що дає один стовпець матриці;

-  розрахунок власних значень характеристичної матриці.

При другому методі використовується вираз, до якого приводиться нескінченний визначник. Якщо мати на увазі рівняння для малих збурень (9), то значення характеристичних показників потрібно знаходити за допомогою формули (12), прийнявши рівною нулю її праву частину.

Рішення рівняння, в якому невідоме входить як співмножник до аргументу тригонометричних функцій, надто складне. Позначивши , отримаємо

,

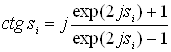причому .

В результаті

,

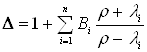де .

Після приведення до загального знаменника знайдемо

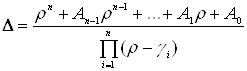. (14)

Поліном чисельника є характеристичним для рівняння (9), так його корені, зв’язані відповідним чином із характеристичними показниками, перетворюють в нуль визначник Хіла. Корені полінома знаменника є “мультиплікаторами” усередненої системи. Ступінь обох поліномів однакова. Коефіцієнти характеристичного полінома визначаються через “мультиплікатори” усередненої системи. Наприклад,

.

Формули для інших коефіцієнтів набагато складніші.

Таким чином, за допомогою нескінченного визначника Хіла маємо змогу знайти характеристичний поліном рівняння для малих збурень без інтегрування самого рівняння.

Аналіз стійкості із використанням нескінченного визначника Хіла можна зробити двома способами. Перший зводиться до обчислення коефіцієнтів характеристичного полінома. Другий заснований на вивченні годографа визначника при  та зміні частоти.

1. Опишемо перший алгоритм розглянутого методу. Шукані дані ті ж, що і в попередньому методі. Але для модульованих елементів повинні бути відомі коефіцієнти рядів Фур’є. Послідовність розрахунків виглядає так:

-  обчислення  - характеристичних коренів усередненої системи;

-  n-кратний розрахунок елементів чисельного визначника при  та розрахунок  за допомогою формули (13);

-  розрахунок коефіцієнтів характеристичного полінома;

-  обчислення характеристичних коренів або використання якого-небудь критерію стійкості.

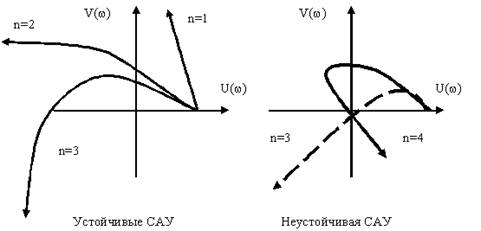
2. Перш ніж розглядати другий алгоритм, встановимо, яким умовам підпорядковано годограф визначника Хіла при стійкому та нестійкому періодичному режимі. Скористаємось формулою (14) і врахуємо такі обставини (рис. 1):

Рисунок 1 – До виводу критерію стійкості на основі годографа визначника Хіла

уявну вісь на площині характеристичних показників визначає вираз ;

перетворення  трансформує цю вісь в коло одиничного радіуса площини мультиплікаторів; при цьому ліві характеристичні показники переходять до внутрішніх точок кола одиничного радіуса, тобто в мультіплікатори з модулем, менше одиниці; коли дійсна частина характеристичного показника дорівнює нулю, а уявна змінюється в межах

. (15)

Кінець вектора  проходить проти часової стрілки все коло одиничного радіуса від точки ; при зміні  в великих межах кінець вектора  пройде по колу одиничного радіуса декілька разів.

Наше завдання – знайти кут повороту годографа  при зміні  в межах, визначених (15), та в умовах, коли всі мультиплікатори лежать усередині одиничного кола. Поворот годографа залежить ще від розташування мультиплікаторів усередненої системи, оскільки визначник Хіла є відношення двох характеристичних поліномів. Тому будемо вирішувати задачу при припущенні, що всі  знаходяться усередині одиничного кола. Нехай

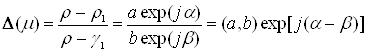
і ,  лежать усередині одиничного кола. Кінець вектора  рухається по одиничному колу. Поворот його на кут  змушує повернутися вектори  та  на кути  і , при цьому кут вектора  змінюється на величину, рівну різності . Коли вектор  зробить повний оберт, то  і кут повороту  буде дорівнювати нулю. Припустимо тепер, що мультиплікатор  розташовується зовні одиничного кола (рис.1, б), а  - як і раніше, усередині. Тоді видно, що  при . Результуючий кут повороту  стане рівним . Узагальнюючи на випадок відношення поліномів вільної ступені, може бути сформульован критерій стійкості періодичного режиму: якщо годограф нескінченного визначника Хіла при , зміні  в межах, заданих (15), та при лівих коренях усередненої системи не охоплює початок координат, то періодичний режим в нелінійної схемі стійкий; охват годографом початку координат свідчить про нестійкий періодичний режим.

2. Зараз можна описати другий алгоритм методу, спираючогося на нескінченний визначник Хіла. Шукані дані ті самі, що і для першого алгоритму, а послідовність розрахунка така:

-  вибір значення частоти;

-  розрахунок фази ;

-  складення с попередніми значеннями фази;

-  перехід до нового значення частоти та повтор розрахунку;

-  розрахунки завершуються при виході частоти за межі, обмежені нерівностями (15).

На вибір алгоритму із числа розглянутих впливає ряд факторів. Наприклад, ефективність програми чисельного інтегрування та програми обчислення визначника і т.і. Перший метод – чисельне інтегрування рівнянь для малих збурень з метою визначення елементів характеристичної матриці – зручний тим, що він використовує засоби, використані для розрахунку періодичного режиму. Однак остаточне рішення залежить від конкретних умов.

6. Аналіз стійкості періодичного режиму, розрахованого спектральним методом

В спектральному методі розрахунку періодичного режиму ураховується N гармонік, тому для аналізу використовується кінцевий визначник Хіла. Звичайно прийняти кількість рядків та стовпців в ньому рівним , тобто кількості рівнянь стаціонарного режиму.

Скінченний визначник Хіла втрачає періодичність по . В зв’язку з цим уявляється, що характеристичні показники уже немають властивості, яка виявлялось раніш: якщо  - корінь визначника, то коренями будуть і . Однак, скориставшись (11) та розкривши визначник, можна, після приведення до загального знаменника, отримати

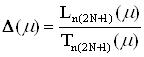, (16)

де L і T – поліноми від  степені n(2N+1), на що вказують нижні індекси,

n – порядок схеми.

Причому з процедури розкриття визначника і подальших перетворень можна знайти

.

Це указує на те, що у полінома знаменника корені проявляють ту саму властивість, як і полюси нескінченного визначника. Звідси витікає, що обговорювана властивість може мати місце і тоді, коли визначник неперіодичний. Мабуть, така властивість є і у характеристичних показників визначника, тобто у коренів полінома чисельника в (16). До жалю, цей факт поки не доведено. Якщо це вдалось би зробити, то з’явились можливость працювати над методом аналізу стійкості, спираючись на розрахунок характеристичних показників. Його алгоритм можна було подати в такому вигляді: розрахунок n близько розташованих коефіцієнтів полінома  та визначення по ним, на основі вказаної властивості коренів, коефіцієнтів полінома степені n. Наскільки важливо зниження степені полінома для характеристичних показників, видно з наступного прикладу. Нехай порядок системи рівнянь для схеми дорівнює 15, що ще припускає надійне обчислення коренів полінома. Якщо при розрахунку періодичного режиму враховані тільки три гармоніки, то прийдеться мати справу с поліномом ступеня .

Обміркуємо можливість використання алгоритмів, які відносилися до нескінченного визначника Хіла.

Розрахунок по формулі (14) тепер спрощується із-за скінченої розмірності визначника. Однак немає впевненості, що до (14) можна привести скінченний визначник. Недоведення цього факту народжує сумління в точності аналізу. Оскільки видно, що лише в границі, при , формула (14) точна.

Таким чином, аналіз стійкості періодичного режиму, при використанні скінченого визначника Хіла, утруднюється внаслідок не вирішення ряду питань.