Алгоритмы обработки данных линейной и нелинейной структуры

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Факультет автоматики и вычислительной техники

Информатика и вычислительная техника

Кафедра АИКС

АЛГОРИТМЫ ОБРАБОТКИ ДАННЫХ ЛИНЕЙНОЙ И НЕЛИНЕЙНОЙ СТРУКТУРЫ

Пояснительная записка к курсовому проекту

Студентка группы 8В84

А. C. Бушанова

Руководитель

Доцент каф. АИКС

И.В. Цапко

Томск – 2011г.

Задание на курсовое проектирование

Программно реализовать алгоритмы обработки данных, представленных в виде пирамиды (максимальной или минимальной – по выбору пользователя): преобразование массива в пирамиду, включение элемента в пирамиду, удаление элемента из пирамиды, вывод пирамиды на экран.

1.         Краткое словесное описание алгоритмов, используемых при решении поставленной задачи

Пирамида - законченное бинарное дерево, имеющее упорядочение узлов по уровням.

Различают максимальные пирамиды и минимальные.

В максимальной пирамиде родительский узел больше или равен каждому из своих сыновей. Корень содержит наибольший элемент.

В минимальной пирамиде родительский узел меньше или равен каждому из своих сыновей.

Корень содержит наименьший элемент.

На каждом уровне пирамида содержит 2ⁿ элементов, где n – номер уровня. Высота пирамиды , где N — количество элементов пирамиды.

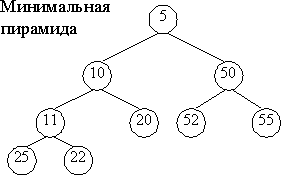
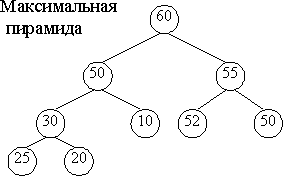
Пирамида используется в тех приложениях, где клиенту требуется прямой доступ к минимальному элементу.

Пирамида является списком, который хранит данные в виде бинарного дерева.

Все алгоритмы обработки пирамид сами должны обновлять дерево и поддерживать пирамидальное упорядочение.

Преобразование массива в пирамиду

Индекс последнего элемента пирамиды равен n-1.

Индекс его родителя равен (n-2)/2, и он определяет последний нелистовой узел пирамиды. Этот индекс является начальным для преобразования массива.

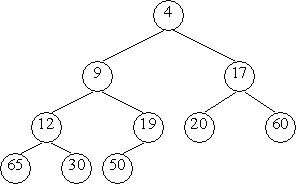
Рассмотрим целочисленный массив

int A[10] = {9, 12, 17, 30, 50, 20, 60, 65, 4, 19};

Индексы листьев: 5, 6, ..., 9.

Индексы родительских узлов: 4, 3, ..., 0.

Родитель А[4]=50, он больше своего сына А[9]=19 и поэтому должен поменяться с ним местами.

Родитель А[3]=30, он больше своего сына А[8]=4 и поэтому должен поменяться с ним местами (если меньших сына два, то меняется местами с наименьшим сыном).

На уровне 2 родитель А[2]=17 уже удовлетворяет условию пирамидальности, поэтому перестановок не производится.

Родитель А[1]=12 больше своего сына А[3]=4 и должен поменяться с ним местами.

Процесс прекращается в корневом узле. Родитель А[0]=9 должен поменяться местами со своим сыном А[1].

Результирующее дерево является пирамидой.

Включение элемента в пирамиду

1. Новый элемент добавляется в конец списка.

2. Если новый элемент имеет значение, меньшее, чем у его родителя, узлы меняются местами.

3. Новый родитель рассматривается как сын, и проверяется условие пирамидальности для более старшего родителя.

4. Процесс сканирует путь предков и завершается, встретив родителя, меньше чем новый элемент, или достигнув корневого узла.

Удаление из пирамиды

Данные удаляются всегда из корня дерева.

1. Удалить корневой узел и заменить его последним узлом.

2. Если новый корневой узел больше любого своего сына, то необходимо его поменять местами с наименьшим сыном.

3. Движение по пути меньших сыновей продолжается до тех пор, пока элемент не займет правильную позицию в качестве родителя или пока не будет достигнут конец списка.

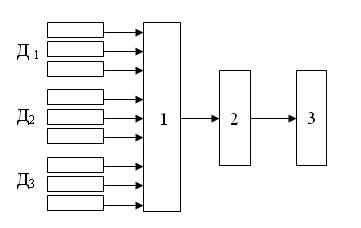
2.         Структурная схема программы с описанием

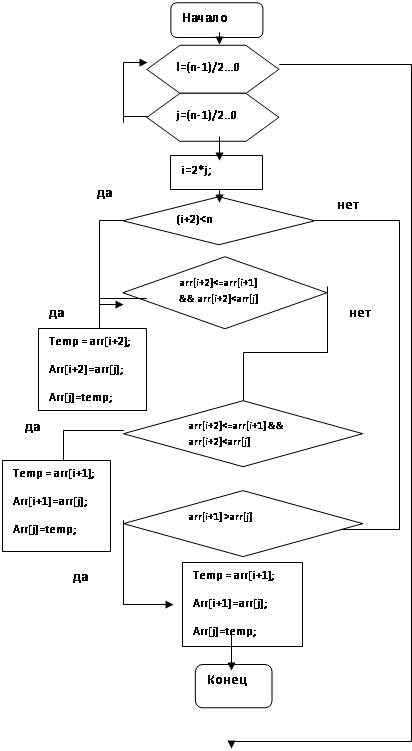
Схема взаимодействия функций программного комплекса:

		delElem(int t)

да

нет

да

makeArray()

ShowTree()

Heap_min()

Heap_max()

Структурные схемы алгоритмов:

Преобразование массива в максимальную пирамиду

Функция удаления элемента из пирамиды

нет

да

·      программы, нажмите на кнопку “Program’s Data”. Вверху под надписью “Array” будет выведен массив.

·       Если Вы желаете ввести данные самостоятельно, в поле над кнопками “Delete Element” и “Add Element”, введите число, затем нажмите кнопку “Add Element”, введенное число появится под надписью “Array”.

·      Далее следует выбрать тип пирамиды, для этого установите метку напротив желаемой пирамиды, затем нажмите кнопку “Show Tree”. В поле слева от панели параметров вы увидите получившуюся пирамиду.

·      Если Вы хотите добавить элемент в уже существующую пирамиду , в поле над кнопками “Delete Element” и “Add Element”, введите число, затем нажмите кнопку “Add Element”, введенное число будет добавлено в конец массива.

·      Если вы хотите удалить элемент, введите его значение в поле над кнопками “Delete Element” и “Add Element” и нажмите кнопку “Delete Element”, если этот элемент является корнем, произойдет его удаление.

пирамида максимальный минимальный алгоритм