Навигация
Пример выполнения программного комплекса
3. Пример выполнения программного комплекса
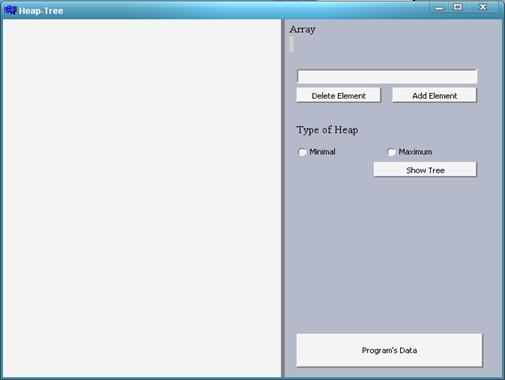
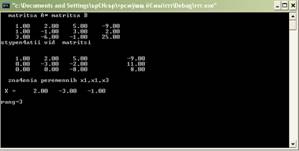
Рис. 1. Общий вид приложения
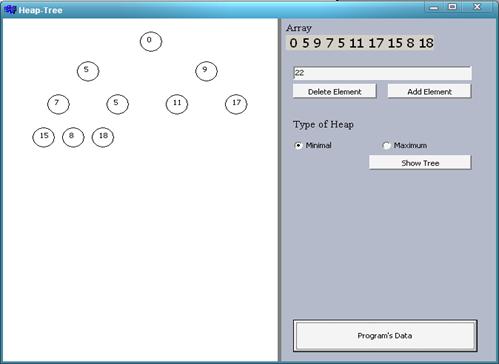
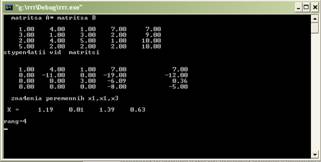
Рис. 2. Ввод данных и вывод пирамиды
Список используемой литературы
1. Цапко И.В. Структуры и алгоритмы обработки данных: учебное пособие Томск: Изд-во Томского политехнического университета, 2007. – 184 с.
Приложение А
Листинг программы
#include <vcl.h>
#pragma hdrstop
#include "UnitHeapTree.h"
#include <math.h>
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TFormHeapTree *FormHeapTree;
#define N 1000
//---------------------------------------------------------------------------
int array[N]; // используемый массив
int n=0; //фактическое количество элементов в массиве
//---------------------------------------------------------------------------
void makeArray() //создание массива, если пользователь
{ //предпочел использовать данные программы
randomize();
for(int i=0;i<10;i++)
array[i]=random(20);
n=10;
}
//-----------------функция преобразования массива в минимальную пирамиду -----------------
void heap_min()
{
int temp;
for(int l =floor((n-1)/2); l>=0; l--)
{
for(int j = floor((n-1)/2); j>=0; j--)
{
int i=2*j;
if((i+2)<n)
{
if(array[i+2]<=array[i+1] && array[i+2]<array[j])
{
temp = array[i+2];
array[i+2] = array[j];
array[j] = temp;
}
else
if(array[i+2]>=array[i+1] && array[i+1]<array[j])
{
temp = array[i+1];
array[i+1] = array[j];
array[j] = temp;
}
}
else
if(array[i+1]< array[j])
{
temp = array[i+1];
array[i+1] = array[j];
array[j] = temp;
}
}
}
}
//---------------функция преобразования массива в максимальную пирамиду -----------------
void heap_max()
{
int temp;
for(int l =floor((n-1)/2); l>=0; l--)
{
for(int j = floor((n-1)/2); j>=0; j--)
{
int i=2*j;
if((i+2)<n)
{
if(array[i+2]>=array[i+1] && array[i+2]>array[j])
{
temp = array[i+2];
array[i+2] = array[j];
array[j] = temp;
}
else
if(array[i+2]<=array[i+1] && array[i+1]>array[j])
{
temp = array[i+1];
array[i+1] = array[j];
array[j] = temp;
}
}
else
if(array[i+1]> array[j])
{
temp = array[i+1];
array[i+1] = array[j];
array[j] = temp;
}
}
}
}
//-------------------------удаление элемента из пирамиды ----------------------------------------
void delElem(int t)
{
int f;
for(int i=0; i<n; i++)
{
if(array[i]==t && i==0)
{
array[0]=array[n-1];
n=n-1;
break;
}
else
{
ShowMessage("This element is not a root or this element is not found");
break;
}
}
}
//-------------------функция очищения области рисования пирамиды -------------------------------
void Re(void)
{
FormHeapTree->ImageTree->Canvas->FillRect(Rect(0,0,FormHeapTree->ImageTree->Width,FormHeapTree->ImageTree->Height));
}
//-------------------------Функция вывода пирамиды на экран -------------------------------------------
void showTree()
{
Re();
int x = FormHeapTree->ImageTree->Width/2;
int y = 20;
int pr = 20;//расстояние между элементрами
if(n!=0)
{
int m = log(n)/log(2);
FormHeapTree->ImageTree->Canvas->Ellipse(x,20,x+30,50);
FormHeapTree->ImageTree->Canvas->TextOutA(x+10,y+5,array[0]);
//левое поддерово снизу вверх
for(int i=m; i>0; i--)
{
int q=pow(2,i-1)-1;
for(int j=pow(2,i)-1; j<=pow(2,i)+pow(2,i-1)-2; j++)
if(j<n)
{
FormHeapTree->ImageTree->Canvas->Ellipse(x-q*pr*2-pr-5, y+i*50-5, x-q*pr*2-pr+30-5, y+i*50-5+30);
FormHeapTree->ImageTree->Canvas->TextOutA(x-q*pr*2-pr+5, y+i*50, array[j]);
q--;
}
//правое поддерево
q=0;
for(int j = pow(2,i)+pow(2,i-1)-1; j<=pow(2,i+1)-2; j++)
if(j<n)
{
FormHeapTree->ImageTree->Canvas->Ellipse(x+q*pr*2+pr-5, y+i*50-5, x+q*pr*2+pr+30-5, y+i*50-5+30);
FormHeapTree->ImageTree->Canvas->TextOutA(x+q*pr*2+pr+5, y+i*50, array[j]);
q++;
}
pr*=2;
}
}
}
//---------------------------------------------------------------------------
__fastcall TFormHeapTree::TFormHeapTree(TComponent* Owner)
: TForm(Owner)
{
}
//---------------------------------функция вывода массива на экран ------------------------------------
void ShowArray()
{
FormHeapTree->LabelArray->Caption = "";
for(int i=0; i<n; i++)
FormHeapTree->LabelArray->Caption = FormHeapTree->LabelArray->Caption + " " + array[i];
}
//--------------------функция добавления элемента в пирамиду---------------------------------------
void __fastcall TFormHeapTree::SpeedButtonAddClick(TObject *Sender)
{
if(this->EditElem->Text != "")
{
try
{
int temp = StrToInt(this->EditElem->Text);
array[n] = temp;
this->LabelArray->Caption = this->LabelArray->Caption + " " + array[n];
n++;
}
catch(EConvertError &e)
{
ShowMessage("Please enter only numbers.");
}
}
else
ShowMessage("Please enter element!");
}
//----------------------функция непосредственно удаления элемента из пирамиды -----------
void __fastcall TFormHeapTree::SpeedButtonDeleteClick(TObject *Sender)
{
if(this->EditElem->Text != "")
{
try
{
int temp = StrToInt(this->EditElem->Text);
delElem(temp);
this->LabelArray->Caption = "";
ShowArray();
}
catch(EConvertError &e)
{
ShowMessage("Please enter only numbers.");
}
}
else
ShowMessage("Please enter element!");
}
//----------------- функция вывода пирамиды на экран ------------------------------------------------
void __fastcall TFormHeapTree::SpeedButtonShowTreeClick(TObject *Sender)
{
if(RadioButtonMin->Checked == true || RadioButtonMax->Checked == true)
{
if(RadioButtonMin->Checked)
{
// RadioButtonMax->Checked = false;
heap_min();
ShowArray();;
}
if(RadioButtonMax->Checked)
{
//RadioButtonMin->Checked = false;
heap_max();
ShowArray();
}
showTree();
}
else
ShowMessage("Please choose type of heap-tree.");
}
//------------ функция использоания данных программы-----------------------------------------------
void __fastcall TFormHeapTree::ButtonProgDataClick(TObject *Sender)
{
makeArray();
ShowArray();;
//---------------------------------------------------------------------------
Похожие работы
... дискретного программирование для решения задач проектирование систем обработки данных. - Сформулированы задачи диссертационного исследования. 2. БЛОЧНО-СИММЕТРИЧНЫЕ МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ В данном разделе рассматриваются общая постановка блочно-симметричной задачи дискретного программирования, её особенности и свойства. Разработан общий подход решения задач ...
... алгоритмов обработки информации СМСН с целью определения параметров движения ведущего ЛА и относительного движения. В этом случае нетрудно реализовать алгоритмы СМСН БЛА. Задачу обработки информации относительного движения рассматривали при полном составе измерений: углах визирования, угловой скорости линии визирования, дальности и скорости изменения дальности. Ключевым вопросом при решении этой ...
... , может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов. ...
... 4.Исходный текст программы Составить программу решения систем линейных алгебраических уравнений с квадратной невырожденной матрицей порядка n методом Гаусса с использованием языка С++ . // Решение системы линейных уравнений методом Гаусса. #include<io.h> #include "stdio.h" #include "conio.h" #include <windows.h> #include <iostream> #include <time.h> #include ...

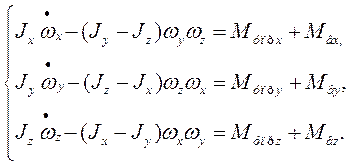
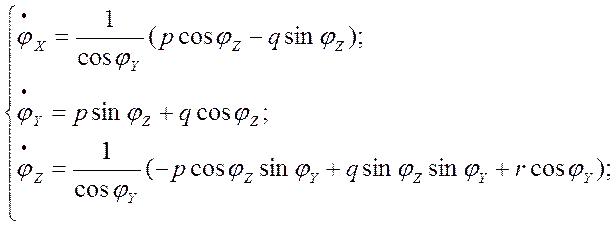
0 комментариев