Задание 1. Графическое решение задачи распределения ресурсов
· Записать стандартную и каноническую формы.
· Найти все базисные и допустимые базисные решения. Определить оптимальное базисное решение.
· Найти графически оптимальное базисное решение.
Фирма выпускает два вида изделий А и В. Каждое изделие проходит обработку на двух технологических линиях.
Известна таблица технологических коэффициентов ![]() - времени обработки (в минутах) каждого изделия на каждой технологической линии. Кроме этого, известны рыночная цена каждого изделия
- времени обработки (в минутах) каждого изделия на каждой технологической линии. Кроме этого, известны рыночная цена каждого изделия ![]() и
и ![]() и общее время каждой линии
и общее время каждой линии ![]() и
и ![]() .
.
| Изделия А | Изделия В | Общее время работы линии | |
| Линия 1 | 60 | 32 | 1920 |
| Линия 2 | 36 | 60 | 2160 |
| Цена одного изделия | 30 | 25 |
РЕШЕНИЕ
Запишем стандартную и каноническую формы
Обозначим:
![]() план выпуска изделия А;
план выпуска изделия А;
![]() план выпуска изделия В.
план выпуска изделия В.
Тогда затраты линии 1 и линии 2, необходимые для производства плана ![]() будут равны соответственно:
будут равны соответственно:
![]()
План ![]() будет допустимым, если затраты для линии 1 и линии 2 не превосходят общего времени работы каждой из линий, т.е. выполняются неравенства:
будет допустимым, если затраты для линии 1 и линии 2 не превосходят общего времени работы каждой из линий, т.е. выполняются неравенства:
![]()
Целевой функцией служит выручка от реализации допустимого плана ![]()
![]() при ограничениях
при ограничениях
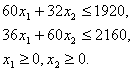 (1.1)
(1.1)
Для канонической формы эти ограничения нужно преобразовать в равенства. Для этого введём две дополнительные переменные
![]() остаток от производства на линии 1 (остаток времени обработки)
остаток от производства на линии 1 (остаток времени обработки)
![]() остаток от производства на линии 2 (остаток времени обработки).
остаток от производства на линии 2 (остаток времени обработки).
Тогда получим каноническую форму задачи:
-найти переменные ![]() , которые дают максимум целевой функции
, которые дают максимум целевой функции
![]() при ограничениях
при ограничениях
![]() (1.2)
(1.2)
· Найдём все базисные решения.
Полученные ограничения образуют систему двух уравнений с четырьмя неизвестными. Среди бесконечного множества решений этой системы базисные решения получаются следующим образом. Две переменных приравняем к 0. Эти переменные назовём свободными. Значения остальных переменных получаем из решения системы. Эти переменные назовём базисными. Базисное решение называется допустимым, если оно неотрицательно.
1) Пусть ![]() свободные переменные. Подставляя значения
свободные переменные. Подставляя значения ![]() (1.2), получаем систему уравнений
(1.2), получаем систему уравнений
![]()
Следовательно, базисное решение имеет вид
![]() .
.
Базисное решение означает, что изделия А и изделия В не производятся. Это базисное решение является допустимым. Выручка от реализации этого плана составит
![]() .
.
2) Пусть ![]() свободные переменные. Подставляя значения
свободные переменные. Подставляя значения ![]() (1.2) получаем систему
(1.2) получаем систему
![]()
Следовательно, базисное решение имеет вид
![]() .
.
Это базисное решение означает, что изделие А не производится, изделие В производится в количестве 60 ед., время изготовления продукции на линии 1 используется полностью, для производства на линии 2 не хватает 1440 минут работы. Это базисное решение не является допустимым.
3) Пусть ![]() свободные переменные. Подставляя значения
свободные переменные. Подставляя значения ![]() в (1.2) получаем систему
в (1.2) получаем систему
![]()
для базисных переменных ![]() и
и ![]() . Следовательно, базисное решение имеет вид
. Следовательно, базисное решение имеет вид
![]() .
.
Это базисное решение означает, что изделие А не производится, изделие В производится в количестве 36 единиц, время изготовления продукции линии 1 используется не полностью и его остаток составляет 768 минут, а на линии 2 используется полностью. Это базисное решение является допустимым. Выручка от реализации этого плана составит ![]() ден.ед.
ден.ед.
4) Пусть ![]() свободные переменные. Подставляя значения
свободные переменные. Подставляя значения ![]() в (1.2) получаем систему
в (1.2) получаем систему
![]()
для базисных переменных ![]() . Следовательно, базисное решение имеет вид
. Следовательно, базисное решение имеет вид ![]() . Базисное решение означает, что изделия А производится в количестве 32 ед., изделие В не производится, время изготовления продукции линии 1 используется полностью, а время изготовления линии 2 не полностью используется, его остаток составляет 1008 минут. Это базисное решение является допустимым. Выручка от реализации этого плана составит
. Базисное решение означает, что изделия А производится в количестве 32 ед., изделие В не производится, время изготовления продукции линии 1 используется полностью, а время изготовления линии 2 не полностью используется, его остаток составляет 1008 минут. Это базисное решение является допустимым. Выручка от реализации этого плана составит
![]() ден. ед.
ден. ед.
5) Пусть ![]() свободные переменные. Подставляя значения
свободные переменные. Подставляя значения ![]() в (1.2) получаем систему
в (1.2) получаем систему
![]()
для базисных переменных ![]() . Следовательно, базисное решение имеет вид
. Следовательно, базисное решение имеет вид ![]() . Это базисное решение означает, что изделия А производится 60 ед., изделие В не производится, не хватает времени обработки 1680 минут для первой линии, а время обработки второй линии используется полностью. Это базисное решение не является допустимым.
. Это базисное решение означает, что изделия А производится 60 ед., изделие В не производится, не хватает времени обработки 1680 минут для первой линии, а время обработки второй линии используется полностью. Это базисное решение не является допустимым.
6) Пусть ![]() свободные переменные. Тогда базисные переменные
свободные переменные. Тогда базисные переменные ![]() и
и ![]() найдём из системы уравнений
найдём из системы уравнений
![]()
Отсюда следует, что базисное решение имеет вид ![]() . Это решение означает, что изделия А производятся в количестве
. Это решение означает, что изделия А производятся в количестве ![]() ед., изделия В производятся в количестве
ед., изделия В производятся в количестве ![]() , время обработки на каждой из линий используется полностью. Это базисное решение является допустимым. Выручка от реализации составит
, время обработки на каждой из линий используется полностью. Это базисное решение является допустимым. Выручка от реализации составит ![]() ден.ед.
ден.ед.
· Определим оптимальное базисное решение.
Из теории линейного программирования следует, что оптимальное решение можно найти среди допустимых базисных решений. Отсюда следует, что для определения оптимального решения нужно вычислить значения целевой функции на всех допустимых базисных решениях. Оптимальным будет базисное решение, на котором значение целевой функции наибольшее.
В таблице 1.1 приведены все допустимые базисные решения и соответствующие им значения выручки ![]() .
.
двойственный задача равновесный спрос полезность товар
Таблица 1.1
| № | Базисные переменные | Небазисные переменные |
| ||
| 1 |
|
|
|
|
|
| 2 |
|
|
|
|
|
| 3 |
|
|
|
|
|
| 4 |
|
|
|
|
|
Максимальное значение выручки достигается на четвёртом базисном решении в этой таблице
![]()
Следовательно, изделие А производится в количестве ![]() ед., изделие В производится в количестве
ед., изделие В производится в количестве ![]() ед., время обработки на каждой из линий используется полностью (
ед., время обработки на каждой из линий используется полностью (![]() ).
).
Графическое решение задачи
Рассмотрим задачу в стандартной форме: найти переменные ![]() , которые обеспечивают максимальное значение функции
, которые обеспечивают максимальное значение функции ![]()
![]()
при ограничениях
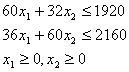
На горизонтальной оси прямоугольной системы координат будем откладывать план выпуска продукции ![]() , а на вертикальной – план выпуска второй продукции
, а на вертикальной – план выпуска второй продукции ![]() .
.
Рассмотрим первое ограничение ![]() . Множество точек, удовлетворяющих равенству
. Множество точек, удовлетворяющих равенству ![]() , образует прямую на плоскости. Построим эту прямую по её точкам пересечения с осями координат. Для определения координат точки А пересечения с осью
, образует прямую на плоскости. Построим эту прямую по её точкам пересечения с осями координат. Для определения координат точки А пересечения с осью ![]() в уравнение подставим
в уравнение подставим ![]() . Из него следует
. Из него следует ![]() , т.е
, т.е ![]() . Для определения координат точки В пересечения с осью
. Для определения координат точки В пересечения с осью ![]() в уравнение подставим
в уравнение подставим ![]() . Из него следует
. Из него следует ![]() , т.е.
, т.е. ![]() . Неравенству
. Неравенству ![]() удовлетворяют все точки одной из полуплоскостей, которые образовала построенная прямая. Для её определения достаточно проверить справедливость неравенства для одной точки. Для начала координат
удовлетворяют все точки одной из полуплоскостей, которые образовала построенная прямая. Для её определения достаточно проверить справедливость неравенства для одной точки. Для начала координат ![]() неравенство выполняется. Следовательно, все точки полуплоскости, содержащей начало координат, будут графическим изображением этого неравенства. Аналогично построим прямую
неравенство выполняется. Следовательно, все точки полуплоскости, содержащей начало координат, будут графическим изображением этого неравенства. Аналогично построим прямую ![]() по её точкам пересечения с осями координат:
по её точкам пересечения с осями координат: ![]() . Все точки полуплоскости, содержащей начало координат
. Все точки полуплоскости, содержащей начало координат ![]() будут графическим изображением неравенства
будут графическим изображением неравенства ![]() . Учитывая ограничения на знак
. Учитывая ограничения на знак ![]() , множество точек четырёхугольника
, множество точек четырёхугольника ![]() является множеством всех допустимых решений. Все угловые точки (крайние точки) четырёхугольника
является множеством всех допустимых решений. Все угловые точки (крайние точки) четырёхугольника ![]() соответствуют допустимым базисным решениям:
соответствуют допустимым базисным решениям:
угловая точка ![]() соответствует базисному решению
соответствует базисному решению
![]() ,
, ![]() ,
, ![]() ;
;
угловая точка ![]() соответствует базисному решению
соответствует базисному решению
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
угловая точка ![]() соответствует базисному решению
соответствует базисному решению
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
угловая точка ![]() соответствует базисному решению
соответствует базисному решению ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
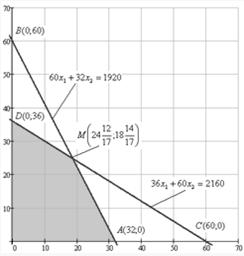
Теперь графически найдём точку четырёхугольника ![]() , которая определит оптимальное решение.
, которая определит оптимальное решение.
Из теорем математического анализа следует, что оптимальное решение следует искать только среди точек границы четырёхугольника ![]() . Для её определения в начале координат построим вектор
. Для её определения в начале координат построим вектор ![]() , координаты которого являются рыночными ценами. Прямая
, координаты которого являются рыночными ценами. Прямая ![]() проходит через начало координат перпендикулярно вектору
проходит через начало координат перпендикулярно вектору ![]() . Она определяет все планы, в которых выручка равна 0. Вектор
. Она определяет все планы, в которых выручка равна 0. Вектор ![]() указывает направление возрастания выручки. Если прямую нулевой выручки (розовая линия) перемещать параллельно в направлении вектора
указывает направление возрастания выручки. Если прямую нулевой выручки (розовая линия) перемещать параллельно в направлении вектора ![]() , то значение выручки будет увеличиваться. Так как среди внутренних точек четырёхугольника
, то значение выручки будет увеличиваться. Так как среди внутренних точек четырёхугольника ![]() оптимального решения не может быть, то прямую нужно переместить до границы четырёхугольника
оптимального решения не может быть, то прямую нужно переместить до границы четырёхугольника ![]() , т.е. до точки
, т.е. до точки ![]() .
.
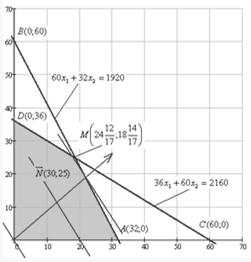
Таким образом, точка ![]() определяет оптимальное решение. Соответствующее точке
определяет оптимальное решение. Соответствующее точке ![]() базисное решение
базисное решение
![]()
является оптимальным решением. Максимальная выручка будет равна ![]() . Уравнение
. Уравнение ![]() определяет уравнение максимальной выручки (верхняя розовая линия).
определяет уравнение максимальной выручки (верхняя розовая линия).
Задание 2. Двойственная задача
· Записать двойственную задачу и дать её экономический смысл.
· Найти оптимальное решение двойственной задачи.
· Определить целесообразность производства продукции С, для которой на изготовление единицы продукции требуется 60 минут и 50 минут времени изготовления на первой и второй линии соответственно. Рыночная цена составляет 120 ден. ед. за единицу продукции.
РЕШЕНИЕ
Запишем двойственную задачу и дадим её экономический смысл.
Правило построения двойственной задачи состоит в следующем. Каждому равенству прямой задачи соответствует двойственная переменная
![]()
Стрелки показывают, что первому равенству соответствует переменная ![]() , а второму – переменная
, а второму – переменная ![]() .
.
Для определения целевой функции ![]() двойственной задачи двойственные переменные
двойственной задачи двойственные переменные ![]() и
и ![]() умножаются на правые части равенств и складываются:
умножаются на правые части равенств и складываются:
![]() .
.
Каждой переменной прямой задачи ![]() соответствует ограничение двойственной задачи. Левые части этих ограничений для переменной
соответствует ограничение двойственной задачи. Левые части этих ограничений для переменной ![]() записываются следующим образом. Двойственные переменные
записываются следующим образом. Двойственные переменные ![]() и
и ![]() умножаются на коэффициенты перед переменной
умножаются на коэффициенты перед переменной ![]() и складываются:
и складываются: ![]() .
.
Аналогично, записываются левые части ограничений для переменной ![]() . Двойственные переменные
. Двойственные переменные ![]() и
и ![]() умножаются на коэффициенты перед переменной
умножаются на коэффициенты перед переменной ![]() и складываются:
и складываются: ![]() . Левая часть ограничений для переменной
. Левая часть ограничений для переменной ![]() равна
равна ![]() , а для переменной
, а для переменной ![]() . Правые части ограничений равны коэффициентам 30, 25, 0, 0 целевой функции
. Правые части ограничений равны коэффициентам 30, 25, 0, 0 целевой функции ![]()
![]()
перед переменными ![]() . Левые и правые части ограничений соединяются знаком
. Левые и правые части ограничений соединяются знаком ![]() .
.
В результате двойственная задача имеет вид:
найти двойственные переменные ![]() и
и ![]() , при которых целевая функция
, при которых целевая функция ![]() минимальна
минимальна
![]()
при ограничениях
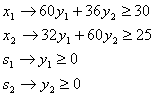
Переменные ![]() , называются допустимым решением двойственной задачи, если они удовлетворяют всем ограничениям и оптимальными, если они допустимые и на них целевая функция
, называются допустимым решением двойственной задачи, если они удовлетворяют всем ограничениям и оптимальными, если они допустимые и на них целевая функция ![]() достигает минимума.
достигает минимума.
Экономический смысл двойственной задачи:
двойственная переменная ![]() определяет теневую цену работы 1 минуты оборудования линии 1, а двойственная переменная
определяет теневую цену работы 1 минуты оборудования линии 1, а двойственная переменная ![]() определяет теневую цену работы 1 минуты оборудования линии 2.
определяет теневую цену работы 1 минуты оборудования линии 2.
Тогда целевая функция ![]() задаёт стоимость времени работы оборудования в теневых ценах соответственно для линии 1 и линии 2.
задаёт стоимость времени работы оборудования в теневых ценах соответственно для линии 1 и линии 2.
Выражение ![]() определяет стоимость 60 минут и 36 минут, затраченных на изготовление единицы изделия А в теневых ценах, а выражение
определяет стоимость 60 минут и 36 минут, затраченных на изготовление единицы изделия А в теневых ценах, а выражение ![]() определяет стоимость 32 минут и 60 минут, затраченных на изготовление единицы изделия В в теневых ценах.
определяет стоимость 32 минут и 60 минут, затраченных на изготовление единицы изделия В в теневых ценах.
Определим величины приведённых стоимостей.
![]()
Если величина ![]() положительна, то стоимость ресурсов больше рыночной цены этого продукта. В этом случае производство продукта убыточно. Если величина
положительна, то стоимость ресурсов больше рыночной цены этого продукта. В этом случае производство продукта убыточно. Если величина ![]() отрицательна, то стоимость ресурсов меньше рыночной цены этого продукта. Если величина
отрицательна, то стоимость ресурсов меньше рыночной цены этого продукта. Если величина ![]() равна 0, то стоимость ресурсов равна рыночной цене. Ограничения двойственной задачи
равна 0, то стоимость ресурсов равна рыночной цене. Ограничения двойственной задачи
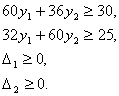
Отсюда следует, что при допустимых теневых ценах ![]() производство обоих продуктов неприбыльно.
производство обоих продуктов неприбыльно.
Можно дать следующую экономическую интерпретацию двойственной задачи. Некоторая фирма предлагает производителю продукции продать ей все запасы ресурсов по теневым ценам ![]() и
и ![]() . Решение двойственной задачи определяет минимальный уровень рыночных цен
. Решение двойственной задачи определяет минимальный уровень рыночных цен ![]() , при котором производить продукцию неприбыльно.
, при котором производить продукцию неприбыльно.
Найдём оптимальное решение двойственной задачи
Из первого задания следует, что допустимое базисное решение
![]()
является оптимальным решением прямой задачи.
По оптимальному базисному решению ![]() прямой задачи найдём оптимальное решение двойственной. Для этого все ограничения двойственной задачи, соответствующие базисным переменным
прямой задачи найдём оптимальное решение двойственной. Для этого все ограничения двойственной задачи, соответствующие базисным переменным ![]() нужно заменить равенствами
нужно заменить равенствами
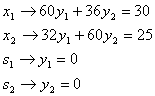
Из этих равенств найдём оптимальные значения двойственных переменных ![]() , минимальное значение целевой функции равно
, минимальное значение целевой функции равно
![]() .
.
Оптимальная теневая цена работы 1 минуты оборудования линии 1 равна ![]() , а оптимальная теневая цена 1 минуты оборудования линии 2 равна
, а оптимальная теневая цена 1 минуты оборудования линии 2 равна ![]() .
.
Стоимость работы технологического оборудования, затраченных на изготовление единицы изделия А равна
![]() ,
,
а стоимость работы технологического оборудования, затраченных на изготовление единицы изделия В равна
![]() .
.
Приведённые стоимости каждого вида изделия будут раны
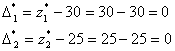
Отсюда следует, что производство изделий А и В рентабельно.
Определим целесообразность производства продукции С, для которой на изготовление единицы продукции требуется 60 минут и 50 минут времени изготовления на первой и второй линии соответственно. Рыночная цена составляет 120 ден. ед. за единицу продукции. Для этого вычислим стоимость ресурсов, затраченных на изготовление единицы продукции С:
![]() ден. ед.
ден. ед.
Приведённая стоимость этого вида продукции будет равна
![]() .
.
Отсюда следует, что производство единицы продукции С принесёт прибыль ![]() ден. ед.
ден. ед.
Задание 3. Функция полезности
Пусть функция полезности наборов из двух товаров ![]() имеет вид
имеет вид ![]() , где
, где
![]() .
.
· Найти набор товаров, который имеет такую же полезность, как набор ![]() и количество второго товара равно 1.
и количество второго товара равно 1.
· Для набора ![]() найти предельные полезности первого и второго товаров.
найти предельные полезности первого и второго товаров.
· В наборе ![]() количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.
количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.
РЕШЕНИЕ
1. Функция полезности имеет вид: ![]() . Найдём полезность набор
. Найдём полезность набор ![]() :
:
![]()
Кривая безразличия ![]() определяет все наборы товаров, которые имеют такую же полезность как набор
определяет все наборы товаров, которые имеют такую же полезность как набор ![]() . Из этого уравнения можно найти набор товаров, в котором количества второго товара равно
. Из этого уравнения можно найти набор товаров, в котором количества второго товара равно ![]() , подставив это значение в уравнение кривой безразличия
, подставив это значение в уравнение кривой безразличия ![]() ,
, ![]() . Таким образом, наборы
. Таким образом, наборы ![]() и
и ![]() безразличны для потребителя.
безразличны для потребителя.
2. Найдём частные производные функции полезности ![]()
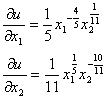
Предельная полезность первого товара в наборе ![]() равна значению частной производной
равна значению частной производной ![]() в точке (3,8):
в точке (3,8):
![]() .
.
Предельная полезность второго товара в наборе ![]() равна значению частной производной
равна значению частной производной ![]() в точке (3,8):
в точке (3,8):
![]()
Найдём изменение полезности, если количество первого товара увеличивается на 0,1, т.е. ![]() , а количество второго товара уменьшается на 0,2, т.е.
, а количество второго товара уменьшается на 0,2, т.е. ![]() . Приближённое изменение полезности вычислим по формуле
. Приближённое изменение полезности вычислим по формуле
![]() .
.
Следовательно, полезность набора ![]() , равная
, равная ![]() , увеличивается на 0,0065. Таким образом, полезность нового набора
, увеличивается на 0,0065. Таким образом, полезность нового набора ![]()
Задание 4. Модель Стоуна
Функция полезности потребителя имеет вид
![]() , где
, где
![]() .
.
1. Найти равновесный спрос и его полезность, если рыночная цена первого товара ![]() , рыночная цена второго товара
, рыночная цена второго товара ![]() и потребитель выделяет на приобретение товаров сумму
и потребитель выделяет на приобретение товаров сумму ![]() денежных единиц.
денежных единиц.
2. Найти функции спроса на оба вида товаров.
3. Найти спрос на оба товара при увеличении дохода на 30 денежных единиц и при уменьшении дохода на 60 денежных единиц.
РЕШЕНИЕ
1. Функция полезности потребителя имеет вид
![]() .
.
Вычислим равновесный спрос при заданных ценах и доходе. Найдём стоимость минимального набора товаров
![]() .
.
Оставшаяся сумма денег ![]() распределяется пропорционально коэффициентам эластичности этих товаров
распределяется пропорционально коэффициентам эластичности этих товаров
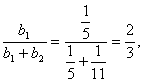
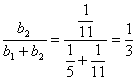 .
.
На приобретение первого товара выделяется сумма
![]() .
.
На приобретение 2-го товара - сумма
![]() .
.
Поделив выделенные средства на рыночные цены товаров, получаем количество товара, приобретаемое сверх установленных нормативов
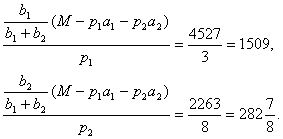
Таким образом, оптимальный спрос составит
![]() единиц первого товара и
единиц первого товара и
![]() единиц второго товара.
единиц второго товара.
Полезность равновесного набора будет равна
![]() .
.
2. Найдём функции спроса, заменяя в формулах спроса
![]() ,
, ![]()
![]() .
.

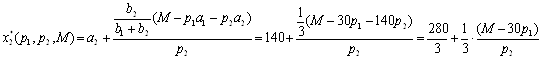
Эти формулы определяют спрос на продукцию при любых ценах и доходах.
3. Оценим влияние на спрос изменения дохода обоих товаров. Найдём реакцию спроса на изменение дохода на 1 денежную единицу. Частные производные по доходу 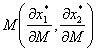 показывают изменение спроса на первый и второй товары соответственно при возрастании дохода на 1 денежную единицу.
показывают изменение спроса на первый и второй товары соответственно при возрастании дохода на 1 денежную единицу.
Дифференцируя полученные выше функции спроса по М, получаем
![]()
![]() .
.
Вычислим эти частные производные при заданных ![]() и
и ![]() :
:
![]()
![]()
![]() .
.
Так как значения частных производных положительные, то оба товара являются ценными: с ростом дохода на 1 денежную единицу спрос на оба товара растёт: спрос на первый товар увеличивается на ![]() , а второго - на
, а второго - на ![]() .
.
При увеличении дохода потребителя на 30 денежных единиц спрос на первый товар увеличится на ![]() единицы, а второго на
единицы, а второго на ![]() и составит
и составит
![]() ,
, ![]() .
.
При уменьшении дохода потребителя на 60 денежных единиц спрос на первый товар снизится на ![]() единиц, а спрос на второй товар снизится на
единиц, а спрос на второй товар снизится на ![]() единиц и составит соответственно:
единиц и составит соответственно:
![]() ,
, ![]() .
.
Похожие работы
... переменных, доставляющих экстремум линейной целевой функции при m ограничениях в виде линейных равенств или неравенств. Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи: · рационального использования сырья и материалов; задачи оптимизации раскроя; · оптимизации производственной программы ...
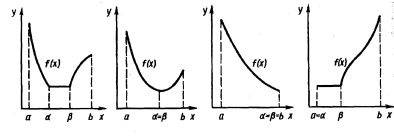
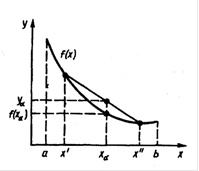
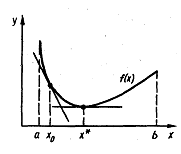
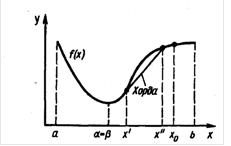
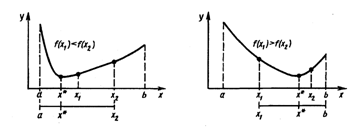
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
... ”, 1982. 3. Организация обслуживания при ограниченной информации о надёжности системы / Е. Ю. Бразилович, В. А. Каштанов – Москва, “Советское радио”, 1975. 4. Некоторые математические вопросы теории обслуживания сложных систем / Е. Ю. Бразилович, В. А. Каштанов, Москва, “Радио и связь”, 1971. 5. Теория систем / В. А. Острековский – Москва, “Высшая ...
... моделей экстремальных планов и экстремальных значений целевой функции быть не может. Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение. Методика построения экономико-математической модели состоит в том, чтобы ...


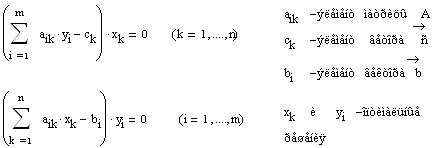
0 комментариев