Навигация
Линейное программирование как метод оптимизации
Содержание
Введение
1. Общая постановка задачи линейного программирования (ЛП)
2. Приведение задачи линейного программирования к стандартной форме
3. Примеры экономических задач, приводящихся к задачам ЛП
4. Геометрический метод решение задач ЛП
5. Симплексный метод решения задач ЛП
6. Теоремы двойственности и их использование в задачах ЛП
6. Транспортная задача и её решение методом потенциалов
Заключение
Литература
Введение
В настоящее время оптимизация находит применение в науке, технике и в любой другой области человеческой деятельности.
Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др.). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно.
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
· количество продукции - расход сырья
· количество продукции - качество продукции
Выбор компромиcсного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого. Приведем примеры.
Типичный пример неправильной постановки задачи оптимизации:
"Получить максимальную производительность при минимальной себестоимости".
Ошибка заключается в том, что ставится задача поиска оптимальности 2-х величин, противоречащих друг другу по своей сути.
Правильная постановка задачи могла быть следующая:
а) получить максимальную производительность при заданной себестоимости;
б) получить минимальную себестоимость при заданной производительности;
В первом случае критерий оптимизации - производительность, а во втором - себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта.
3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учет ограничений.
Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта (аппарат, цех, завод). Оптимизируемый вариант работы объекта должен оцениваться какой-то количественной мерой - критерием оптимальности.
Критерием оптимальности называется количественная оценка оптимизируемого качества объекта.
На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации.
Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.
В зависимости от своей постановки, любая из задач оптимизации может решаться различными методами, и наоборот - любой метод может применяться для решения многих задач. Методы оптимизации могут быть скалярными (оптимизация проводится по одному критерию), векторными (оптимизация проводится по многим критериям), поисковыми (включают методы регулярного и методы случайного поиска), аналитическими (методы дифференциального исчисления, методы вариационного исчисления и др.), вычислительными (основаны на математическом программировании, которое может быть линейным, нелинейным, дискретным, динамическим, стохастическим, эвристическим и т.д.), теоретико-вероятностными, теоретико-игровыми и др. Подвергаться оптимизации могут задачи как с ограничениями, так и без них.
Линейное программирование - один из первых и наиболее подробно изученных разделов математического программирования. Именно линейное программирование явилось тем разделом, с которого начала развиваться сама дисциплина "математическое программирование". Термин "программирование" в названии дисциплины ничего общего с термином "программирование (т.е. составление программ) для ЭВМ" не имеет, так как дисциплина "линейное программирование" возникла еще до того времени, когда ЭВМ стали широко применяться при решении математических, инженерных, экономических и др. задач. Термин "линейное программирование" возник в результате неточного перевода английского "linear programming". Одно из значений слова "programming" - составление планов, планирование. Следовательно, правильным переводом "linear programming" было бы не "линейное программирование", а "линейное планирование", что более точно отражает содержание дисциплины. Однако, термин линейное программирование, нелинейное программирование и т.д. в нашей литературе стали общепринятыми.
Итак, линейное программирование возникло после Второй Мировой Войны и стал быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а так же математической "стройности".
Можно сказать, что линейное программирование применимо для построения математических моделей тех процессов, в основу которых может быть положена гипотеза линейного представления реального мира: экономических задач, задач управления и планирования, оптимального размещения оборудования и пр.
Задачами линейного программирования называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и неравенств. Кратко задачу линейного программирования можно сформулировать следующим образом: найти вектор значений переменных, доставляющих экстремум линейной целевой функции при m ограничениях в виде линейных равенств или неравенств.
Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи:
· рационального использования сырья и материалов; задачи оптимизации раскроя;
· оптимизации производственной программы предприятий;
· оптимального размещения и концентрации производства;
· составления оптимального плана перевозок, работы транспорта;
· управления производственными запасами;
· и многие другие, принадлежащие сфере оптимального планирования.
Так, по оценкам американских экспертов, около 75% от общего числа применяемых оптимизационных методов приходится на линейное программирование. Около четверти машинного времени, затраченного в последние годы на проведение научных исследований, было отведено решению задач линейного программирования и их многочисленных модификаций.
Первые постановки задач линейного программирования были сформулированы известным советским математиком Л.В. Канторовичем, которому за эти работы была присуждена Нобелевская премия по экономике.
Значительное развитие теория и алгоритмический аппарат линейного программирования получили с изобретением и распространением ЭВМ и формулировкой американским математиком Дж. Дансингом симплекс-метода.
В развитие и совершенствование этих систем вложен труд и талант многих математиков, аккумулирован опыт решения тысяч задач. Владение аппаратом линейного программирования необходимо каждому специалисту в области математического программирования. Линейное программирование тесно связано с другими методами математического программирования (например, нелинейного программирования, где целевая функция нелинейная).
Задачи с нелинейной целевой функцией и линейными ограничениями называют задачами нелинейного программирования с линейными ограничениями. Оптимизационные задачи такого рода можно классифицировать на основе структурных особенностей нелинейных целевых функций. Если целевая функция Е - квадратичная функция, то мы имеем дело с задачей квадратичного программирования; если Е - это отношение линейных функций, то соответствующая задача носит название задачи дробно-линейного программирования, и т.д. Деление оптимизационных задач на эти классы представляет значительный интерес, поскольку специфические особенности тех или иных задач играют важную роль при разработке методов их решения.
1. Общая постановка задачи линейного программирования (ЛП)
Задача линейного программирования (ЛП) состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях.
Общая форма задачи имеет вид: найти ![]() при условиях
при условиях
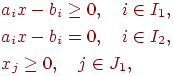
Где
![]()
Здесь и далее нам удобнее считать с и аі вектор - строками, а x и b= (b1,...,bm) T - вектор столбцами.
Наряду с общей формой широко используются также каноническая и стандартная формы. Как в канонической, так и в стандартной форме
![]()
т.е. все переменные в любом допустимом решении задачи должны принимать неотрицательные значения (такие переменные принято называть неотрицательные в отличие от так называемых свободных переменных, на область значений которых подобное ограничение не накладывается). Отличие же между этими формами состоит в том, что в одном случае I2 = 0, а в другом - I1 = 0.
Задача ЛП в канонической форме:
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
![]() (2.3)
(2.3)
Задача ЛП в стандартной форме:
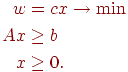
В обоих случаях А есть матрица размерности m x n, i-я строка которой совпадает с вектором аi.
Задача ЛП в общей форме сводится (в определенном смысле) к задаче ЛП в канонической (стандартной) форме. Под этим понимается существование общего способа построения по исходной задаче (в общей форме) новой задачи ЛП (в нужной нам форме), любое оптимальное решение которой "легко" преобразуется в оптимальное решение исходной задачи и наоборот. (Фактически, связь между этими задачами оказывается еще более тесной). Тем самым мы получаем возможность, не теряя общности, заниматься изучением задач ЛП, представленных либо в канонической, либо в стандартной форме. Ввиду этого наши дальнейшие рассмотрения задач ЛП будут посвящены, главным образом, задачам в канонической форме.
2. Приведение задачи линейного программирования к стандартной форме
Любая задача линейного программирования приводится к стандартной (канонической) форме основной задачи линейного программирования, которая формулируется следующим образом: найти неотрицательные значения переменных X1, X2, Xn, удовлетворяющих ограничениям в виде равенств:
A11X1 + A12X2 + … + A1nXn = B1;
A21X1 + A22X2 + … + A2nXn = B2;
……………………………………
Am1X1 + Am2X2 + … + AmnXn = Bm;
Xj ≥ 0, j=1,…,n
и обращающих в максимум линейную функцию этих переменных:
E = C1X1 + C2X2 + … + CnXn Þ max
При этом также требуется, чтобы правые части равенств были неотрицательны, т.е. должны соблюдаться условия:
Bj ≥ 0, j=1,…,n
Приведение к стандартной форме необходимо, так как большинство методов решения задач линейного программирования разработано именно для стандартной формы. Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия:
перейти от минимизации целевой функции к ее максимизации;
изменить знаки правых частей ограничений;
перейти от ограничений-неравенств к равенствам;
избавиться от переменных, не имеющих ограничений на знак.
Для решения нашей задачи воспользуемся симплекс-методом, так как этот метод предназначен для решения задач линейного программирования любой размерности.
3. Примеры экономических задач, приводящихся к задачам ЛП
Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи и прочие.
Рассмотрим некоторые из них.
Определение оптимального ассортимента. Имеются m видов ресурсов в количествах b1, b2,., bi, bm и n видов изделий. Задана матрица A=||aij||, i=1,.,m, j=1,.,n, где aij характеризует нормы расхода i-го ресурса на единицу j-го вида изделий. Эффективность производства j-го вида изделий характеризуется показателем Cj, удовлетворяющим условию линейности. Нужно определить такой план выпуска изделий (оптимальный ассортимент), при котором суммарный показатель эффективности будет наибольший.
Обозначим количество единиц k-го вида изделий, выпускаемых предприятием, через xk, ![]() . Тогда математическая модель этой задачи будет иметь такой вид:
. Тогда математическая модель этой задачи будет иметь такой вид:
![]() (3.1)
(3.1)
при ограничениях
![]() (3.2)
(3.2)
Кроме ограничений на ресурсы (3.2) в эту модель можно ввести дополнительные ограничения на планируемый уровень выпуска продукции ![]() , xi: xj: xk = bi: bj: bk для всех i, j, k и т.д.
, xi: xj: xk = bi: bj: bk для всех i, j, k и т.д.
Оптимальное распределение взаимозаменяемых ресурсов. Имеются m видов взаимозаменяемых ресурсов а1, а2,., аm, используемых при выполнении n различных работ (задач). Объемы работ, которые должны быть выполнены, составляют b1, b2,., bi, bn единиц. Заданы числа ![]() , указывающие, сколько единиц j-й работы можно получить из единицы і-го ресурса, а также Cij - затраты на производство j-й работы из единицы i-го ресурса. Требуется распределить ресурсы по работам таким образом, чтобы суммарная эффективность выполненных работ была максимальной (или суммарные затраты - минимальными).
, указывающие, сколько единиц j-й работы можно получить из единицы і-го ресурса, а также Cij - затраты на производство j-й работы из единицы i-го ресурса. Требуется распределить ресурсы по работам таким образом, чтобы суммарная эффективность выполненных работ была максимальной (или суммарные затраты - минимальными).
Данная задача называется общей распределительной задачей. Количество единиц i-го ресурса, которое выделено на выполнение работ j-го вида, обозначим через xij.
Математическая модель рассматриваемой задачи такова:
![]() (3.3)
(3.3)
при ограничениях
![]() (3.4)
(3.4)
![]() (3.5)
(3.5)
Ограничение (3.4) означает, что план всех работ должен быть выполнен полностью, а (3.5) означает, что ресурсы должны быть израсходованы целиком.
Примером этой задачи может быть задача о распределении самолетов по авиалиниям.
Задача о смесях. Имеется р компонентов, при сочетании которых в разных пропорциях получают разные смеси. Каждый компонент, а следовательно и смесь, содержит q веществ. Количество k-го вещества k = 1, 2,., q, входящее в состав единицы і-го компонента и в состав единицы смеси, обозначим через аik и аk соответственно.
Предположим, что аk зависит от аik линейно, то есть если смесь состоит из x1 единиц первого компонента, x2 - единицу второго компонента и т.д., то
![]()
Задано р величин Ci, характеризующих стоимость, массу или калорийность единицы i-го компонента, и q величин bk, указывающих минимально необходимое процентное содержание k-го вещества в смеси. Обозначим через x1, x2,.,xр значение компонента р-го вида, входящего в состав смеси.
Математическая модель этой задачи имеет такой вид:
 (3.6)
(3.6)
при ограничении
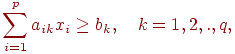 (3.7)
(3.7)
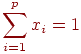
Ограничение (3.7) означает, что процентное содержание k-го вещества в единице смеси должно быть не меньше bk.
К этой же модели принадлежит также задача определения оптимального рациона кормления скота.
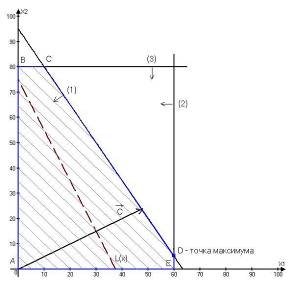
4. Геометрический метод решение задач ЛПЗадача 1. При откорме каждое животное должно получить не менее 14 ед.питательного вещества S1, не менее 15 ед. вещества S2 и не менее 10 вещества S3. Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 килограмме каждого вида корма и стоимость одного килограмма корма дана в таблице 1.
Таблица 1
| Питательные вещества | Количество единиц питательных веществ в 1 кг. корма | |
| корм 1 | корм 2 | |
| S1 | 1 | 2 |
| S2 | 1 | 3 |
| S3 | 2 | 1 |
| Стоимость 1 кг. корма | 3 | 7 |
Составить рацион минимальной стоимости.
Решение:
X1 + 2X2 ≥ 14
X1 + 3X2 ≥ 15
2X1 + X2 ≥ 10
X1, X2 ≥ 0
![]() 3X1 + 7 X2 → min
3X1 + 7 X2 → min
X1 + 2X2 = 14
X1 + 3X2 =15
2X1 + X2 = 10

5. Симплексный метод решения задач ЛП
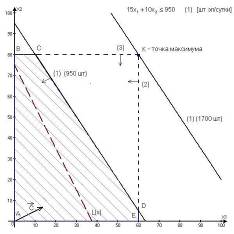
Задача 2. Для изготовления 4-ёх видов продукции P1, P2, P3, P4 используют два вида сырья: S1 и S2. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а так же величина прибыли, получаемая от реализации единицы продукции, приведены в таблице 2.
Таблица 2.
| Вид сырья | Запас сырья | Количество единиц сырья, идущих на изготовление единицы продукции | |||
| P1 | P2 | P3 | P4 | ||
| S1 | 3 | 1 | 1 | 1 | 2 |
| S2 | 7 | 1 | 2 | 3 | 1 |
| Прибыль от единицы продукции | 9 | 14 | 15 | 10 | |
Составить план производства, обеспечивающий получений максимальной прибыли.
Решение:
1. Формальная постановка задачи имеет следующий вид:
9X1 + 14X2 + 15 X3 + 10X4 → max
X1 + X2 + X3 + 2X4 ≤ 3
X1 + 2X2 + 3X3 + X4 ≤ 7
X1, X2, X3, X4 ≥ 0
2. Приведем к стандартной (канонической) форме:
F = 9X1 + 14X2 +15X3 + 10X4 + 0X5 + 0X6
X1 + X2 + X3 + 2X4 + X5 = 3
X1 + 2X2 +3X3 + X4 + X6 = 7
X1, X2, X3, X4 ≥ 0
3. Запишем систему ограничений в векторной форме:
X1 (1/1) + X2 (1/2) + X3 (1/3) + X4 (2/1) + X5 (1/0) + X6 (0/1) = (3/7)
P1 P2 P3 P4 P5 P6 P0
P5, P6 - базисные
4. Запишем первоначальный опорный план:
Х0 (0, 0, 0, 0, 3,7), F0 = 9*0 + 14*0 +15*0 +10*0 + 0*3 +0*7 = 0
Составим соответствующую плану 1 симплексную таблицу:
| Базис | Сб | Р0 | Р1 | Р2 | Р3 | Р4 | Р5 | Р6 |
| 9 | 14 | 15 | 10 | 0 | 0 | |||
| Р5 | 0 | 3 | 1 | 1 | 1 | 2 | 1 | 0 |
| Р6 | 0 | 7 | 1 | 2 | 3 | 1 | 0 | 1 |
| -9 | -14 | -15 | -10 | 0 | 0 | |||
Вычислим оценки:
∆ = (Сб*А) - С
∆1 = (0 *1 + 0*1) - 9 = - 9; ∆2 = (0 *1 + 0*2) - 14 = - 14; ∆3 = (0 *1 + 0*3) - 15 = - 15; ∆4 = (0 *2 + 0*1) - 10 = - 10; ∆5 = (0 *1 + 0*0) - 0 = 0; ∆6 = (0 *0 + 0*1) - 0 = 0
Критерием оптимальности является условие, что все ∆ ≥ 0, т.к. это не так, решение не оптимально.
Выберем вектор, который будем включать в базис:
min1 = (3/1; 7/1) = 3; min2 = (3/1; 7/2) =3; min3 = (3/1; 7/3) = 2 1/3; min4 = (3/2; 7/1) = 1 1/2,
теперь посмотрим соотношение min c ∆:
∆f = - ∆*min
∆f 1 = - (-9) *3 = 27; ∆f 2 = - (-14) *3 = 42; ∆f 3 = - (-15) *2 1/3 = 34.95; ∆f 4 = - (-10) *1 1/2 = 15,
Отсюда следует, что менять будем Р5 на Р2.
5. Составим 2 симплексную таблицу:
| Базис | Сб | Р0 | Р1 | Р2 | Р3 | Р4 | Р5 | Р6 |
| 9 | 14 | 15 | 10 | 0 | 0 | |||
| Р2 | 14 | 3 | 1 | 1 | 1 | 2 | 1 | 0 |
| Р6 | 0 | 1 | -1 | 0 | 1 | -1 | -1 | 1 |
| 5 | 0 | -1 | 4 | 14 | 0 | |||
7- (3*2) /1 = 1; 1 - (1*2) /1 = - 1; 3 - (2*1) /1 = 1; 1- (2*1) /1 = - 1; 0- (1*1) /1 = - 1; 1- (0*1) /1 = 1
∆1 = 14*1+0* (-1) - 9 = 5; ∆3 = 14*1+0*1-15 = - 1; ∆4 = 14*2+0* (-1) - 10 = 4;
∆5 = 14*1+0* (-1) - 0 = 14; ∆6 = 14*0+0*1-0 = 0;
Х1 (0,3,0,0,0,1); F1 = 9*0+14*3+15*0+10*0+0*0+0*1 = 42
Приняв этот план видим, что выпуск 2го вида продукции является наиболее выгодным, остаток сырья 2го вида продукции составит 1 единица.
Т.к. не все ∆ ≥ 0, план не является оптимальным, поэтому продолжим…..
Вектором Р3 заменим Р6 min = (3/1, 1/1) = (3,1)
Похожие работы
... среди математиков, его разделяли А.Н.Колмогоров, И.М.Гельфанд, В.И.Арнольд, С.П.Новиков и др. Нельзя не восхищаться естественностью и внутренней стройностью математической работ Л.В. по двойственности линейного программирования и их экономической интерпретацией. 2. О математической экономике как области математики и о некоторых ее связях А) Связи линейного программирования с функциональным и ...
... игр, теория массового обслуживания, и др. 1. ПОСТАНОВКА ЗАДАЧИ Целью нашего курсового проекта является решение задачи линейного программирования графическим методом. 1.1 Математическое программирование. Математическое программирование ("планирование") – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
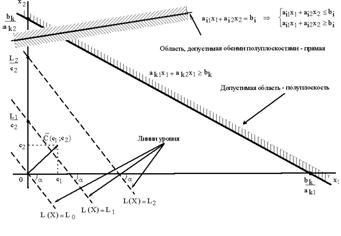
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
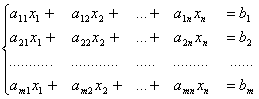
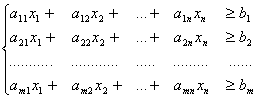





0 комментариев