Навигация
Методы построения функции принадлежности требований к заданному уровню качества
Методы построения функции принадлежности требований к заданному уровню качества
Существует значительное количество методов построения по экспертным оценкам функций принадлежности нечеткого множества m А(х). Выделяют две группы методов: прямые и косвенные методы.
Прямые методы характеризуются тем, что эксперт непосредственно задает правила определения значений функции принадлежности m А(х), характеризующей элемент х. Эти значения согласуются с его предпочтениями на множестве элементов Х следующим образом:
1. для любых х1, х2 Î Х m А(х1)<m А(х2) тогда и только тогда, когда х2 предпочтительнее х1, т.е. в большей степени характеризуется свойством А;
2. для любых х1, х2 Î Х m А(х1)=m А(х2) тогда и только тогда, когда х1 и х2 безразличны относительно свойства А.
Примерами прямых методов являются непосредственное задание функции принадлежности таблицей, графиком или формулой. Недостатком этой группы методов является большая доля субъективизма.
В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформулированным условиям. Экспертная информация является только исходной информацией для дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру обработки. Краткая характеристика наиболее часто используемых косвенных методов построения функций принадлежности.
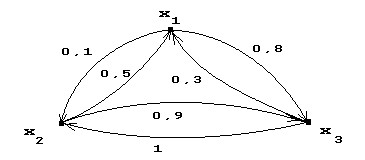
1. Построение функций принадлежности на основе парных сравнений
Метод основан на обработке матрицы оценок, отражающих мнение эксперта об относительной принадлежности элементов множеству или степени выраженности у них некоторого оцениваемого свойства.
Потребуем, чтобы для всех элементов множества А выполнялось равенство:
![]() (1)
(1)
Степень принадлежности элементов множеству А будет определятся посредством парных сравнений. Для сравнения элементов используются оценки, приведенные в таблице 1:
Таблица 1
| Интенсивность относительной важности | Определение |
| 1 | Равная важность сравниваемых требований |
| 3 | Умеренное (слабое) превосходство одного над другим |
| 5 | Сильное (существенное) превосходство |
| 7 | Очевидное превосходство |
| 9 | Абсолютное (подавляющее) превосходство |
| 2, 4, 6, 8 | Промежуточные решения между двумя соседними оценками |
Оценку элемента хі по сравнению с элементом хj с точки зрения свойства А обозначим через аij. Для обеспечения согласованности примем аij = 1/аji. Оценки аij составляют матрицу S = ║аij║.
Найдем W = (w1,...,wn) – собственный вектор матрицы S, решая уравнение
![]() , (2)
, (2)
где λ – собственное значение матрицы S.
Вычисленные значения, составляющие собственный вектор W, принимаются в качестве степени принадлежности элемента х к множеству А: m А(xi) = wi ; . Так как всегда выполняется равенство S∙W=n∙W, то найденные значения тем точнее, чем ближе λmax к n. Отклонение λmax от n может служить мерой согласованности мнений экспертов.
2. Построение функций принадлежности с использованием статистических данных
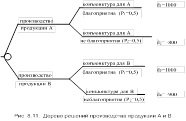
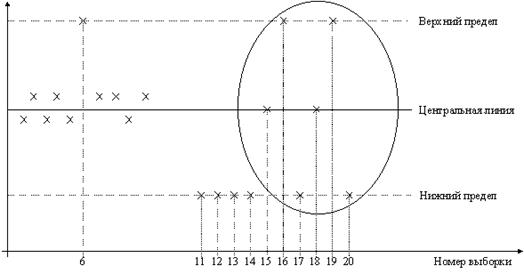
Предположим, что наблюдая за объектом в течение некоторого времени, человек n раз фиксирует свое внимание на том, имеет место факт А или нет. Событие, заключающееся в n проверках наличия факта А будем называть оценочным. Пусть в k проверках имел место факт А. Тогда эксперт регистрирует частоту p=k/n появления факта А и оценивает ее с помощью слов "часто", "редко" и т.п.
На универсальной шкале [0,1] необходимо разместить значения лингвистической переменной: Весьма редко, более – менее редко, более менее часто, весьма часто. Тогда степень принадлежности некоторого значения вычисляется как отношение числа экспериментов, в которых оно встречалось в определенном интервале шкалы, к максимальному для этого значения числу экспериментов по всем интервалам. Метод требует выполнения условия, чтобы в каждый интервал шкалы попадало одинаковое число экспериментов. Если это условие не выполняется, требуется дополнительная обработка экспериментальных данных с помощью так называемой матрицы подсказок.
Похожие работы
... выходных лингвистических переменных. С помощью правил преобразования дизъюнктивной и конъюнктивной формы описание системы можно привести к виду: L1 : если <A1 > то <B1 >, L2 : если <A2 > то <B2 >, .................... Lk : если <Ak > то <Bk >, где A1,A2,..,Ak - нечеткие множества, заданные на декартовом произведении X универсальных множеств входных ...
... задач за счет применения средств автоматизации, снижение затрат за счет сокращения штата сотрудников, привлекаемых к делопроизводству, поиску и сортировке управленческой документации за счет внедрения электронного документооборота и т.д.) Результаты второго рода могут быть измерены с помощью экономических показателей, находящихся в бухгалтерской отчетности. Доход третьего рода получают за счет ...
... и инструментов, используемых в течение всего жизненного цикла продукции для планирования потребительной стоимости продукции и обеспечения требуемого уровня качества процессов 2 Анализ качества продукции на заводе полистиролов ОАО «Нефтекамскнефтехим» 2.1 Общая характеристика деятельности предприятия ОАО "Нефтекамскнефтехим" - динамично развивающееся, высокотехнологичное нефтехимическое ...
... Система управления качеством должна строится на определенных принципах, то есть системе правил, норм, основных положений, которыми следует руководствоваться при управлении качеством продукции. Пренебрежение этими принципами приводит к потере эффективности процесса совершенствования деятельности предприятия. Рассмотрим основные принципы управления качеством. Принцип системности: система ...
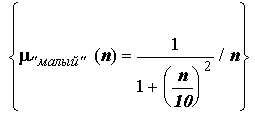
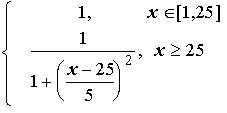

0 комментариев