Навигация
Построение функций принадлежности на основе экспертных оценок
3. Построение функций принадлежности на основе экспертных оценок
Рассмотрим особенности построения функций принадлежности для приближенных точечных (например, Х приблизительно равен 10) и интервальных оценок (вида Х находится приблизительно в интервале от 8 до 11). Естественно предположить, что функцию, необходимо строить следующим образом:
если α ≤ х ≤ β, то μ(α, β) (х) = 1;
если х < α, то μ(α, β) (х) = μα (х);
если х < β, то μ(α, β) (х) = μβ (х),
где μ(α, β) (х) – функция принадлежности нечеткому интервалу (α, β);
μα(х) и μβ(х) – функции принадлежности нечетким множествам чисел, приближенно равных соответственно α и β.
При построении функции принадлежности чисел, приблизительно равных некоторому k, можно использовать функцию
![]() (3)
(3)
где α зависит от требуемой степени нечеткости μk(х), и определяется из выражения
![]() (4)
(4)
где b - расстояние между точками перехода для μk(х), т.е. точками, в которых функция вида принимает значение 0,5.
Таким образом, задача построения μk(х) для некоторого числа сводиться к отысканию параметров а и в, чтобы можно было определить β (х), с помощью β(х) – α θ, используя α, построить μk(х).
4. Параметрический подход к построению функций принадлежности
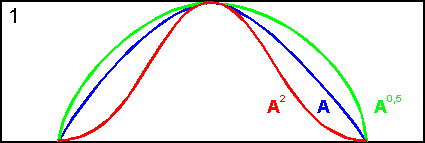
Описываемый метод построения функций принадлежности основан на предположении, что эксперт характеризуя лингвистическое значение какого-либо признака, с минимальным напряжением может указать три точки шкалы: А, В, С, из которых В и С – точки, по его мнению, еще (или уже) не принадлежащие описываемому лингвистическому значению, А – точка, определенно принадлежащая ему.
Пусть имеются параметрическое описание термов t и tI двух значений некоторой лингвистической переменной. Один из термов может представлять собой модификацию (ограничение) другого: tI = h (t), где h – ограничение на t типа ДОВОЛЬНО, БОЛЕЕ – МЕНЕЕ, НЕ ОЧЕНЬ и т.п. Задача состоит в том, чтобы используя параметры термов t: (z1, z2, z3) и tI: (ω1, ω2, ω3) описать переход от t к tI (параметры считаются упорядоченными отношением "меньше").
Очевидно, что S – образную функцию можно рассматривать, как вырожденный случай треугольной функции, в которой один из параметров z1 или z2 стремится к бесконечности. Таким образом, задача состоит в том, чтобы описать переход между любыми двумя формами
Для решения этой задачи используется аппарат автоморфных функций. Рассмотрим дробно-линейное отображение прямой на себя вида
![]() (5)
(5)
преобразование Т-1, обратное Т, получается, если уравнение
![]()
разрешить относительно ω:
![]() (6)
(6)
Таким образом, при параметрическом представлении функций принадлежности задача описания перехода от одного терма t: (z1, z2, z3) к другому tI: (ω1, ω2, ω3) решается непосредственным подсчетом четырех параметров – коэффициентов дробно-линейного преобразования по формулам:
 (7)
(7)
Эти же коэффициенты при подстановке в (6) определяют обратный переход от tI к t.
Рассмотрим теперь переход от терма t треугольной формы к терму tI с S – образной функцией принадлежности. Для дробно-линейных преобразований этому случаю соответствует переход от одной из крайних заданных точек в положение бесконечно-удаленной точки.
Если z1 = ∞, то параметры дробно-линейного преобразования
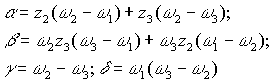 (8)
(8)
Если z3 = ∞ , то
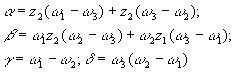 (9)
(9)
Рассмотрим случай, когда функции принадлежности представляются S – образной или просто наклонной кривой. В этом случае имеет место линейное отображение прямой
![]() (10)
(10)
Параметры преобразования (10)
![]() (11)
(11)
Обратный переход (у → х) осуществляется по формуле
![]() (12)
(12)
5. Построение функции принадлежности на основе ранговых оценок
Данный метод разработан А.П. Ротштейном и базируется на идее распределения степени принадлежности элементов универсального множества согласно с их рангами.
Будем понимать под рангом элемента хіÎ Х число rs(xi), которое характеризует значимость этого элемента в формировании свойства, которое описывается нечетким термом . Допускаем, что выполняется правило: чем больший ранг элемента, тем больше степень принадлежности.
Введем также обозначения:
![]()
Тогда правило распределения степеней принадлежности можно задать в виде соотношения:
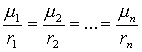 (13)
(13)
к которому добавляется условие нормирования
![]() (14)
(14)
Используя соотношение (13) легко определить степени принадлежности всех элементов универсального множества через степени принадлежности опорного элемента.
Если опорным элементом является элемент х1 Î Х с принадлежностью m 1, то
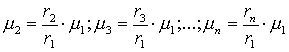 (15)
(15)
Для опорного элемента х2 Î Х с принадлежностью m 2, получаем
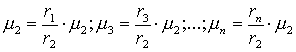 (16)
(16)
Для опорного элемента хn Î Х с принадлежностью m n, имеем
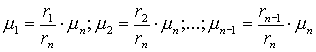 (17)
(17)
Учитывая условие нормировки (14) из соотношений (15) – (17) находим:
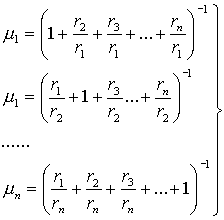 (18)
(18)
Полученные формулы (18) дают возможность вычислять степени принадлежности m S(xi) двумя независимыми путями:
- по абсолютным оценкам уровней ri ![]() , , которые определяются по 9-ти бальной шкале (1 – наименьший ранг, 9 – наибольший ранг).
, , которые определяются по 9-ти бальной шкале (1 – наименьший ранг, 9 – наибольший ранг).
- по относительным оценкам рангов
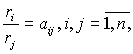
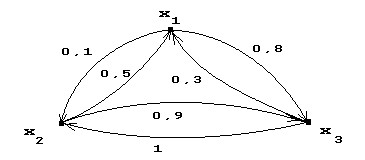
которые образуют матрицу:
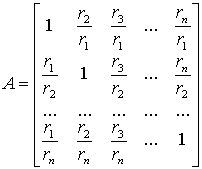 (19)
(19)
Эта матрица обладает следующими свойствами:
а) она диагональная, т.е. аiі=1 ![]() ;
;
б) элементы, которые симметричны относительно главной диагонали, связаны зависимостью: аij=1/аji;
в) она транзитивна, т.е. аiк× акi, поскольку
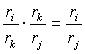
Наличие этих свойств приводит к тому, что при известных элементах одной строки матрицы А легко определить элементы всех других строк. Если известна r-я строка, т.е. элементы акj, k ![]() , , то произвольный элемент аij находиться так
, , то произвольный элемент аij находиться так ![]()
Поскольку матрица (19) может быть интерпретирована как матрица парных сравнений рангов, то для экспертных оценок элементов этой матрицы можно использовать 9 – ти бальную шкалу Саати: . Эта шкала приведена ранее, в табл. 1.
Таким образом, с помощью полученных формул (6.5.18), экспертные значения о рангах элементов или их парные сравнения преобразуются в функцию принадлежности нечеткого терма.
Алгоритм построения функции принадлежности включает в себя следующие операции:
1. Задать лингвистическую переменную;
2. Определить универсальное множество, на котором задается лингвистическая переменная;
3. Задать совокупность нечетких термов {S1, S2, ... , Sm}, которые используются для оценки переменной;
4. Для каждого терма Sj ![]() , сформировать матрицу (19);
, сформировать матрицу (19);
5. Используя формулы (18) вычислить элементы функций принадлежности для каждого терма.
Нормирование найденных функций осуществляется путем деления на наибольшие степени принадлежности.
Главным преимуществом метода является то, что в отличие от метода парных сравнений, он не требует решения характеристического уравнения. Полученные соотношения дают возможность вычислять функции принадлежности с использованием ранговых оценок, которые достаточно легко получить при экспертном опросе.
Кроме описанных методов построения функций принадлежности, нашедших наиболее широкое практическое применение, имеется еще значительное число методов, описанных в литературе (метод интервальных оценок, метод семантического дифференциала и т.д.).
При выборе метода необходимо учитывать, как правило, сложность получения экспертной информации, особенно организации и проведения экспертизы, достоверность экспертной информации, трудоемкость алгоритма обработки информации при построении функции принадлежности.
В нашем случае функция принадлежности m (xi,j), входящая в формулу (4) для оценки качества системы защиты информации, характеризует лингвистическую переменную "степень выполнения j-го требования при защите от i-ой угрозы". В заключение рассмотрим пример построения функции принадлежности m (хij)=m (xi) методом Ротштейна.
Рассмотрим лингвистическую переменную "качество", характеризуемое степенью выполнения некоторого требования. Эта лингвистическая переменная определена на универсальном множестве вариантов: хі, ![]() . Уровень качества будем оценивать такими нечеткими термами: Н – низкий; С – средний; В – высокий.
. Уровень качества будем оценивать такими нечеткими термами: Н – низкий; С – средний; В – высокий.
Пусть в результате экспертного опроса сформированы матрицы (19) для каждого терма. При сравнении вариантов используется табл. 1.

матрица статистический ранговый лингвистическая переменная
После обработки этих матриц по формулам (18) получим функции принадлежности.
Похожие работы
... выходных лингвистических переменных. С помощью правил преобразования дизъюнктивной и конъюнктивной формы описание системы можно привести к виду: L1 : если <A1 > то <B1 >, L2 : если <A2 > то <B2 >, .................... Lk : если <Ak > то <Bk >, где A1,A2,..,Ak - нечеткие множества, заданные на декартовом произведении X универсальных множеств входных ...
... задач за счет применения средств автоматизации, снижение затрат за счет сокращения штата сотрудников, привлекаемых к делопроизводству, поиску и сортировке управленческой документации за счет внедрения электронного документооборота и т.д.) Результаты второго рода могут быть измерены с помощью экономических показателей, находящихся в бухгалтерской отчетности. Доход третьего рода получают за счет ...
... и инструментов, используемых в течение всего жизненного цикла продукции для планирования потребительной стоимости продукции и обеспечения требуемого уровня качества процессов 2 Анализ качества продукции на заводе полистиролов ОАО «Нефтекамскнефтехим» 2.1 Общая характеристика деятельности предприятия ОАО "Нефтекамскнефтехим" - динамично развивающееся, высокотехнологичное нефтехимическое ...
... Система управления качеством должна строится на определенных принципах, то есть системе правил, норм, основных положений, которыми следует руководствоваться при управлении качеством продукции. Пренебрежение этими принципами приводит к потере эффективности процесса совершенствования деятельности предприятия. Рассмотрим основные принципы управления качеством. Принцип системности: система ...
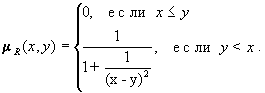

0 комментариев