Кореляційно-регресійний аналіз впливу факторів на формування прибутку нафтопереробних підприємств

2. Кореляційно-регресійний аналіз впливу факторів на формування прибутку нафтопереробних підприємств

Дослідження прибутку та його динаміки в галузі нафтопереробки України проводилось у двох основних спрямуваннях: економіко-статистичний аналіз зв’язків результатів ( прибутку) з факторами впливу і моделювання в системі управління прибутками. Порівняльний економіко-статистичний аналіз прибутку основних нафтопереробників України було зроблено з застосуванням відомих статистичних методів з підключенням спеціальних офісних генераторів Excel. Другий напрям формальних досліджень було реалізовано на підставі математичного багатопараметричного моделювання, що включали створення математичної моделі управління прибутками і її машинної реалізації у вигляді автоматизованої системи.

У якості об’єктів порівняльного аналізу нами розглядалися чотири нафтопереробних завода: Херсонський нафтопереробний завод, нафтопереробний завод "Галичина", нафтопереробний завод "Нафтохімік Прикарпаття", "Лукойл-Одеський нафтопереробний завод", де досліджувалися динамічні ряди показників фінансової діяльності у період 1999 – 2004 роки.

Оскільки досліджувані об’єкти є складними та великими економіко-виробничими системами, то логічним є те, що аналіз проводився на основі системних підходів з використанням методів системного аналіза.

Зазначимо, що традиційним предметом дослідження таких систем є управлінські функції з метою пошуків закономірностей процесів, формалізації їх системних властивостей, т.б. виявлення зв’язків та взаємозв’язків елементів систем. Для цього виправдано спираються на основні положення теорії систем, системний аналіз.

Інформаційною базою у нашому випадку були дані фінансових звітів по основним напрямкам господарської діяльності.

Вимоги системності при дослідженні виробничо-економічних об’єктів припускають на попередніх етапах спеціальну організацію даних у вигляді аналізу зв’язків на основі використання статистичних методів обробки інформації.

Оскільки ми будемо мати справу з моделями різних типів, то оцінку адекватності моделей будемо здійснювати за допомогою оцінки адекватності складових. Будь-яке економічне дослідження починається зі специфікації моделі , т.б. з формування виду моделі, спираючись на відповідну систему зв’язків між змінними. Зв’язок змінних x та y описується коефіцієнтом кореляції , який визначається як коваріація між цими змінними віднесена до їх середніх відхилень:

, або

Зауважимо при цьому, що у якості міри тісноти зв’язку між параметрами часто використовують індекс кореляції, який у випадку наявності лінійної залежності має наступний вираз:  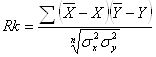та у випадках нелінійного зв’язку: 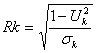де,

- середнє квадратичне відхилення від кривої;

- середнє квадратичне відхилення функції від свого середнього арифметичного значення.

На практиці дослідження залежностей між випадковими змінними х та у, як правило, обмежені дослідженням залежності між однією з них і умовним математичним сподіванням іншої, т.б. умовне математичне сподівання випадкової змінної у розглядається як функція х;

Цей вираз має назву регресії випадкової змінної y відносно x. Аналогічно  - випадкова величина х, як функція від у, т.б.:. У цьому випадку функція регресії буде характеризувати форму зв’язку. Криву регресії у по х (або навпаки) називають умовне середнє значення випадкової змінної у, яке розглядається як функція певного класу, параметри якої знаходяться методом найменших квадратів (МНК) за значеннями двувимірної випадкової величини (x,y), що спостерігаються т.б.:, . На практиці передумови кореляційного аналізу часто порушуються, коли одна з ознак є величиною не випадковою, або якщо ознаки не мають спільного нормального розподілу, але статистичні залежності присутні. В цьому випадку для вивчення зв’язків між ознаками існує загальний показник зв’язку ознак, який грунтується на показнику змінності. Цей показник називається дисперсією. Звичайно дисперсію ознаки відносно його математичного сподівання називають повною. Наприклад, для ознаки у дисперсія буде мати наступний вигляд: . Дисперсію можна розкласти на дві складові, одна з яких буде характеризувати вплив фактора х на у, друга – вплив інших факторів. Чим меншим є вплив інших факторів, тим тісніше є зв’язок, тим щільніше він наближується до функціонального зв’язку. Якщо ми запишемо:

,

то перша складова вимірює вплив х на у, а друга - вимірює вплив на у інших факторів(дисперсія ознаки у відносно функції регресії).

Тісноту зв’язку вдало оцінювати в одиницях загальної дисперсії , тобто розглядати співвідношення:

.

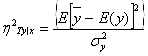На початковому етапі ми встановили парні кореляційні залежності, як різновид структурного моделювання. Потреба у причинному поясненні наявності або відсутності кореляційних зв’язків було підгрунтям для використання "методу путєвого аналізу"(С.Райт), в основі якого дослідження всієї структури чинних зв’язків між змінними (побудова графіка зв’язків та ізоморфної до нього рекурсивної системи рівнянь). Оцінка коефіцієнта впливу у цьому випадку розраховується на базі коефіцієнта парної кореляції. Кожний коефіцієнт парної кореляції розглядався нами як міра повного зв’язку двох змінних. Наявність і якість парних зв’язків показників фінансової діяльності встановлювались по кожному підприємству і по кожному показнику фінансової діяльності. Кореляційні відносини між показниками фінансових потоків, які мають вираз у вигляді коефіцієнтів кореляції і залишків надали змоги встановити наявність зв’язку та міру його тісноти. Так, по Херсонському нафтопереробному комплексу з усіх показників, які аналізувалися, найбільш тісні кореляційні відносини зафіксувалися між показниками чистого доходу та сумарними відрахуваннями, собівартістю та іншими операційними доходами (табл 2.11). Характерним є те, що виручка від реалізації продукції практично з усіма показниками, які було проаналізовано або взагалі не має кореляційного зв’язку, або має з ними від’ємну залежність.

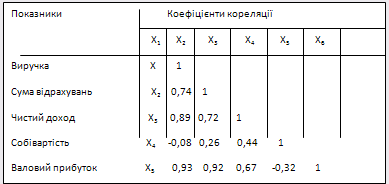
Таблиця 2.11 Матриця парних коефіцієнтів кореляції показників фінансової діяльності Херсонського нафтопереробного заводу

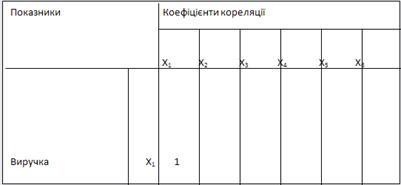
Слід відмітити, що кореляційні зв’язки між чистим прибутком і рештою показників, що аналізувалися менш тісні у порівнянні з тіснотою зв’язків між чистим доходом і рештою показників (R=0,6-0,66).

При встановленні кореляційних відносин між фінансовими потоками нафтопереробного комплексу "Галичина" (табл. 2.12 ) найбільш тісна позитивна кореляційна залежність спостерігається з такими фінансовими показниками як: валовий прибуток і виручка та від’ємна залежність між показниками валового прибутку та виручки з собівартістю. Чистий доход позитивно корелює з валовим прибутком (R=0,67) .

Таблиця 2.12 Матриця парних коефіцієнтів кореляції показників фінансової діяльності НПК "Галичина"

Характерним для "Нафтохіміка Прикарпаття" як і для "НПЗ-Галичина" є значна кількість від’ємних кореляційних залежностей . Так із загальної кількості парних коефіцієнтів кореляції у інтервалі  у кількості 25 показників тільки 32% є позитивними (табл. 2.13).

Таблиця.2.13 Матриця парних коефіцієнтів кореляції показників фінансової діяльності ВАТ "Нафтохімік Прикарпаття"

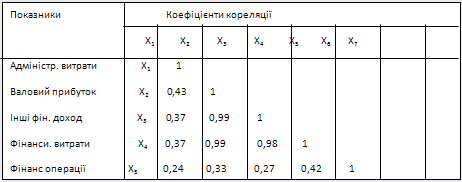
Валовий прибуток позитивно корелює з іншими фінансовими доходами (R=0,99) та фінансовими витратами (R=0,99). Показники інших фінансових доходів та фінансових витрат також пов’язані між собою тісною кореляційною залежністю (R=0,98).

Щодо аналізу фінансових показників нафтопереробного підприємства "Лукойл-Одеський нафтопереробний завод", то на відміну від раніше аналізованих нафтопереробних підприємств, цей об’єкт нашого дослідження має велику кількість парних позитивних кореляційних зв’язків між складовими показниками формування фінансового результату.

Таблиця 2.14 Матриця парних коефіцієнтів кореляції показників фінансової діяльності ВАТ "Лукойл"

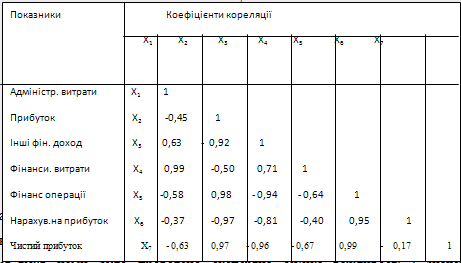
Чистий прибуток, наприклад, тісно корелює з усіма параметрами, які аналізувалися (R=0,78 – 0,98). Вся решта показників має високий коефіцієнт кореляції між собою та чистим прибутком. Окрім встановлення тісноти зв’язків нами було проведено експертна оцінка важливості і значень параметрів аналізу методом парних порівнянь(табл 2..15).

Таблиця 2.15 Вагові коефіцієнти експертного оцінювання

	Х1	Х2	Х3	Х4	å
Х1	0,4	0,3	0,1	0,2	1
Х2	0,2	0,3	0,1	0,4	1
Х3	0,3	0,2	0,1	0,4	1
Х4	0,4	0,2	0,1	0,3	1
Сер.знач.	0,325	0,25	0,1	0,325
Сер.кв.відх.	0,08	0,05	0,00	0,08
Дисперсія.	0,01	0,00	0,00	0,01
Коваріація.	0,23	0,20	0,00	0,23

Встановлено, що серед аналізуємих параметрів фінансових потоків найбільш важливими для підприємств (впливовими) за оцінками експертів були: чистий дохід від реалізації – Х₁, собівартість продукції – Х₂, фінансові витрати – Х₃, податок на прибуток – Х₄. Серед визначених показників найбільший ваговий коефіцієнт припадає на чистий дохід від реалізації продукції. Оцінка за питомою вагою значень коефіцієнтів кореляції показала, що найбільш високий індекс важливості припадає на виручку від реалізації та на чистий прибуток при досить низьких значеннях коваріаційних відносин. Аналіз на підставі попарного порівняння за цими показниками підприємств вказує на переваги Херсонського НПЗ.

Парна кореляційна залежність дає уявлення про наявність та тісноту зв’язків серед змінних, які приймали участь у аналізі. Але більш точний порівняльний аналіз фінансових потоків, що притаманні об’єктам нашого дослідження, може надати регресійний аналіз, коли значення залежної змінної розглядають як функцію від незалежної.

Тобто, якщо основна задача кореляційного аналізу, що проведено нами є виявлення зв’язків між випадковою змінною шляхом точкової інтервальної оцінки парних коефіцієнтів кореляції, то основною задачею застосування функцій регресії стало вивчення залежності між результативними ознаками у(роки) та ознакою х (параметри фінансових потоків) , що спостерігається.

При цьому помітимо, що попередній аналіз вхідного матеріалу з використанням графічного інструментаря показав практичну відсутність лінійних трендів, хоча в класичних підходах до статистичного аналізу саме вони (лінійні тренди) і є найбільш реалістичним сценарієм. У своїй більшості ми маємо нелінійні залежності по змінній x.

Для повноти аналізу ми досліджували наступні типи функцій, що описують нелінійні відносини: нелінійні відносно включених до аналізу пояснюючих змінних та нелінійні за параметрами, які оцінюються.

Виокремлюючи з масивів даних фінансових потоків параметри з найбільш тісними фінансовими відносинами ми досліджували та обирали найбільш прийнятну форму рівняння регресії з метою наступного прогнозу змін конкретного фінансового потоку. При цьому досліджувались:

Рівнобічна парабола: ; Парабола другого ступеню: ²; Поліномінальні рівняння: Степеневі рівняння:^bִ;

Показові функції: ^xִ;

Експоненціальні функції:^ִ.

Логарифмічні:

Вибір виду рівняння відбувався методом експертного оцінювання, тобто порівнянням величин остаточної дисперсії. Зауважимо, що у багатьох випадках аналізу парних лінійних зв’язків мав місце значний розсів точок відносно лінії регресії. Така ситуація пов’язана з впливом факторів, що не були враховані. За критерії використання моделей брались фінансові ситуації що склалися у виробничої діяльності НПЗ в динаміці, їх коефіцієнти значущості за експертними оцінками і придатність до прогнозування процесів на підставі моделювання.

Для більш повної класифікації моделей, які було використано, доречно зауважити, що нелінійні моделі прийнято поділяти на моделі внутрішньо лінійні і внутрішньо не лінійні. Сутність полягає у тому, що внутрішньо лінійні моделі за допомогою відповідних перетворень можуть бути приведені до лінійних; моделі внутрішньо не лінійні не можуть бути приведені до лінійного вигляду. Так, наприклад, степенева функція відносно параметрів, що ми оцінювали є не лінійною, оскільки включає a, b не адитивна. Однак, ця функція внутрішньо лінійна, оскільки логарифмування по основі e призводить до лінійного вигляду: ;

Навпаки, модель яка представлена як  внутрішньо нелінійна, оскільки у лінійний вигляд її перетворити неможливо. Моделі типу

 та

які ми використовували також є нелінійними внутришньо, у той час як експонента  відноситься до внутрішньо лінійній, так як логарифмування її по e дає лінійну форму зв’язків:.

У якості вступу до аналізу необхідно звернути увагу на наступне. Під час праці з часовими рядами різних показників та при дослідженні зв’язків між ними необхідно ураховувати проблему хибної кореляції та проблему зрушень у часі (лаги).

У часових рядах, що корелюються хибна кореляція виникає під впливом так званої трендової компоненти. Це є причиною того, що у лінійних трендах вимірюють не рівні змінних X_i, Y_i а їх різницю :

;

Якщо структуру часового ряду розглядати як таку, що складається з тренда T_i, кон’юнктурного циклу – К, сезонної компоненти – S, залишкової компоненти R, то динамічний ряд можна зобразити як суму цих компонент.

Тобто часові ряди показників х і у можна записати:

; ;

О. Андерсон запропонував вимірювати взаємозв’язки між цими компонентами рядів та вишукувати між ними окремі коефіцієнти кореляції:

-  якщо тренди обох рядів дуже виражені та мають однакову спрямованість, то кореляція набуває великого значення;

-  якщо тренди різноспрямовані, то кореляція може бути значна за величиною, але від’ємна за значенням;

-  кореляція між компонентами визначається тіснотою зв’язку між трендами та кон’юнктурними коливаннями, між трендами та сезонною компонентою і т.інш.

Головним у нашому аналізі регресійних моделей було те положення, що функція регресії може бути використана для прогнозування однієї з випадкових змінних, якщо відомо значення іншої випадкової змінної.

Тобто, у якості критеріїв використання моделей нами було обрано фінансові ситуації, які склалися у господарський діяльності нафтопереробних заводів, а також можливість прогнозування процесів на основі моделювання.

Виробничі функції, які описують динаміку основних фінансових потоків в досліджуваному періоді (1999-2004) наведені у додатках "В1-В5".

На основі використання не лінійних функцій регресії з метою прогнозування досліджувалися ряди динаміки фінансових процесів, які виражені окремими параметрами.

Попередньо виділимо статистичні показники, що були покладені в основу інтегральної оцінки:

1.Середній коефіцієнт прирощення

2.Загальна та залишкова дисперсія -

3.Коефіцієнти парної та множинної кореляції

4.Індекси кореляції

Як витікає з попереднього аналізу, ряди показників фінансових потоків за об’єктами дослідження залежні, а деякі з них мають достатньо складний вигляд. Для таких рядів динаміки , як правило, характерна висока автокорельованість. Тільки завдяки правильному підбору функцій нам вдалося запобігати цьому явищу. Як наслідок, і було використане нами таке різноманіття функцій.

Відхилення фактичних значень показників фінансових потоків від значень, що визначаються на основі згладженої функції характеризують варіацію ряду, яка не пов’язана з основною вірогіднісною тенденцією. Це дає можливість застосувати для оцінки прогнозу характеристики на основі використання відомого апарату математичної статистики та теорії вірогідності.

Підкреслимо, що не всі функції, які відібрані нами можуть використовуватися для прогнозування, тобто, не по кожній з них можливо продовжити тенденцію , яка склалася на найближчу перспективу і знайти найбільш вірогідні обмеження відхилень фінансових потоків, що прогнозуються.

В цьому випадку, якщо відсутнє прирощення значень показників у прогнозний період, використовується логічний аналіз згладжуваних і продовжуваних значень на базі графічних зображень.

Графічне зображення залежностей, які апроксимують дані рівнянь у вигляді трендів для умов Херсонського НПЗ, Львівського НПЗ, Івано-Франківського НПЗ, Одеського НПЗ, дає можливість спостерігати і робити висновки відносно залежності між показниками, що включені до аналізу.

Іншими словами, метод що ми вибрали можна вважати надійним для прогнозування тенденцій стану параметрів фінансової діяльності.

Оскільки у нашому аналізі використані практично всі придатні для нашого випадку типи регресійних моделей має сенс підкреслити деякі особливості. Найчастіше для очікування множинних зв’язків фінансових параметрів об’єктів, що досліджуються, сприяли поліномінальні регресії.

Параболи другого ступеня були більш доцільними у випадках, коли для певного інтервалу значень фактора змінювався характер зв’язку ознак, що розглядаються (прямий на зворотній і навпаки). У цьому випадку використовувалося (для прогнозу) значення фактору за яким було досягнуто максимальне або мінімальне значення результативної ознаки.

Параболічний тренд, краще апроксимуючий вхідні дані, в цьому випадку можна прийняти як оптимістичний сценарій, але у практичних ситуаціях ринкових відносин зростання не може бути постійно прискореним. За умови оздоровлення економіки параболічний сценарій є можливим.

У випадках коли у даних не спостерігали зміни спрямованості зв’язку, параметри параболи другого порядку ставало важко інтерпретувати. Тоді форма зв’язку замінювалася іншими нелінійними моделями, параметри яких можуть бути оцінені за допомогою методу найменьших квадратів.

Сутність методу найменьших квадратів полягає у наступному. Якщо ми за нелінійній залежності по змінній х запишемо:

,

тоді оцінкою цього виразу буде регресія:

,

де b₀ ,b₁ - є оцінками коефіцієнтів регресії β₀ і β₁. Коефіцієнти знаходяться з виразу:

Диференціюючи по та шляхом віднесення правих частин до нуля отримуємо систему нормальних рівнянь:

Оскільки досліджувані виробничі об’єкти мають різне економічне становище, при цьому маючи схожу за номенклатурою продукцію, логічним буде провести порівняльний аналіз придатності тих чи інших моделей для прогнозу фінансового стану.

У наших дослідженнях при строгому підборі функцій домінуючими були поліномінальні функції більші ніж другого порядку, які характеризують найбільш тісні зв’язки і краще вирівнювали, а в деяких випадках і страчували автокореляцію.

Якщо спиратися на значення R² то прибуток апроксимується з параболою другого і вище порядків, або з експоненціальною функцією практично однаково.

Безумовний інтерес викликає дослідження крім прибутку, тенденції інших показників фінансового стану підприємств які відносяться до операційної діяльності.

На деяких підприємствах цей процес може бути описано параболою другого порядку (Херсон, Лукойл), для інших (Прикарпаття, Галичина) він краще апроксимується логарифмічними або експоненційними функціями і чіткіше показує тенденцію до збільшення прогнозного показника .

Таблиця 2.16 Основні функції прогнозування значень показників діяльності об’єктів досліджень.

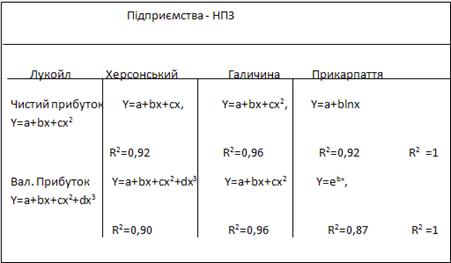
Відносно інших показників, то виробничі доходи більш надійно апроксимувалися степеневою та експоненціальною функціями.

Характерним в цьому процесі є те, що степенева та експоненціальна моделі більш привабливі для динамічних рядів фінансових потоків витратних статей звіту відносно фінансових результатів.

Серед основних фінансових показників економічної ефективності діяльності НПЗ: для ХНПЗ характерними є поліноми, для НПК "Галичина" – функцію прибутку краще за все описує парабола, для НПЗ "Нафтохімік Прикарпаття" кращими прогнозними моделями стали логарифмічні та експоненціальні, для НПЗ "Лукойл – Одеський нафтопереробний завод" – поліноми другого та третього порядків.

Може викликати стурбованість і, як слідство, необхідність в більш розширеному і глибокому економічному аналізі більшості досліджуваних нами об’єктів, результатів їх діяльності, це наявність тенденцій зниження фінансових показників і зокрема прибутку, що характерно для більшості з досліджуваних об’єктів. Така тенденція обумовлена і пов’язана з загальною економічно-соціальною ситуацією в Державі. Наявність невизначеностей, їх поширеність і неможливість формального опису ускладнюють прогнозування на підставі трендових оцінок.

Переслідуючи мету найбільш коректного аналізу впливу факторів на фінансові показники виробничої діяльності, ми встановили міжпараметричні зв’язки показників фінансових потоків на підприємствах і побудували багатопараметричні моделі прогнозу, де відображено окрім прямої участі досліджуваних факторів і ефект їхнього взаємовпливу.

Багатопараметрична регресія є найбільш поширеним методом у економічних системах у разі їх аналізу і управління. Основна мета множинної регресії – створити модель з необхідною кількістю факторів, визначивши вплив кожного з них окремо і у сукупної дії на показник, що моделюють.

Будь які економічні дослідження слід починати зі специфікації обраної моделі, т.б. формування її виду, виходячи з відповідної теорії між змінними.

На основі вимоги конфліентного аналізу необхідно знати всю сукупність зв’язків між змінними. Змінна буде вважатися корисною, якщо її включення підвищує дисперсію. Якщо введення нової змінної не змінює коефіцієнт при інших змінних, вона вважається зайвою, а якщо додавання змінної дуже змінило , без помітної зміни коефіцієнта кореляції, - то вона вважається шкідливою.

Безсумнівну зацікавленість, у нашому випадку, викликає оцінка зв’язку одного з показників з іншими, що входять до складу параметрів які характеризують досліджувані нами процеси. Досягається це з допомогою множинного або сукупного коефіцієнта кореляції:

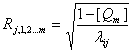, де

Q_m – визначник кореляційної матриці

λ_ij – алгебраїчне доповнення до елементів R_ij

У випадку, коли ми маємо m математичних сподівань та m дисперсій,

m(m–1)/2 парних коефіцієнтів кореляції, будемо мати багатомірний кореляційний аналіз, де часний коефіцієнт кореляції L-го порядку на випадок m ознак можна буде знайти з кореляційної матриці.

Багатовимірний кореляційний аналіз дозволяє отримати оцінку функції регресії. Цей аналіз буде мати місце, якщо вимірювання результативної ознаки визначається дією сукупності інших ознак.

У випадку заміни параметрів їх оцінками будемо мати рівняння :

, де вільний член та коефіцієнти b₁…b_m знаходять методом найменших квадратів (МНК). Вихідною є вибірка з багатовимірної сукупності показників фінансових потоків у вигляді матриці Х і вектора У.

А. Багатопараметричні моделі зв’язку основних показників фінансової діяльності НПЗ

Змінні моделей по НПЗ Херсон:

Х₁ - валовий дохід від виробничої діяльності

Х₂ – виручка від реалізації

Х₃ – собівартість продукції

Х₄ – валовий прибуток

Х₅ – інші операційні доходи

Х₆ – нарахування

Х₇ – чистий прибуток

Виробничі функції зв’язку параметрів

Y=2755,6 – 0,113X₁+0,136X₂+0,005X₃ – 0,83X₄+0,13X₅+0,78X₆

Y=29297,6 – 0,04X₁-0,0009X₂-0,017X₃+0,013X₅+0,09X₆+1,29X₇

Y=56721,9 – 2,65X₄+0,26X₂+0,77X₃+0,28X₅+1,67X₆+0,34X₇

Y=159707 – 0,11X₄+0,37X₁- 0,29X₃- 0,90X₅-5,17X₆+15,26X7

Змінні моделей по НПК "Галичина"

Х₁ - виручка від реалізації

Х₂ – суми відрахувань

Х₃ – чистий прибуток

Х₄ – собівартість продукції

Х₅ – валовий прибуток

Х₆ – інші операційні доходи

Виробничі функції зв’язку показників діяльності.

Y=30810,2+3,61X₂-0,19X₃+0,44X₄-0,06X₅-0,0002X₆

Y=243075,1-0,32X₁+0,80X₂-1,05X₄+3,30X₅+1,42X₆

Y=-50969,1+0,197X₃+0,09X₁+0,29X₂+0,12X₄+0,33X₆

Б. Багатопараметричні моделі фінансової діяльності підприємств

Змінні моделей по Херсонському нафтопереробному заводу

Х₁ - прибуток ( валовий прибуток, валовий дохід від виробничої діяльності )

Х₂ – інші фінансові доходи

Х₃ – фактичні витрати

Х₄ – фінансові операції від звичайної діяльності

Х₅ – нарахування на прибуток інші операційні доходи

Х₆ – чистий прибуток

Х₇ – адміністративні витрати

Виробничі функції зв’язку факторів взаємовпливу для Херсонського нафтопереробного заводу

Y= - 17300 –5,55X₁+27,89X₂+46,32X₃-129,94X₄+182,08X₅+105,5X₆

Y= 8279,46+0,156X₇+4,60X₂+3,0X₃+0,16X₄+5,60X₅+1,10X₆

Y=-1807,6-0,54X₁+0,06X₇+5,00X₂-0,14X₃+2,01X₄-2,90X₅

Y=- 6899,6-0,42X₆-0,13X₁-0,02X₇+2,98X₃+0,60X₄+1,41X₅

Змінні моделей по НПК-Галичина

Х₁ - прибуток ( валовий прибуток, валовий дохід від виробничої діяльності )

Х₂ – інші фінансові доходи

Х₃ – фактичні витрати

Х₄ – фінансові операції від звичайної діяльності

Х₅ – нарахування на прибуток інші операційні доходи

Х₆ – чистий прибуток

Х₇ – адміністративні витрати

НПК "Галичина"

Y= -206648+4,44X₁+21,3X₂+19,8X₃+1,17X₄-32,5X₅+4,6X₆

Y= 73356,0-0,026X₇-0,87X₂-0,36X₃-0,2X₄+7,94X₅-2,0X₆

Y= 43256,5-1,66X₁+0,04X₇-5,92X₂-0,28X₃+0,67X₄+5,3X₅

Y= 11794,9-0,33X₆-0,31X₁+0,05X₇-1,29X₂+0,03X₄+1,70X₅

Змінні моделей по НПЗ "Нафтохімік Прикарпаття"

Х₁ - виручка від реалізації валовий дохід від виробничої діяльності

Х₂ – чистий доход

Х₃ – чистий прибуток собівартість продукції

Х₄ – заборгованість по кредитам валовий прибуток

Х₅ – заборгованість дебіторська нші операційні доходи

Х₆ – результат від операційної діяльності

Х₇ – результат від іншої операційної діяльності

Х₈ – результат звичайної діяльності

Виробничі функції взаємовпливу показників фінансової діяльності для НПЗ "Нафтохімік Прикарпаття"

Y= 478206 – 0,04X₂+ 31,0X₃ –0,06X₄-2,27X₅+11,74X₆+37,0X₇-36,5X₈

Y= 399556,3-2,03X₁+61,6X₃+14,2X₄-10,0X₅+13,7X₆+57,8X₇-35,7X₈

Y = -3437667,0+5,44X₂+5,37X₁+7,5X₄+9,13X₅-122,9X₆-211,55X₇+167,X₈

Змінні моделей по НПЗ "Лукойл – Одеський нафтопереробний завод"

Х₁ - виручка від реалізації валовий дохід від виробничої діяльності

Х₂ – чистий доход

Х₃ – чистий прибуток собівартість продукції

Х₄ – заборгованість по кредитам валовий прибуток

Х₅ – заборгованість дебіторська нші операційні доходи

Х₆ – результат від операційної діяльності

Х₇ – результат від іншої операційної діяльності

Х₈ – результат звичайної діяльності

Моделі по НПЗ "Лукойл"

Y=-113986-4,5X₂-56,9X₃+59,3X₄-1,84X₅+55,7X₆+138,9X₇-14,0X₈

Y =-32773,8-0,74X₁+8,5X₃+29,07X₄+0,85X₅-9,9X₆-26,37X₇+1,98X₈

Y=-24166,2+0,11X₂+0,14X₁-3,35X₄+0,24X₅+0,11X₆-4,75X₇+1,12X₈

В нашому випадку доречним буде зауважити, що наведені моделі хоча і дозволяють враховувати всю множину факторів, які брали участь в аналізі, однак в цьому немає сенсу. Зовнішні характеристики наведених нами множинних моделей вказують на досить істотний рівень мультікореліантності, тобто в моделях є не коректні зв’язки. Тому відбір факторів доцільно проводити на підставі якісного теоретико-економічного аналізу. За звичай процес реалізується у дві стадії.

-  фактори підбираються виходячи з суті проблеми;

-  вибір відбувається на підставі матриці показників кореляції.

Коефіцієнт інтеркореляції дозволяє виключити з моделі дублюючи фактори. Вважається, що змінні суто колінеарні, якщо . Оскільки, однією з умов побудови рівнянь множинної регресії є незалежність дій факторів (R_xi,xj=0) колінеарність факторів порушує ці умови. Тобто, якщо фактори колінеарні, то один з них можна виключити з аналізу. За звичай переваги віддаються фактору, який при наяві тісного зв’язку з результатом має найменші зв’язки з іншими.

З найбільшими труднощами ми зіткнулись у ситуаціях, коли більш ніж два фактори були пов’язані між собою лінійною залежністю (наявність мультіколінеарності). В цьому випадку варіація вхідних даних не є цілком незалежна і коректно оцінити вплив кожного фактору окремо неможливо.

Дослідники цих процесів для оцінки мультіколеніарності використовують визначальник матриці парних коефіцієнтів кореляції між факторами. В цьому сенсі розроблені нами матриці є дуже важливими. Підкреслимо, що мультіколеніарність згладжується на підставі математичного аналізу суті самих моделей. Оскільки дослідження моделей це інший аспект проблеми, який не пов’язан з задачею, яку ми вирішуємо, тобто ми не ставили за мету дослідити процедурні питання створення багато параметричних моделей, тому свідомо зважуючи на наявність мультіколеніарності у наведених моделях визначимо лише основні фактори сумісної дії на результати прибутковості, спираючись лише на поверхневий коментар одержаних моделей.

Так, на прибуток і чистий прибуток для ВАТ "Херсонський нафтопереробний завод" в найбільшій мірі впливали валовий дохід, відрахування, нарахування і валовий прибуток; на ВАТ " Галичина" – валовий прибуток, нарахування на прибуток і інші відрахування; на ВАТ "Прикарпаття" – результати операційної діяльності, результат від іншої операційної діяльності, виручка; на ВАТ "Лукойл" – заборгованість по кредитах, виручка і результату від іншої операційної діяльності.

Тобто, практично на всіх підприємствах, які ми досліджували, прибуток формувався на підставі впливу майже однакових факторів. Різницю в тенденціях становила ступінь впливу кожного з зазначених факторів. Але це справа більш детального спеціального аналізу з підключення раніше оговорених математичних процедур.