Навигация
Изменение параметров линейной части системы
3. Изменение параметров линейной части системы.
3.1. Уменьшение электромеханической постоянной времени ![]() .
.
3.2. Введение внутренней обратной связи.
Применяя соответствующие обратные связи, можно изменять параметры линейной части системы, а следовательно, и частоту возможных автоколебаний.
Линеаризация.
Релейный элемент является существенно нелинейным элементом. Выходная величина релейного элемента (управляющее воздействие) изменяется скачком, когда входная величина (управляющий сигнал) проходит пороговые значения. В интервале между моментами времени, соответствующими прохождению входной величиной пороговых значений, выходная величина релейного элемента неизменна.
Такие свойства релейного элемента позволяют сравнительно простыми средствами коммутировать большие мощности, но пропорциональность между выходной и входной величинами здесь отсутствует.
Если одновременно с управляющим сигналом на вход релейного элемента подавать дополнительное периодическое воздействие, то релейный элемент может при определенных условиях приобрести свойства пропорциональности. При этих условиях релейный элемент эквивалентен линейному усилителю. Характерной особенностью такого усилителя является зависимость коэффициента усиления от «амплитуды» внешнего воздействия А. Увеличение последней уменьшает коэффициент усиления. Если в релейной системе создать высокочастотные (по сравнению с внешним воздействием) колебания, то релейная система приобретает свойства линейной или пропорциональной системы, причем настройка этой последней системы может осуществляться за счет изменения «амплитуды» этих относительно высокочастотных колебаний. Роль фильтра в релейной системе будет играть ее линейная часть.
Дополнительное высокочастотное воздействие, осуществляющее линеаризацию релейной системы, может быть создано при помощи вынужденных колебаний или автоколебаний, если эти колебания существуют и устойчивы [2].
Процесс линеаризации аналогичен процессу модуляции. Релейный элемент представляет собой модулятор, дополнительное периодическое воздействие соответствует несущей частоте, а внешнее воздействие (управляющий сигнал) — модулирующему сигналу.
Более точно в релейном элементе при наличии дополнительного периодического воздействия происходит своеобразная широтно-импульсная модуляция. Отсюда вытекает соотношение между частотой модулирующего сигнала и несущей, при которой процесс модуляции будет осуществлен без существенных искажений. Отношение частоты несущей к частоте сигнала должно быть по крайней мере больше трех[2]. Это накладывает ограничения на скорость изменения управляющего сигнала.
Линеаризация автоколебаниями.
В качестве дополнительного периодического воздействия, производящего линеаризацию релейной системы, могут быть использованы автоколебания самой релейной системы, если частота их такова, что внешнее воздействие по сравнению с ними можно считать медленно изменяющимся.
Так как обычно частота автоколебаний относительно низка, то для осуществления линеаризации необходимо применять способы повышения этой частоты автоколебаний.
В таблице № 2 приведены некоторые передаточные функции ускоряющих элементов и их характеристики.
Таблица № 2.
| № |
| Выражение годографа | Вид годографа |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
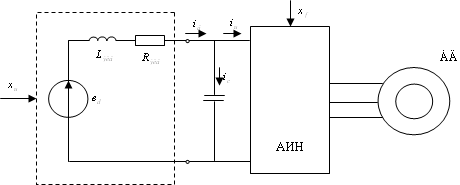
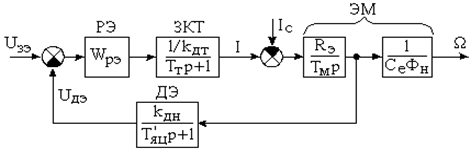
Выделим из структурной схемы электропривода с синхронной машиной, включенной по схеме вентильного двигателя, контур тока (рис. 4.1).
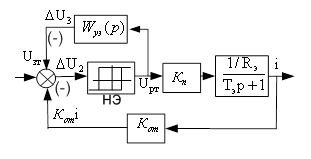
Рис. 4.1
Передаточная функция линейной части системы ![]() , причем степень числителя не больше степени знаменателя.
, причем степень числителя не больше степени знаменателя.
![]() ,
, ![]() (4.0)
(4.0)
Выражение для частотной характеристики разомкнутой релейной системы без зоны нечувствительности имеет вид:
![]() . (4.1)
. (4.1)
Физический смысл выражения (4.1) состоит в том, что результирующая частотная характеристика представляется в виде суммы простейших характеристик, кратных нечетным частотам. Это вытекает из того, что выходной сигнал релейного элемента, имеющий прямоугольную форму, раскладывается в бесконечную сумму ряда Фурье с нечетными гармониками (рис. 4.2.).

Рис. 4.2
Нечетность прямоугольных колебаний относительно начала работы релейного элемента определяет нечетность гармоник.
![]() - частотная характеристика релейной автоматической системы.
- частотная характеристика релейной автоматической системы.
![]() - частотная характеристика системы без ускоряющего элемента.
- частотная характеристика системы без ускоряющего элемента.
![]() - частотная характеристика системы с ускоряющим элементом.
- частотная характеристика системы с ускоряющим элементом.
![]() (4.2)
(4.2)
Характеристика релейной системы ![]() может быть определена по частотной или временным характеристикам или в некоторых случаях по передаточной функции линейной части системы.
может быть определена по частотной или временным характеристикам или в некоторых случаях по передаточной функции линейной части системы.
В дальнейших расчетах будем пользоваться последним методом.
Согласно [2], если передаточная функция такова, что можно найти её полюсы, то характеристика релейной системы ![]() может быть определена через передаточную функцию (точнее через полюсы передаточной функции) не в виде ряда, а замкнутой форме.
может быть определена через передаточную функцию (точнее через полюсы передаточной функции) не в виде ряда, а замкнутой форме.
При действительных отрицательных, не кратных и ненулевых полюсах передаточной функции ![]() справедливо равенство:
справедливо равенство:
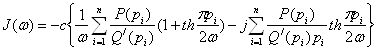 , (4.3)
, (4.3)
где ![]() - полюсы передаточной функции линейной части системы.
- полюсы передаточной функции линейной части системы.
![]() - число полюсов передаточной функции линейной части.
- число полюсов передаточной функции линейной части.
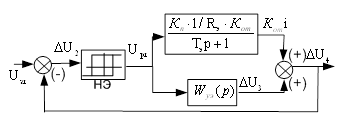
Рис. 4.3
Запишем передаточную функцию линейной части системы без ускоряющего элемента:
![]() (4.4)
(4.4)
![]()
Согласно выражению (4.4), передаточная функция имеет всего один полюс ![]() .
.
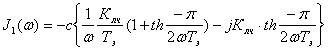 (4.5)
(4.5)
![]() (4.6)
(4.6)
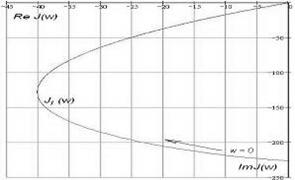
Рис. 4.4.
В качестве ускоряющего элемента, повышающего частоту автоколебаний в системе, примем ![]() . Выражение годографа УЭ согласно таблице № 2 имеет вид:
. Выражение годографа УЭ согласно таблице № 2 имеет вид:
![]() , (4.7)
, (4.7)
где ![]() .
.
Учитывая рекомендации [2], назначим параметры ускоряющего элемента:
![]()
![]()
![]() (4.8)
(4.8)
На рис. 4.5 представлен годограф ускоряющего элемента ![]() , а также результирующий годограф линейной части контура тока
, а также результирующий годограф линейной части контура тока ![]() .
.
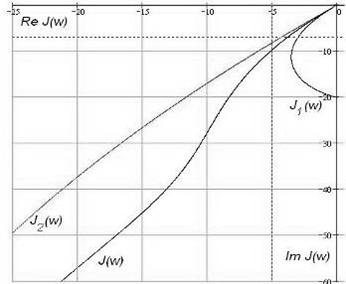
Рис. 4.5
Анализируя поведение годографов на рис. 4.5 можно сделать вывод, что постоянная времени ускоряющего элемента ![]() снижает результирующий годограф линейной части и его точку пересечения с прямой –b. Уменьшение
снижает результирующий годограф линейной части и его точку пересечения с прямой –b. Уменьшение ![]() способствует увеличению автоколебаний системы.
способствует увеличению автоколебаний системы.
Следует отметить, что увеличение коэффициента передачи ускоряющего элемента также увеличивает частоту автоколебаний, одновременно смещая фазу выходного сигнала в сторону отставания. Результирующий коэффициент передачи линейной части контура тока при этом уменьшается.
На рис. 4.6 приведена структурная схема линеаризованного контура тока. Для сравнения на осциллограф выведены сигналы контура тока без линеаризации (рис. 4.7).
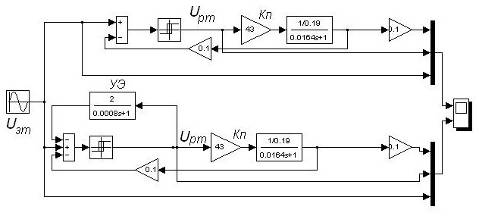
Рис. 4.6
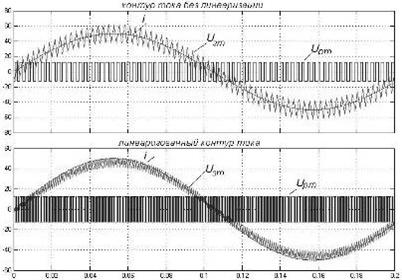
Рис. 4.7
Линеаризовав контур тока, мы получили возможность замены релейного регулятора его коэффициентом передачи ![]() .
.
Рассмотрим контур тока, представленный на рис. 4.8:
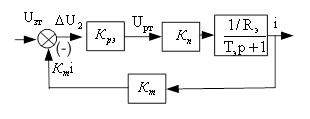
Рис. 4.8
Структурная схема контура тока включает:
Крэ – коэффициент передачи релейного элемента, Кп - коэффициент передачи преобразователя, Rэ - эквивалентное сопротивление цепи статора,
Tэ - электромагнитная постоянная времени статорной цепи.
Передаточная функция замкнутого контура тока имеет вид:
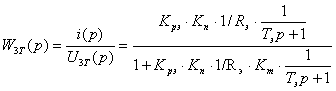 , или
, или
![]() . (4.9)
. (4.9)
Приведем ее к стандартному виду:
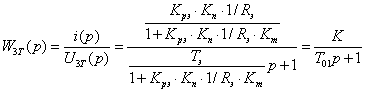 , (4.10)
, (4.10)
где
К- эквивалентный коэффициент усиления замкнутого контура тока,
Т01- эквивалентная постоянная времени замкнутого контура тока.
![]()
![]() (4.11)
(4.11)
![]() (4.12)
(4.12)
Постоянная времени Т01 выбирается исходя из динамических свойств самого реле.
Назначают ![]() , однако очень малое значение постоянной времени практически не влияет на динамические свойства системы.
, однако очень малое значение постоянной времени практически не влияет на динамические свойства системы.
Примем ![]() , тогда замкнутый контур тока можно представить безынерционным звеном с коэффициентом передачи
, тогда замкнутый контур тока можно представить безынерционным звеном с коэффициентом передачи ![]() .
.
5. Синтез контура скорости
На рис. 5.1 приведена структурная схема контура скорости.
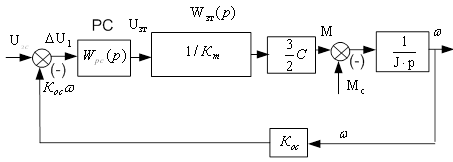
Рис. 5.1
Все передаточные функции (ПФ) контура скорости разобьем на 2 части: ПФ регулятора и ПФ объекта.
Под объектом будем понимать все звенья, исключая регулятор:
![]() . (5.0)
. (5.0)
![]() , (5.1)
, (5.1)
где ![]() .
. ![]()
Регулятор скорости (РС) примем пропорционально-интегральным («ПИ»), наш РЭП примет астатический характер.
Зададимся передаточной функцией разомкнутой системы типа «2-1»:
![]() . (5.2)
. (5.2)
Отсюда можно найти в общем виде передаточную функцию РС:
![]() . (5.3)
. (5.3)
Отсюда можно записать:
![]() . (5.4)
. (5.4)
Здесь введено обозначение:
![]() . (5.5)
. (5.5)
Постоянная времени ![]() определяется исходя из максимального быстродействия системы. Обычно принимают
определяется исходя из максимального быстродействия системы. Обычно принимают ![]() , где
, где ![]() частота коммутации силовых ключей. В физических системах частота коммутации ключей ограничивается условиями нагрева и не выходит их диапазона
частота коммутации силовых ключей. В физических системах частота коммутации ключей ограничивается условиями нагрева и не выходит их диапазона ![]() .
.
Примем ![]() , тогда
, тогда ![]() .
.
Зададимся ![]() , тогда
, тогда ![]()
Коэффициент усиления регулятора скорости:
![]() .
.
ЛАЧХ и ЛФЧХ полученные при синтезе системы, приведены на рис. 5.2.
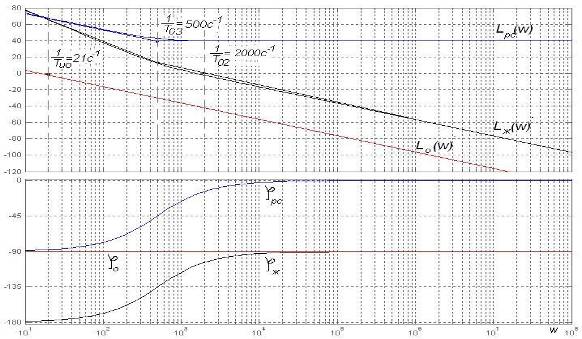
Рис. 5.2
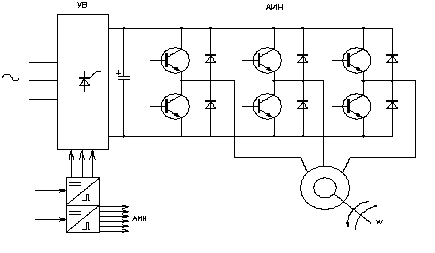
6. Моделирование вентильного двигателя
На рис. 6.1 приведена виртуальная модель РЭП синхронной машины, включенной по схеме вентильного двигателя, составленная в пакете Matlab 6.5.
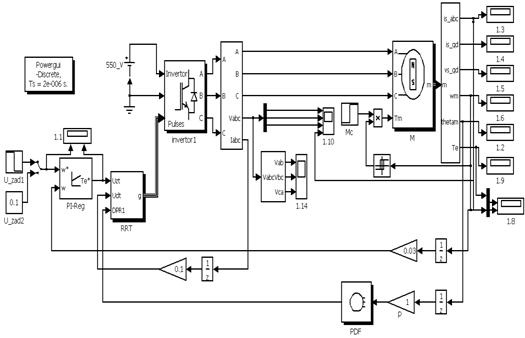
Рис. 6.1
Схема на рис. 6.1 содержит: двигатель трехфазный с постоянными магнитами на роторе (М2), схему управления инвертором (RRT), инвертор напряжения (Invertor1), путевой датчик фазовый ПДФ (PDF).
6.1 Датчик положения ротораРассмотрим структуру схемы по часовой стрелке, начиная с блока ПДФ, представленного на рис.6.2.
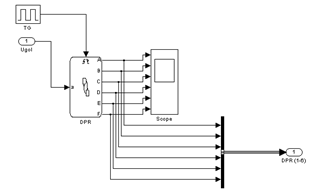
Рис. 6.2
электропривод вентильный двигатель
Входной величиной для ПДФ является угол поворота вала двигателя, а выходным сигналом – вектор из шести единичных импульсов, сдвинутых друг относительно друга на 60 градусов (рис. 6.4). Это дает имитацию шести сигналов от чувствительных элементов, расположенных равномерно вдоль окружности и вырабатывающих импульсы в соответствии с пространственным расположением ротора. Так как ДПР реализован в виде конечного автомата, то для его работы необходим тактовый сигнал, который подается тактового генератора TG. Рассмотрим внутреннюю структуру датчика положения ротора (DPR).
Следует отметить, что ДПР реализован с помощью пакета моделирования Stateflow, который хорошо интегрируется с Simulink и входит в стандартный набор пакетов Matlab.
Пакет Stateflow задуман и предназначен для моделирования сложных систем управления с возможностью ветвления и образованием циклов [18]. Пакет оперирует событиями методом конечных автоматов. Автомат представляет собой звено, осуществляющее преобразование вектора входных переменных XIN в вектор выходных переменных XOUT. В пакете Stateflow автомат представляется в виде графа, в нашем примере граф представлен алгоритмом ДПР [6]. Более подробно о работе пакета Stateflow можно узнать на сайте разработчика Matlab или на русскоязычном форуме Matlab [19]. Достоинством этого способа реализации датчика положения является компактность схемы, простота реализации, прозрачность алгоритма, малая вычислительна нагрузка на ЭВМ. Дополнительное преимущество еще и в том, что алгоритм, реализованный в графе автомата, преобразуется в программный код языка высокого уровня (язык С), что окажется полезным при разработке алгоритма вычисления скорости, дискретного регулятора положения и скорости.
Автомат, представленный на рис. 6.3, имеет 6 состояний (рис. 6.4), в одном из которых автомат находится до тех пор, пока значение входной переменной a (угол поворота) не достигнет значения, при котором произойдет изменение сигналов на выходе датчика. Изменение сигналов на выходе датчика происходит в том случае, когда значение входной переменной a превысит значение величины ![]() или станет меньше значения
или станет меньше значения ![]() .
.
Структурная схема RRT представлена на рис. 6.5.
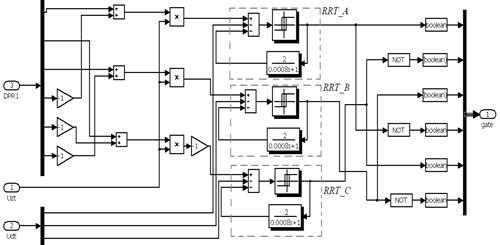
Рис. 6.5
При попытке применить один регулятор тока для всех трех фаз не привели к желаемым результатам, поэтому для каждой фазы принят свой регулятор. Векторный сигнал с датчика положения расщепляется на 6 компонентов, которые образуют разрешающие «единичные» сигналы для переключения ключей инвертора в соответствии с диаграммой работы коммутатора (рис. 6.6).
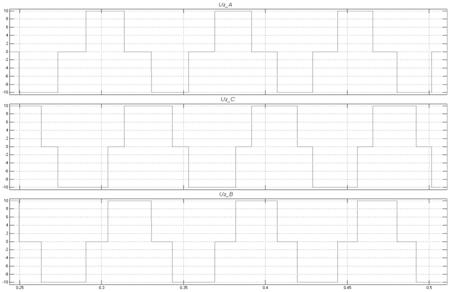
Рис. 6.6
Диаграмма переключения ключей инвертора соответствует алгоритму коммутации коллектора двигателя постоянного тока.
Разрешающие сигналы переключения ключей умножаются с напряжением задания тока и поступают на один из входов релейного регулятора. На второй вход поступают токи обратной связи.
6.3 Инвертор напряженияНа рис. 6.7 представлена структурная схема и нумерация ключей инвертора напряжения.
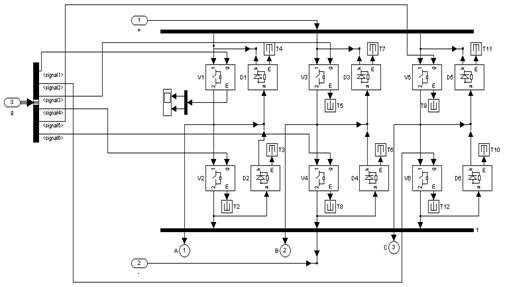
Рис. 6.7
В тиристорном ЭП по трехфазной мостовой схеме выпрямления переключение тиристоров при питании от сети 50 Гц происходит с угловой частотой![]() .
.
В транзисторных ЭП средняя частота переключений обычно находится в пределах![]() , при этом рабочая полоса пропускания частот в два раза ниже. При этом минимальная постоянная времени Т01 может приниматься
, при этом рабочая полоса пропускания частот в два раза ниже. При этом минимальная постоянная времени Т01 может приниматься ![]() . Если частоту коммутации увеличить, то быстродействие также возрастет [8].
. Если частоту коммутации увеличить, то быстродействие также возрастет [8].
На рис. 6.8 представлены фазные напряжения статора двигателя.
Несинусоидальность выходного напряжения приводит к несинусоидальному характеру тока в статорных обмотках и пульсациям момента двигателя. Эти пульсации особенно сильно проявляются при пониженной частоте и небольшом моменте инерции механизма, который приводится в движение приводом. Тогда они вызывают неравномерность вращения, а иногда и возникновение шагового режима, когда двигатель вращается с остановками [14].
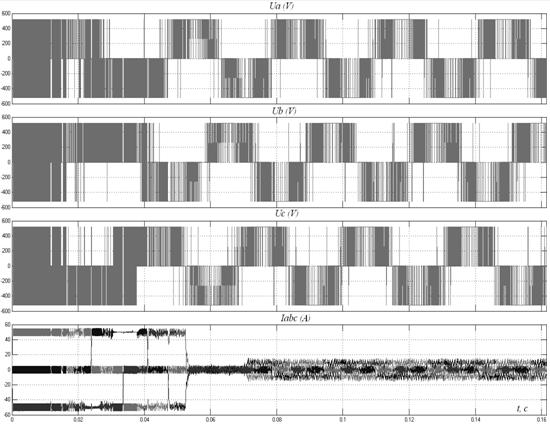
Рис. 6.8
Таким образом, несинусоидальный характер напряжения на выходе выпрямителя накладывает ограничение на возможный диапазон регулирования скорости привода. Кроме того, наличие высших гармоник в кривой тока статора вызывает увеличение потерь энергии по сравнению по сравнению со случаем питания двигателя синусоидальным напряжением.
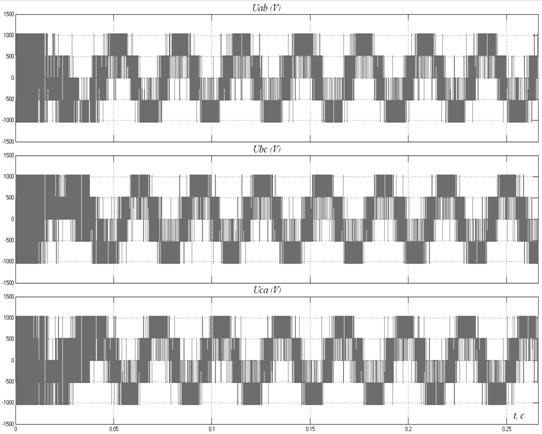
Рис. 6.9
Также для сравнения на рис. 6.9 приведены линейные напряжения статора двигателя.
7. Анализ динамических свойств виртуальной модели вентильного двигателя
Для анализа динамических свойств виртуальной модели вентильного двигателя, кривые скорости ![]() и момента
и момента ![]() сняты на одном экране осциллографа (рис. 7.1).
сняты на одном экране осциллографа (рис. 7.1).
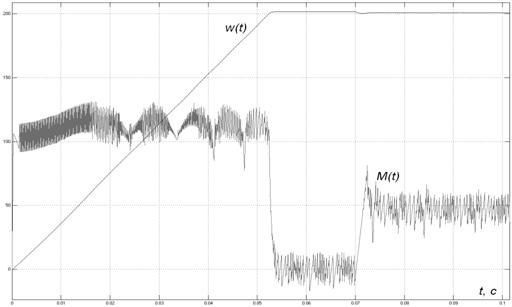
Рис. 7.1
Двигатель разгоняется при максимальном напряжении на номинальную скорость при отсутствии момента сопротивления, потом нагружается моментом, равным ![]() .
.
Из осциллограмм момента и скорости двигателя видно, что момент двигателя не постоянен, и кроме пульсаций, обусловленных работой релейных регуляторов тока, имеет еще и пульсации, аналогичные пульсациям напряжения на выходе трехфазного мостового выпрямителя. Это объясняется тем, что при постоянном токе фазы I момент синхронного двигателя в функции поворота вала ![]() изменяется по синусоиде.
изменяется по синусоиде. ![]() где
где ![]() - коэффициент пропорциональности между током и максимальным значением момента. При
- коэффициент пропорциональности между током и максимальным значением момента. При ![]() , когда ось фазы совпадает с осью q, момент максимальный. Переключение фаз происходит при
, когда ось фазы совпадает с осью q, момент максимальный. Переключение фаз происходит при ![]() и
и ![]() . При этом
. При этом ![]() . Отсюда и соответствующие этому провалы в кривой момента [1]. Такая симметричная относительно максимума форма момента говорит о том, что ДПР настроен правильно. В данной модели подстройка ДПР производится заданием начального угла
. Отсюда и соответствующие этому провалы в кривой момента [1]. Такая симметричная относительно максимума форма момента говорит о том, что ДПР настроен правильно. В данной модели подстройка ДПР производится заданием начального угла ![]() , в реальном электроприводе – поворотом корпуса ДПР относительно корпуса двигателя.
, в реальном электроприводе – поворотом корпуса ДПР относительно корпуса двигателя.
При анализе влияния параметров двигателя на качество переходных процессов следует отметить, что при увеличении числа пар полюсов ![]() уменьшается время разгона скорости до установившегося значения, т.к. увеличение
уменьшается время разгона скорости до установившегося значения, т.к. увеличение ![]() приводит к увеличению электромагнитного момента и динамического ускорения.
приводит к увеличению электромагнитного момента и динамического ускорения.
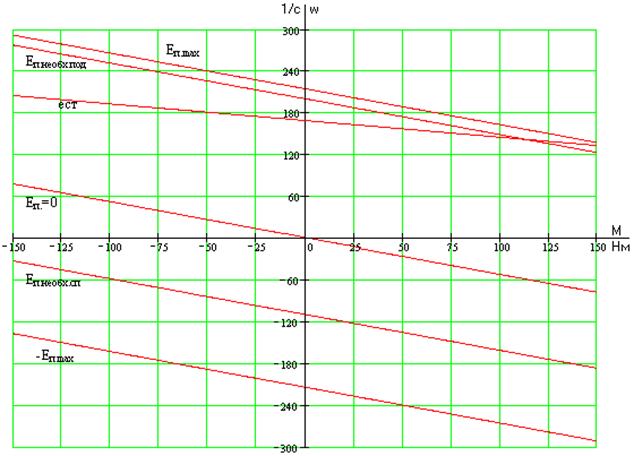
На рис. 7.2. представлена механическая характеристика РЭП на фазовой плоскости, построенная с помощью графопостроителя.
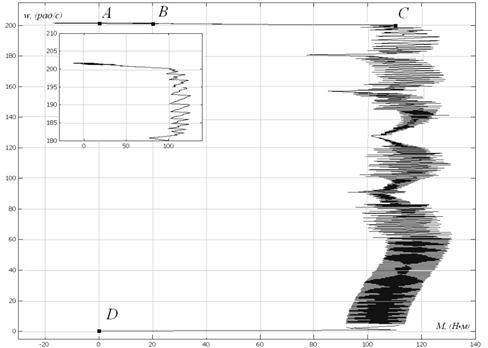
Рис. 7.2
Она получается из временных зависимостей М(t) и w(t) путем исключения из них времени t. При разгоне ЭД годограф вектора электромеханической характеристики проходит последовательно через точки D, C и достигает точки А. Характеристика наглядно показывает динамику разгона двигателя. Также видно, что скорость устанавливается без перерегулирования на уровне расчетного значения.
Чтобы показать астатический характер РЭП, т.е. абсолютную жесткость электромеханической характеристики (неизменность скорости при изменении нагрузки), система была нагружена моментом сопротивления Мс=47, Нм через 0,07с после начала разгона (рис. 7.1). Из-за появления тока, обусловленного нагрузкой, в контуре тока возникает небольшое перерегулирование, что, тем не менее, не сказывается ощутимо на просадке скорости (рис.7.2). Годограф вектора переходит из точки А в точку В.
Очевидно, что точки А, В, С лежат на одном уровне, параллельном оси абсцисс и равном расчетному значению скорости.
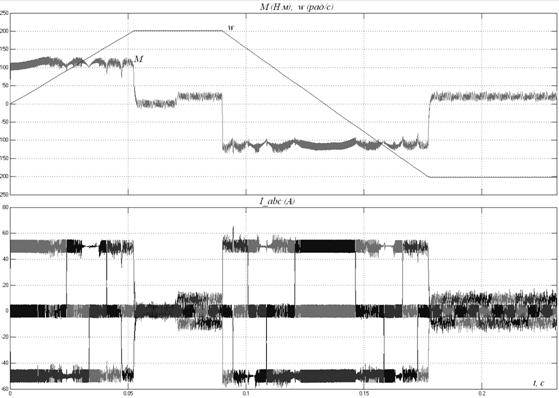
Рис. 7.3
На рис. 7.3 и рис. 7.4 приведены диаграммы реверса вентильного двигателя.
Следует отметить высокое быстродействие регулируемого привода, зависящего от настройки контура скорости. Высокие динамические свойства вентильного двигателя по сравнению ДПТ с тиристорным управлением достигаются за счет использования безынерционного контура тока. Это достигается его линеаризацией, которая проведена с помощью параллельного включения в линейную часть контура ускоряющего элемента (рис. 6.5).
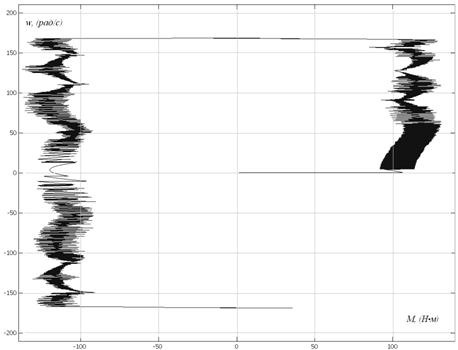
Рис. 7.4
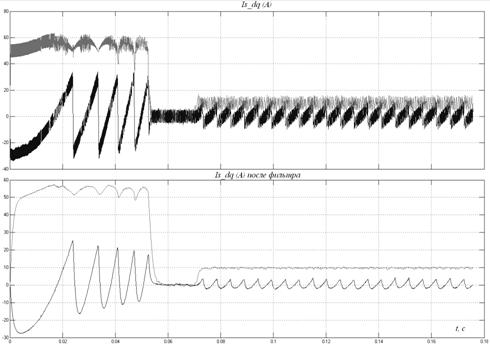
Рис. 7.5
При рассмотрении вентильной машины во вращающейся системе координат ![]() , можно заметить, что при постоянном потоке возбуждения электромагнитный момент двигателя однозначно определяется поперечной составляющей тока
, можно заметить, что при постоянном потоке возбуждения электромагнитный момент двигателя однозначно определяется поперечной составляющей тока ![]() подвижной системы координат (рис. 7.5).
подвижной системы координат (рис. 7.5).
Продольная составляющая тока ![]() не создает полезного момента, вызывает потребление реактивной энергии и с экономической точки зрения вызывает лишь дополнительные потери в виде нагрева двигателя [15]. Наличие реактивного тока связано с эквивалентной постоянной времени статорной цепи
не создает полезного момента, вызывает потребление реактивной энергии и с экономической точки зрения вызывает лишь дополнительные потери в виде нагрева двигателя [15]. Наличие реактивного тока связано с эквивалентной постоянной времени статорной цепи ![]() и перекрестными связями между продольной и поперечной осями двигателя.
и перекрестными связями между продольной и поперечной осями двигателя.
В действительности она больше нуля всегда, что вызывает появление тока ![]() . Устранения потерь добиваются включением в контур реактивного тока
. Устранения потерь добиваются включением в контур реактивного тока ![]() дополнительного регулятора тока [15].
дополнительного регулятора тока [15].
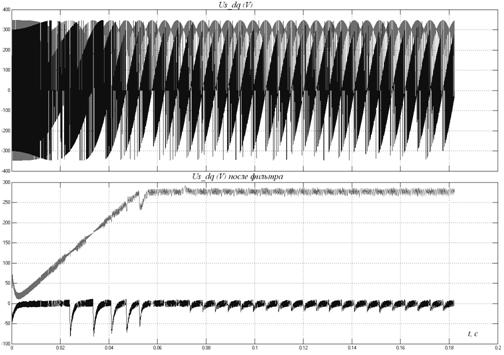
Рис. 7.6
Реактивный ток затрачивается на возбуждение машины (рис. 7.5), который быстро спадает при выходе двигателя на установившуюся скорость. Отметим еще раз, что при появлении нагрузки возникновение реактивного тока неизбежно.
На рис. 7.6 показаны также напряжения статора вентильного двигателя в координатах d,q,0.
На рис. 7.7 изображена диаграмма отработки привода с вентильным двигателем «малого» задания скорости, Uзс=0.01,В.
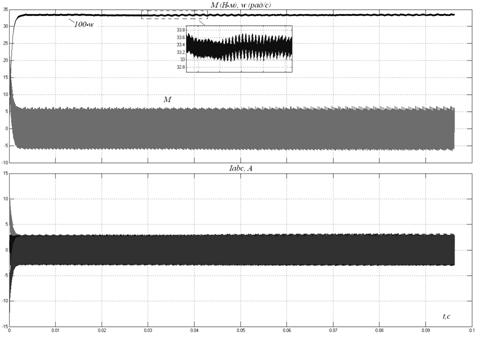
Рис. 7.7
Регулятор скорости не заходит в ограничение. Скорость ротора устанавливается без перерегулирования, ток не достигает своего максимального значения.
Наличие высших гармоник, наложенных на основные измеряемые координаты связано дискретными сигналами управления релейного регулятора тока.
8. Бездатчиковое определение скорости вентильного двигателя
В большинстве приложений, где необходимо получение хороших характеристик электропривода при минимальной его стоимости, наибольший интерес вызывают схемы бездатчикового векторного управления. Прежде всего - это атомная энергетика, в частности, перегрузочные роботы, где необходим более высокий (до 50:1) диапазон регулирования скорости и по условиям технологии исключается возможность установки датчика положения на вал ротора двигателя. К подобным системам управления (СУ) предъявляются также повышенные требования по диапазону регулирования электромагнитного момента - до 10:1.
Применительно к таким схемам термин "бездатчиковое управление" означает отсутствие датчика скорости на валу двигателя, а информация о скорости вращения и потокосцеплениях двигателя извлекается из измеренных токов и напряжений статора. Согласно [3], угловая скорость электрического поля ![]() определяется выражением:
определяется выражением:
![]() (8.0)
(8.0)
где
![]() - потокосцепления статора в неподвижной системе координат.
- потокосцепления статора в неподвижной системе координат.
![]() - число полюсов двигателя.
- число полюсов двигателя.
Структурная схема электропривода с бездатчиковым определением скорости приведена на рис. 8.1.
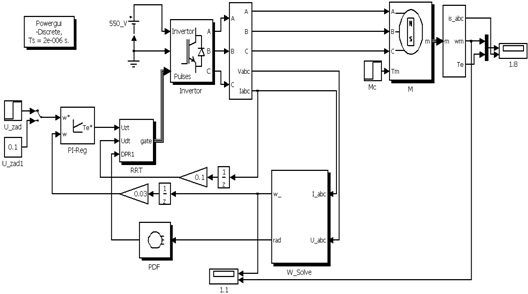
Рис. 8.1
Вычисление скорости производится в блоке W_Solve, изображенной на рис. 8.2.
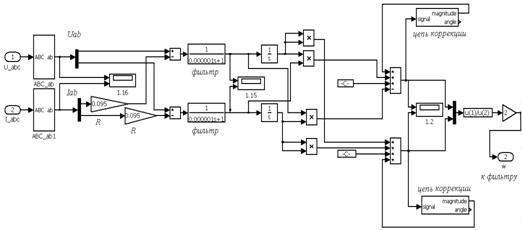
Рис. 8.2
Переход от трёхфазной системы координат к двухфазной и обратно выполняется с помощью формул преобразования координат. Переменные в новой системе координат находятся как сумма проекций в старой системе на оси новой системы координат.
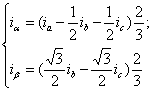 или
или 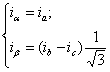 . (8.1)
. (8.1)
Структура преобразователя координат (ABC – ab), собранного по формулам (8.1) приведена на рис.8.3.
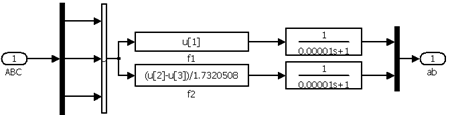
Рис. 8.3
На рис. 8.4 изображены напряжения и токи статора двигателя в неподвижной системе координат после фильтрации высоких частот.
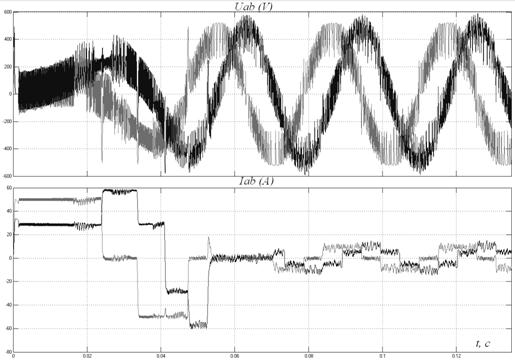
Рис. 8.4
Производные потокосцеплений статора двигателя в неподвижной системе координат приведены на рис. 8.5.
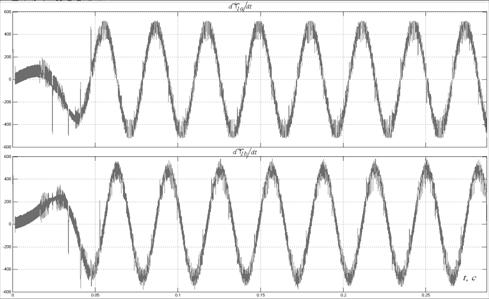
Рис. 8.5
На рис. 8.6 изображены конечные сигналы, участвующие в вычислении скорости, а также скорость двигателя при бездатчиковом определении (рис. 8.7).
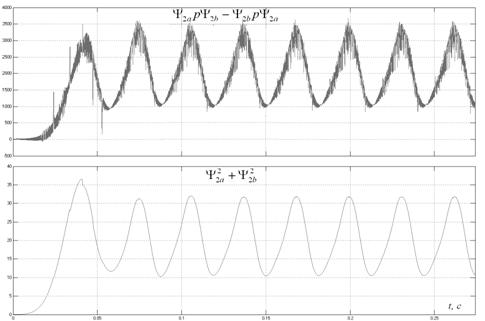
Рис. 8.6
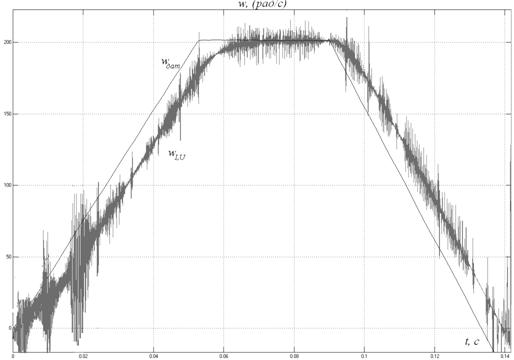
Рис. 8.7
Большинство ведущих мировых производителей электроприводов Siemens, ABB, Schneider Electric, Hitachi, Danhfos и др. поддерживают в своих изделиях все три современные структуры управления ЭД: скалярного, векторного датчикового и векторного бездатчикового. Причем, для последней структуры указывается диапазон регулирования скорости до 50:1. Опыт промышленной эксплуатации таких ЭП в России показывает, что в зоне низких скоростей часто возникают колебания скорости, устранить которые настройками привода не удается и реальный диапазон регулирования скорости заметно ниже [7].
Таким образом, основные проблемы, связанные с построением бездатчикового векторного электропривода заключаются в следующем [17]:
1) Наблюдатель состояния двигателя (ЭД), построенный на основе решения полной системы уравнений электрического равновесия для статора и ротора по доступной информации о напряжениях и токах статора, способен обеспечить приемлемую точность вычисления потокосцепления и скорости только в ограниченном диапазоне частот. Это связано с известной проблемой введения начальных условий при частотах, близких к нулевой. Практически все способы решения данной проблемы связаны с введением определенного отклонения математического описания наблюдателя состояния относительно реального объекта при работе в области малых частот. Эти отклонения проявляются в виде ошибки в вычислении потокосцепления, скорости, активной и реактивной составляющих тока.
2) Следующей проблемой является чувствительность электропривода к изменению его параметров в процессе работы. Прежде всего, это относится к температурным изменениям активных сопротивлений статора и ротора, а также к изменению взаимной индуктивности в зависимости от тока цепи намагничивания. Одним из подходов к решению данной проблемы в построении векторного регулятора и наблюдателя состояния ЭД является применение регуляторов, грубых в отношении параметрических возмущений, в частности, релейных регуляторов, функционирующих в скользящих режимах. Другим подходом является параметрическая адаптация, осуществляемая в реальном времени при работе привода.
3) Третьей проблемой является получение необходимой точности оценки эквивалентных (усредненных на интервале расчета процессов в наблюдателе состояния) значений токов и напряжений статора. На точность оценки эквивалентных напряжений в области малых частот основной гармоники и высоких частот модуляции существенно влияет «мертвое время» и задержки переключения ключей инвертора. Заметим, что проблема точности измерения напряжения на малых частотах в гораздо меньшей степени проявляется в векторных электроприводах с датчиком скорости/положения, так как быстродействующий контур скорости, замкнутый по реально измеряемому сигналу, способен в значительной степени компенсировать ошибки, связанные с динамическими неидеальностями ключей инвертора.
9. Заключение
Сегодня в распоряжении разработчиков появились относительно недорогие редкоземельные магниты из материала неодим-железо-бор с высокими энергетическими характеристиками. Усилиями ученых удалось довести температуру эксплуатации таких магнитов до рабочей температуры механизма, а нанесение коррозионно-стойких покрытий позволило продлить их срок службы на все время работы электропривода.
В настоящее время вентильные двигатели с постоянными магнитами прочно завоевали позицию надежных, компактных и экономичных электромеханических преобразователей энергии. Кроме того, будучи дискретными по своей структуре и имея встроенный датчик положения ротора, они без дополнительных устройств стыкуются с цифровыми блоками управления, что позволяет на их базе легко создавать замкнутые системы электроприводов со сложной циклограммой работы.
Вентильные двигатели с редкоземельными магнитами целесообразно применять не только в медицине и необслуживаемых механизмах, но и в авиационной и космической технике.
10. Список использованной литературы
1. Донской Н.В. Регулируемые электроприводы переменного тока/ - Чебоксары: Изд-во Чуваш. ун-та, 2007. – 204 с.
2. Цыпкин Я. З. Релейные автоматические системы. Главная редакция физико-математической литературы, изд-во «Наука», М., 1974, 576 стр.
3. Соколовский Г.Г. Электроприводы переменного тока с частотным регулированием: учебник для студ. высш. учеб. заведен. М.: Издательский центр «Академия», 2006. – 272с.
4. Анхимюк В., Опейко О.Ф. Проектирование систем автоматического управления электроприводами: Учеб. пособие для вузов.: Мн.: Высш. шк., 1986г – 143 с
5. Башарин А.В., Новиков В.А., Соколовский Г.Г. Управление электроприводами: Учеб. пособие для вузов.: -Л.: Энергоиздат, Ленингр. отд-ие, 1982г – 392 с.
6. Туренко Т.В. Применение пакетов SIMULINK И STATEFLOW для моделирования гибридной системы прямого цифрового управления унитарно-кодовым датчиком СПБГУ "ЛЭТИ", г. Санкт-Петербург. –
Труды Всероссийской научной конференции «Проектирование научных и инженерных приложений в среде MATLAB» Часть 5. Имитационное моделирование. Simulink и Stateflow под общ. ред. И.В. Черных.
7. Корельский Д.В., Потапенко Е.М., Васильева Е.В. Обзор современных методов управления синхронными двигателями с постоянными магнитами// Науковий журнал "Радiоелектронiка. Iнформатика. Управлiння", 2001. - с. 155-159.
8. Панкратов В.В. Тенденции развития общепромышленных электроприводов переменного тока на основе современных устройств силовой электроники// Силовая интеллектуальная электроника. Специализированный информационно-аналитический журнал. 2005, №2, с. 27-31
9. Joachim Holtz. Sensorless Control of Induction Motor Drive. - Fellow, IEEE, Vol .90, No.8, Aug.2002 – Germany.
10. Kim Gauen and Jade Alberkrack. Three Piece Solution for Brushless Motor Controller Design. July, 2005− Rev. 5
11. J. P. Johnson, M. Ehsani, and Y. Guzelgunler. "Review of sensorless methods for brushless DC," presented at 1999 IEEE Industry Applications Conference, 1999.
12. P. P. Acarnley and J. F. Watson. "Review of position-sensorless operation of brushless permanent-magnet machines," IEEE Transactions on Industrial Electronics, vol. 53, pp. 352-362, Apr. 2006.
13. SimPowerSystemsTM Release Notes.
14. Binns K.J.; Sneyers B.; Maggetto G.; Lataire Ph. Rotor-position-controlled permanent magnet synchronous machines for electrical vehicles, ICEM ‘80, 1980, pp. 346-357.
15. Slemon, G. R.; Xian, L. Modelling and Design Optimisation of Permanent Magnet Motors, Electric Machines and Power Systems, vol. 20, no. 2, 1992, pp. 71-92.
16. Zhong L.; Rahman M.F.; Lim K.W. Modelling and experimental studies of an instantaneous torque and field weakening control scheme for an interior permanent magnet synchronous motor drive, ELECTRIMACS 1996, pp. 297-302.
17. А.Б. Виноградов, И.Ю. Колодин, А.Н. Сибирцев. Адаптивно-векторная система управления бездатчикового асинхронного электропривода серии ЭПВ. – статья. http://www.vectorgroup.ru/articles/article12
Дополнительные источники информации
18. www.elprivod.ru
19. www.exponenta.ru
[1] ЗАО « Электротехнические системы», Санкт – Петербург.
[2] Согласно теореме Котельникова
Похожие работы
... равное отношению угловой частоты ЭДС ротора Ω2 (приведенной к двухполюсному электродвигателю) к номинальному значению угловой частоты напряжения статора Ω1н. . Структурная схема асинхронного электродвигателя при управлении напряжением статора показана на рис. 2. Рис.2. 2.3 Статические характеристики САУ на основе АД 2.3.1 Статические характеристики САУ при Для ...
... от переподъемов, нулевую и максимальную защиты. - предусматривать остановку сосудов в промежуточных точках ствола. световую сигнализацию о режимах работы подъемной установки в здании подъемной машины, у оператора загрузочного устройства, у диспетчера. Современные регулируемые электроприводы постоянного тока для автоматизированных подъемных установок выполняют на основе двигателей постоянного ...
ерсивного тиристорного электропривода постоянного тока с обратной связью по ЭДС и стабилизацией тока возбуждения двигателя. Данный электропривод постоянного тока разрабатывается на основе комплектного тиристорного электропривода ЭПУ. Применение тиристорного электропривода позволяет оптимизировать его работу на отработку необходимых технологических операций. В данной курсовой работе необходимо ...
... обмоток трансформатора: Ом Rуд – активное сопротивление уравнительных дросселей: Ом. Итак, Ом Ом. Выводы по главе 1. В главе 1 на основе технических данных и требований электропривода подъемного механизма крана был произведен выбор схемы ЭП. В результате анализа и обзора применяемых систем регулирования показана целесообразность применения системы тиристорный преобразователь – ...
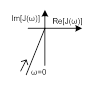
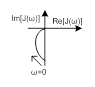
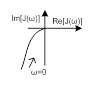
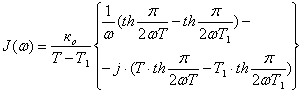
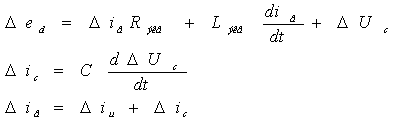
0 комментариев