Навигация
Изучение работы и снятие характеристик импульсного оптического квантового генератора
6. Изучение работы и снятие характеристик импульсного оптического квантового генератора
преломление оптический свет квантовый
Оптическими квантовыми генераторами (ОКГ) на твердом теле называются такие приборы, в которых в качестве активной управляющей среды используется кристаллический или аморфный диэлектрик. Примерами твердотельных ОКГ могут служить широкоизвестные рубиновые ОКГ или генераторы на стекле, активированные неодимом. Для них инверсия населенности образуется на энергетических уровнях атомов и ионов вещества, находящегося в твердом агрегатном состоянии. Причем концентрация активных частиц в твердом материале на несколько порядков превышает концентрацию активных частиц в газовых средах. Поэтому в твердом теле абсолютная величина инверсии населенности может быт существенно больше, чем в газах. Отсюда понятно, что твердые активные среды должны характеризоваться высоким коэффициентом усиления. Это в свою очередь позволяет получать большие мощности генерации и добиваться генерации при малой длине активного элемента.
Твердое тело как оптическая среда обладает гораздо меньшей оптической однородностью по сравнению с газами. Это приводит к возникновению объемных потерь на рассеяние, снижению добротности резонатора при значительной длине активного элемента. Поэтому активные элементы твердотельных ОКГ имеют длину не более 50-60 см. для наиболее оптически однородных материалов. Оптическая неоднородность среды приводит к тому, что сверхпороговая инверсия создается не по всему сечению активного элемента, а в определенных узких каналах. Поэтому угол расхождения пучка генерируемого излучения, оцениваемый даже из дифракционных соображений, оказывается значительным.
В твердом теле взаимодействие между частицами существенно искажает структуру энергетических уровней. Так для спонтанного излучения характерна ширина полосы в несколько ангстрем. Ширина линии генерации в лучшем случае составляет доли ангстрем.
Способ создания инверсии в твердотельных ОКГ принципиально отличается от накачки газовых лазеров. Он не может быть связан с прохождением электрического тока через твердый диэлектрик. Для них характерна оптическая накачка, при которой заселение возбужденных состояний достигается путем интенсивного облучения активного элемента излучением внешнего источника. Специально подобранный спектральный состав этого излучения или определенное соотношение между вероятностями соответствующих переходов приводит к преимущественному заселению верхнего рабочего уровня и возникновению инверсии.
Действие ОКГ на твердых телах основано на тех же квантовомеханических принципах, что и газовые лазеры. Поэтому, здесь, основные математические выкладки, показывающие условия генерации в твердотельных ОКГ, не приводятся (смотрите лабораторную работу №6 "Изучение работы и снятие характеристик газового лазера").
Цель лабораторной работы - ознакомить студентов с принципом работы твердотельных ОКГ и свойствами его излучения, на основе активного элемента рубина.
I. Рубин как активная среда для импульсных ОКГ.
Рубин - кристаллический минерал, имеющий окраску от бледно-розового до ярко-красной. Структурой рубина является кристаллическая решетка Al2O3 с внедренными в нее трехзарядными ионами хрома Cr3+. Содержание хрома колеблется обычно в пределах от 0.05 до 0.5 %. Цвет кристалла определяется содержанием хрома - чем больше хрома, тем более красный оттенок имеет рубин. Рубин обладает очень большой твердостью, а также хорошей теплопроводностью, что способствует быстрому охлаждению рубинового стержня. Он вырезается в виде цилиндрического стержня, торцы которого шлифуются до параллельности.
Активный элемент - рубин ОКГ должен удовлетворять следующим требованиям:
* допускать активировку элементами, на которых осуществляется генерация;
* быть химически стойким и механически прочным, чтобы обеспечить долговечность среды;
* выдержать значительные нагревы, которые возможны при высокой плотности излучения оптической накачки и генерации;
* технология должна быть доступна для массового производства;
* быть прозрачным для излучения накачки и генерации;
* быть оптически однородным, так как рассеяние на неоднородностях среды вносит дополнительные потери и снижает добротность резонатора.
Электронная конфигурация основного состояния трехзарядного иона хрома-3.
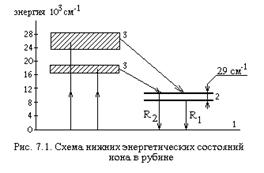
Вследствие взаимодействий между ионами кристаллической решетки основное состояние расщеплено на ряд уровней. Схема нижних энергетических уровней приведена на рис. 7.1. Два близко расположенных уровня 2 - метастабильные долгоживущие состояния. Время жизни данного состояния в квантовой механике определяется суммой вероятностей всех спонтанных переходов в низшие состояния 1
![]()
где t2 - характеризует время, в течение которого населенность состояния уменьшается в е раз.
Ширина энергетического уровня DW2 связана со временем жизни данного состояния соотношением:
DW2 = h/t2,
где h – постоянная Планка.
Таким образом, чем больше время жизни данного состояния, тем меньше ширина его энергетического уровня.
Переход 2 ® 1 в трехзарядном ионе Cr3+ запрещен правилом отбора. Два широких уровня 3 соответствуют состояниям с малым временем жизни, причем наиболее вероятен спонтанный переход 3 ® 2. Этот переход безизлучательный - избыток внутренней энергии иона переходит в тепловую энергию кристаллической решетки.
Инверсное заселение состояний происходит по трехуровневой схеме.
Излучение накачки поглощается в кристалле на переходах 1 ® 3.
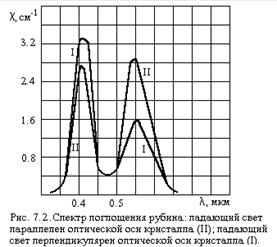
Спектр поглощения рубина соответствует раздвоенной структуре состояния 3. Он содержит две широкие (Dl»1000![]() ) полосы поглощения, максимумы которых приходятся на зеленую и фиолетовую области спектра. Спектр поглощения рубина представлен на рис. 7.2, где две зависимости соответствуют двум ориентациям падающего излучения относительно оптической оси кристалла. В результате поглощения излучения накачки ионы хрома переходят в одно из состояний 3. Затем за счет спонтанного безизлучательного распада этих состояний ионы оказываются в метастабильных состояниях 2. Поскольку в данном случае выполняется условие
) полосы поглощения, максимумы которых приходятся на зеленую и фиолетовую области спектра. Спектр поглощения рубина представлен на рис. 7.2, где две зависимости соответствуют двум ориентациям падающего излучения относительно оптической оси кристалла. В результате поглощения излучения накачки ионы хрома переходят в одно из состояний 3. Затем за счет спонтанного безизлучательного распада этих состояний ионы оказываются в метастабильных состояниях 2. Поскольку в данном случае выполняется условие ![]() населенность состояния 2 при соответствующей плотности накачки может превысить населенность невозбужденного состояния и на переходах 2 ® 1 возникает генерация. В рубиновом ОКГ генерация осуществляется на двух линиях, которые обычно обозначают R1 и R2. Длина волны этих линий зависит от температуры кристалла, так как температура изменяет характер внутрирешеточного расщепления основного ионного состояния. Зависимость длины волны генерации от температуры кристалла является специфической особенностью твердотельных ОКГ. Значение длины волны генерации на рубине при комнатной и азотной температурах приведены в таблице 7.1.
населенность состояния 2 при соответствующей плотности накачки может превысить населенность невозбужденного состояния и на переходах 2 ® 1 возникает генерация. В рубиновом ОКГ генерация осуществляется на двух линиях, которые обычно обозначают R1 и R2. Длина волны этих линий зависит от температуры кристалла, так как температура изменяет характер внутрирешеточного расщепления основного ионного состояния. Зависимость длины волны генерации от температуры кристалла является специфической особенностью твердотельных ОКГ. Значение длины волны генерации на рубине при комнатной и азотной температурах приведены в таблице 7.1.
Таблица 7.1
| Линии | l, | |
| T=300oK | T=77oK | |
| R1 | 6943 | 6934 |
| R2 | 6929 | 6929 |
Генерация на рубине в настоящее время реализуется как в импульсном, так и в непрерывном режиме. Для импульсного режима характерны миллисекундные импульсы генерации, в этом случае используются импульсные ксеноновые лампы. Пороговая энергия накачки зависит при выбранной лампе от объема и температуры кристалла, а также от конструкции системы накачки. Стержень и лампа обычно располагаются параллельно друг к другу внутри круглого цилиндрического осветителя, иногда используются эллиптические или же двойные эллиптические отражатели. В практике применяются кристаллы диаметром от (12-15) мм. и длиной (15-20) см. На торцы рубина наносится серебряное или диэлектрическое покрытие, так, чтобы один был полностью, а другой частично отражающим или же отшлифованный рубин помещается внутри открытого резонатора Фабри-Перо. Пороговая энергия для рубина составляет сотни джоулей, а коэффициент полезного действия не превышает 1%.
II. Монохроматичность и когерентность твердотельных ОКГ.
Одной из основных характеристик излучения является ширина его спектра, то есть диапазон частот или длин волн, который занимает излучение. Ширину спектра излучения удобно характеризовать степенью монохроматичности. В случае спектральной линии степень монохроматичности равна:
где ![]() полуширина линии, а
полуширина линии, а ![]() центральная частота.
центральная частота.
Если ![]() то излучение идеально монохроматично. Если
то излучение идеально монохроматично. Если ![]() то излучение называется квазимонохроматическим или почти монохроматическим. Из определения степени монохроматичности следует, что идеально монохроматическое излучение - это излучение, ширина спектра которого равна нулю. Такое излучение можно сопоставить лишь с колебанием электромагнитной энергией, бесконечной продолжительности.
то излучение называется квазимонохроматическим или почти монохроматическим. Из определения степени монохроматичности следует, что идеально монохроматическое излучение - это излучение, ширина спектра которого равна нулю. Такое излучение можно сопоставить лишь с колебанием электромагнитной энергией, бесконечной продолжительности.
В случае, когда излучение занимает протяженный участок спектра, степень монохроматичности определяется логарифмом отношения крайних частот спектра: m = ln(w2/w1) = 2.3 lg(l1/l2).
Современные ОКГ на рубине имеют мощность в импульсе несколько киловатт, а некоторые ОКГ обладают мощностью порядка сотен и тысяч мегаватт при площади сечения пучка 1 см2. Излучение рубиновых ОКГ состоит из нескольких очень узких спектральных линий, шириной примерно 10-4 - 10-3![]() .
.
В оптическом диапазоне излучения лазеров различают временную (разность фаз для двух фиксированных точек вдоль направления луча не зависит от времени или, то же самое, разность фаз измеренная в одной точке пространства в начале и конце фиксированного интервала времени Dt, не изменяется со временем) и пространственную (разность фаз для двух фиксированных точек в плоскости, перпендикулярной к направлению луча, не зависит от времени) когерентности.
При оценке временной когерентности весьма полезно пользоваться понятием длины когерентности источника. Предположим, что источник излучает монохроматический волновой цуг определенной длины l и, что мгновенные значения амплитуды можно одновременно измерить в двух точках z1 и z2, расположенных на одной нормали к волновому фронту. Если разность Dz= z2 - z1 немного меньше чем l, то в течение короткого периода может казаться, что источник обладает временной когерентностью. Интервал Dz=l, для которого сохраняется некоторая степень постоянства разности фаз во времени, есть мера длины когерентности волнового источника. Длину когерентности l можно выразить через произведение l=с×Dt, где Dt- время, в течение которого источник излучает непрерывный цуг. В голографии, как мы увидим, длина когерентности накладывает ограничение на допустимую разность в длине пути опорного и рабочего пучков.
Длину когерентности можно выразить через другие физические величины. Так, например, разложив одночастотный волновой цуг продолжительностью Dt на фурье-компоненты и, учитывая пропорциональность интенсивности света квадрату фурье-образа, можно установить связь длины когерентности с шириной полосы частот Dn
l=c/Dn
Временную когерентность можно также связать с контрастом полос интерференционной картины, то есть со степенью различия освещенности экрана в максимумах и минимумах. Количественной характеристикой контрастности интерференционной картины служит безразмерная величина - видность полос g, которую Майкельсон определил следующим образом:
![]()
Контраст интерференционной картины зависит от размеров и формы источника света.
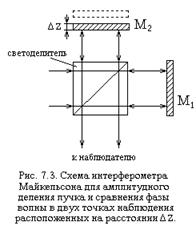
Методы амплитудного деления пучков (например, с помощью интерферометра Майкельсона) позволяют сравнить фазы плоской волны в различных точках вдоль направления распространения рис. 7.3.
Если наклонить одно из зеркал, то сравнение облегчается, поскольку в этом случае плоские волны, выделенные из пучка, пересекаются и образуют систему линейных интерференционных полос, интенсивность которых в плоскости наблюдения дается выражением:
![]()
Более общее выражение для интенсивности, справедливое и для частично когерентного света, можно получить заменяя комплексные амплитуды а1 и а2 комплексными напряженностями электрических полей v1, v2, и добавляя скобки, означающие усреднение по времени. Тогда:
![]()
Следует отметить, что операция усреднения по времени дает разные результаты в случае частичной и в случае абсолютной когерентности. Это проявляется в видности полос. При g=1 видность имеет максимальное значение, равное единице, что соответствует абсолютной когерентности.
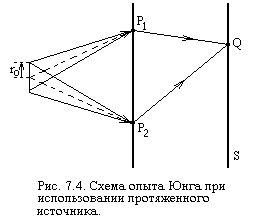
Комплексная степень когерентности h(t), устанавливающая связь между электрическими полями Vp1(t) и Vp2(t) в точках p1 и p2 (как показано на рис. 7.4) и усредненным по времени интерференционным членом в точке Q определяется согласно Борну и Вольфу, как нормированная корреляция между Vp1(t) и Vp2(t):
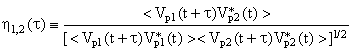 .
.
Связь между h(t) и ![]() устанавливается формулой
устанавливается формулой
![]() ,
,
где J1 и J2 - интенсивности света, приходящих в точку Q из p1 и p2 соответственно, t - разность времени прохождения света в точку Q из точек p1 и p2, b1,2 - фаза величины h1,2(t).
Подставляя эти величины в выражение, определяющее видность полос, получим:
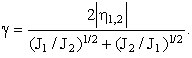
Когда интерферирующие волны имеют равную интенсивность, то видность полос определяется абсолютной величиной степени когерентности.
При t®0 видности полос, полученных в установке с двумя отверстиями (см. рис. 7.4), по существу является мерой пространственной когерентности. Согласно теореме Ван-Циттерта-Цернике степень пространственной когерентности связана с поперечным размером источника посредством преобразования Фурье. Здесь, мы, ограничимся формулировкой этой теоремы. Для протяженного источника, содержащего взаимные некогерентные осцилляторы излучения в узкой спектральной полосе шириной Dn теорема Ван-Циттерта-Цернике читается следующим образом: когда малый источник освещает две близко расположенные точки, лежащие в плоскости, находящейся на большом расстоянии от источника, степень когерентности комплексных электрических полей в этих двух точках дается величиной нормированного Фурье-образа распределения интенсивности источника.
В отличие от обычных источников ОКГ обладают высокой степенью пространственной и временной когерентности.
III. Мощность и направленность твердотельных ОКГ
Излучение, распространяющееся в пределах небольшого телесного угла, называется направленным. Направленный световой пучок должен иметь плоский или почти плоский волновой фронт.
Обычные источники обладают очень низкой направленностью излучения. Диаграмма направленности элементарных излучателей (атомов и молекул), из которых состоит источник, при определенной их ориентации характеризуется телесным углом примерно 2p. Параллельные лучи для этих источников можно получит при установлении диафрагмы на очень большом расстоянии от самого источника. Однако выделенные таким путем параллельные лучи несут небольшую часть энергии излучаемой источником. Почти параллельные лучи обычных источников можно также получить, если поместить источник в фокальной плоскости линзы коллиматора. Если при этом допустить, что источник представляет собой точку, аберрации оптики отсутствуют, то получим параллельный пучок, расходимость которого будет определяться дифракцией на линзе коллиматора. Здесь, как и в первом случае, энергия такого пучка будет ничтожной, так как источник очень малого размера будет излучать чрезвычайно малую энергию. Если же в фокальной плоскости линзы поместит источник конечных размеров, то коллиматор даст пучок с расходимостью равной размеру источника деленному на фокусное расстояние линзы.
Излучение твердотельных ОКГ является когерентным и поэтому фронт волны представляет собой почти плоскость или часть сферы большого радиуса. Расходимость для них определяется дифракцией на выходном отверстии.
Дифракционный угол расхождения лучей из ОКГ определяется соотношением:
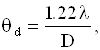
где l - длина волны излучения, D - диаметр излучающей поверхности.
Если в случае обычных источников степень параллельности лучей прямо связывается с энергией излучения, то для ОКГ такой непосредственной связи нет и поэтому почти параллельные лучи могут переносить большую энергию.
Мощность оптического излучения представляет собой энергию, переносимую излучением за единицу времени. Импульсная мощность определяется как отношение величины энергии в импульсе к длительности импульса:
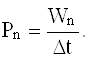
Средняя мощность определяет собой величину
![]()
где Т - период повторения импульсов.
Мощность, отнесенная к единице спектрального интервала, в котором происходит излучение, называется спектральной интенсивностью.
Мощность тепловых источников излучения определяется температурой и является вследствие этого ограниченной. По своей импульсной мощности и спектральной плотности интенсивности мощные ОКГ значительно превосходят все существующие источники излучения в оптическом диапазоне спектра.
ОКГ излучают всю энергию в узком спектральном диапазоне, оно когерентно и распространяется в пределах очень небольшого телесного угла.
Похожие работы
... датчика и осциллографа. Экспериментальные кривые зависимости времени τ горения частиц от давления p, соответствуют теоретической зависимости. Представляют интерес экспериментальные исследования процесса горения отдельной угольной частицы, движущейся в потоке газа. Такого рода опыты проводили Н. И. Сыромятников и 3.И.Леонтьева. После воспламенения частицы наблюдалось замедление скорости ее ...
... пластмасс различного назначения. Приводимый ниже материал предназначен для студентов химического отделения, специализирующихся по органической химии и химии и физике высокомолекулярных соединений, а также может быть полезен аспирантам, инженерам и научным работникам. 2.1 Метод изучения релаксации напряжения Явление релаксации - это процесс перехода из неравновесного в равновесное состояние ...
... к решению соответствующего интегрального уравнения, при этом могут быть использованы численные методы - аналитические зависимости в этом случае получить не удается. Еще сложнее описать процессы испарения и конденсации частиц, в среде, состоящей из нескольких летучих компонентов [23]. Предполагалось, что процесс стационарный, испаряющиеся компоненты химически инертны, пары представляют собой ...
... для анализа и проверки существующих теорий о процессах, протекающих в пламени, а также для развития и построения новых теорий. Таким образом, целью настоящей работы является изучение существующих методик диагностики пламен и их применения для исследования различных характеристик пламен. Феноменология пламени. Процесс горения веществ – эта сложная быстропротекающая экзотермическая реакция ...

0 комментариев