Навигация
Багатоканальні СМО з очікуванням без обмеження на довжину черги
2. Багатоканальні СМО з очікуванням без обмеження на довжину черги
система масове обслуговування очікування черга
Для того, щоб скласти рівняння для перехідних імовірностей у випадку, коли СМО має безліч місць у накопичувачі, треба із системи (14) викреслити останнє рівняння і покласти ![]() . Питання існування фінальних ймовірностей для такої системи пов’язано з умовами, які дають можливість виконуватися рівності
. Питання існування фінальних ймовірностей для такої системи пов’язано з умовами, які дають можливість виконуватися рівності  , а це, якщо врахувати
, а це, якщо врахувати
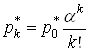 ,
, ![]() ,(22)
,(22)
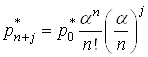 ,
, ![]() (23)
(23)
то (21) дає
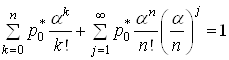 .(24)
.(24)
Другий доданок у (24) є нескінченний ряд, який утворений із геометричної прогресії із знаменником ![]() . Отже, для того, щоб він був збіжний, потрібно, щоб
. Отже, для того, щоб він був збіжний, потрібно, щоб ![]() . Це є умовою, для існування фінальних імовірностей
. Це є умовою, для існування фінальних імовірностей ![]() , коли
, коли ![]() . З точки зору практичного використання цієї умови необхідно, щоб середня кількість заявок, які надходять до системи за середній час обслуговування однієї заявки одним каналом, була строго меншою ніж кількість каналів. Тоді формула (21) спрощується:
. З точки зору практичного використання цієї умови необхідно, щоб середня кількість заявок, які надходять до системи за середній час обслуговування однієї заявки одним каналом, була строго меншою ніж кількість каналів. Тоді формула (21) спрощується:
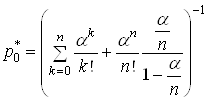 при умові
при умові ![]() (25)
(25)
Основні характеристики СМО з очікуванням. Зупинимось на таких характеристиках СМО з очікуванням, коли довжина черги нескінченна, як середнє число заявок у черзі, середнє число заявок у СМО, функція розподілу часу очікування початку обслуговування, середній час перебування заявки
у СМО.
1. Середнє число заявок у черзі
Оскільки число заявок в черзі є випадковою величиною із значеннями
0, 1, 2, … і ймовірностями відповідно ![]() , тоді середнє число заявок у черзі є математичне сподівання цієї величини, тобто:
, тоді середнє число заявок у черзі є математичне сподівання цієї величини, тобто:
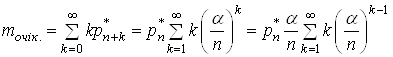 .(26)
.(26)
Для того, щоб знайти суму ряду 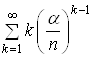 , спочатку знайдемо суму ряду
, спочатку знайдемо суму ряду 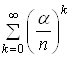 , який утворено від геометричної прогресії із знаменником
, який утворено від геометричної прогресії із знаменником ![]() , тобто
, тобто  . Оскільки останній ряд є степеневий ряд відносно
. Оскільки останній ряд є степеневий ряд відносно ![]() , то він рівномірно збігається для усіх
, то він рівномірно збігається для усіх ![]() , тому його можна почленно диференціювати по
, тому його можна почленно диференціювати по ![]() . Тоді матимемо
. Тоді матимемо
 (27)
(27)
Тепер врахуємо (27) у рівності (26):
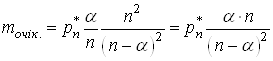 ,(28)
,(28)
де 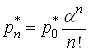 і
і ![]() обчислюється за формулою (25).
обчислюється за формулою (25).
Середнє число заявок у СМО обчислюється:
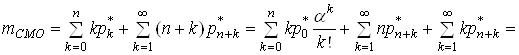
(29)
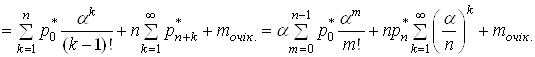 .
.
Оскільки

тоді (29) можна спростити:

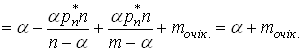 .
.
Таким чином середнє число заявок у СМО є
![]() ,(30)
,(30)
тобто складається із середнього числа заявок, що находять за середній час обслуговування однієї заявки і середнього числа заявок, що очікують у черзі.
3. Функція розподілу часу очікування початку обслуговування
Нехай ![]() є випадкова величина часу, який заявка чекає у СМО до початку обслуговування. Необхідно визначити функцію розподілу цієї величини, тобто
є випадкова величина часу, який заявка чекає у СМО до початку обслуговування. Необхідно визначити функцію розподілу цієї величини, тобто ![]() . Якщо використати визначення функції розподілу, то матимемо:
. Якщо використати визначення функції розподілу, то матимемо:
![]() .
.
Знайдемо ![]() при умові, що час очікування обслуговування
при умові, що час очікування обслуговування ![]() є випадкова подія, коли усі канали вільні, чи коли зайнятий хоча б один з
є випадкова подія, коли усі канали вільні, чи коли зайнятий хоча б один з ![]() каналів, тобто
каналів, тобто

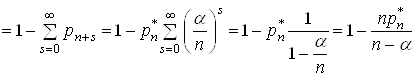 .
.
Таким чином
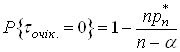 (31)
(31)
Тепер обчислимо ![]() . По-перше, позначимо ймовірність
. По-перше, позначимо ймовірність ![]() того, що за час
того, що за час ![]() обслуговуватиметься більше ніж
обслуговуватиметься більше ніж ![]() заявок, при умові, що зайняті усі
заявок, при умові, що зайняті усі ![]() каналів. Крім того, оскільки потік обслуговування заявок є пуассонівським з параметром
каналів. Крім того, оскільки потік обслуговування заявок є пуассонівським з параметром ![]() , то ймовірність обслуговування
, то ймовірність обслуговування ![]() заявок одним каналом обчислюється за формулою
заявок одним каналом обчислюється за формулою 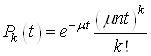 .
.
Якщо на обслуговуванні два канали, тоді кожний канал обслуговує одну заявку незалежно від другого. Отже ймовірність того, що ![]() заявок будуть обслужені двома каналами обчислюється за формулою суми двох незалежних подій
заявок будуть обслужені двома каналами обчислюється за формулою суми двох незалежних подій
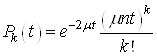 .
.
Далі, продовжуючи аналогічні міркування, можна записати таку формулу для ймовірності обслуговування за час ![]()
![]() заявок, якщо
заявок, якщо ![]() каналів зайняті:
каналів зайняті:
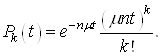 (32)
(32)
Таким чином, якщо врахувати (32)
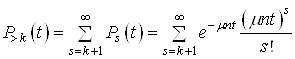 (33)
(33)
Обчислимо ймовірність ![]() за умови (33):
за умови (33):
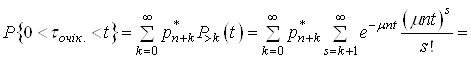
(34)
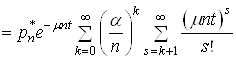 .
.
В останній рівності поміняємо порядок сумування змінних ![]() і
і ![]() . Тоді (34) можна записати у вигляді:
. Тоді (34) можна записати у вигляді:

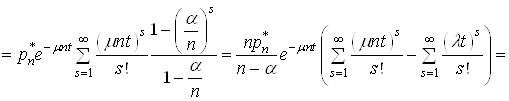
 .
.
Тепер можна записати значення ![]() :
:
 (35)
(35)
Враховуючи (31) і (35) до рівності (28) маємо вираз для функції розподілу часу очікування початку обслуговування у вигляді
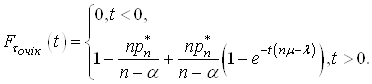 (36)
(36)
Вираз (36) можна спростити і тоді:
 (37)
(37)
Випадкова величина ![]() не є дискретною, бо в точці
не є дискретною, бо в точці ![]() і 1 функція розподілу
і 1 функція розподілу ![]() має розрив. Якщо ввести функцію
має розрив. Якщо ввести функцію  що має похідну
що має похідну 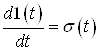 , тоді можна записати щільність розподілу часу очікування обслуговування
, тоді можна записати щільність розподілу часу очікування обслуговування ![]() , тобто
, тобто
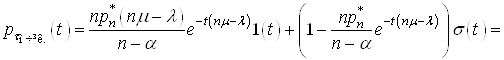
(38)
 ,
,
де 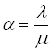 .
.
4. Середній час очікування початку обслуговування
Якщо врахувати (38) і формулу обчислення математичного сподівання випадкової величини, тоді можна обчислити середній час очікування початку обслуговування:
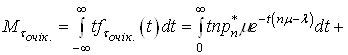
(39)
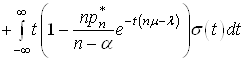 .
.
Відомо, що 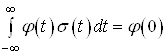 , тому другий інтеграл у (39) дорівнює нулю, тоді
, тому другий інтеграл у (39) дорівнює нулю, тоді
 .(40)
.(40)
Оскільки для існування фінальних ймовірностей достатньо, щоб ![]() , тоді
, тоді 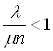 , звідки
, звідки ![]() . Враховуючи це в (40), отримаємо:
. Враховуючи це в (40), отримаємо:
 .(41)
.(41)
5. Середній час перебування заявки у СМО
Позначимо середній час перебування заявки в СМО через ![]() . Середній час перебування заявки в системі складається із часу очікування обслуговування і часу, що йде на обслуговування, тобто
. Середній час перебування заявки в системі складається із часу очікування обслуговування і часу, що йде на обслуговування, тобто
![]() ,
,
тоді
![]() .
.
Враховуючи (41) і те , що 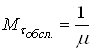 , маємо
, маємо
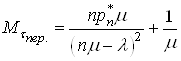 . (42)
. (42)
6. Функція розподілу випадкового часу перебування заявки у СМО
![]()
(43)
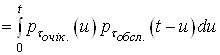 ,
,
де ![]() – щільність розподілу випадкового часу очікування обслуговування, що обчислюється за формулою (38), а
– щільність розподілу випадкового часу очікування обслуговування, що обчислюється за формулою (38), а ![]() – щільність розподілу випадкового часу обслуговування.
– щільність розподілу випадкового часу обслуговування.
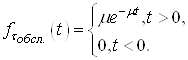
Похожие работы
... , визначення основних характеристик одноканальних систем масового обслуговування вимагає великої обчислювальної роботи, в зв’язку з чим всі розрахунки робляться на комп’ютері. 1.2 Побудова моделей задач масового обслуговування (на прикладі роботи обчислювального центру (ОЦ)) 1.2.1 Модель для імітації виробничої діяльності ОЦ 1.2.1.1 Завдання Розробити модель для імітації виробничої ді ...
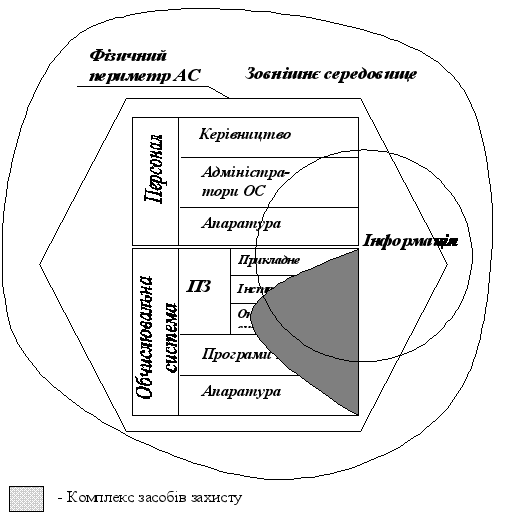
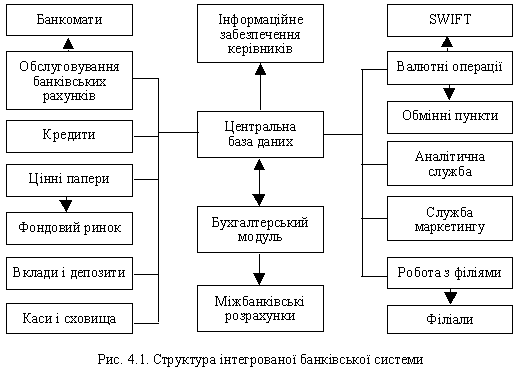
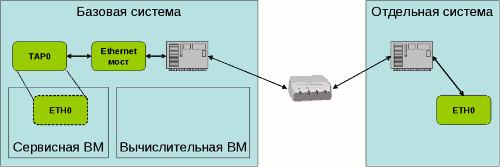
... В АБС АКБ «ПРОМІНВЕСТБАНК» ТА ОЦІНКА РІВНЯ ВРАЗЛИВОСТІ БАНКІВСЬКОЇ ІНФОРМАЦІЇ 3.1 Постановка алгоритму задачі формування та опис елементів матриці контролю комплексної системи захисту інформації (КСЗІ) інформаційних об’єктів комерційного банку В дипломному дослідженні матриця контролю стану побудови та експлуатації комплексної системи захисту інформації в комерційному банку представлена у вигляді ...
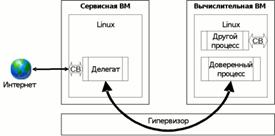
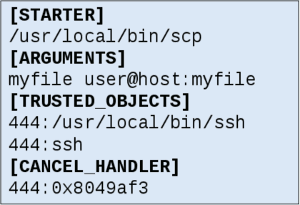
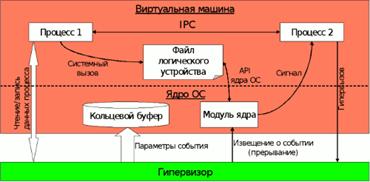
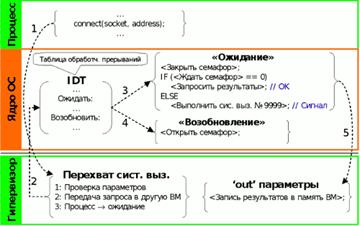
... кування. Якщо запит містить параметри змінної довжини, то доступ до сховища здійснюється тим користувальницьким процесом, який безпосередньо обслуговує запит. 2. Прозоре обслуговування системних викликів Механізм системних викликів в процесорах сімейства x86 може бути реалізований різними способами. Історично для цього використовувалися програмні переривання (інструкція INTn), зокрема, в ...
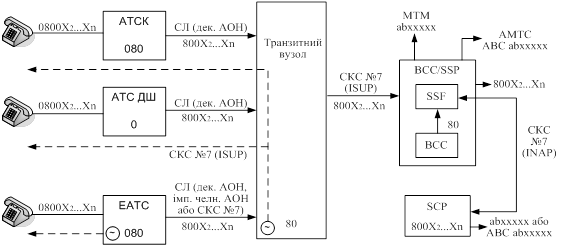
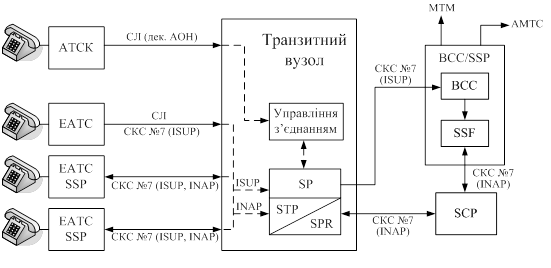
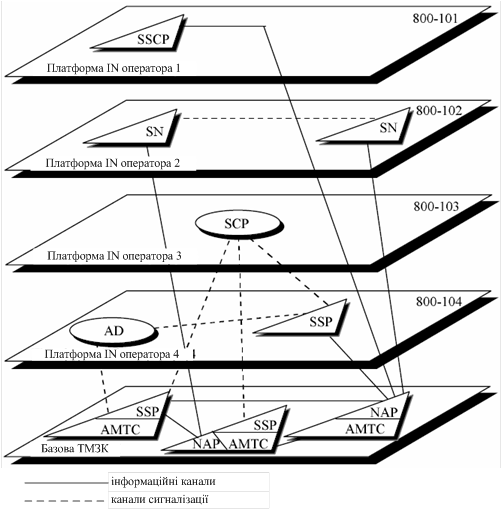
... (SDP, SMP, SMAP і SCEP) не розглядається, оскільки вони не пов'язані з вузлами базової ТМЗК, а способи їхньої реалізації та взаємодії безпосередньо не впливають на останню. 2 Розрахунок часових затримок повідомлень в інтелектуальній надбудові Затримки під час надання послуг IN порівняно з традиційним телефонним з’єднанням зростають через необхідність обміну службовою інформацією між вузлами ...


0 комментариев