Навигация
Расчет статистических показателей
УСЛОВИЕ:
Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности:
| Номер завода | Среднегодовая стоимость основных производственных фондов, млрд. руб. | Объем продукции в сопоставимых ценах, млрд. руб. |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | 3,4 3,1 3,5 4,1 5,8 5,2 3,8 4,1 5,6 4,5 4,2 6,1 6,5 2,0 6,4 4,0 8,0 5,1 4,9 4,3 5,8 7,2 6,6 3,0 6,7 | 3,5 3,3 3,5 4,5 7,5 6,9 4,3 5,9 4,8 5,8 4,6 8,4 7,3 2,1 7,8 4,2 10,6 5,8 5,3 4,9 6,0 10,4 6,9 3,5 7,2 |
С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав четыре группы заводов с равными интервалами. По каждой группе и совокупности заводов подсчитайте:
1. число заводов;
2. среднегодовую стоимость основных производственных фондов - всего и в среднем на один завод;
3. объем продукции - всего и в среднем на один завод;
Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
РЕШЕНИЕ
Сначала рассчитываем шаг интервала по формуле:
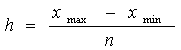 , где
, где
Xmax максимальное значение среднегодовой стоимости ОПФ, Xmax= 8,0;
Xmin - минимальное значение среднегодовой стоимости ОПФ, Xmin = 2,0;
n- Количество групп, n = 4
![]() млн. руб.
млн. руб.
Результаты представим в виде групповой таблицы № 1.
В колонку «Номера заводов» записываем номера заводов, которые попадают в интервалы по группам, затем считаем ОПФ (их среднегодовую себестоимость). Считаем колонку «Всего»: складываем среднегодовую себестоимость по заводам групп, затем « В среднем на 1 завод». Считаем «Валовой продукт» - значения объемов продукции в сопоставимых ценах складываем по заводам групп.
Считаем фондоотдачу:
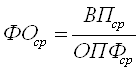
Разбиваем на 4 групп:
I гр.: 2,0 – 3,5 (2,0; 3,0; 3,1; 3,4; 3,5) = 15/5 = 3
Валовой продукт: (2,1; 3,5; 3,3; 3,5; 3,5) = 15,9/4 = 3,98 млрд. руб.;
II гр.: 3,5 – 5,0 (3,8; 4,0; 4,1; 4,1;4,2; 4,3; 4,5; 4,9; 5,1) = 39/9 = 4,3;
Валовой продукт: (4,3; 4,2; 4,5; 5,9; 4,6; 4,9; 5,8; 5,3; 5,8) = 45,3 / 4 = 11,33 млрд. руб.;
III гр.: 5,0 – 6,5(5,2; 5,6; 5,8; 5,8; 6,1; 6,4; 6,5; 6,6; 6,7) = 54,7/9 = 6,08;
Валовой продукт: (6,9; 4,8; 7,5; 6,0; 8,4; 7,8; 7,3; 6,9; 7,2) = 62,8/4 = 15,7 млрд. руб.;
IV гр.: 6,5 – 8,0 (7,2; 8,8) = 15,2 / 2 = 7,6;
Валовой продукт: (10,4; 10,6) = 21 / 4 = 5,25 млрд. руб.;
Используя метод группировок для решения поставленной задачи можно сделать следующие выводы:
1. Параметры фондоотдачи наиболее эффективны в группе предприятий № IV, поскольку максимальное значение этого коэффициента свидетельствует о наиболее эффективном использовании основных фондов в производстве продукции.
2. На этом основании министерству указанной отрасли, куда входят представленные заводы, необходимо рекомендовать проводить группировку предприятий для каждой группы с максимальным числом заводов равным 2.
Таблица № 1
| Величина интервала | № заводов | Число заводов | ОПФ | Валовой продукт | ФОср = ВПср/ОПФср | ||
| Всего | На 1 завод | Всего | На 1 завод | ||||
| 2,0 - 3,5 | 13,23,2,1,3 | 5 | 15 | 3 | 15,9 | 3,98 | 1,06 |
| 3,5 - 5,0 | 7,16,4,8,11,20,10,19,18 | 9 | 39 | 4,33 | 45,3 | 11,33 | 1,16 |
| 5,0 - 6,5 | 6,9,5,21,12,15,13,23,25 | 9 | 54,7 | 6,08 | 62,8 | 15,7 | 1,15 |
| 6,5 - 8,0 | 22,17 | 2 | 15,2 | 7,6 | 21 | 5,25 | 1,38 |
Задача № 2
УСЛОВИЕ:
Имеются следующие данные по областям Центрально-Черноземного района:
| Область | Валовой сбор, Ц. | Урожайность, Ц. / га. |
| 1 | 63000 | 21,0 |
| 2 | 38000 | 19,6 |
| 3 | 29000 | 18,4 |
| 4 | 68000 | 23,2 |
| 5 | 51000 | 19,5 |
Вычислите среднюю урожайность в целом по району. Укажите, какой вид средней нужно применить.
РЕШЕНИЕ
Задача составлена на применение средней арифметической и средней гармонической взвешенных. Выбор вида средней зависит от исходной статистической информации и экономического содержания показателя.
Если в условии задачи даны показатели урожайности по видам сельскохозяйственных культур и валовой сбор, то средняя урожайность будет вычислена по формуле средней гармонической взвешенной:
 , где
, где
Wi = Xi*fi
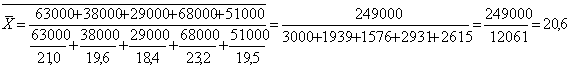
Вывод: Средняя урожайность в среднем по району 20,6 ц / га.
Задача № 3УСЛОВИЕ:
Имеется следующий ряд распределения телеграмм, принятых отделением связи, по числу слов:
| Количество слов в телеграмме | 12 | 13 | 14 | 15 | 16 | 17 | 18 | Итого |
| Число телеграмм | 18 | 22 | 34 | 26 | 20 | 13 | 7 | 140 |
Рассчитайте абсолютные и относительные показатели вариации.
РЕШЕНИЕ
Найдем абсолютные показатели вариации
1. Найдём размах вариации по формуле:
![]() , где
, где
Xmax – максимальное значение признака в совокупности
Xmin - минимальное значение признака в совокупности
18 – 12 = 6 слов.
2. Найдем средне арифметическую взвешенную по формуле
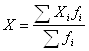
![]()
3. Рассчитаем средне линейное отклонение взвешенное так как данные сгруппированы, по формуле
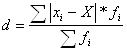
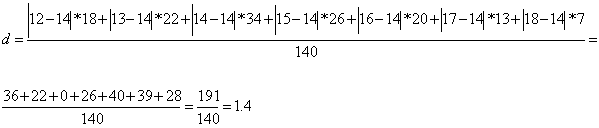 4. Взвешенная дисперсия рассчитывается по формуле
4. Взвешенная дисперсия рассчитывается по формуле

![]()
Похожие работы
... , табличные характеристики связи. Это в свою очередь потребовало решения соответственно теоретико-методологических проблем. Глава 2. Абсолютные и относительные величины 2.1. Понятие, формы выражения и виды статистических показателей Статистическое исследование независимо от его масштабов и целей всегда завершается расчетом и анализом различных по виду и форме выражения статистических ...
... по их запросам статистическая информация предоставляется на платной основе. Статистической информации с ограниченным доступом предоставляется пользователям в соответствии с законодательством Российской Федерации. 2. Формирование единого информационного пространства В процессе осуществления статистического учета Федеральные органы исполнительной власти и их территориальные органы ...
... : х - стаж по специальности; f - накопленная частота. Графики являются важным средством выражения и анализа статистических данных, поскольку наглядное представление облегчает восприятие информации. Графики позволяют мгновенно охватить и осмыслить совокупность показателей - выявить наиболее типичные соотношения и связи этих показателей, определить тенденции развития охарактеризовать структуру и ...
... наблюдения – можно ли распространить результаты выборочной совокупности на генеральную совокупность или нет, следовательно, проверка выборочной совокупности на точность это необходимая часть анализа при несплошном наблюдении. Существуют два вида оценок статистических показателей на точность: точечная и интервальная. Точечная представляет собой оценку параметра в генеральной совокупности одним чи
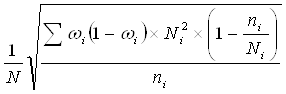
0 комментариев