1 ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
1.1 Размещения – комбинации из n объектов по m (0<=m<=n)
|
Без повторений |
С повторениями |
|
а) отличаются хотя бы одним объектом или б) порядком объектов |
1.2 Перестановки – комбинации из n объектов по n (по n1, n2, … nk)
|
Без повторений |
С повторениями, где
|
|
Отличаются порядком объектов |
1.3 Сочетания – комбинации их n объектов по m
|
|
|
|
Отличаются хотя бы одним объектом |
Пример 1.
На складе имеется 80 лампочек. Из них 30 по 150W, 20 по 100 W, 30 по 60 W. Чему равна вероятность того, что из взятых 10 лампочек 3 лампочки будут по 150 W, 2 лампочки по 100 W.
Решение.
По условию имеем
80=30 + 20 + 30
10=3 + 2 + 5
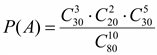 .
.
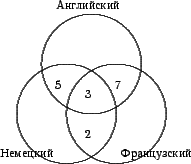
С методической точки зрения основные теоремы теории вероятностей следует представить рядом с диаграммами Вьенна.
2 ВЕРОЯТНОСТИ ЛОГИЧЕСКИ СВЯЗАННЫХ СОБЫТИЙ
(Основные теоремы теории вероятностей)
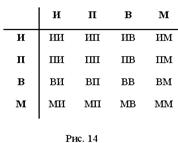
2.1 Совместное появление событий
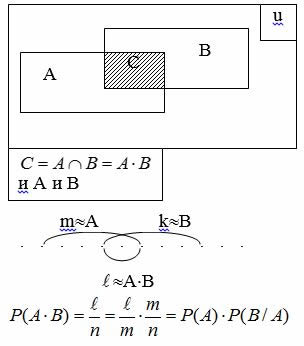 |
1. 2. 3. 4.
|
|
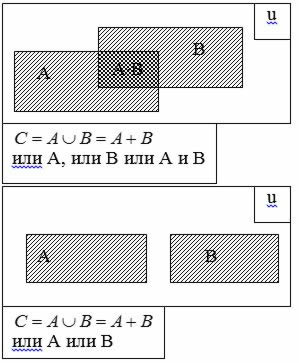
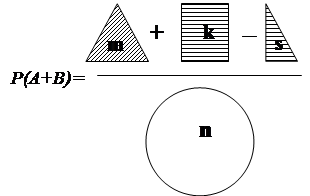
2.2 Появление хотя бы одного из событий |
|
1.
2. 3.
4. 5. |
2.3 Формула полной вероятности
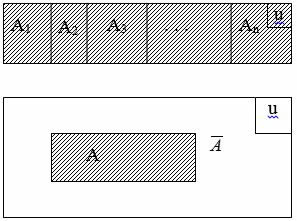
Событие А может произойти с одним из событий , образующих полную группу попарно несовместных событий:
2.4 Формула Байеса
P(Hi/A) – апостериорные вероятности (вероятности после опыта)
По формуле Байеса определяют вероятности того, что причиной осуществления события А стало то или иное событие Hi.
Формула Байеса позволяет «переоценить» вероятности каждой из гипотез Hiпосле поступления новой «информации» относительно осуществления тех или иных наблюдаемых событий.
3 ЛОГИЧЕСКАЯ СХЕМА РЕШЕНИЯ ЗАДАЧ,
СВЯЗАННЫХ СО СЛУЧАЙНЫМИ СОБЫТИЯМИ
При вычислении вероятностей сложных событий необходимо:
-
по условию задачи описать события;
-
записать события в алгебре событий, обращая внимание на союзы: «и» и «или»;
-
выяснить зависимость (независимость), совместность (несовместность) событий;
-
перейти к вероятности в алгебре событий, применив основные теоремы теории вероятностей.
Задача.
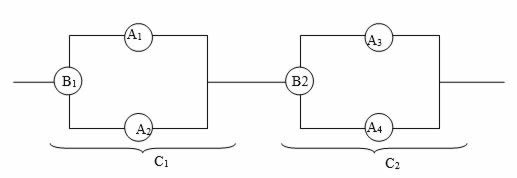
Прибор состоит из четырех узлов А1, А2, А3, А4, выходящих из строя независимо друг от друга, причем узел А2 дублирует узел А1, узел А4 дублирует узел А3. При выходе из строя любого из основных узлов (А1 или А3) происходит автоматическое переключение на дублирующий узел. Надежность (вероятность безотказной работы) в течение заданного времени каждого из узлов соответственно равна Р1, Р2, Р3, Р4. Надежность каждого из переключающих устройств равна Р. Определить надежность прибора.
Решение.
Составим схему работы прибора.
1. По условию задачи опишем события:
А – безотказная работа прибора;
Аi – безотказная работа узлов Аi, 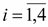 ;
;
Вi – безотказная работа переключающих устройств, i=1, 2;
Сi - безотказная работа обобщенных узлов, i=1, 2.
2. События Аi , Bi и Ci – независимы.
3. Запишем события в алгебре событий:
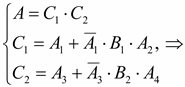
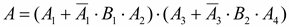
4. Перейдем к вероятности в алгебре событий, имея в виду независимость событий:
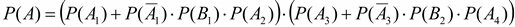 .
.
По условию имеем:
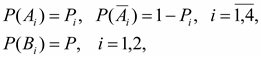
тогда
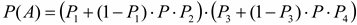 - вероятность безотказной работы прибора.
- вероятность безотказной работы прибора.
Похожие материалы
... обучения, школа предоставляет учащимся право выбора предметов по интересам и склонностям. В соответствии с требованиями была разработана программа факультативного курса по теме «Элементы комбинаторики» для 8 класса. 2.2 Программа факультативного курса Пояснительная записка В математике и ее приложениях часто приходится иметь дело с различного рода множествами и подмножествами: ...
... выборок. 5. Исследовательские проекты и их защита. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Всего 10 5 10 Итого 60 34 Глава 2 Методика обучения школьников основам комбинаторики, теории вероятностей и математической статистики в рамках профильной школы 2.1. Организация при формировании пространственного образа, c использованием ...
... уметь приобретать, обрабатывать и эффективно применять информацию. В ходе выполнения контрольной работы были изучены логические основы работы ЭВМ, основные понятия и операции алгебры логики, а также прикладного программного обеспечения. В настоящее время термин «информация» является одним из самых распространенных. Для переработки информационных ресурсов применяют специальные технологии - ...
... игрок делает выбор из 28 костей. Второй из 28-7=21 костей, третий 14, а четвертый игрок забирает оставшиеся кости. Следовательно, возможно . Размещения и сочетания с повторениями Часто в задачах по комбинаторике встречаются множества, в которых какие-либо компоненты повторяются. Например: в задачах на числа – цифры. Для таких задач при размещениях используется формула , а для сочетаний . Примеры ...
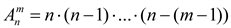 .
.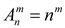 .
.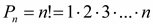 .
.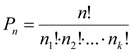 .
.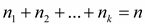 .
.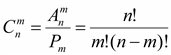 .
.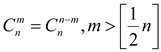 .
.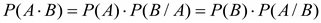
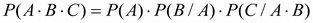
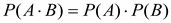 ,
,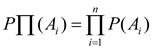 ,
,
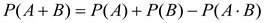 ,
,
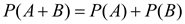 , А×В=V,
, А×В=V,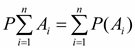 , Ai×Aj=V, i¹j,
, Ai×Aj=V, i¹j,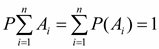 , Ai×Aj=V, i¹j,
, Ai×Aj=V, i¹j,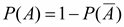 ,
, 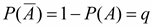 .
.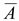 распадается на меньшее число вариантов, чем событие А.
распадается на меньшее число вариантов, чем событие А.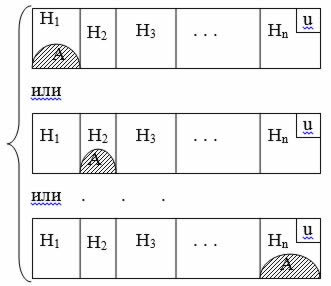
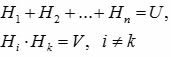
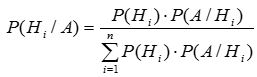

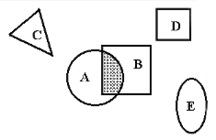



0 комментариев