Ознакомление с логическими элементами, реализующими основные логические функции и формирование навыков анализа и синтеза простых логических схем.
Любое логическое выражение, составленное из nпеременных с помощью конечного числа операций алгебры логики можно рассматривать, как функцию nпеременных. Переменные чаще всего обозначаются символом “Х”, а функция или -![]() или
или![]() , где
, где ![]() - совокупность переменных Х. Переменных может быть сколько угодно много.
- совокупность переменных Х. Переменных может быть сколько угодно много.
Логическая функция и ее переменные могут принимать только два значения, которые часто обозначают “0” и “1”. В электрических схемах состоянию “0” соответствует низкий уровень напряжения, а состоянию “1” - высокий уровень.
Логическая функция может быть задана словесно, аналитическим выражением и таблицей истинности. Самым понятным способом задания является таблица истинности, в которой рассмотрены все возможные комбинации переменных и соответствующие им значения функции.
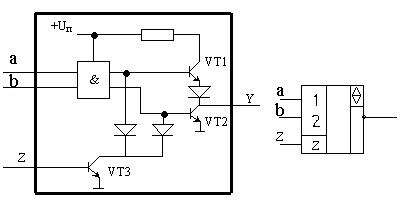
Устройства, реализующие функции алгебры логики называются логическими элементами (ЛЭ). Многие из них выпускаются в интегральном исполнении. Рассмотрим часто встречающиеся ЛЭ для двух переменных. Выпускаются ЛЭ и для большего числа переменных, но и с помощью двухвходовых ЛЭ можно реализовать функцию любого числа переменных, используя операции композиции.
Таблица истинности, условное графическое обозначение и аналитическая форма записи для ЛЭ представлены на рисунках 1.1 ... 1.6.
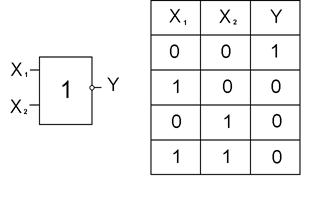
Логический элемент НЕ (рисунок 4.1) реализуют функцию логического отрицания. Функция принимает значение обратное значению переменной. Поэтому этот ЛЭ еще называют инвертором.
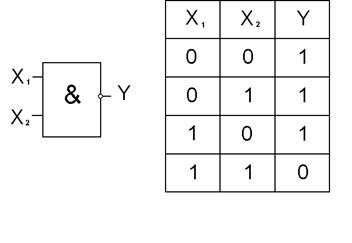
Логический элемент И (рисунок 4.2) реализует функцию логического умножения (конъюнкцию). Функция принимает значение “1”, когда все переменные равны “1”.
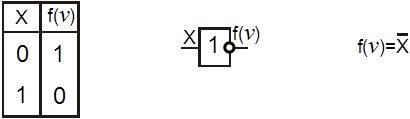
Рисунок 4.1. Элемент НЕ
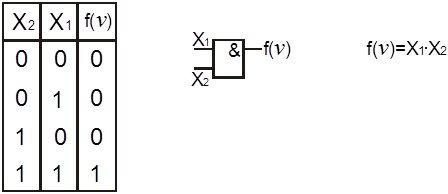
Рисунок 4.2. Элемент И
Логический элемент ИЛИ реализует функцию логического сложения (дизъюнкцию). Функция принимает значение “1”, если хотя бы одна из переменных равна “1”.
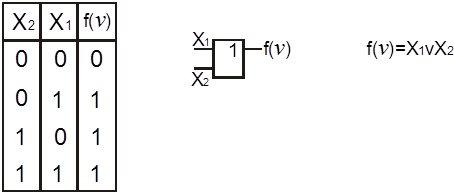
Рисунок 4.3. Элемент ИЛИ

Рисунок 4.4. Элемент И-НЕ
Логический элемент И-НЕ реализует функцию логического умножения с отрицанием. Функция принимает значение “0” (не “1”), когда все переменные равны “1”.
Логический элемент ИЛИ-НЕ реализует функцию логического сложения с отрицанием. Функция принимает значение “0” (не “1”), если хотя бы одна переменная равна “1”.
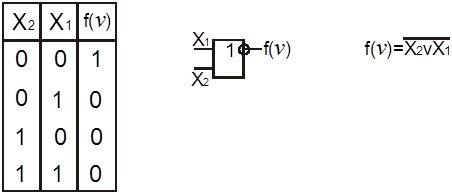
Рисунок 4.5. Элемент ИЛИ-НЕ
Логический элемент “сумма по модулю 2’’ (рисунок 4.6 а) осуществляет операцию, определяющуюся по правилам арифметического сложения двоичных чисел. Функция принимает значение “1”, если число переменных, имеющих значение “1”, нечетное.
Логический элемент “исключающее ИЛИ” (рисунок 4.6 б) реализует функцию, которая принимает значение “1”, когда только лишь одна переменная равна единице.
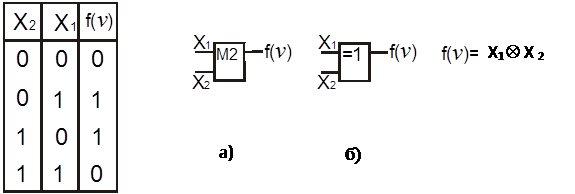
Рисунок 4.6
Аналитическая форма записи для них одинаковая, но функции совпадают только для двух переменных!
Перед тем, как реализовать логическую функцию с помощью ЛЭ, нужно попытаться ее упростить. Это делается с помощью законов и тождеств алгебры логики. Вот некоторые из них
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
К логическим функциям применимы также сочетательный и распределительный законы
![]()
![]()
![]()
![]()
![]()
Набор ЛЭ, с помощью которого можно реализовать сколь угодно сложную функцию, называется функционально полным или базисом. Например, ЛЭ И, ИЛИ, НЕ составляют базис. Имеются базисы, которые содержат только один ЛЭ. Это ЛЭ И-НЕ или ИЛИ-НЕ. Базис из элементов И-НЕ более популярен. Схема, составленная с использованием ЛЭ И, ИЛИ, НЕ удобнее для чтения, но схема, реализованная в базисе, состоящим из одного элемента, имеет часто меньше корпусов микросхем ЛЭ.
При переходе к базису И-НЕ или ИЛИ-НЕ используют правило де Моргана
![]()
![]()
Для практического использования более удобны формулы:
![]()
![]()
Правило де Моргана можно распространить на любое число переменных с помощью законов композиции.
Трехвходовой элемент 3И-НЕ можно использовать, как двухвходовой, оставив один вход не подключенным.
Для преобразования функции более двух переменных и для реализации ее с помощью ЛЭ 2И-НЕ следует применять законы композиции и правило де Моргана, рассмотренные в кратких теоретических сведениях.
Таблицу истинности лучше заполнять таким образом, чтобы номер строки соответствовал двоичному числу, которое составляет комбинация значений переменных, помещенных в эту строку. Младший разряд соответствует переменной Х1 и далее по возрастанию индекса. Двоичное число, как и десятичное, читается слева направо. Нумерация строк начинается с 0 и эта строка помещается вверху таблицы.
![]() Для перебора различных сочетаний переменных удобно использовать счетчик К155ИЕ5 (номер 13). Чтобы счетчик работал, необходимо на один из его входов R (&) подать “0”(лучше использовать гнезда
Для перебора различных сочетаний переменных удобно использовать счетчик К155ИЕ5 (номер 13). Чтобы счетчик работал, необходимо на один из его входов R (&) подать “0”(лучше использовать гнезда![]() ), а вход С соединить с гнездом.
), а вход С соединить с гнездом.
Для сброса счетчика в “0” (на всех выходах при этом устанавливается “0”) необходимо на обоих входах R(&) установить “1”. При каждом отпускании кнопки S (после ее нажатия), двоичное число, записанное в счетчике, увеличивается на 1. Переменные ![]() берутся с выходов счетчика, обозначенных Х, а инверсные значения
берутся с выходов счетчика, обозначенных Х, а инверсные значения ![]() с выходов обозначенных
с выходов обозначенных![]() . Переменная
. Переменная ![]() берется с выхода обозначенного “1”, переменная
берется с выхода обозначенного “1”, переменная ![]() - с выхода, обозначенного “2” и т.д. в порядке возрастания индекса. В этом случае сочетания переменных будут следовать подряд, как они размещены в таблице истинности.
- с выхода, обозначенного “2” и т.д. в порядке возрастания индекса. В этом случае сочетания переменных будут следовать подряд, как они размещены в таблице истинности.
Похожие материалы
... V ~“ должна находиться в нажатом, а кнопка “ВСВ ВНК” в поле надписи “КВУ” - в отжатом состоянии. 4. Методические рекомендации к выполнению работы 4.1. Исследование особенностей функционирования логических элементов ДД1 ¸ ДД4 и определение их функционального назначения. 4.1.1. Задавая различные комбинации входных логических сигналов, определить значение выходного сигнала и по результатам ...
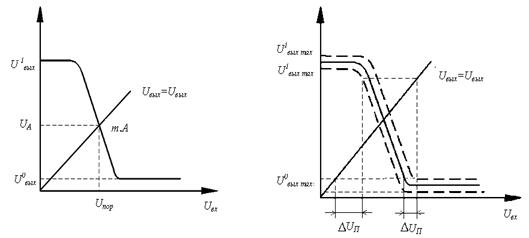
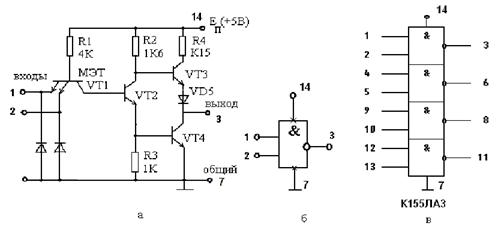
осхемы К155ЛА3 (4 логических элемента 2И-НЕ). Принцип работы ЛЭ И-НЕ ТТЛ Основная особенность микросхем ТТЛ состоит в том, что во входной цепи используется специфический интегральный прибор – многоэмиттерный транзистор (МЭТ), имеющий несколько эмиттеров, объединенных общей базой. Эмиттеры расположены так, что непосредственное взаимодействие между ними через участок базы отсутствует. Поэтому МЭТ ...
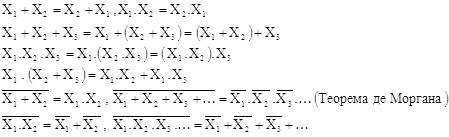
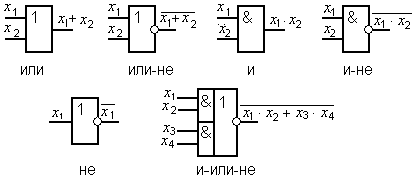
0 комментариев