Введение
В данной курсовой работе исследуется линейная электрическая схема, содержащая динамические элементы. Производится расчёт токов в ветвях электрической цепи до и после коммутации методом контурных токов и методом узловых напряжений, рассчитывается баланс мощностей в цепи до коммутации. Перед произведением всех расчётов по току линеаризуется вольт – амперная характеристика нелинейного элемента (резистора). В процессе расчётов цепи методами контурных токов и узловых потенциалов выясняется какой из методов является наиболее удобным и почему. Исследуется переходный процесс в динамическом элементе классическим и операторным методами. Осваивается метод расчета параметров четырёхполюсника, рассчитывается передаточная функция по заданной координате. Анализируются применяемые методы расчёта переходного процесса в динамических элементах, их достоинства и недостатки. Приобретается опыт применения ПЭВМ.
1 Расчет линейной электрической цепи в схеме до коммутации
1.1 Вольт - амперная характеристика нелинейного элемента
Исходные данные:
|
Еm1 = 208 В; Еm2 = 115 В; j1 = -60°; j2 = 30°; R1 = 90 Ом; R2 = 75 Ом; R4= 90 Ом; |
R3 = 60 Ом; L1 = 24 мГн; L2= 28 мГн; С1 = 5,33 мкФ; С2 = 5 мкФ; f = 350 Гц. |
Искомая функция – UL
Таблица 1 - ВАХ нелинейного элемента
|
u, B |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
80 |
100 |
120 |
140 |
|
i, A |
0 |
0,05 |
0,07 |
0,10 |
0,15 |
0,20 |
0,27 |
0,40 |
0,60 |
0,80 |
1,10 |
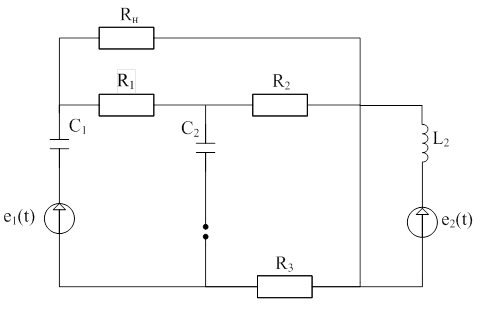
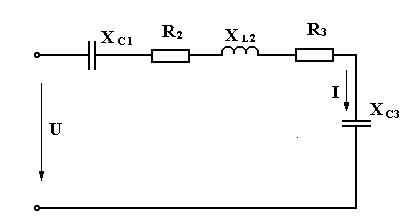
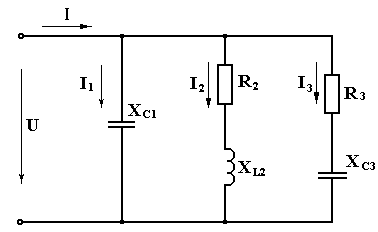
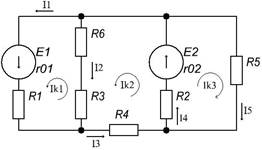
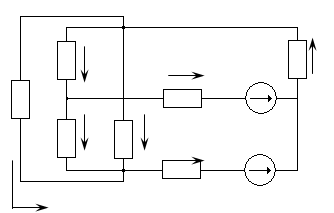
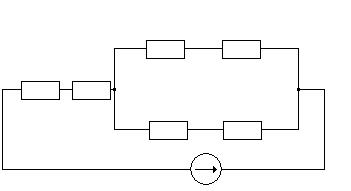
Рисунок 1 – схема электрическая
Для удобства расчета электрической цепи производится линеаризация ВАХ нелинейного элемента. По исходным данным таблицы 1 строится ВАХ. Далее через точку (0;0) пересекая нелинейную характеристику проводится прямая так, чтобы расстояние Dх в точке, соответствующей напряжению 140 В, и Dх в точке, соответствующей напряжению 70 В, были равны между собой. Точка пересечения прямой и нелинейной характеристики будет точкой, для которой определяется статическое сопротивление нелинейного элемента.
RCT = (m U / m I ) · tg α, , ( 1. 1 )
где m U - масштаб напряжения (в одном сантиметре D Вольт);
m I - масштаб тока (в одном сантиметре С Ампер);
α - угол между прямой и осью тока.
График ВАХ нелинейного элемента представлен в приложении А. По графику определяется
m U = 10 В/см; m I = 0,1 А/см; α = 55 °.
По формуле (1.1) определяют
RCT = (10/ 0,1) · tg 55 ° = 142 Ом.
В дальнейших расчетах сопротивление нелинейного элемента принимается равным RНЭ = 142 Ом.
1.2 Подготовка данных для ввода в ПЭВМ
1.2.1 Расчет электрической цепи методом контурных токов
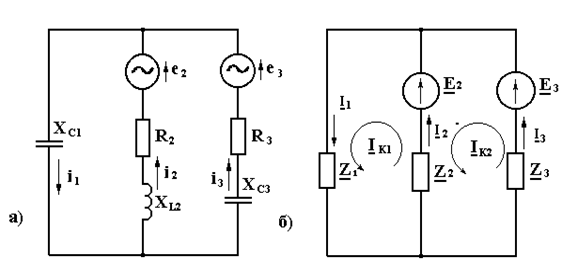
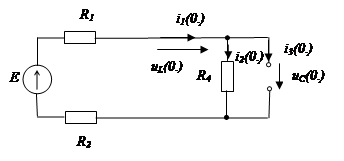
Рассматриваетсясхема до коммутации в соответствии с рисунком , при этом элемент каждой цепи заменяется на эквивалентное комплексное сопротивление в соответствии с рисунком 2
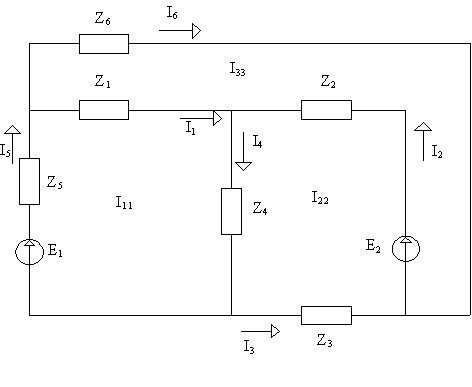
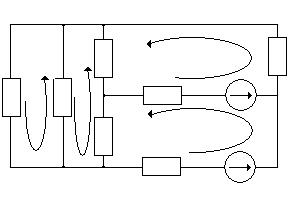
Рисунок 2 – схема замещения
Задаетсянаправление тока в цепи. Расчитывается количество независимых контуров по формуле
k = m – (n – 1),
где m – количество ветвей, m = 6;
n – количество узлов, n = 4.
К=6-(4-1)=3
Следовательно в схеме замещения задают направления трех контурных токов. Рассчитывают значение комплексных сопротивлений и ЭДС.
ω = 2 . π . f = 2 . 3,14 . 350 = 2198 (с-1) ;
Z1 = R1 = 90 Ом;
Z2 = R2 + jXL2 = R2 + ωL2= 75+j2198 * 28 * 10-3= 75 + j61,544 Ом;
Z3 = R3= 60 Ом;
Z4 = - j ХC2 = - j ![]() = -j
= -j ![]() = -j 90,99 Ом;
= -j 90,99 Ом;
Z5 = - j ХC1 = - j![]() = -j
= -j ![]() = -j 85,36 Ом;
= -j 85,36 Ом;
Z6 = Rн =Rст = 143 Ом;
Е1 = Еm1. (cos φ1 + j sin φ1) = 208 . (cos (-60°) +j sin (-60°)) =
= 104 - j 180,13 (В);
Е2 = Еm2. (cos φ2 + j sin φ2) = 115. (cos 30° + sin 30°) = 99,59 + j57,5 (В).
Схема, в соответствии с рисунком 2, используется для построений матрицы при расчете токов и напряжений методом контурных токов, который заключаются в том, что на оснований второго закона Кирхгофа вместо токов в ветвях сначала определяется контурные токи, замыкающиеся в контурах.
Если ток n-ой ветви присутствует в контуре и совпадает по направлению с контурным током, то на пересечении ветви и контура ставится 1. Если ток в ветви не совпадает по направлению с контурным током ставится -1. Если контурный ток не проходит через какую-либо ветвь, ставится 0. Таким образом получают матрицу С.
. . . . . .
I1 I2 I3 I4 I5 I6
![]()
![]() I11 1 0 0 1 1 0
I11 1 0 0 1 1 0
I22 0 1 1 1 0 0
I33 -1 1 0 0 0 1
![]()
![]() 1 0 0 1 1 0
1 0 0 1 1 0
С = 0 1 1 1 0 0
-1 1 0 0 0 1
Полученные значения Z, E матрицы С вводятся в ПЭВМ. Чтобы проверить точность расчёта токи и напряжения в ветвях определяют ещё одним методом – методом узловых потенциалов, который заключается в том, что на основании первого закона Кирхгофа определяется потенциалы в узлах электрической цепи относительно некоторого базисного узла, потенциал которого равен нулю. Падение напряжения на какой – либо ветви равно разности узловых потенциалов на концах этой ветви, а произведение этого напряжения на проводимости ветви равного проходящему через неё току.
1.2.2 Расчет электрической цепи методом узловых потенциалов
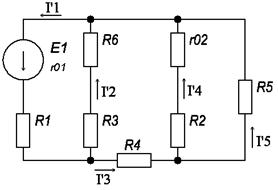
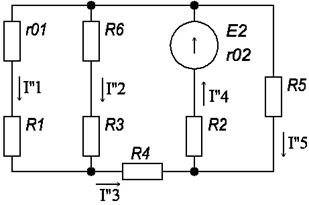
Схеме в соответствии с рисунком 2, заменяется на эквивалентность. Вместо комплексных сопротивлений используется комплексные проводимости, а источники напряжения заменяется источниками тока.
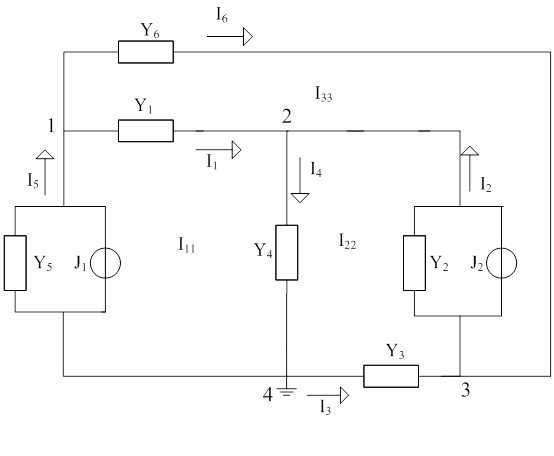
Рисунок 3 – Схема эквивалентная
Определяется величины по формуле
Y=1/Z;
Y1= ![]() =
= ![]() = 0,011111
= 0,011111
Y2= ![]() =
=![]()
Y3= ![]() =
= ![]()
Y4= ![]()
Y5= ![]()
Y6= ![]()
Находятся токи, вырабатываемые источниками
I=E/Z.
I1= ![]() (A)
(A)

В схеме, в соответствии с рисунком 3, обозначают узлы и выбираются базисные узлы (4 узел), потенциал которого равен нулю U4 = 0. Составляются матрицы, в которой строки соответствуют узлам, столбцы – токам в ветвях.
. . . . . .
I1 I2 I3 I4 I5 I6
![]()
![]() 1 узел -1 0 0 0 1 -1
1 узел -1 0 0 0 1 -1
2 узел 1 1 0 -1 0 0
3 узел 0 -1 1 0 0 1
. . . . . .
![]()
![]() I1 I2 I3 I4 I5 I6
I1 I2 I3 I4 I5 I6
-1 0 0 0 1 -1
D = 1 1 0 -1 0 0
0 -1 1 0 0 1
Если ток входит в узел, то записывается в матрице 1, если ток выходит из узла – -1, если ток отсутствует по отношению к рассматриваемому узлу, записывается 0. В результате получают матрицу D.
1.3 Баланс мощности электрической цепи
Баланс мощностей рассчитывается в схеме до коммутации, в соответствии с рисунком 1. Задача состоит в необходимости доказать, что мощность, вырабатываемая источниками равна мощности, потребляемой нагрузкой.
![]() .
.
![]() ,
,
где E1, E2 – комплексные значения э.д.с.,
. .
I1, I2 – сопряжённые значения к комплексным значениям токов I1, I2.
Потребляемая мощность представляет собой сумму активной и реактивной мощностей:
Sпотр = Pакт + jQреакт , для которой
Pакт. = R1Im42+R2 Im62+ R3 Im22+ Rcт Im12
jQреакт = I2 m5XC1 + I2 m4XC2 + I2 m2XL,
.
где Im = Imax определяется по формуле Im =![]() , ток I1 = a + jb берется из приложения Б.
, ток I1 = a + jb берется из приложения Б.
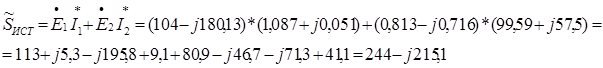
Paкт = 90 (0,097 + 0,027) + 75 (0,662 + 0,512) +
+60 (0,0015 + 0,874) + 142 (0,599+0,047) = 11,1 + 88 + 52,5 + 91,7 = 243,3
jQреак = 61,5 (0,662 + 0,512) – 90,99 (1,267+ 0,779) – 85,36 (1,181 + 0,002) =
= 72,2 – 186,1 – 100,9 = - 214,8
Sпотр =243,3 - j214,8
Из расчетов видно, что мощность вырабатываемая источником равна мощности потребляемой нагрузки
2 Расчет токов и напряжений в цепи после коммутации
2.1 Расчет электрической цепи методом контурных токов
В схеме, в соответствии с рисунком 1, производится коммутация, т. е. размыкается ключ, при этом схема имеет следующий вид.
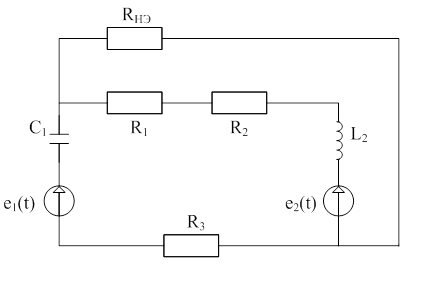
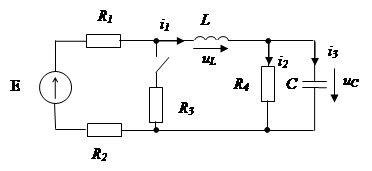
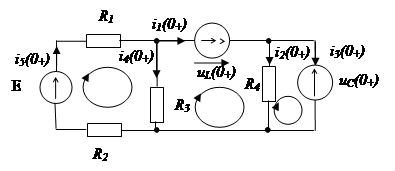
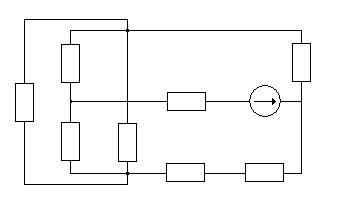
Рисунок 4 – Схема электрическая
Для данной схемы составляется замещение, в соответствии с рисунком 5.
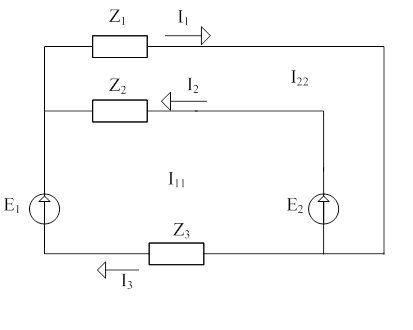
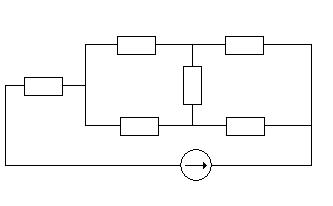
Рисунок 5 – Схема замещения
Для схемы замещения определяется значения сопротивлении z1’, z2’, z3’
Z1’ = RНЭ;
Z2’ = R1 + R2 + j ωL2;
Z3’= - j![]() ;
;
Z1’ = 143 Ом;
Z2’ = 90 + 75 + j61,54 = 165+j61,54 Ом ;
Z3’ = 60- j85,36
В схеме, в соответствии с рисунком 5, задаются направления обхода контурных токов.
В соответствии с рисунком 4, m=3, n=2 где - m число ветвей, n – число узлов.
К=3-(2-1)=2
Аналогично схеме в соответствии с рисунком 2, для соответствии с рисунком 5, составляется матрица С.
С= 0 1 -1
1 1 0
Значения Z и Еэкв, матрицы С вводятся в ПЭВМ для расчета токов в цепи после коммутации.
2.2 Расчет электрической цепи методом узловых потенциалов
Схеме в соответствии с рисунком 5 заменяют на эквивалентную, представленную на рисунке 6.
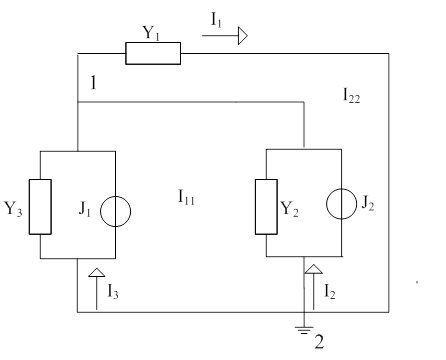
Рисунок 6 – схема эквивалентная
Для данной схемы в соответствий с рисунком 6, определяется значение проводимостей у1’, y2’, y3’
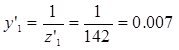
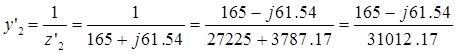
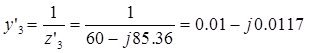
Составляется матрица D, используя сведения описанное в пункте 1.2.1 для методов узловых потенциалов.
![]()
![]() D = -1 1 1
D = -1 1 1
Значения Yэкв, Iэкв, матрица D вводятся в ПЭВМ. При расчете токов в цепи после коммутации двумя методами значения токов должны совпадать. Результаты представлены в приложении Б. Полученные результаты используется в дальнейших расчетах.
3 Расчет переходного процесса в электрической цепи
3.1 Расчет электрической цепи классическим методом
На рисунке 7 представлена исходная схема после коммутации.
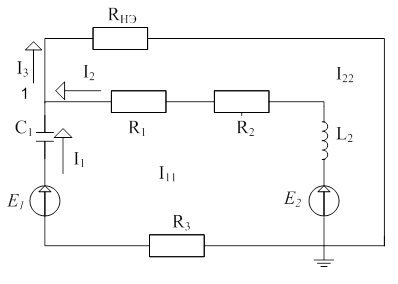
Рисунок 7 – схема электрическая после коммутации
Переходный процесс в разветвлённой цепи описывается системой линейных дифференциальных уравнений с постоянными коэффициентами, общее решение которых находится как сумма принуждённой и свободной составляющих.
В приложении Б представлены токи в ветвях. В соответствий с рисунком 7 через индуктивность проходит ток I2, значение которого определяется в приложении Б.
I2= 0,036 + j0,621
Значение тока I2 записывается в синусоидальной форме
iL(t) = Im Sin(wt + j),
iL(t) = iLпр(t)
Im = ![]() ,
,
j = arctg ![]()
Im = ![]() ,
,
j = arctg ![]()
iL(t) =0.619 Sin(wt + 1.51),
UпрL(t)=38.09 cos(wt+1.51)
Свободная составляющая представляют собой общее решение системы однородных линейных дифференциальных уравнений. Для получения характеристического уравнения составляется система уравнений по законам Кирхгофа, в соответствии с рисунком 7.
![]()
![]() ,
,
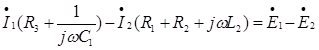 ,
,
![]() .
.
Производится замена jwL = qL, ![]() =
=![]()
![]() и записывается система однородных уравнений:
и записывается система однородных уравнений:
![]()
![]() ,
,
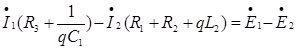 ,
,
![]() .
.
Данная система уравнений имеет решение, отличное от нуля, если определить системы равен нулю т.е:
![]()
![]()
![]()
![]() 1 1 -1 142 1 1 -1
1 1 -1 142 1 1 -1
D = 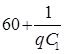
![]() 0 =
0 = 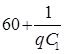
![]() 0 =
0 =
0 ![]() 142 142
142 142 ![]() 0
0
= - (18420+1,68q + ![]() + 5253 + 23430 + 3,97q) = -5,65 – 47103 -
+ 5253 + 23430 + 3,97q) = -5,65 – 47103 - ![]()
Определитель приравнивается к нулю, таким образом получается характеристическое уравнение второго порядка
5,65q2 + 47103q + 57,59 * 106 = 0
Находятся корни характеристического уравнения
D = 2218692609 – 1301534000 = 917158609
q1=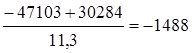
q2=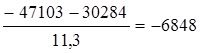
Для действительных отрицательных корней решение однородного дифференциального уравнения имеет следующий вид:
iLсв(t) = A1eq1t + A2eq2t .
где, А1 и А2 постоянные интегрирования, которые определяется из начальных условий.
q1 и q2 - корни характеристического уравнения
Для нахождения постоянного интегрирования рассматривается система уравнении.
![]() iL(-0) = iLпр + A1 + A2,
iL(-0) = iLпр + A1 + A2,
iL¢(-0) = iLпр¢ + q1A1 + q2A2.
Ток на индуктивности iL(0) на основании первого закона коммутаций равен току на индуктивности. В соответствии с рисунком 2 определяется ток I2 до коммутации и приложение Б.
I2= 0,813 + j 0,716
Выражение I2 записывается в синусоидальной форме
Im = ![]() ,
,
j = arctg ![]()
iL(-0) =1,0803 sin(wt + 0,715),
при t=0
iLпр(t)=1,083* sin(2380t+ 0,715)
iL(-0) =1 ,083* sin(0.715)=0.71
iL¢(-0)=2380 * 0,754 = 1796
iLпр(0)=0,619*0,998=0,62
iLпр¢(0)= 1360,5 * 0,052=71
UL(-0)=66.65*cos(wt + 0,715),
При известных значениях iL(-0), iL¢(-0), iLпр(0), iLпр¢(0), q1, q2 система уравнений примет вид:
![]() 0,71=0,62+A1+A2
0,71=0,62+A1+A2
![]() 1796 = 71 – 1488 A1 – 6848 A2
1796 = 71 – 1488 A1 – 6848 A2
A1=0,09 – A2
1796= 71 – 134 + 1488A2 – 6848 A2
1859 = - 5360 A2
![]() A2 = -0,35
A2 = -0,35
A1 = 0,44
![]()
Зная величинуiLсв , находится ULсв
UL(t)=L![]()
![]()
График переходного процесса, рассчитанного классическим методом , представлен в приложении В.
3.2 Расчёт электрической цепи операторным методом.
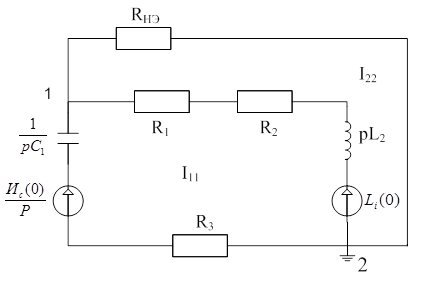
Рисунок 8 – эквивалентная операторная схема в режиме после коммутации
В данной схеме задаются направления двух контурных токов.
К=m-(n-1)=3-(2-1)=2
Данная формула справедлива для действительных и комплексных корней.
Составим уравнения по методу контурных токов и запишем полученную сиcтему уравнений в матричном виде:
![]()
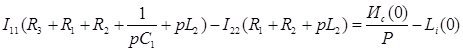
![]()
Составится матрица сопротивлений и находится определитель
D = 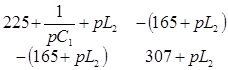 =
=
=69075 + 225 pL2 + 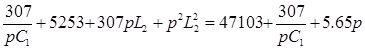
Определитель приравнивается к нулю и определяется корни характеристического уравнения. При это полученные корни p1 и p2 должны быть равным, получившимся в классическом методе.
5.65 p2 + 47103p + 57.59 *106=0
p1= -1488
p2=-6848
![]()
![]() Затем определяется определитель D1
Затем определяется определитель D1
D1 = 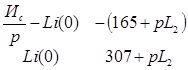
Значение Ис(-0) и iL(-0) в данных выражениях берутся из приложении Б при t=0 . В схеме до коммутации
Ис(-0) = I1*Xc1= (0.312 + j0.166) * (-j85.36)= 14.16 – j 26.6
Иm = ![]()
j = arctg ![]()
Uc(-0) =30.15 sin(wt – 1.082)=-26.6,
iL(-0) =0.71
![]()
![]() D1 =
D1 = 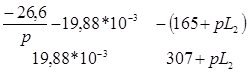 = =
= =![]()
![]()
![]() D2 =
D2 = 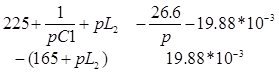 = =
= =![]()
Затем вычисляются контурные токи:
![]() ;
; ![]()
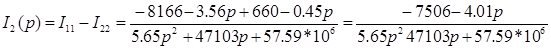
Так как изображения имеет сложный вид, используется теорема разложения
![]() ,
,
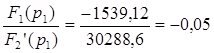
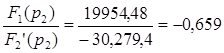
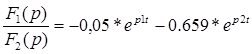
![]()
График переходного процесса , рассчитанного операторным методом представлен в приложении Г.
4 Определение параметров четырехполюсника
Рассматривается четырехполюсник относительно зажимов ЭДС в схеме в соответствии с рисунком 4
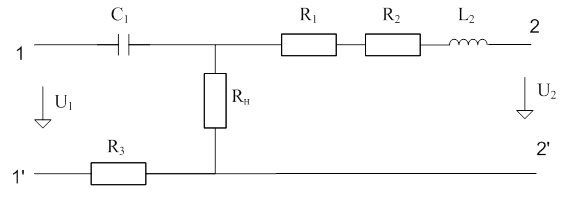
Рисунок 9 – схема четырехполюсника
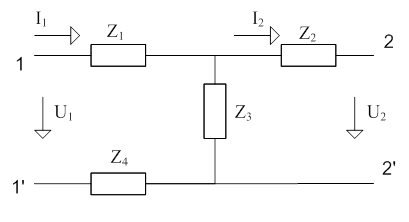
Рисунок 10 – схема замещения
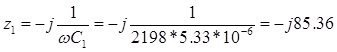
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() .
.
Где - 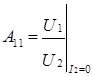 обратный коэффициент передачи по напряжению, рассчитывается в режиме холостого хода на выходе.
обратный коэффициент передачи по напряжению, рассчитывается в режиме холостого хода на выходе.
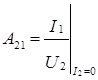 проводимость передачи от входа к выходу, рассчитывается в режиме холостого входа при разомкнутом выходе.
проводимость передачи от входа к выходу, рассчитывается в режиме холостого входа при разомкнутом выходе.
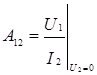 сопротивление передачи от входа к выходу при коротком замыкании выхода.
сопротивление передачи от входа к выходу при коротком замыкании выхода.
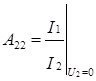 обратный коэффициент передачи по току, рассчитывается в режиме короткого замыкания на выходе.
обратный коэффициент передачи по току, рассчитывается в режиме короткого замыкания на выходе.
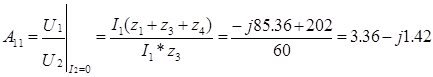
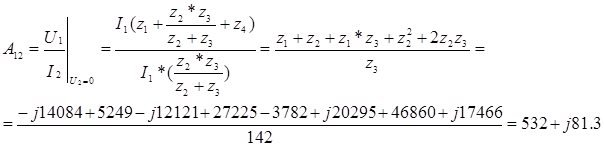
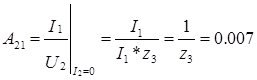
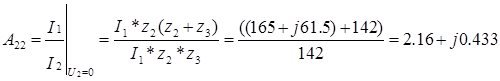
4.1 Передаточная функция
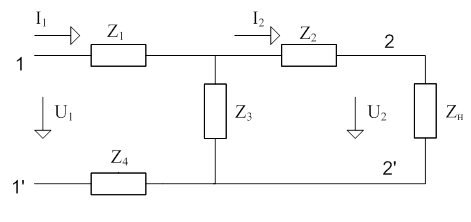
Рисунок 12 – схема замещения
Передаточная функция тока:
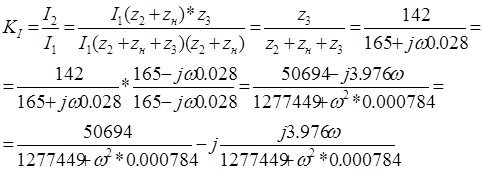
Модуль этих комплексных отношений представляет собой, амплитудно - частотную характеристику, а их аргументы – фаза – частотную характеристику четырехполюсника.
АЧХ: ![]()
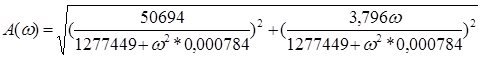
ФЧХ: ![]()
Заключение
В данной курсовой работе был подробно изучен переходный процесс, методы расчета переходного процесса, определение параметра четырехполюсника, правила построении АЧХ и ФЧХ.
В разделе 1.2 курсовой работы были изучены и применены на практике методы расчета токов и напряжении (метод контурных токов и метод узловых потенциалов). Расчеты проводились с использованием ПВЭМ.
В разделе 1.3 курсовой работы рассчитывается баланс мощности, потребляемой нагрузкой и вырабатываемая активными элементами цепи. Приблизительно равно этих двух значений доказывает справедливость закона баланса мощностей и верность расчетов.
В разделе 3 осуществляется переходного процесса классическим и операторным методом. В обоих случаях расчета переходного процесса были одинаковые и комплексно сопряженные корни р1 и р2 характеристического уравнения. Это доказывает правильность расчетов обоих методов.
В разделе 4 и 4.1 были рассчитаны параметры четырехполюсника и найдена передаточная функция по току, используя которую получили графическое изображение АЧХ (см. Приложении Д) и ФЧХ (см. Приложении Е).
Похожие материалы
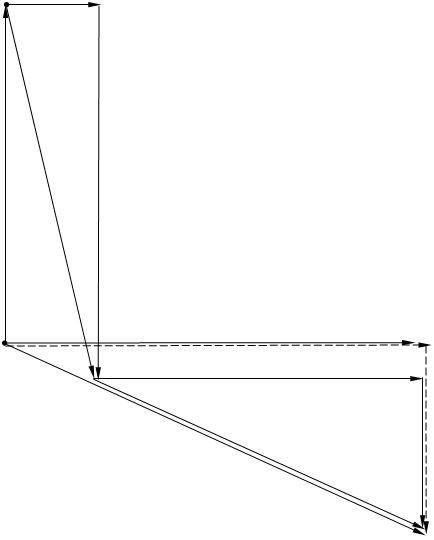
... диаграмма построена на рисунке 4. Ia2 MI= 0,5 А/см МU= 25 В/см I2 I1=Ip1 Ip2 OIa U Ia3 I3 Ip3 Ip I Рисунок 43 Расчёт сложных цепей переменного тока символическим методом Электрическая схема цепи и комплексная схема замещения представлены на рисунке 5а и б соответственно. Рисунок 5 Намечаем в независимых контурах заданной цепи, как показано на рисунке 5б, ...
... по частям, как в пункте I}= II. В результате получаем закон изменения искомой величины при подаче на вход цепи импульса заданной формы: Расчет и построение графика спектральной плотности прямоугольного импульса Основой спектрального анализа является то, что любой непрерывный сигнал можно представить как периодический с периодом . Энергия ...
... контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат - потенциалы точек с учетом их знака. рис.1.7 1.2 Расчет нелинейных электрических цепей постоянного тока Построить входную вольтамперную характеристику схемы (рис.1.8) Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные ...
... будущего специалиста к работе на производстве. 1. Анализ электрического состояния линейных электрических цепей постоянного тока Схема электрической цепи постоянного тока: R2 I2 R7 I5 E1,r02 I7 R1 I3 R5 R3 R4 I4 I6 I1 E2,r02 R6 Рис.1.0 ...
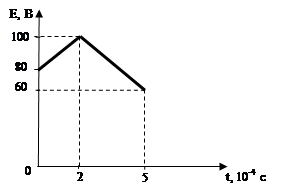
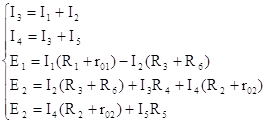

0 комментариев