Содержание:
1. Содержание – 1стр.
2. Введение -2стр.
3. Вариационный ряд – 3стр.
4. Статический ряд – 4стр.
5. Гистограмма. Полигон. – 6стр.
6. Критерий согласия x-квадрата - 7стр.
7. Вычисление дисперсии и СКО – 8стр.
8. Интервальная оценка – 9стр.
9. Вывод – 10стр.
10. Список используемой литературы – 11стр
1
Введение
Метод Пирсона.
При измерениях с многократными наблюдениями обработка результата проводится по-разному в зависимости от числа серий наблюдений, условий и числа измерений в каждой серии, значимости систематических погрешностей и ряда других факторов. В простейшем случае, когда выполнена одна серия наблюдений с числом измерений n<12, ограничиваются вычислением среднего арифметического результата наблюдений (математического ожидания) и оценки его среднеквадратического отклонения (СКО).
В общем случае порядок обработки результатов прямых измерений с многократными наблюдениями регламентирует ГОСТ 8.207-76. При этом необходимо выполнить следующие операции:
1. Исключить систематические погрешности.
2. Исключить грубые погрешности (промахи) из результатов наблюдений.
3. вычислить среднее арифметическое исправленных результатов наблюдений, которое принимается за результат измерений.
4. Вычислить оценку СКО результата наблюдения.
5. Вычислить оценку СКО результата измерения.
6. Проверить гипотезу о том, что результаты наблюдений принадлежат нормальному закону распределения.
7. Вычислить доверительные границы случайной погрешности (случайной составляющей погрешности) результата измерения.
8. Вычислить границу неисключенной систематической погрешности (не исключенных остатков систематической погрешности) результата измерения
9. Вычислить доверительные границы погрешности результата измерения. На практике наиболее важным и распространенным является случай, когда нет необходимости оценки неисключенных остатков систематических погрешностей.
Рассмотрим для данного случая порядок обработки результатов измерений на конкретном примере (например, на измерении напряжения на выходе электронного узла).
Покажем пример обработки результатов прямых измерений с многократными наблюдениями. Для простоты, наглядности и обозримости вычислений возьмем ограниченное количество величин n = 20, хотя для применения метода Пирсона необходимо, чтобы количество наблюдений было значительно больше (50 и более).
2
|
1. Получен ряд наблюдений случайной величины, который представлен таблице Ряд наблюдений
|
Таб.1
|
Преобразуем ряд наблюдений в вариационный ряд, т.е. установим результаты наблюдений в порядке возрастания. |
Вариационный ряд
|
№ п/п |
xi |
№ п/п |
xi |
|
1 |
98 |
11 |
102 |
|
2 |
98 |
12 |
102 |
|
з |
100 |
13 |
102 |
|
4 |
100 |
14 |
102 |
|
5 |
100 |
15 |
104 |
|
6 |
100 |
16 |
104 |
|
7 |
102 |
17 |
104 |
|
8 |
102 |
18 |
104 |
|
9 |
102 |
19 |
106 |
|
10 |
102 |
20 |
106 |
Таб.2
3
2. Вычислим статистические оценки распределения случайной величины: математическое ожидание my, дисперсию Dx, СКО 5x величины X:
![]() ;
;
![]() =98+98+100+100+100+100+102+102+102+102+102+102+102+102+104+104+104+104+106+106=
=98+98+100+100+100+100+102+102+102+102+102+102+102+102+104+104+104+104+106+106= ![]() = 102
= 102
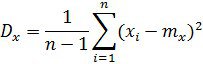
![]() =
= ![]() (16+16+4+4+4+4+4+4+4+4+16+16)=5,0326
(16+16+4+4+4+4+4+4+4+4+16+16)=5,0326
![]()
Произведем проверку критерия согласия с (нормальным) законом распределения по методу Пирсона.
3. Построим статистический ряд, т.е. таблицу, в которой приведены длины разрядов Jiв порядке их соответствия оси абсцисс измеряемой величины X, количество niзначений величины xiоказавшихся в том или ином разряде, а также статистические частоты Р*iи вероятности Рiпопадания измеряемой величиныХ интервал (xi: xi+1):
![]() =
=![]()
Вычисляем число разрядов kпо формуле Стерджесса:
k=3,322 lgn + 1 = 3,322 lg20 +1 = 3,322 x 1,3010 + 1 ≈ 5 = 5
Находим, что число разрядов k= 5.
Разделение интервалов (xi: xi+1) производится по желанию оператора, но рекомендуется выбирать равномерно для облегчения вычислений.
4
Статистический ряд
|
Обозначение |
Разряды |
||||
|
|
97-99 |
99-101 |
101-103 |
103-105 |
105-107 |
|
|
2 |
4 |
8 |
4 |
2 |
|
|
0,1 |
0,2 |
0,4 |
0,2 |
0,1 |
|
|
0,0779 |
0,2372 |
0,3436 |
0,2372 |
0,0779 |
Таб.3
![]() =
= ![]() =
= ![]() = 0,1
= 0,1
![]() =
= ![]() =
= ![]() = 0,2
= 0,2
![]() =
= ![]() =
= ![]() = 0,4
= 0,4
![]() =
= ![]() =
= ![]() = 0,2
= 0,2
![]() =
= ![]() =
= ![]() = 0,1
= 0,1
4. Построим гистограмму (рис.1) и полигон (рис.2) как графическое представление статистической плотности распределения.
Вид гистограммы и полигона позволяет выбрать в качестве теоретической модели нормальный закон распределения, который принимаем за рабочую гипотезу для идентификации.
5
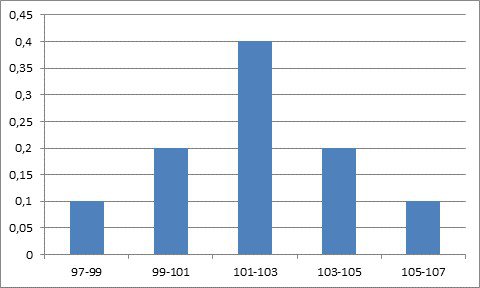
Рис.1Гистограмма
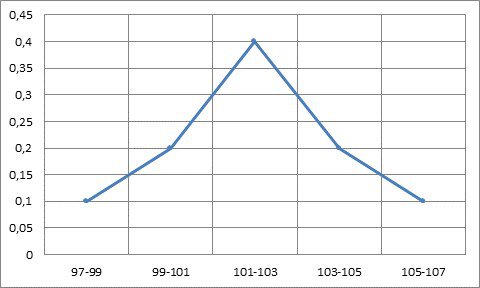
Рис.2Полигон
5. Определяем значение границ интегрирования и вычисляем значения функции Лапласа Ф для этих значений по сути существующим таблицам .
Вычисления теоретических вероятностей ![]() производим по формуле:
производим по формуле:
![]() =
= ![]() -
-![]() ;
;
6
![]() =
= ![]() =
= ![]()
= 0,0910 ![]() 0,0131 = 0,0779
0,0131 = 0,0779
![]() =
= ![]() =
= ![]()
= 0,3282 ![]() 0,0910 = 0,2372
0,0910 = 0,2372
![]() =
= ![]() =
= ![]()
= 0,6718 ![]() 0,3282 = 0,3436
0,3282 = 0,3436
![]() =
= ![]() =
= ![]()
= 0,9090 ![]() 0,6718 = 0,2372
0,6718 = 0,2372
![]() =
= ![]() =
= ![]()
= 0,9869 ![]() 0,9090 = 0,0779
0,9090 = 0,0779
Результаты заносим в таб.3 (четвертая строка).
6. Вычисляем критерий согласия x-квадрат (Пирсона):
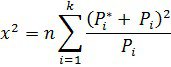
7
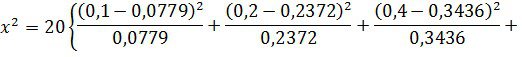
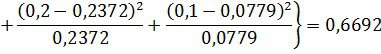
7. Находим число степеней свободы распределения x-квадрат с учетом того, что достаточное число независимых условий sдля нормального закона равно трем:
r=k![]() s=5
s=5![]() 3= 2.
3= 2.
8. Из таблицы распределения x-квадрата (для значения ![]() 0,6699 и r=2)
0,6699 и r=2)
Находим вероятность согласия эмпирического и теоретического законов распределения P= 0,65, интерполируя между соседними величинами.
На основании полученной вероятности P= 0,65 можно сделать вывод , что гипотеза о соответствии эмпирического закона нормальному не противоречит экспериментальным данным.
9. Вычислим дисперсию и СКО результата измерений
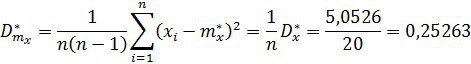
![]()
8
10. Определим значения квантилей закона распределения ![]() при доверительной вероятности
при доверительной вероятности ![]() 0,95. Для нашего случая n
0,95. Для нашего случая n![]() 1=20
1=20![]() 1=19.
1=19.
![]() 2,09
2,09
11. Произведем интервальную оценку результата наблюдения ![]() .
.
Вычислим доверительные границы и запишем результат в виде:
![]()
Это означает, что 95% всех наблюдаемых значений распределяются в пределах от 95,3 до 104,7.
12. Произведем интервальную оценку результата измерений ![]() , предварительно вычислив доверительные границы. Результат измерения представим в виде
, предварительно вычислив доверительные границы. Результат измерения представим в виде
![]() , т.е.
, т.е.
![]()
9
Вывод
С достоверностью 95% можно утверждать, что математическое ожидание среднего арифметического результата наблюдений находится в пределах от 101 до 103 В.
10
Список используемой литературы:
1. «Метрология» Каратаев Р.Н., Гогин В.А. 2007г.
2. «Краткий справочник метролога» Брянский Л.Н., ДойниковА.С. 1991г.
3. Информационные материалы с сайта tso.ru, sonel.ru, metrologu.ru/info
11
Похожие материалы
... видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы 1. Цель математической обработки результатов эксперимента; 2. Виды измерений; 3. Типы ошибок измерения; 4. Свойства случайных ошибок; 5. Почему среднеарифметическое значение случайной величины при нормальном законе ее ...
... Как видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы Цель математической обработки результатов эксперимента; Виды измерений; Типы ошибок измерения; Свойства случайных ошибок; Почему среднеарифметическое значение случайной величины при нормальном законе ее распределения является ...
... результату измерений из совокупности результатов измерений, выполняемых по одной и той же аттестованной МВИ– приписанные погрешности измерений. 3. Отражающие близость отдельного, экспериментально полученного результата измерений к истинному значению измеряемой величины – статистические оценки характеристик погрешности измерений (статистические оценки погрешности измерений). Нормы погрешности ...
... – оценку дисперсии : (2.3.10) Таким образом мы доказали, что для нормально распределенных данных СКО является лучшей оценкой дисперсии. Обработка результатов совместных измерений При совместных измерениях полученные значения используются для построения зависимостей между измеряемыми величинами. Рассмотрим многофакторный эксперимент, по результатом которого должна быть построена ...
... иные нарушения, включая разглашение государственной или коммерческой тайны, государственные инспекторы могут быть привлечены к ответственности в соответствии с законодательством Российской Федерации. 3.9. Основы квалиметрии [47] Квалиметрия — раздел метрологии, изучающий вопросы измерения качества. Здесь используются те же законы и правила, что и в области измерения физических величин, но есть ...
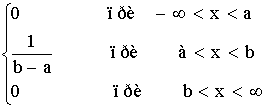
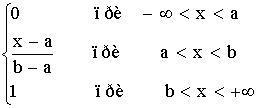
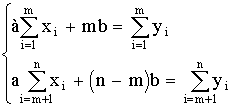
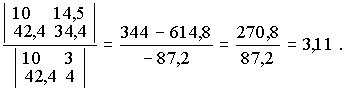


0 комментариев