Қазақстан Республикасының Білім және ғылым министрлігі
әл-Фараби атындағы Қазақ ұлттық университеті
Ахымбек М.Е.
ТӨРТІНШІ РЕТТІ ЖАЙ ДИФФЕРЕНЦИАЛДЫҚ ОПЕРАТОРЛАРДЫҢ СПЕКТРАЛЬДЫҚ ҚАСИЕТТЕРІ
ДИПЛОМДЫҚ ЖҰМЫС
мамандығы 5B060100 – «Математика»
Алматы 2015
Қазақстан Республикасының Білім және ғылым министрлігі
әл – Фараби атындағы Қазақ ұлттық университеті
Іргелі математика кафедрасы
«Қорғауға жіберілді»
Кафедра меңгерушісі
ф.-м.ғ.д., профессор ______________ Б.Е. Кангужин
ДИПЛОМДЫҚ ЖҰМЫС
Тақырыбы: «ТӨРТІНШІ РЕТТІ ЖАЙ ДИФФЕРЕНЦИАЛДЫҚ ОПЕРАТОРЛАРДЫҢ СПЕТРАЛЬДЫҚ ҚАСИЕТТЕРІ»
мамандығы 5B060100 – «Математика»
Орындаған М.Е. Ахымбек
Ғылыми жетекші
т.ғ.д.,профессор Ж.А. Токибетов
Норма қадағалаушы А.М. Тлеулесова
Алматы, 2015
РЕФЕРАТ
Бітіру жұмысы 46 бет, 2 бөлім, кіріспе және қорытынды, сонымен бірге 19 пайдаланған әдебиеттер тізімінен тұрады.
Бітіру жұмысында күшейтілген емес регуляр шекаралық шарттарға ие жай дифференциалдық операторлардың спектральдық қасиеттері зерттелген. Жәнеде екінші ретті дифференциалдық оператордың ойылған кесіндіде бірінші регуляризацияланған ізі есептелді.
Күшейтілген емес регуляр шекаралық шарттарға ие жай дифференциалдық оператордың меншікті мәндері мен меншікті функцияларының асимптотикасы табылып, алынған меншікті функцияларының жүйесі базис құру, құрмауы тексерілді. Жәнеде екінші ретті дифференциалдық оператордың ойылған кесіндідегі Гельфанд – Левитан формуласы тектес бірінші регуляризацияланған ізі есептелген.
Түйін сөздер: дифференциалдық оператор, спектральдық теория, меншікті мән, меншікті функция, базис, ойылған кесінді, бірінші регуляризацияланған із.
РЕФЕРАТ
Выпускная работа изложена на 46 листах, содержит 2 главы, введение и заключение, использовано 19 литературных источников.
В работе исследованы спектральные свойства простых дифференциальных операторов, порожденные регулярно, но не усиленно регулярными краевыми условиями. Вычислен первый регуляризованный след оператора дифференцирования второго порядка в проколотом отрезке.
Найдены асимптотики собственных значений и собственных функций оператора дифференцирования, порожденного регулярными, но не усиленно регулярными краевыми условиями. Исследовано базисность систем собственных функций. Для оператора дифференцирования второго порядка получена формула первого регуляризованого следа типа Гельфанда – Левитана.
Ключевые слова: дифференциальный оператор, спектральная теория, собственное значение, собственная функция, базис, проколотый отрезок, первый регуляризованный след.
ABSTRACT
Final work is presented on 46 sheets, contains 2 chapters, maintenance and conclusion , applied 19 references.
We study the spectral properties of fourth – order differential operators with regular but not strongly regular boundary conditions. And calculate the first regularized trace of second - order differential operator in the punctured segment.
We consider some class of non strongly regular boundary value problems for fourth – order differential operators. We obtain asymptotic formulas for eigenvalues and eigenfunctions of these boundary value problems. Then, using these asymptotic formulas, we prove that system of eigenfunctions does not form basis. There are found the formulas of the first regularized trace (of the type of abstract Gel’fand – Levitan formula) of the two – fold differentiation operator in a punctured segment.
Keywords: differential operator, spectral theory, eigenvalue, eigenfunction, basis, punctured segment, the first regularized trace.
МАЗМҰНЫ
| КІРІСПЕ | 5 | |
| 1. | ҚАРАПАЙЫМ СЫЗЫҚТЫҚ ДИФФЕРЕНЦИАЛДЫҚ ОПЕРАТОРЛАР | 6 |
| 1.1 | Негізгі анықтамалар | 6 |
| 1.2 | Дифференциалдық оператордың меншікті мәндері мен меншікті функциялары | 13 |
| 1.3 |
| 18 |
| 2. | ЕКІНШІ РЕТТІ ДИФФЕРЕНЦИАЛДЫҚ ОПЕРАТОРДЫҢ ОЙЫЛҒАН КЕСІНДІДЕГІ БІРІНШІ РЕГУЛЯРИЗАЦИЯЛАНҒАН ІЗІ | 34 |
| 2.1 | Есептің қойылуы және нәтижелер | 34 |
| 2.2 | Характеристикалық анықтауыш | 36 |
| 2.3 | Негізгі нәтиженің дәлелдеуі | 40 |
| ҚОРЫТЫНДЫ | 44 | |
| ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ | 45 | |
КІРІСПЕ
Жұмыстың бірінші тарауында регуляр шекаралық шарттардың әр түріне жеке тоқталып, төртінші ретті дифференциалдық оператор үшін регуляр, оның ішінде күшейтілген және күшейтілген емес шекаралық шарттарды бөліп алып. Сол әр шарттқа сәйкес дифференциалдық оператордың меншікті функцияларының асимптотикасын алып, олардың базис болу болмауын тексереміз.
Шекаралық шарттар күшейтілген регуляр болған жағдайда оператордың меншікті және қосалқы функциялары ![]() кеңістігінде Рисс базисін құратыны белгілі. Бұл айтылғанды ең алғаш В.П. Михайлов көрсетті. Дәл осы нәтиже Кессельман Г.М. жұмыстарында, және Данфорд Н. мен Шварц Т. монографиясында бар. Бұл жұмыстардың барлығында да, дәлелдеу оператор мен оның түйіндес операторының нормаланған меншікті және қосалқы функциялар жүйесінің бесселдік екендігіне әкелінді.
кеңістігінде Рисс базисін құратыны белгілі. Бұл айтылғанды ең алғаш В.П. Михайлов көрсетті. Дәл осы нәтиже Кессельман Г.М. жұмыстарында, және Данфорд Н. мен Шварц Т. монографиясында бар. Бұл жұмыстардың барлығында да, дәлелдеу оператор мен оның түйіндес операторының нормаланған меншікті және қосалқы функциялар жүйесінің бесселдік екендігіне әкелінді.
Кессельман Г.М. жұмыстарында шекаралық шарттары регуляр бірақ күшейтілген емес регуляр болатын дифференциалдық оператордың меншікті және қосалқы функциялары базис құрмайтындай мысалдар көрсеткен. Себебі бұл жағдайларда оператор Данфорд Н. мағынасында спектральды болмайды, демек бұл жағдайда оператордың меншікті және қосалқы функциялары Рисс базисін құрмайтыны белгілі. Бұл жайтты, оператордың меншікті мәндері асимптотикалық жақын орналасқандығымен түсіндіруге болады, демек келесідей асимптотикаға ие
![]()
![]() болғанда. Соның ішінде жақын орналасқан меншікті мәндерге сәйкес меншікті функциялар бір біріне тең емес, бірақта арасындағы бұрыш нөлге ұмтылады. Дәл осындай жағдайларда оператордың меншікті және қосалқы функциялар жүйесі базис құрмайды.
болғанда. Соның ішінде жақын орналасқан меншікті мәндерге сәйкес меншікті функциялар бір біріне тең емес, бірақта арасындағы бұрыш нөлге ұмтылады. Дәл осындай жағдайларда оператордың меншікті және қосалқы функциялар жүйесі базис құрмайды.
Екінші ретті дифференциалдық операторларға қарағанда төртінші ретті шекаралық шарттары күшейтілген емес регуляр болатын дифференциалдық операторлардың спектральдық теориясы азырақ дамыған. Бұған байланысты тек жекеленген жұмыстар ғана бар.[3,4] Бұл дипломдық жұмыста алдағы уақытта дәл осы шекаралық шарттар күшейтілген емес регуляр болатын төртінші ретті дифференциалдық операторлардың спектральдық қасиеттері зерттеледі.
Ал екінші тарауда екінші ретті дифференциалдық оператордың ойылған кесіндідегі Гельфанд – Левитан формуласы тектес бірінші регуляризацияланған ізі есептелген.
1 ҚАРАПАЙЫМ СЫЗЫҚТЫҚ ДИФФЕРЕНЦИАЛДЫҚ ОПЕРАТОРЛАР
1.1 Негізгі анықтамалар
![]() элементтерінің
элементтерінің ![]() жиынтығы сызықтық кеңістік деп аталады, егерде:
жиынтығы сызықтық кеңістік деп аталады, егерде:
1. ![]() -да кез-келген
-да кез-келген ![]() элементтерінің келесідей қасиеттер орындалатындай
элементтерінің келесідей қасиеттер орындалатындай ![]() қосындысы анықталса:
қосындысы анықталса:
i. егер ![]() онда
онда ![]()
ii. ![]()
iii. ![]()
iv. ![]() -да “нөлдік” элемент 0 табылады және
-да “нөлдік” элемент 0 табылады және![]() кез-келген
кез-келген ![]() үшін
үшін ![]()
2. ![]() -да
-да ![]() элементін
элементін ![]() санына келесідей қасиеттер орындалатындай
санына келесідей қасиеттер орындалатындай ![]() көбейтіндісі анықталса:
көбейтіндісі анықталса:
i. егер ![]() онда
онда ![]()
ii. ![]()
iii. ![]()
iv. ![]() (сол жағында – 0 саны, оң жағында – нөлдік элемент);
(сол жағында – 0 саны, оң жағында – нөлдік элемент);
v. ![]()
vi. ![]()
Және де ![]() элементі
элементі ![]() арқылы белгіленеді, өйткені iii, vi, iv қасиеттерінен
арқылы белгіленеді, өйткені iii, vi, iv қасиеттерінен
![]()
![]() -дағы
-дағы ![]() элементтері осы кеңістіктің векторлары деп аталады.
элементтері осы кеңістіктің векторлары деп аталады.
Егерде ![]() кеңістігінде кез-келген нақты санға көбейту амалы анықталса, онда
кеңістігінде кез-келген нақты санға көбейту амалы анықталса, онда ![]() нақты кеңістік деп аталады; ал егерде кез-келген комплекс санға көбейту амалы анықталса, онда
нақты кеңістік деп аталады; ал егерде кез-келген комплекс санға көбейту амалы анықталса, онда ![]() комплекс кеңістік деп аталады.
комплекс кеңістік деп аталады. ![]() түріндегі өрнекті
түріндегі өрнекті ![]() элементтерінің сызықтық комбинациясы деп аталады. Сызықтық комбинация тривиалды деп аталады, егерде
элементтерінің сызықтық комбинациясы деп аталады. Сызықтық комбинация тривиалды деп аталады, егерде ![]() сандарының барлығы нөлге тең болса, ал кері жағдай да тривиалды емес деп аталады.
сандарының барлығы нөлге тең болса, ал кері жағдай да тривиалды емес деп аталады. ![]() векторлары сызықты тәуелді деп аталады, егерде олардың қандай да бір тривиалды емес сызықтық комбинациясы нөлге тең болса, сызықтық тәуелсіз деп аталады, егерде ондай сызықтық комбинация табылмаса.
векторлары сызықты тәуелді деп аталады, егерде олардың қандай да бір тривиалды емес сызықтық комбинациясы нөлге тең болса, сызықтық тәуелсіз деп аталады, егерде ондай сызықтық комбинация табылмаса.
![]() кеңістігін ақырлы өлшемді соның ішінде
кеңістігін ақырлы өлшемді соның ішінде ![]() - өлшемді дейміз, егерде сол кеңістікте
- өлшемді дейміз, егерде сол кеңістікте ![]() және
және ![]() -нан көп емес сызықтық тәуелсіз векторлар табылса, және сәйкесінше сол
-нан көп емес сызықтық тәуелсіз векторлар табылса, және сәйкесінше сол ![]() векторды
векторды ![]() кеңістігінің базисы дейміз. Ал егерде
кеңістігінің базисы дейміз. Ал егерде ![]() -да шексіз көп сызықтық тәуелсіз векторлар табылса, онда
-да шексіз көп сызықтық тәуелсіз векторлар табылса, онда ![]() ақырсыз өлшемді кеңістік деп аталады.
ақырсыз өлшемді кеңістік деп аталады. ![]() -ты
-ты ![]() -дың ішкеңістігі дейміз, егерде
-дың ішкеңістігі дейміз, егерде ![]() -тың элементтерінің кез-келген сызықтық комбинациясы осы
-тың элементтерінің кез-келген сызықтық комбинациясы осы ![]() -тың өзінде жатса.
-тың өзінде жатса.
Айталық, ![]() жоғарыда берілген
жоғарыда берілген ![]() кеңістігінің қандай да бір ішкеңістігі болсын.
кеңістігінің қандай да бір ішкеңістігі болсын. ![]() -ның әрбір
-ның әрбір ![]() элементіне
элементіне ![]() -дың қандай да бір
-дың қандай да бір ![]() элементін сәйкес қоятын
элементін сәйкес қоятын ![]() функциясын
функциясын ![]() кеңістігінде анықталған, анықталу облысы
кеңістігінде анықталған, анықталу облысы ![]() болатын оператор деп атаймыз. Көп жағдайда
болатын оператор деп атаймыз. Көп жағдайда ![]() -тың орнына
-тың орнына ![]() деп те жаза беруге болады.
деп те жаза беруге болады.
![]() облысы
облысы ![]() операторының анықталу облысы екенін көрсету үшін
операторының анықталу облысы екенін көрсету үшін ![]() -ның орнына
-ның орнына ![]() деп те жаза беруге болады. Барлық
деп те жаза беруге болады. Барлық ![]() векторларының жиынын
векторларының жиынын ![]() операторының мәндер облысы деп атап
операторының мәндер облысы деп атап ![]() немесе
немесе ![]() деп белгілейді.
деп белгілейді.
![]() операторын сызықтық деп атаймыз, егерде
операторын сызықтық деп атаймыз, егерде ![]() ішкеңістік және кез-келген
ішкеңістік және кез-келген ![]() векторлары мен кез-келген
векторлары мен кез-келген![]() саны үшін
саны үшін
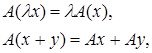
шарттары орындалса.
![]() кеңістігінде
кеңістігінде ![]() және
және ![]() операторлары сәйкес келеді деп атаймыз, сонда және тек сонда, егерде олардың анықталу облыстары
операторлары сәйкес келеді деп атаймыз, сонда және тек сонда, егерде олардың анықталу облыстары ![]() тең болса және
тең болса және
![]()
кез-келген ![]() үшін орындалса.
үшін орындалса.
![]() операторы
операторы ![]() операторының кеңейуі деп аталып және
операторының кеңейуі деп аталып және ![]() немесе
немесе ![]() деп жазылады, егерде
деп жазылады, егерде ![]() және
және ![]() -да екі оператор сәйкес келсе. Және бұл жағдай да
-да екі оператор сәйкес келсе. Және бұл жағдай да ![]() операторы
операторы ![]() операторының тарылуы деп аталады.
операторының тарылуы деп аталады.
Алдағы уақытта біз тек сызықтық операторлар қарастыратын болғандықтан сызықтық оператор терминының орнына жәй ғана оператор деп айта береміз.
Келесідей өрнекті
![]() (1.1.1)
(1.1.1)
сызықтық дифференциалдық өрнек деп атаймыз. ![]() функцияларын осы сызықтық дифференциалдық өрнектің коэффициенттері, ал
функцияларын осы сызықтық дифференциалдық өрнектің коэффициенттері, ал ![]() санын сызықтық дифференциалдық өрнектің реті деп атаймыз. Бұл жұмыста
санын сызықтық дифференциалдық өрнектің реті деп атаймыз. Бұл жұмыста 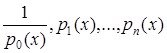 функциялары тағайындалған ақырлы
функциялары тағайындалған ақырлы ![]() интервалында үзіліссіз деп санаймыз, ал кейбір жағдайларда қосымша шарттар қойылады. Яғни, байқағанымыздай кез-келген
интервалында үзіліссіз деп санаймыз, ал кейбір жағдайларда қосымша шарттар қойылады. Яғни, байқағанымыздай кез-келген ![]() функциясы үшін
функциясы үшін ![]() анықталған және ол
анықталған және ол ![]() кесіндісінде үзіліссіз функция болады.
кесіндісінде үзіліссіз функция болады.
![]() функциясын және оның
функциясын және оның ![]() ретке дейінгі туындыларының
ретке дейінгі туындыларының ![]() және
және ![]() нүктелердегі мәндерін сәйкесінше келесідей белгілейік
нүктелердегі мәндерін сәйкесінше келесідей белгілейік
![]() (1.1.2)
(1.1.2)
Енді ![]() арқылы (1.2)-дегі айнымалылырға қатысты құрылған сызықтық форманы белгілейік, яғни
арқылы (1.2)-дегі айнымалылырға қатысты құрылған сызықтық форманы белгілейік, яғни ![]() келесідей түрде болады
келесідей түрде болады
![]() (1.1.3)
(1.1.3)
Егер де осындай түрдегі бірнеше форма берілсе ![]() онда
онда
![]() (1.1.4)
(1.1.4)
теңдіктерін шекаралық шарттар деп атайды.
![]() арқылы (1.1.4) шекаралық шарттарын қанағаттандыратын
арқылы (1.1.4) шекаралық шарттарын қанағаттандыратын ![]() функцияларының жиынтығын белгілейік.
функцияларының жиынтығын белгілейік. ![]() жиыны
жиыны ![]() -ның сызықтық ішкеңістігі екені айқын, және де ол
-ның сызықтық ішкеңістігі екені айқын, және де ол ![]() -ге тең болады сонда және тек сонда, егерде (1.4) шекаралық шарттар мүлде жоқ болса.
-ге тең болады сонда және тек сонда, егерде (1.4) шекаралық шарттар мүлде жоқ болса.
Айталық, қандай да бір ![]() дифференциалдық өрнегі мен (1.1.4) шарттар арқылы анықталған қандай да бір көпбейне берілсін. Әрбір
дифференциалдық өрнегі мен (1.1.4) шарттар арқылы анықталған қандай да бір көпбейне берілсін. Әрбір ![]() функциясына
функциясына ![]() функциясын сәйкес қояйық. Бұл сәйкестік анықталу облысы
функциясын сәйкес қояйық. Бұл сәйкестік анықталу облысы ![]() -ға тең сызықтық оператор болады. Ол операторды
-ға тең сызықтық оператор болады. Ол операторды ![]() арқылы белгілейік, яғни, егерде
арқылы белгілейік, яғни, егерде ![]() және де
және де ![]() болса, онда
болса, онда ![]() операторының анықталуы бойынша
операторының анықталуы бойынша
![]()
екені белгілі. Демек ![]() операторы
операторы ![]() дифференциалдық өрнегі мен (1.1.4)-ші шекаралық шарттарынан туындаған дифференциалдық операторы деп аталады.
дифференциалдық өрнегі мен (1.1.4)-ші шекаралық шарттарынан туындаған дифференциалдық операторы деп аталады.
Яғни, байқағанымыздай бір ғана дифференциалдық өрнек, шекаралық шарттарды әр түрлі таңдау арқылы әр түрлі дифференциалдық операторларды туындатуы мүмкін. Егерде, дербес жағдай да, (1.1.4) шекаралық шарттар жоқ болатын болса, онда берілген операторымыздың анықталу облысы ![]() болады және де біз оны
болады және де біз оны ![]() арқылы белгілейміз. Демек, бұл оператор тура осы дифференциалдық өрнектен туындаған басқа операторлардың барлығының кеңейтілуі болатыны айқын.
арқылы белгілейміз. Демек, бұл оператор тура осы дифференциалдық өрнектен туындаған басқа операторлардың барлығының кеңейтілуі болатыны айқын.
![]() формаларының кейбіреулері қалғандарының сызықтық комбинациясы да болуы мүмкін, яғни ондай жағдайда сызықтық комбинация болатын форма қалғандарының салдары болып қалғандықтан, ол форманы қарастырмай-ақ алып тастаса болады. Сол себепті,
формаларының кейбіреулері қалғандарының сызықтық комбинациясы да болуы мүмкін, яғни ондай жағдайда сызықтық комбинация болатын форма қалғандарының салдары болып қалғандықтан, ол форманы қарастырмай-ақ алып тастаса болады. Сол себепті, ![]() формаларын басын бастап сызықтық тәуелсіз формалар деп қарастырған жөн, яғни бұл формалардың коэффициенттерінен құрылған матрицаның рангысын
формаларын басын бастап сызықтық тәуелсіз формалар деп қарастырған жөн, яғни бұл формалардың коэффициенттерінен құрылған матрицаның рангысын ![]() -ге тең деп алса болады. Егер
-ге тең деп алса болады. Егер ![]() болса, онда (1.1.4) шекаралық шарттар тек келесідей түрде ғана болады, ал бұл шарттардан туындаған операторды қысқаша
болса, онда (1.1.4) шекаралық шарттар тек келесідей түрде ғана болады, ал бұл шарттардан туындаған операторды қысқаша ![]() деп белгілейміз.
деп белгілейміз.
Біртекті шекаралық есеп деп келесідей түрдегі
![]() (1.1.5)
(1.1.5)
![]() (1.1.6)
(1.1.6)
шарттарды қанағаттандыратын ![]() функциясын табу есебін айтамыз. Айталық,
функциясын табу есебін айтамыз. Айталық, ![]() операторы
операторы ![]() дифференциалдық өрнегі мен (1.1.6)-шы шекаралық шарттардан туындаған оператор болсын. Демек, біртекті шекаралық есеп, ол анықталу облысы
дифференциалдық өрнегі мен (1.1.6)-шы шекаралық шарттардан туындаған оператор болсын. Демек, біртекті шекаралық есеп, ол анықталу облысы ![]() -ға тең, сол анықталу облысында
-ға тең, сол анықталу облысында ![]() операторы 0-ге айналатын
операторы 0-ге айналатын ![]() функцияларын табу болып табылады. Кез-келген біртекті шекаралық есептің нөлдік шешімі бар екені белгілі, оны тривиалды шешім деп атаймыз. Демек біздің мақсат тривиалды емес шешімнің бар жоқтығын анықтау, яғни
функцияларын табу болып табылады. Кез-келген біртекті шекаралық есептің нөлдік шешімі бар екені белгілі, оны тривиалды шешім деп атаймыз. Демек біздің мақсат тривиалды емес шешімнің бар жоқтығын анықтау, яғни ![]() болатын шешім.
болатын шешім.
Енді қандай шарттар орындалғанда біртекті шекаралық есептің тривиалды емес шешімі бар болатынын анықтайық. Айталық, ![]() функциялары
функциялары ![]() теңдеуінің сызықтық тәуелсіз шешімдері болсын. Сызықтық дифференциалдық операторлар теориясынан
теңдеуінің сызықтық тәуелсіз шешімдері болсын. Сызықтық дифференциалдық операторлар теориясынан ![]() теңдеуінің кез-келген шешімі мына түрде екені белгілі
теңдеуінің кез-келген шешімі мына түрде екені белгілі
![]()
бұл жердегі ![]() -тұрақтылар. Жоғарыдағы шешімді (1.1.6) шарттарға қойсақ келесідей біртекті сызықтық алгебралық теңдеулер жүйесін аламыз:
-тұрақтылар. Жоғарыдағы шешімді (1.1.6) шарттарға қойсақ келесідей біртекті сызықтық алгебралық теңдеулер жүйесін аламыз:
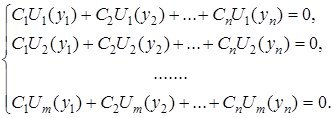 (1.1.7)
(1.1.7)
![]() арқылы келесі матрицаның рангысын белгілейік
арқылы келесі матрицаның рангысын белгілейік
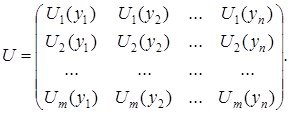 (1.1.8)
(1.1.8)
Демек, (1.1.7)-ші теңдеу ![]() тұрақтыларына қатысты тәуелсіз
тұрақтыларына қатысты тәуелсіз ![]() шешімге ие, яғни, шекаралық есептіңде
шешімге ие, яғни, шекаралық есептіңде ![]() тәуелсіз шешімі болады. Сол себепті:
тәуелсіз шешімі болады. Сол себепті:
1. Егер ![]() матрицасының рангысы
матрицасының рангысы ![]() тең болса, онда біртекті шекаралық есептің дәл
тең болса, онда біртекті шекаралық есептің дәл ![]() тәуелсіз шешімі болады.
тәуелсіз шешімі болады.
2. а) Біртекті шекаралық есептің тривиалды емес шешімі бар болады, сонда және тек сонда, егер ![]() матрицасының рангы
матрицасының рангы ![]() дифференциалдық оператордың реті
дифференциалдық оператордың реті ![]() -нан кіші болса.
-нан кіші болса.
ә) Егер ![]() болса, онда біртекті шекаралық есептің тривиалды емес шешімі бар болады.
болса, онда біртекті шекаралық есептің тривиалды емес шешімі бар болады.
б) Егер ![]() болса, онда біртекті шекаралық есептің тривиалды шешімі бар болады, сонда және тек сонда, егер
болса, онда біртекті шекаралық есептің тривиалды шешімі бар болады, сонда және тек сонда, егер ![]() матрицасының анықтауышы нөлге тең болса.
матрицасының анықтауышы нөлге тең болса.
Айта кететіні, ![]() матрицасының рангысы фундаметалдық шешімдер жүйесін таңдаудан тәуелсіз. Және де сол рангты шекаралық есептің рангысы деп атайды.
матрицасының рангысы фундаметалдық шешімдер жүйесін таңдаудан тәуелсіз. Және де сол рангты шекаралық есептің рангысы деп атайды.
Айталық, келесі дифференциалдық өрнектің
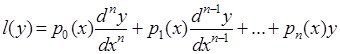
![]() коэффициенттері
коэффициенттері ![]() аралығында
аралығында ![]() ретке дейін үзіліссіз дифференциалдансын (
ретке дейін үзіліссіз дифференциалдансын (![]() ретімен қоса). Және
ретімен қоса). Және ![]() және
және ![]() функциялары
функциялары ![]() кеңістігінен алынған кез-келген функциялар болсын. Келесі өрнекті
кеңістігінен алынған кез-келген функциялар болсын. Келесі өрнекті ![]() рет бөліктеп интегралдау арқылы:
рет бөліктеп интегралдау арқылы:
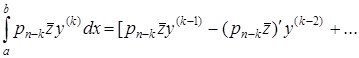
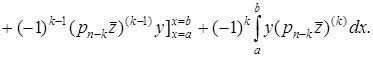 (1.1.9)
(1.1.9)
Осы өрнекте енді ![]() қойып, шыққан теңдіктердің барлығын қоссақ, келесідей формулаға келеміз
қойып, шыққан теңдіктердің барлығын қоссақ, келесідей формулаға келеміз
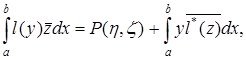 (1.1.10)
(1.1.10)
бұл жердегі,
![]() (1.1.11)
(1.1.11)
және де ![]() келесі айнымалылыларға тәуелді бисызықтық форма
келесі айнымалылыларға тәуелді бисызықтық форма
![]()
![]()
(1.1.11) түрде анықталған дифференциалдық өрнек ![]() дифференциалдық өрнегіне түйіндес деп аталады. Ал (1.1.10) формула Лагранж формуласы деп аталады. Түйіндес өрнекке Лагранж формуласын қайтадан қолдансақ келесідей теңдіктің дұрыс екеніне көз жеткізу оңай
дифференциалдық өрнегіне түйіндес деп аталады. Ал (1.1.10) формула Лагранж формуласы деп аталады. Түйіндес өрнекке Лагранж формуласын қайтадан қолдансақ келесідей теңдіктің дұрыс екеніне көз жеткізу оңай
![]()
Енді түйіндес шекаралық шарттар мен түйіндес оператор ұғымдарын еңгізейік. Айталық, ![]() формалары
формалары ![]() айнымалыларынан тәуелді сызықтық тәуелсіз формалар болсын.
айнымалыларынан тәуелді сызықтық тәуелсіз формалар болсын. ![]() жағдайында қандайда бір
жағдайында қандайда бір ![]() формаларымен толықтырайық және жаңадан сызықтық тәуелсіз
формаларымен толықтырайық және жаңадан сызықтық тәуелсіз ![]() формалары пайда болсын. Бұл формалардың сызықтық тәуелсіздігінен
формалары пайда болсын. Бұл формалардың сызықтық тәуелсіздігінен ![]() айнымалыларын
айнымалыларын ![]() формаларының сызықтық комбинациялары ретінде өрнектеуге болады. Сол табылған теңдіктерді
формаларының сызықтық комбинациялары ретінде өрнектеуге болады. Сол табылған теңдіктерді ![]() бисызықтық формасына қойғанда,
бисызықтық формасына қойғанда, ![]() формамыз
формамыз ![]() формаларына тәуелді сызықтық біртекті форма болады.
формаларына тәуелді сызықтық біртекті форма болады. ![]() айнымалыларының алдындағы коэффициенттері
айнымалыларының алдындағы коэффициенттері ![]() айнымалыларының сызықтық комбинациялары. Оларды
айнымалыларының сызықтық комбинациялары. Оларды
![]()
Сонда Лагранж формуласын келесідей түрде жазса болады
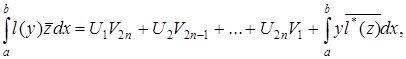 (1.1.12)
(1.1.12)
![]() формалары сызықтық тәуелсіз. Сонда
формалары сызықтық тәуелсіз. Сонда
![]() (1.1.13)
(1.1.13)
шекаралық шарттары
![]() (1.1.14)
(1.1.14)
шекаралық шарттарына түйіндес шекаралық шарт деп аталады. Егер шекаралық шарттар өзінің түйіндес шекаралық шарттарына эквивалент болса, онда шекаралық шарт өз-өзіне түйіндес деп аталады.
![]() дифференциалдық өрнегі мен (1.1.13) шекаралық шарттардан туындаған оператор
дифференциалдық өрнегі мен (1.1.13) шекаралық шарттардан туындаған оператор ![]() арқылы белгіленіп, бастапқы
арқылы белгіленіп, бастапқы ![]() операторына түйіндес деп аталады.
операторына түйіндес деп аталады. ![]() және
және ![]() операторлары үшін келесі теңдік орынды
операторлары үшін келесі теңдік орынды
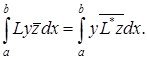
Егерде мынадай белгілеу еңгізсек
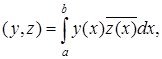
онда жоғарғы теңдігіміз мына түрге көшеді
![]()
![]() өз-өзіне түйіндес деп аталады, егерде
өз-өзіне түйіндес деп аталады, егерде ![]() болса.
болса.
Егер ![]() операторы
операторы ![]() операторының түйіндесі болса, онда
операторының түйіндесі болса, онда
![]() (1.1.15)
(1.1.15)
біртекті шекаралық есебі
![]() (1.1.16)
(1.1.16)
біртекті шекаралық есебіне түйіндес деп аталады.
1.2 Дифференциалдық оператордың меншікті мәндері мен меншікті функциялары
![]() саны
саны ![]() операторының меншікті мәні деп аталады, егерде
операторының меншікті мәні деп аталады, егерде ![]() операторының
операторының ![]() анықталу облысында
анықталу облысында ![]() функциясы табылып және келесі теңдік орындаса
функциясы табылып және келесі теңдік орындаса
![]() (1.2.1)
(1.2.1)
Бұл жердегі ![]() функциясы
функциясы ![]() операторының
операторының ![]() меншікті мәніне сәйкес меншікті функциясы деп аталады.
меншікті мәніне сәйкес меншікті функциясы деп аталады.
Айталық, ![]() дифференциалдық өрнегі мен
дифференциалдық өрнегі мен
![]() (1.2.2)
(1.2.2)
шекаралық шарттары ![]() операторын туындатсын.
операторын туындатсын. ![]() функциясы
функциясы ![]() операторының анықталу облысында жатуы керек болғандықтан, онда ол (1.2.2) шарттарын қанағаттандыруы керек. Оған қоса,
операторының анықталу облысында жатуы керек болғандықтан, онда ол (1.2.2) шарттарын қанағаттандыруы керек. Оған қоса, ![]() болғандықтан, (1.2.1)-ден
болғандықтан, (1.2.1)-ден
![]() (1.2.3)
(1.2.3)
Яғни, ![]() операторының меншікті мәні дегеніміз, біртекті шекаралық есеп
операторының меншікті мәні дегеніміз, біртекті шекаралық есеп
![]() (1.2.4)
(1.2.4)
тривиалды емес шешімге ие болған кездегі ![]() санын айтамыз, ал сол тривиалды емес шешімді
санын айтамыз, ал сол тривиалды емес шешімді ![]() меншікті мәніне сәйкес меншікті функция дейміз.
меншікті мәніне сәйкес меншікті функция дейміз.
Бір ![]() меншікті мәніне сәйкес бірнеше меншікті функциялардың сызықтық комбинациясыда сол
меншікті мәніне сәйкес бірнеше меншікті функциялардың сызықтық комбинациясыда сол ![]() меншікті мәніне сәйкес меншікті функция болады. Шынында да,
меншікті мәніне сәйкес меншікті функция болады. Шынында да,
![]() және
және ![]()
яғни, кез-келген ![]() тұрақтылары үшін келесі орынды
тұрақтылары үшін келесі орынды
![]()
Берілген ![]() үшін (1.2.3) біртекті теңдеу
үшін (1.2.3) біртекті теңдеу ![]() -нен көп емес сызықтық тәуелсіз шешімге ие болатындығынан, бір меншікті мәнге сәйкес барлық меншікті функциялар жиыны өлшемі
-нен көп емес сызықтық тәуелсіз шешімге ие болатындығынан, бір меншікті мәнге сәйкес барлық меншікті функциялар жиыны өлшемі ![]() ақырлы өлшемді кеңістік құратыны белгілі. Осы пайда болған кеңістіктің өлшемі, берілген
ақырлы өлшемді кеңістік құратыны белгілі. Осы пайда болған кеңістіктің өлшемі, берілген ![]() кезіндегі (1.2.4) шекаралық есептің сызықтық тәуелсіз шешімдерінің санын береді, және де бұл сан, меншікті мәннің еселігі деп аталады.
кезіндегі (1.2.4) шекаралық есептің сызықтық тәуелсіз шешімдерінің санын береді, және де бұл сан, меншікті мәннің еселігі деп аталады.
Меншікті мәндерді анықтайтын шарттарды табайық. Айталық,
![]() (1.2.5)
(1.2.5)
(1.2.3) дифференциалдық теңдеуінің іргелі шешімдер жүйесі болсын, олар келесідей бастапқы шарттарды қанағаттандырсын:
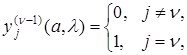 (1.2.6)
(1.2.6)
бұл жердегі![]() Сызықтық дифференциалдық теңдеулердің шешімі туралы жалпы теоремалардан,
Сызықтық дифференциалдық теңдеулердің шешімі туралы жалпы теоремалардан, ![]() аралығындағы кез-келген бекітілген
аралығындағы кез-келген бекітілген ![]() үшін (1.2.5) функциялар бүтін аналитикалық функциялар болатын белгілі. Жоғарыда айтқанымыздай, (1.2.4) шекаралық есептің тривиалдық емес шешімі болады, сонда және тек сонда, егерде
үшін (1.2.5) функциялар бүтін аналитикалық функциялар болатын белгілі. Жоғарыда айтқанымыздай, (1.2.4) шекаралық есептің тривиалдық емес шешімі болады, сонда және тек сонда, егерде
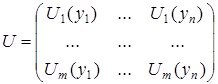
матрицасының рангы ![]()
![]() -нен кіші болса. Егер
-нен кіші болса. Егер ![]() болса, онда
болса, онда ![]() , яғни бұл жағдайда (1.2.4) шекаралық есеп кез-келген
, яғни бұл жағдайда (1.2.4) шекаралық есеп кез-келген ![]() үшін тривиалды емес шешімге ие болады. Демек,
үшін тривиалды емес шешімге ие болады. Демек, ![]() жағдайында
жағдайында ![]() -ның кез-келген мәні меншікті мән болады.
-ның кез-келген мәні меншікті мән болады.
Егер ![]() болса, онда онда
болса, онда онда ![]() матрицасының рангы
матрицасының рангы ![]() -нан кіші болады, сонда және тек сонда, егер
-нан кіші болады, сонда және тек сонда, егер ![]() матрицасының
матрицасының ![]() -ші ретті анықтауыштарының барлығы нөлге тең болса. Бірақ, ол анықтауыштар
-ші ретті анықтауыштарының барлығы нөлге тең болса. Бірақ, ол анықтауыштар ![]() -дан тәуелді аналитикалық функциялар болғандықтан тек келесідей ғана жағдайлар болуы мүмкін:
-дан тәуелді аналитикалық функциялар болғандықтан тек келесідей ғана жағдайлар болуы мүмкін:
1. ![]() матрицасының
матрицасының ![]() -ші ретті анықтауыштарының барлығы нөлге тепе тең. Бұл жағдай да
-ші ретті анықтауыштарының барлығы нөлге тепе тең. Бұл жағдай да ![]() -ның кез-келген мәні меншікті болып қала береді.
-ның кез-келген мәні меншікті болып қала береді.
2. ![]() матрицасының қандай да бір
матрицасының қандай да бір ![]() -ші ретті анықтауышы нөлге тепе тең емес. Бұл жағдай да тек осы анықтауыштың, қалған
-ші ретті анықтауышы нөлге тепе тең емес. Бұл жағдай да тек осы анықтауыштың, қалған ![]() -ші ретті анықтауыштарды да нөлге айналдыратын, түбірлері ғана меншікті мән болады.
-ші ретті анықтауыштарды да нөлге айналдыратын, түбірлері ғана меншікті мән болады.
Бірақ, нөлге тепе тең емес бүтін функцияның саналымдыдан артық емес түбірлері ғана болады (мүлде болмауыда мүмкін), және олардың ақырлы шектік нүктесі жоқ болады. Сәйкесінше, 2-ші жағдайда, ![]() операторы, ақырлы шектік нүктесі жоқ болатын, саналымдыдан аспайтын меншікті мәнге ие бола алады (олар мүлде жоқ болуыда мүмкін). Бұл екі жағдайды біріктіріп келесіні алса болады. Кез-келген дифференциалдық
операторы, ақырлы шектік нүктесі жоқ болатын, саналымдыдан аспайтын меншікті мәнге ие бола алады (олар мүлде жоқ болуыда мүмкін). Бұл екі жағдайды біріктіріп келесіні алса болады. Кез-келген дифференциалдық ![]() операторы үшін тек келесі екі жағдай ғана болуы мүмкін:
операторы үшін тек келесі екі жағдай ғана болуы мүмкін:
1. Кез-келген ![]() саны
саны ![]() операторының меншікті мәні болады.
операторының меншікті мәні болады.
2. ![]() операторының меншікті мәндер жиыны саналымдыдан аспайды (жеке жағдай да, бос жиын болуыда мүмкін) және ақырлы шектік нүктесі жоқ.
операторының меншікті мәндер жиыны саналымдыдан аспайды (жеке жағдай да, бос жиын болуыда мүмкін) және ақырлы шектік нүктесі жоқ.
Көптеген қызығушылықты ![]() жағдай тудырады. Алдағы уақытта, егерде бұл жайлы қосымша айтылмайтын болса, онда біз
жағдай тудырады. Алдағы уақытта, егерде бұл жайлы қосымша айтылмайтын болса, онда біз ![]() жағдайын қарастырамыз.
жағдайын қарастырамыз.
Айталық,
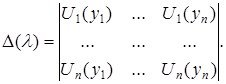 (1.2.7)
(1.2.7)
Алдыңғы айтқандарымыз бойынша ![]() -функциясы
-функциясы ![]() -дан тәуелді бүтін аналитикалық функция. Бұл функция
-дан тәуелді бүтін аналитикалық функция. Бұл функция ![]() операторының және де
операторының және де ![]() шекаралық есебінің мінездемелік анықтауышы деп аталады. Және де келесі тұжырым дұрыс:
шекаралық есебінің мінездемелік анықтауышы деп аталады. Және де келесі тұжырым дұрыс: ![]() операторының меншікті мәндері дегеніміз ол
операторының меншікті мәндері дегеніміз ол ![]() функциясының түбірлері болып табылады. Егер
функциясының түбірлері болып табылады. Егер ![]() функциясы нөлге тепе теі болса, онда кез-келген
функциясы нөлге тепе теі болса, онда кез-келген ![]() саны
саны ![]() операторының меншікті мәні болады. Ал егерде
операторының меншікті мәні болады. Ал егерде ![]() функциясы нөлге тепе тең болмаса, онда
функциясы нөлге тепе тең болмаса, онда ![]() операторы саналымдыдан аспайтын меншікті мәндер жиынына ие болады, және олардың ақырлы шектік нүктелері жоқ болады. Дербес жағдайда,
операторы саналымдыдан аспайтын меншікті мәндер жиынына ие болады, және олардың ақырлы шектік нүктелері жоқ болады. Дербес жағдайда, ![]() функциясының түбірлері жоқ болса, онда
функциясының түбірлері жоқ болса, онда ![]() операторының меншікті мәні жоқ болады.
операторының меншікті мәні жоқ болады.
Егерде ![]()
![]() функциясының еселігі
функциясының еселігі ![]() -ға тең түбірі болса, онда
-ға тең түбірі болса, онда ![]()
![]() операторының еселігі
операторының еселігі ![]() -дан аспайтын меншікті мәні болады. Егерде
-дан аспайтын меншікті мәні болады. Егерде ![]()
![]() функциясының жай түбірі болатын болса, онда
функциясының жай түбірі болатын болса, онда ![]() меншікті мәнінің еселігі бірге тең.
меншікті мәнінің еселігі бірге тең.
Меншікті мән табуға байланысты келесідей мысал қарастырайық:
1. ![]()
Бұл дифференциалдық теңдеудің жалпы шешімі:
![]()
түрінде болады. Бұл шешімді шекаралық шарттарға қойып, меншікті мән
![]()
болатынына оңай көз жеткізсе болады. ![]() жағдайында
жағдайында ![]() меншікті мәніне сызықтық тәуелсіз екі меншікті функция сәйкес келеді
меншікті мәніне сызықтық тәуелсіз екі меншікті функция сәйкес келеді
![]()
сәйкесінше, ![]() жаңдайында
жаңдайында ![]() меншікті мәні екі еселі. Ал
меншікті мәні екі еселі. Ал ![]() жағдайында
жағдайында ![]() меншікті мәніне тұрақтыға көбейту дәлдігімен тек бір ғана меншікті функция сәйкес келеді
меншікті мәніне тұрақтыға көбейту дәлдігімен тек бір ғана меншікті функция сәйкес келеді ![]() , демек бұл меншікті мән жай болады.
, демек бұл меншікті мән жай болады.
Енді, оператор мен оған түйіндес оператордың меншікті мәндері мен меншікті функциялары арасындағы қатынастарды көрсетейік.
Теорема 1.2.1. Егерде ![]() саны
саны ![]() операторының еселігі
операторының еселігі ![]() -ға тең меншікті мәні болса, онда
-ға тең меншікті мәні болса, онда ![]() саны
саны ![]() операторының дәл сол еселіктегі меншікті мәні болады.
операторының дәл сол еселіктегі меншікті мәні болады.
Дәлелдеуі. Айталық, ![]() операторы
операторы ![]() дифференциалдық өрнегі мен келесі шекаралық шарттардын туындасын
дифференциалдық өрнегі мен келесі шекаралық шарттардын туындасын
![]()
ал ![]() операторы
операторы ![]() дифференциалдық өрнегі мен
дифференциалдық өрнегі мен
![]()
шекаралық шарттарынан туындасын.
Және де
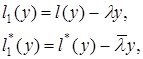
болсын. Егер де ![]() саны
саны ![]() операторының еселігі
операторының еселігі ![]() -ға тең меншікті мәні болса, онда
-ға тең меншікті мәні болса, онда
![]()
шекаралық есебінің ![]() сызықтық тәуелсіз шешімі бар болады, бұдан
сызықтық тәуелсіз шешімі бар болады, бұдан
![]()
шекаралық есебінің де ![]() сызықтық тәуелсіз шешімі бар екені белгілі[NAIMARK]. Ал бұдан
сызықтық тәуелсіз шешімі бар екені белгілі[NAIMARK]. Ал бұдан ![]() саны
саны ![]() операторының еселігі
операторының еселігі ![]() -ға тең меншікті мәні екені белгілі. Теорема дәлелденді.
-ға тең меншікті мәні екені белгілі. Теорема дәлелденді.
Екі ![]() және
және ![]() функцияларын ортогонал деп аталады, егерде
функцияларын ортогонал деп аталады, егерде ![]() болса.
болса.
Теорема 1.2.2. ![]() операторы мен
операторы мен ![]() операторының сәйкесінше
операторының сәйкесінше ![]() мен
мен ![]() меншікті мәндеріне сәйкес меншікті функциялары ортогонал болады, егерде
меншікті мәндеріне сәйкес меншікті функциялары ортогонал болады, егерде ![]() болса.
болса.
Дәлелдеуі. Айталық, ![]() функциясы
функциясы ![]() операторының
операторының ![]() меншікті мәніне сәйкес меншікті функциясы, ал
меншікті мәніне сәйкес меншікті функциясы, ал ![]() функциясы
функциясы ![]() операторының
операторының ![]() меншікті мәніне сәйкес меншікті функциясы болсын. Демек,
меншікті мәніне сәйкес меншікті функциясы болсын. Демек,
![]() және
және ![]()
Бұдан
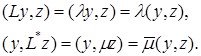
Бірақ бізде операторлар түйіндес болғандықтан, ![]() екені белгілі, демек
екені белгілі, демек ![]() ал бізде
ал бізде ![]() болғандықтан
болғандықтан ![]() екені шығады.
екені шығады.
Теорема дәлелденді.
Енді өз – өзіне түйіндес оператордың меншікті мәні мен меншікті функциясы жайлы айтатын болсақ.
Теорема 1.2.3. Өз – өзіне түйіндес оператордың барлық меншікті мәндері нақты болады.
Дәлелдеуі. Егерде ![]() өз – өзіне түйіндес оператор болатын болса, онда
өз – өзіне түйіндес оператор болатын болса, онда ![]() екені айқын, ал жеке жағдайда
екені айқын, ал жеке жағдайда ![]() екені де дұрыс. Ал басқа жағынан
екені де дұрыс. Ал басқа жағынан ![]() , сәйкесінше
, сәйкесінше ![]() нақты сан екені шығады.
нақты сан екені шығады.
Енді, айталық, ![]() саны
саны ![]() операторының меншікті мәні болсын, ал
операторының меншікті мәні болсын, ал ![]() сол меншікті мәнге сәйкес меншікті функция болсын. Онда
сол меншікті мәнге сәйкес меншікті функция болсын. Онда ![]() теңдігінен
теңдігінен ![]() екені шығады. Ал
екені шығады. Ал ![]() және
және ![]() нақты болғандықтан
нақты болғандықтан
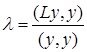
нақты сан екені шығады. Теорема дәлелденді.
Жоғарыдағы 1.2.2 және 1.2.3 теоремалардан келесі салдарды алса болады.
Салдар. Өз – өзіне түйіндес оператордың әр түрлі меншікті мәндерге сәйкес келетін меншікті функциялары ортогонал болады.
1.3 ![]() -ның үлкен мәндеріндегі меншікті мәндер мен меншікті функциялардың асимптотикасы.
-ның үлкен мәндеріндегі меншікті мәндер мен меншікті функциялардың асимптотикасы.
![]() -ның үлкен мәндерінде дифференциалдық оператордың меншікті мәндері мен меншікті функцияларының формулаларын жуықтап беруге болады. Бұл формулалар өздігінен қызығушылық тудыратынынан басқа, дифференциалдық операторлар теориясында кең қолданысқа ие. Жоғарыда берілген операторлар үшін бұл формулалар ең қарапайым жағдай
-ның үлкен мәндерінде дифференциалдық оператордың меншікті мәндері мен меншікті функцияларының формулаларын жуықтап беруге болады. Бұл формулалар өздігінен қызығушылық тудыратынынан басқа, дифференциалдық операторлар теориясында кең қолданысқа ие. Жоғарыда берілген операторлар үшін бұл формулалар ең қарапайым жағдай 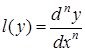
операторы жағдайымен бірдей екен.
Асипмтотикалық формулаларды алмас бұрын, ![]() теңдеуінің шешімінің
теңдеуінің шешімінің ![]() - ның үлкен кездеріндегі түрін біліп алғанымыз жөн. Сосын алынған шешімді
- ның үлкен кездеріндегі түрін біліп алғанымыз жөн. Сосын алынған шешімді ![]() теңдеуіне қойып, меншікті мән табылатын өрнек аламыз.
теңдеуіне қойып, меншікті мән табылатын өрнек аламыз.
Айталық, ![]() болсын онда,
болсын онда, ![]() теңдеуіміз келесі түрде жазылады
теңдеуіміз келесі түрде жазылады
![]() (1.3.1)
(1.3.1)
немесе ашып жазатын болсақ
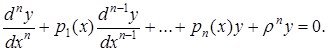 (1.3.2)
(1.3.2)
Жалпылықты бұзбай, ![]() деп санасақ болады, өйткені егерде
деп санасақ болады, өйткені егерде ![]() болатын болса,
болатын болса,
![]()
алмастыруын жасау арқылы, дәл сол ![]() мәні сақталатын, келесі түрдегі теңдеуге келе аламыз
мәні сақталатын, келесі түрдегі теңдеуге келе аламыз
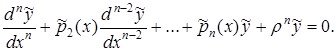
Және де ![]() функцияларыда
функцияларыда ![]() аралығында үзіліссіз функциялар болып қала береді. Келесі
аралығында үзіліссіз функциялар болып қала береді. Келесі ![]() аралығының орнына
аралығының орнына ![]() аралығын қарастыра берсе болады, себебі
аралығын қарастыра берсе болады, себебі ![]() өрнегі арқылы екі аралық арасында бірге бір сәйкестік қойсақ болады.
өрнегі арқылы екі аралық арасында бірге бір сәйкестік қойсақ болады.
Барлық ![]() -комплекс кеңістігін төмендегі теңсіздікпен анықталатын
-комплекс кеңістігін төмендегі теңсіздікпен анықталатын ![]() секторге бөлейік және де оларды
секторге бөлейік және де оларды ![]() арқылы белгілейік:
арқылы белгілейік:
![]()
Және де ![]() арқылы
арқылы ![]() -дің
-дің ![]() -ші ретті түбірлерін белгілейік. Келесідей дәлелдеусіз тұжырымды берейік: Кез – келген
-ші ретті түбірлерін белгілейік. Келесідей дәлелдеусіз тұжырымды берейік: Кез – келген ![]() секторы және кез – келген
секторы және кез – келген ![]() нүктелері үшін
нүктелері үшін ![]() сандарының төмендегі теңсіздік орындалатындай орналасуы табылады:
сандарының төмендегі теңсіздік орындалатындай орналасуы табылады:
![]()
Енді нормаланған шекаралық шарттарды қарастырайық. Жоғарыдағы дифференциалдық оператор үшін анықталған келесідей сызықтық формалар берілсін ![]()
![]() санын
санын ![]() формасының реті деп атайық, егерде бұл формада
формасының реті деп атайық, егерде бұл формада ![]() немесе
немесе ![]() бірі бар болып, ал
бірі бар болып, ал ![]() нөмірлері үшін
нөмірлері үшін ![]() немесе
немесе ![]() элементтерінің біреуіде жатпаса. Реті
элементтерінің біреуіде жатпаса. Реті ![]() -ге тең
-ге тең ![]() формасын қарастырайқ, егерде ондай форма бар болса. Керек жағдай да, біз форманы басқа формалардың сызықтық комбинацияларын қою арқылы реті
формасын қарастырайқ, егерде ондай форма бар болса. Керек жағдай да, біз форманы басқа формалардың сызықтық комбинацияларын қою арқылы реті ![]() -ге тең шекаралық шарттардың санын 2-ден аспайтындай етуімізге болады. Сәйкесінше қалған формалардың реті
-ге тең шекаралық шарттардың санын 2-ден аспайтындай етуімізге болады. Сәйкесінше қалған формалардың реті ![]() -ден аспайды. Дәл осылай істей беру арқылы реті бірдей шекаралық шарттардың санын минимумға келтіреміз. Бұл айтылған әдіс шекаралық шарттарды нормалау әдісі деп аталады, ал пайда болған шекаралық шарттарды нормаланған шекаралық шарттар деп атаймыз. Көрсетілген әдіс орындалғаннан кейінгі алынған шекаралық шарттар, яғни нормаланған шекаралық шарттар келесідей түрде болуы айқын:
-ден аспайды. Дәл осылай істей беру арқылы реті бірдей шекаралық шарттардың санын минимумға келтіреміз. Бұл айтылған әдіс шекаралық шарттарды нормалау әдісі деп аталады, ал пайда болған шекаралық шарттарды нормаланған шекаралық шарттар деп атаймыз. Көрсетілген әдіс орындалғаннан кейінгі алынған шекаралық шарттар, яғни нормаланған шекаралық шарттар келесідей түрде болуы айқын:
![]() (1.3.3)
(1.3.3)
бұл жердегі
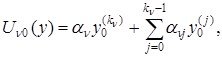 (1.3.4)
(1.3.4)
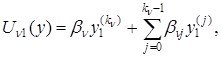 (1.3.5)
(1.3.5)
![]()
және де әрбір ![]() саны үшін
саны үшін ![]() сандарының біреуі нөлден өзгеше.
сандарының біреуі нөлден өзгеше.
Бекітілген ![]() облысын қарастырайық, жәнеде
облысын қарастырайық, жәнеде ![]() арқылы
арқылы ![]() үшін келесі шарт орындалатындай нөмірлеп шығайық
үшін келесі шарт орындалатындай нөмірлеп шығайық
![]()
Алдағы уақытта бізге регуляр шекаралық шарттар классын бөліп алу ыңғайлы болады. Бұл класс ![]() жұп немесе тақ болуына байланысты, екі түрлі анықталады.
жұп немесе тақ болуына байланысты, екі түрлі анықталады.
1. ![]() тақ болса, яғни
тақ болса, яғни ![]() (1.3.3)-ші нормаланған шекаралық шарттар регуляр деп аталады, егерде төмендегі теңдікпен анықталған
(1.3.3)-ші нормаланған шекаралық шарттар регуляр деп аталады, егерде төмендегі теңдікпен анықталған ![]() сандары нөлден өзгеше болса
сандары нөлден өзгеше болса
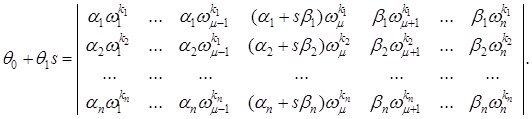
2. ![]() жұп болса, яғни
жұп болса, яғни ![]() (1.3.3)-ші нормаланған шекаралық шарттар регуляр деп аталады, егерде төмендегі теңдікпен анықталған
(1.3.3)-ші нормаланған шекаралық шарттар регуляр деп аталады, егерде төмендегі теңдікпен анықталған ![]() сандары нөлден өзгеше болса
сандары нөлден өзгеше болса
![]()
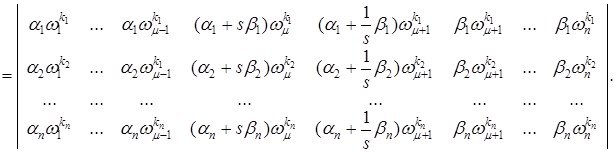
Бұл берілген регуляр шекаралық шарттардың анықтамасы ![]() сандарын нөмірлеуге қажет болған
сандарын нөмірлеуге қажет болған ![]() облысын таңдауға тәуелсіз.
облысын таңдауға тәуелсіз.
Енді осы айтылған регуляр шекаралық шарттарға біраз мысалдар қарастырайық:
1. ![]() жұп жағдайындағы Штурм тектес шеаралық шарттар. Бұл шекаралық шарттар келесідей түрде болады:
жұп жағдайындағы Штурм тектес шеаралық шарттар. Бұл шекаралық шарттар келесідей түрде болады:
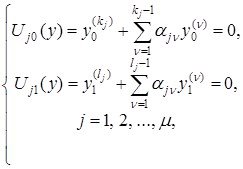
бұл жердегі
![]()
байқағанымыздай шекаралық шарттардың жартысы ![]() функциясының
функциясының ![]() нүктесіндегі мәндерін, ал жартысы
нүктесіндегі мәндерін, ал жартысы ![]() нүктесіндегі мәндерді қамтиды. Бұл жағдайда
нүктесіндегі мәндерді қамтиды. Бұл жағдайда
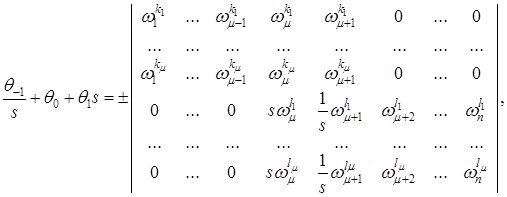
сәйкесінше,
![]()
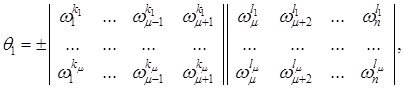 (1.3.6)
(1.3.6)
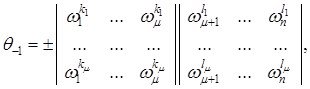 (1.3.7)
(1.3.7)
(1.3.6) және (1.3.7) формулаларындағы барлық анықтауыштар нөлден өзгеше, сол себепті Штурм тектес шекаралық шарттар регуляр екені шығады. ![]() болғандықтан, Штурм тектес шекаралық шарттар
болғандықтан, Штурм тектес шекаралық шарттар ![]() мағынасындағы күшейтілген регуляр екені шығады.
мағынасындағы күшейтілген регуляр екені шығады.
2. Периодты шекаралық шарттар регуляр. Бұл шарттар келесідей түрдегі шекаралық шарттар
![]()
Шыныменде, ![]() жағдайында
жағдайында
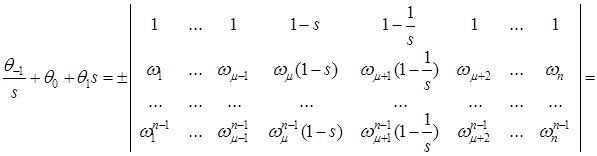
![]()
бұл жердегі ![]() -
- ![]() сандарының Вандермонд анықтауышы және сәйкесінше
сандарының Вандермонд анықтауышы және сәйкесінше ![]() Сол себепті,
Сол себепті,
![]()
демек, шекаралық шарттар регуляр болады. Дәл осылай ![]() тақ жағдайында да регуляр екенін көрсетуге болады.
тақ жағдайында да регуляр екенін көрсетуге болады.
3. ![]() жағдайындағы жалпы шекаралық шарттарды қарастырайық. Бұл жағдай да шекаралық шарттар келесі түрде болады
жағдайындағы жалпы шекаралық шарттарды қарастырайық. Бұл жағдай да шекаралық шарттар келесі түрде болады
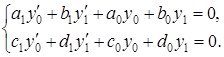
Келесі жағдайларда қарастырайық.
1) ![]() Онда жоғарыдағы шекаралық шарттарды
Онда жоғарыдағы шекаралық шарттарды ![]() белгісіздеріне қатысты шешіп келесідей түрге әкелеміз
белгісіздеріне қатысты шешіп келесідей түрге әкелеміз
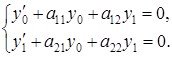
Бұл жағдай да
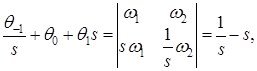
сәйкесінше, ![]() демек шекаралық шарттар регуляр.
демек шекаралық шарттар регуляр.
2) ![]() Бұл жағдайда шекаралық шарттарды келесі түрге келтіруге болады
Бұл жағдайда шекаралық шарттарды келесі түрге келтіруге болады

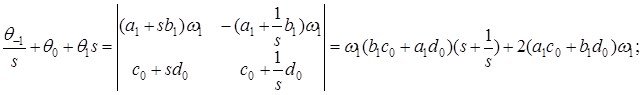
Демек, шекаралық шарттар бұл жағдайда регуляр болуы үшін ![]() болуы керек.
болуы керек.
3) ![]() Шекаралық шарттардағы формалар сызықтық тәуелсіз болуы керек болғандықтан
Шекаралық шарттардағы формалар сызықтық тәуелсіз болуы керек болғандықтан ![]() болуы керек, ал бұл келесі шекаралық шарттармен эквивалент
болуы керек, ал бұл келесі шекаралық шарттармен эквивалент
![]()
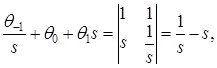
демек, шекаралық шарттар регуляр болады. Жоғарыда алынған жағдайлардың барлығын бірге қосып жазатын болсақ, келесідей шарттар аламыз:
Екінші ретті шекаралық шарттар келесі жағдайларда регуляр болады:
1) ![]()
2) ![]()
3) ![]()
Регуляр шекаралық шарттардың күшейтілген регуляр және күшейтілген емес регуляр деген екі классқа бөлсек болады. Регулярлық шекаралық шарттар күшейтілген регуляр деп аталады, егерде ![]() болса. Сызықтық жай дифференциалдық оператордың меншікті мәндерінің асимптотикасы, осы анықталған күшейтілген регуляр, күшейтілген емес регуляр шекаралық шарттар жағдайларында әр – түрлі анықталады. Келесідей теореманы дәлелдеусіз берейік, дәлелдеуін [1] кітабынан қарасаңыз болады.
болса. Сызықтық жай дифференциалдық оператордың меншікті мәндерінің асимптотикасы, осы анықталған күшейтілген регуляр, күшейтілген емес регуляр шекаралық шарттар жағдайларында әр – түрлі анықталады. Келесідей теореманы дәлелдеусіз берейік, дәлелдеуін [1] кітабынан қарасаңыз болады.
Теорема 1.3.1. Регуляр шекаралық шарттардан туындаған, ![]() интервалында анықталған
интервалында анықталған ![]() -ші ретті дифференциалдық оператордың меншікті мәндері екі шексіз сериядан
-ші ретті дифференциалдық оператордың меншікті мәндері екі шексіз сериядан ![]() тұрады,
тұрады, ![]() - қандайда бір бүтін сан.
- қандайда бір бүтін сан.
![]() -тақ жағдайы,
-тақ жағдайы, ![]()
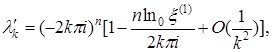 (1.3.8)
(1.3.8)
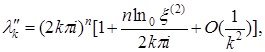 (1.3.9)
(1.3.9)
Ал ![]() -тақ, бірақ
-тақ, бірақ ![]() болғанда
болғанда
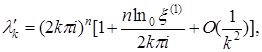 (1.3.10)
(1.3.10)
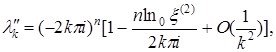 (1.3.11)
(1.3.11)
бұл жердегі, ![]() сандары
сандары ![]() облысына сәйкес,
облысына сәйкес, ![]() жұп немесе тақ жағдайларындағы
жұп немесе тақ жағдайларындағы ![]() теңдеулерінің түбірлері.
теңдеулерінің түбірлері.
![]() -жұп жағдайы,
-жұп жағдайы, ![]() және
және ![]()
![]() (1.3.12)
(1.3.12)
![]() (1.3.13)
(1.3.13)
бұл жердегі, ![]() сандары
сандары
![]() (1.3.14)
(1.3.14)
теңдеуінің, ![]() облысына сәйкес келетін түбірлері. Ал формуладығы қосу алу белгілері,
облысына сәйкес келетін түбірлері. Ал формуладығы қосу алу белгілері, ![]() -дың сәйкесінше тақ жұп болуына байланысты.
-дың сәйкесінше тақ жұп болуына байланысты.
Ал ![]() -жұп,
-жұп, ![]() және
және ![]()
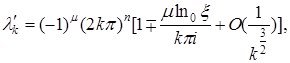 (1.3.15)
(1.3.15)
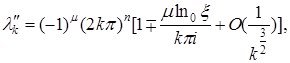 (1.3.16)
(1.3.16)
бұл жердегі, ![]()
![]() облысына сәйкес келетін (1.3.14) теңдеудің еселі түбірі. Ал формуладығы қосу алу белгілері,
облысына сәйкес келетін (1.3.14) теңдеудің еселі түбірі. Ал формуладығы қосу алу белгілері, ![]() -дың сәйкесінше тақ жұп болуына байланысты.
-дың сәйкесінше тақ жұп болуына байланысты.
Алғашқы үш жағдайда белгілі бір нөмірден бастап барлық меншікті мәндер қарапайым болады, ал төртінші жағдайда белгілі бір нөмірден бастап меншікті мәндері қарапайым немесе екі еселі.
Енді алдағы уақытта регуляр шекаралық шарттардың әр түріне жеке тоқталып, төртінші ретті дифференциалдық оператор үшін регуляр, оның ішінде күшейтілген және күшейтілген емес шекаралық шарттарды бөліп алып. Сол әр шарттқа сәйкес дифференциалдық оператордың меншікті функцияларының асимптотикасын алып, олардың базис болу болмауын тексереміз.
Шекаралық шарттар күшейтілген регуляр болған жағдайда оператордың меншікті және қосалқы функциялары ![]() кеңістігінде Рисс базисін құратыны белгілі. Бұл айтылғанды ең алғаш В.П. Михайлов көрсетті. Дәл осы нәтиже Кессельман Г.М. жұмыстарында, және Данфорд Н. мен Шварц Т. монографиясында бар. Бұл жұмыстардың барлығында да, дәлелдеу оператор мен оның түйіндес операторының нормаланған меншікті және қосалқы функциялар жүйесінің бесселдік екендігіне әкелінді.
кеңістігінде Рисс базисін құратыны белгілі. Бұл айтылғанды ең алғаш В.П. Михайлов көрсетті. Дәл осы нәтиже Кессельман Г.М. жұмыстарында, және Данфорд Н. мен Шварц Т. монографиясында бар. Бұл жұмыстардың барлығында да, дәлелдеу оператор мен оның түйіндес операторының нормаланған меншікті және қосалқы функциялар жүйесінің бесселдік екендігіне әкелінді.
Кессельман Г.М. жұмыстарында шекаралық шарттары регуляр бірақ күшейтілген емес регуляр болатын дифференциалдық оператордың меншікті және қосалқы функциялары базис құрмайтындай мысалдар көрсеткен. Себебі бұл жағдайларда оператор Данфорд Н. мағынасында спектральды болмайды, демек бұл жағдайда оператордың меншікті және қосалқы функциялары Рисс базисін құрмайтыны белгілі. Бұл жайтты, оператордың меншікті мәндері асимптотикалық жақын орналасқандығымен түсіндіруге болады, демек келесідей асимптотикаға ие
![]()
![]() болғанда. Соның ішінде жақын орналасқан меншікті мәндерге сәйкес меншікті функциялар бір біріне тең емес, бірақта арасындағы бұрыш нөлге ұмтылады. Дәл осындай жағдайларда оператордың меншікті және қосалқы функциялар жүйесі базис құрмайды.
болғанда. Соның ішінде жақын орналасқан меншікті мәндерге сәйкес меншікті функциялар бір біріне тең емес, бірақта арасындағы бұрыш нөлге ұмтылады. Дәл осындай жағдайларда оператордың меншікті және қосалқы функциялар жүйесі базис құрмайды.
Келесідей дифференциалдық өрнекпен
![]()
жалпы түрдегі шекаралық шарттардан туындаған
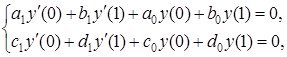
оператор қарастырайық. Жоғарыда айтқанымыздай шекаралық шарттар регуляр болады, егерде төмендегі үш шарттын біреуі орындалса:
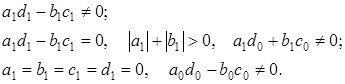
Ал регуляр шекаралық шарттар күшейтілген регуляр деп аталады, егерде бірінші немесе екінші шарттар орындалған жағдайда, және екінші жағдайда, егерде тағы қосымша келесідей шарт орындалса
![]()
Екінші ретті дифференциалдық операторлар үшін регуляр, бірақ күшейтілген регуляр емес шекаралық шарттардың келесідей ыңғайлы түрі бар [2]. Бұл жұмыста регуляр, бірақ күшейтілген емес регуляр шекаралық шарт келесі түрге келтіріледі
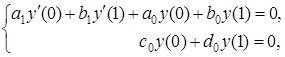
![]()
жәнеде келесі төрт шарттын біреуін қанағаттандырады:
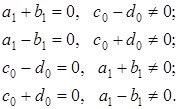
Екінші ретті дифференциалдық операторларға қарағанда төртінші ретті шекаралық шарттары күшейтілген емес регуляр болатын дифференциалдық операторлардың спектральдық теориясы азырақ дамыған. Бұған байланысты тек жекеленген жұмыстар ғана бар.[3,4] Бұл дипломдық жұмыста алдағы уақытта дәл осы шекаралық шарттар күшейтілген емес регуляр болатын төртінші ретті дифференциалдық операторлардың спектральдық қасиеттері зерттеледі.
Келесідей түрдегі дифференциалдық өрнекпен
![]() (1.3.17)
(1.3.17)
жалпы түрдегі шекаралық шарттардан
![]()
![]() (1.3.18)
(1.3.18)
туындаған дифференциалдық оператор қарастырайық, бұл жерде ![]() комплекс коэффициентті сызықтық тәуелсіз формалар. Осы берілген шекаралық шарттардың коэффициенттерінен құралған матрицаны
комплекс коэффициентті сызықтық тәуелсіз формалар. Осы берілген шекаралық шарттардың коэффициенттерінен құралған матрицаны ![]() арқылы белгілейік. Келесідей жеті жағдайда шекаралық шарттар күшейтілген емес регуляр болады:
арқылы белгілейік. Келесідей жеті жағдайда шекаралық шарттар күшейтілген емес регуляр болады:
 (1.3.19)
(1.3.19)
(1.3.19)-шы шекаралық шарттар регуляр болады, егерде ![]() күшейтілген емес регуляр болады, егерде
күшейтілген емес регуляр болады, егерде ![]()
 (1.3.20)
(1.3.20)
(1.3.20)-шы шекаралық шарттар регуляр болады, егерде ![]() күшейтілген емес регуляр болады, егерде
күшейтілген емес регуляр болады, егерде ![]()
 (1.3.21)
(1.3.21)
(1.3.21)-шы шекаралық шарттар регуляр болады, егерде ![]() күшейтілген емес регуляр болады, егерде
күшейтілген емес регуляр болады, егерде ![]()
 (1.3.22)
(1.3.22)
(1.3.22)-шы шекаралық шарттар регуляр болады, егерде ![]() күшейтілген емес регуляр болады, егерде
күшейтілген емес регуляр болады, егерде ![]()
 (1.3.23)
(1.3.23)
(1.3.23)-шы шекаралық шарттар регуляр болады, егерде ![]() күшейтілген емес регуляр болады, егерде
күшейтілген емес регуляр болады, егерде ![]()
 (1.3.24)
(1.3.24)
(1.3.24)-шы шекаралық шарттар регуляр болады, егерде ![]() күшейтілген емес регуляр болады, егерде
күшейтілген емес регуляр болады, егерде ![]()
Жәнеде күшейтілген емес регуляр болатын шекаралық шарттардың классы келесідей түрде:
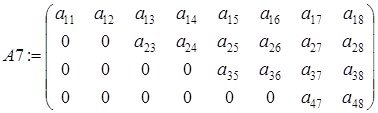 (1.3.25)
(1.3.25)
(1.3.24)-шы шекаралық шарттар регуляр болады, егерде ![]() күшейтілген емес регуляр болады, егерде келесі екі шарттын біреуі орындалса:
күшейтілген емес регуляр болады, егерде келесі екі шарттын біреуі орындалса:
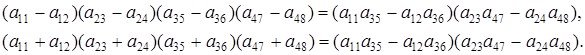
Енді осы берілген жағдайларды жеке қарастырайық. Бұл жердегі алғашқы алты жағдайдың спектральдық қасиеттері мен соларға байланысты теоремалар және олардың дәлелдеулері ұқсас, сол себепті тек бірінші жағдайға ғана тоқтала кетейік. Бірінші жағдайдың өзінде де бір дербес есепті дәлелдеуімен көрсетіп, жалпы түрде тек теореманы көрсете кетеміз.
Айталық, келесідей есепті қарастырайық
![]()
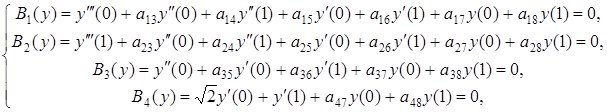
Бұл есеп бірінші классқа тиісті екені айқын, сәйкесінше шекаралық шарттары күшейтілген емес регуляр болады.
Лемма 1.3.2 Жоғарыда берілген барлық меншікті мәндері белгілі бір нөмірден бастап қарапайым жәнеде келесідей екі серия құрады ![]() бұл жердегі
бұл жердегі ![]() оң бүтін сан:
оң бүтін сан:
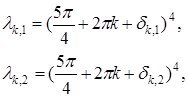
бұл жердегі 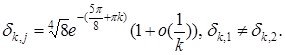
Дәлелдеуі. Дәлелдеуі берілген есептің характеристикалық анықтауышын есептеп, Руше теоремасын қолдануға сүйенеді. Сол себепті дәлелдеуіне тоқталмаймыз. Ал меншікті мәндер қарапайым болатынын ![]() екенін көрсету арқылы дәлелдеуге болады.
екенін көрсету арқылы дәлелдеуге болады.
Теорема 1.3.3 Жоғарыдағыесептің ![]() меншікті мәндеріне сәйкес меншікті функциялары келесідей түрде болады
меншікті мәндеріне сәйкес меншікті функциялары келесідей түрде болады
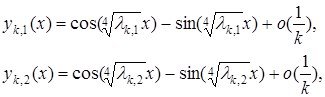
бұл жердегі ![]() жеткілікті үлкен сан.
жеткілікті үлкен сан.
Дәлелдеуі. Берілген теңдеуіміздің жалпы шешімі келесідей түрде жазылады
![]()
Осы жалпы шешімімізді шекаралық шарттарға қойсақ белгісіз тұрақтыларға байланысты жүйе аламыз
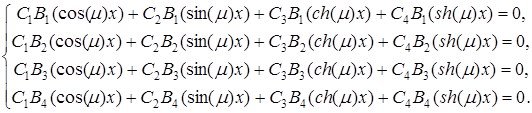
Бұл жүйені шешу барысында келесідей шешім аламыз
![]()
бұл жердегі
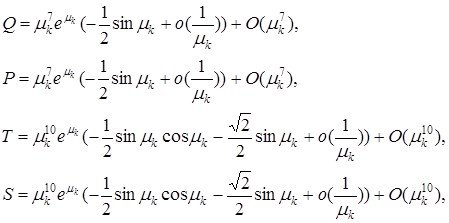
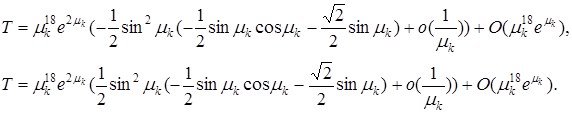
Демек,
Бұл алғандарымызды жалпы шешімге қойып жәнеде ![]() деп алсақ, теоремамыздың дәлелдеуі шығады.
деп алсақ, теоремамыздың дәлелдеуі шығады.
Теорема 1.3.4 Жоғарыдағы есептің ![]() меншікті мәндеріне сәйкес меншікті функцияларының жүйесі
меншікті мәндеріне сәйкес меншікті функцияларының жүйесі ![]()
![]() кеңістігінде базис құрмайды.
кеңістігінде базис құрмайды.
Дәлелдеуі. Келесідей скаляр көбейтінді қарастырайық
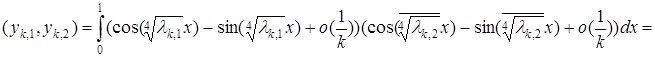
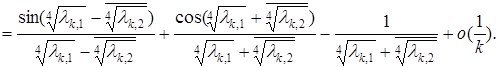
Бұл жерден Лемма 1.3.2-ның көмегі мен жеткілікті үлкен ![]() сандары үшін
сандары үшін ![]() екені айқын. [5] жұмысынның көмегімен бұл жүйе базис құрмайтынын көреміз.
екені айқын. [5] жұмысынның көмегімен бұл жүйе базис құрмайтынын көреміз.
Теорема дәлелденді.
Енді бірінші класстағы шекаралық шарттарды жалпы қарастырайтын болсақ, бізде шекаралық шарттар күшейтілген регуляр болуы үшін келесі шарттар орындалу керек:
![]()
Ал бұл екі шартты қанағаттандыратын коэффициенттердің жалпы шешімі келесі түрде
![]() немесе
немесе
![]()
бұл жердегі ![]() кез – келген комплекс сан (
кез – келген комплекс сан (![]() жағдайы
жағдайы ![]() болатын жағдайға түйіндес, ал жай дифференциалдық оператор мен оның спектральдық қасиеттері бірдей болғандықтан ол жағдайды қарамасақта болады). Яғни жалпы алынған шешімге байланысты жалпы есепке қатысты келесідей теорема 1.3.3-ке ұқсас теорема аламыз
болатын жағдайға түйіндес, ал жай дифференциалдық оператор мен оның спектральдық қасиеттері бірдей болғандықтан ол жағдайды қарамасақта болады). Яғни жалпы алынған шешімге байланысты жалпы есепке қатысты келесідей теорема 1.3.3-ке ұқсас теорема аламыз
Теорема 1.3.5 Жоғарыдағы жалпы есептің ![]() меншікті мәндеріне сәйкес меншікті функциялары келесідей түрде болады
меншікті мәндеріне сәйкес меншікті функциялары келесідей түрде болады
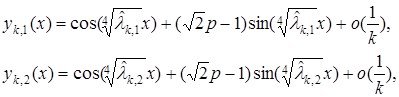
бұл жердегі ![]() жеткілікті үлкен сан.
жеткілікті үлкен сан.
Дәл теорема 1.3.4-ке ұқсас бұл алынған жұйемізде ![]() кеңістігінде базис құрмайтыны айқын [5].
кеңістігінде базис құрмайтыны айқын [5].
2 ЕКІНШІ РЕТТІ ДИФФЕРЕНЦИАЛДЫҚ ОПЕРАТОРДЫҢ ОЙЫЛҒАН КЕСІНДІДЕГІ БІРІНШІ РЕГУЛЯРИЗАЦИЯЛАНҒАН ІЗІ
2.1 Есептің қойылуы және нәтижелер
Келесідей функционалдық кеңістік еңгізейік ![]() , және де ол
, және де ол ![]() интервалының барлық дерлік жерінде анықталған
интервалының барлық дерлік жерінде анықталған ![]() және келесідей шарттарды қанағаттандыратын
және келесідей шарттарды қанағаттандыратын ![]() функциялар кеңістігі болсын, бұл жердегі
функциялар кеңістігі болсын, бұл жердегі ![]() -
- ![]() интервалының характеристикалық функциясы. Бұл берілген
интервалының характеристикалық функциясы. Бұл берілген ![]() кеңістігі
кеңістігі ![]() кеңістігіне тең болмайды, өйткені
кеңістігіне тең болмайды, өйткені 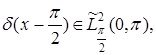 бірақ
бірақ 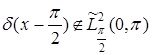 Бұл кеңістіктің нормасын келесідей түрде еңгізейік
Бұл кеңістіктің нормасын келесідей түрде еңгізейік
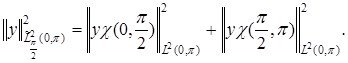
Осы берілген ![]() кеңістігінде келесідей дифференциалдық өрнекпен
кеңістігінде келесідей дифференциалдық өрнекпен
![]() (2.1.1)
(2.1.1)
төмендегі шекаралық шарттардан
![]() (2.1.2)
(2.1.2)
![]() (2.1.3)
(2.1.3)
![]() (2.1.4)
(2.1.4)
![]() (2.1.5)
(2.1.5)
туындаған ![]() операторының бірінші регуляризацияланған ізін зерттейміз.
операторының бірінші регуляризацияланған ізін зерттейміз.
Айтылып жатылған мағлұматтың толықтығы үшін ![]() операторының ақырлы ойылған кесіндідегі қисынды анықтамасын берейік.
операторының ақырлы ойылған кесіндідегі қисынды анықтамасын берейік. ![]() дифференциалдық өрнегін
дифференциалдық өрнегін ![]() және
және ![]() интервалдарының қиылысуында қарастырайық. Бұл айтылған дифференциалдық өрнекке төмендегідей анықталған
интервалдарының қиылысуында қарастырайық. Бұл айтылған дифференциалдық өрнекке төмендегідей анықталған ![]() максималды операторын сәйкес қояйық
максималды операторын сәйкес қояйық
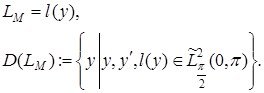
Яғни ![]() операторын осын берілген максималды оператордың тарылуы ретінде алсақ болады
операторын осын берілген максималды оператордың тарылуы ретінде алсақ болады
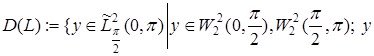
![]() қанағаттандырады
қанағаттандырады![]()
Регуляризацияланған іздер теориясының дамуына жол ашқан жұмыстар 1947-1952 И.М. Лифщиц жұмыстары болған. Регуляризацияланған іздердің формулалары физикалық мағынаға ие болған екен және де И.М. Лифщиц [6] өзі тапқан формулалар арқылы криссталлға бөгде қоспа қосу барысындағы оның бос энергегиясының өзгерісін анықтаған. ![]() кеңістігінде анықталған
кеңістігінде анықталған
![]() (2.1.6)
(2.1.6)
дифференциалдық өрнегі мен Дирихле шекаралық шарттарынан туындаған Штурм – Лиувилль операторы үшін, меншікті мәндерін ![]() арқылы белгілеп және жатық потенциал
арқылы белгілеп және жатық потенциал ![]() үшін келесідей классикалық бірінші регуляризацияланған іздің формуласы бар ([7]-[10]):
үшін келесідей классикалық бірінші регуляризацияланған іздің формуласы бар ([7]-[10]):
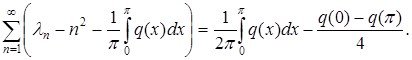
Бұл формула кез – келген, ![]() және
және ![]() нүктелеріндегі Фурбе қатары осы функцияның өзінің мәндеріне жинақталатын
нүктелеріндегі Фурбе қатары осы функцияның өзінің мәндеріне жинақталатын ![]() потенциалы үшін де сақталады екен [11].
потенциалы үшін де сақталады екен [11].
![]() жағдайында бірінші регуляризацияланған іздің формуласын В.А. Винокуров және В.А. Садовничий есептеген [12]. Олар кез – келген
жағдайында бірінші регуляризацияланған іздің формуласын В.А. Винокуров және В.А. Садовничий есептеген [12]. Олар кез – келген ![]() функциясы үшін
функциясы үшін
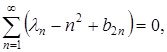
қатары жинақталатынын дәлелдеген. Бұл жердегі ![]() -
- ![]() кесіндісіндегі вариациясы шектелген функция, және де кесіндінің шеттерінде үзіліссіз.
кесіндісіндегі вариациясы шектелген функция, және де кесіндінің шеттерінде үзіліссіз.
[13] жұмыста, потенциалы ![]() болатын (2.1.6), (2.1.2), (2.1.5)-ші есептің бірінші регуляризацияланған ізі:
болатын (2.1.6), (2.1.2), (2.1.5)-ші есептің бірінші регуляризацияланған ізі:
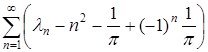
жинақталатыны және оның қосындысы ![]() екені көрсетілген. Бұл операторды [14] жұмыстағы жалпылама нәтижелерді қолданып анықтасада болады. Осындай түрдегі операторлардың басқада практикалық қолданыстарын [15] жұмыстан қараса болады.
екені көрсетілген. Бұл операторды [14] жұмыстағы жалпылама нәтижелерді қолданып анықтасада болады. Осындай түрдегі операторлардың басқада практикалық қолданыстарын [15] жұмыстан қараса болады.
Алдағы уақытта зерттелініп отырылған ![]() операторының бірінші регуляризацияланған ізі ретінде
операторының бірінші регуляризацияланған ізі ретінде ![]() болғандағы дербес қосындылардың шегін айтатын боламыз
болғандағы дербес қосындылардың шегін айтатын боламыз
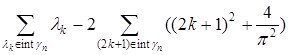 (2.1.7)
(2.1.7)
егерде қандайда бір шектелмеген өспелі ![]() контурларының тізбегі табылса.
контурларының тізбегі табылса. ![]() арқылы комплекс кеңістіктегі радиусы
арқылы комплекс кеңістіктегі радиусы ![]() болатын шеңберлерді белгілейік.
болатын шеңберлерді белгілейік.
Теорема 2.1.1. Айталық, ![]() - (2.1.1)-(2.1.5) есебіне сәйкес екінші ретті дифференциалдық оператор болсын. Онда
- (2.1.1)-(2.1.5) есебіне сәйкес екінші ретті дифференциалдық оператор болсын. Онда ![]() болғанда (2.1.7) дербес қосындыларының шегі бар және ол
болғанда (2.1.7) дербес қосындыларының шегі бар және ол ![]() болады.
болады.
2.2 Характеристикалық анықтауыш
Бұл бөлімде біз ![]() кеңістігінде анықталған кеңірек анықталған операторлар классының характеристикалық анықтауышын есептейміз, айталық, (2.1.1) дифференциалдық өрнекпен келесідей шекаралық шарттардан туындаған оператор қарастырайық
кеңістігінде анықталған кеңірек анықталған операторлар классының характеристикалық анықтауышын есептейміз, айталық, (2.1.1) дифференциалдық өрнекпен келесідей шекаралық шарттардан туындаған оператор қарастырайық
![]() (2.1.2)
(2.1.2)
![]() (2.2.1)
(2.2.1)
![]() (2.1.4)
(2.1.4)
![]() (2.1.5)
(2.1.5)
бұл жердегі ![]() .
. ![]() болғанда жоғарыдағы оператор шектелген қайтымды және жтим, что при
болғанда жоғарыдағы оператор шектелген қайтымды және жтим, что при ![]() оператор
оператор ![]() является ограниченно обратимым, барлық дерлік жерде үзіліссіз екені [16-17] жұмыстарынан белгілі.
является ограниченно обратимым, барлық дерлік жерде үзіліссіз екені [16-17] жұмыстарынан белгілі.
Егерде
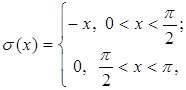 (2.2.2)
(2.2.2)
десек, онда бастапқы ![]() операторын аламыз.
операторын аламыз.
![]() жағдайында
жағдайында ![]() операторы төмендегі дифференциалдық өрнекпен Дирихле шекаралық шарттарынан туындаған Штурм – Лиувилль, операторына эквивалент екені [13] жұмыстан белгілі
операторы төмендегі дифференциалдық өрнекпен Дирихле шекаралық шарттарынан туындаған Штурм – Лиувилль, операторына эквивалент екені [13] жұмыстан белгілі
![]()
[18] жұмыста Лаплас операторының ойылған шеңбердегі қисынды шешілетін барлық шекаралық шарттар сипатталған. Ал [19] жұмыста Лаплас операторының ойылған облыстағы өз – өзіне түйіндес кеңейімдер сипатталған.
Алдағы атқарылатын жұмыстарда келесі лемма үлкен рөл атқарады.
Лемма 2.2.1 Осы бөлім басында берілген оператордың характеристикалық анықтауышы келесі формуламен анықталады:
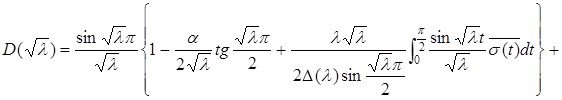
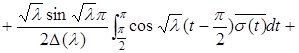
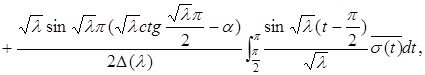 (2.2.3)
(2.2.3)
бұл жердегі 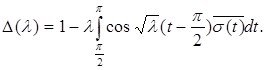
Дәлелдеуі. ![]() аралығында шешім келесідей түрде болады
аралығында шешім келесідей түрде болады 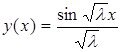 . (2.2.1) шартты ескере отырып, келесі теңдікті аламыз
. (2.2.1) шартты ескере отырып, келесі теңдікті аламыз
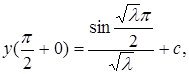
бұл жердегі 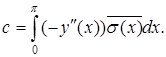 Енді (2.1.4) шарртты ескере отырып
Енді (2.1.4) шарртты ескере отырып
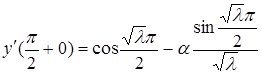
екені айқын. Сол себепті ![]() аралығында шешім келесідей түрде жазылады
аралығында шешім келесідей түрде жазылады
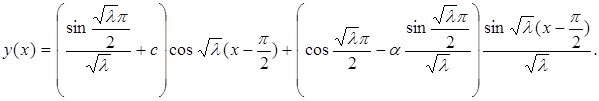
Енді с тұрақтысын анықтайық:
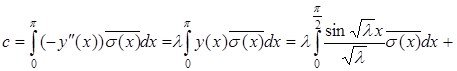
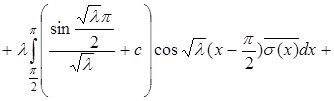
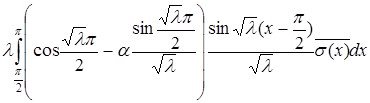
Яғни:
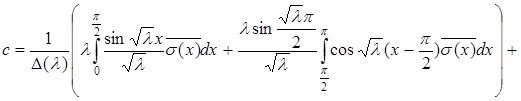
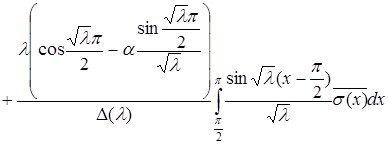
Бұдан алатынымыз
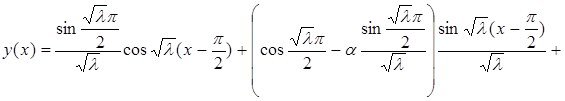
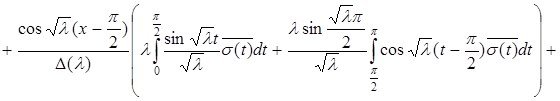
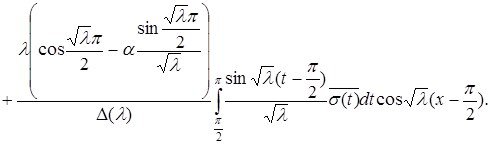
(2.1.5) шартты ескере отырып
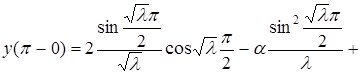
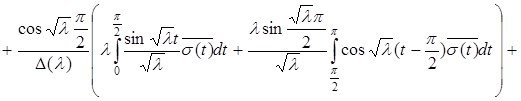
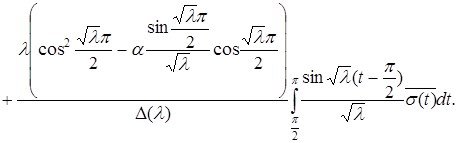
Соңғы алынған теңдіктен (2.2.3)-ші формула шығатыны айқын.
Лемма 2.2.1 дәлелденді.
2.3 Негізгі нәтиженің дәлелдеуі
Шекаралық функция ![]() (2.2.2) формуласы түрінде болғандықтан
(2.2.2) формуласы түрінде болғандықтан![]() екені айқын.
екені айқын.
Енді (2.2.2) теңдікті пайдаланып, (2.2.3)-ші формуланы келесідей түрге келтіреміз:
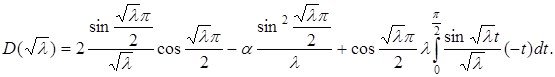
Ал Лагранж формуласы арқылы:
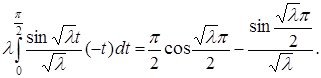 (2.3.1)
(2.3.1)
(2.3.1) теңдікті ескере отырып
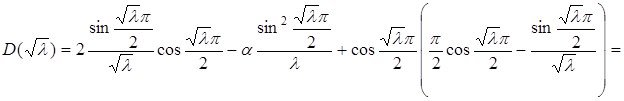
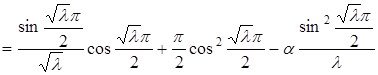
Айталық, ![]() болсын:
болсын:
![]() (2.3.2)
(2.3.2)
бұл жердегі
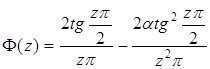
Байқағанымыздай, ![]() жұп функция, ал
жұп функция, ал ![]() функциясы
функциясы ![]() контурында қандайда бір тұрақтымен шенелген, жәнеде ол тұрақты
контурында қандайда бір тұрақтымен шенелген, жәнеде ол тұрақты ![]() -нан тәуелсіз, жәнеде
-нан тәуелсіз, жәнеде ![]() функциясы
функциясы ![]() -ның үлкен мәндерінде
-ның үлкен мәндерінде ![]() -да голоморфты.
-да голоморфты.
Лемма 2.3.1 ![]() болған кезде келесідей интегралдық теңдіктер орынды:
болған кезде келесідей интегралдық теңдіктер орынды:
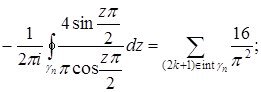
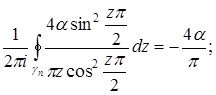
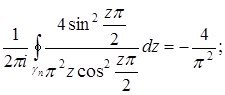
Дәлелдеуі. Бірінші интеграл ![]() нүктелерінде қарапайым полюсы болғандықтан:
нүктелерінде қарапайым полюсы болғандықтан:
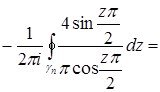
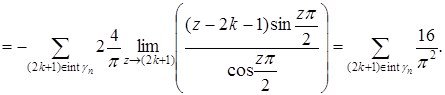
Енді екінші интегралды есептейік. Шыныменде ![]() болғанда
болғанда
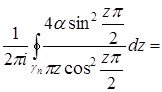
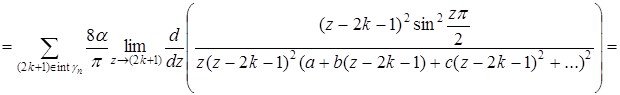
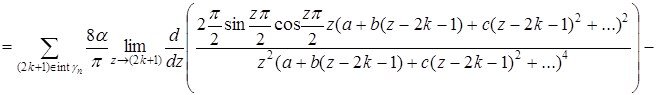
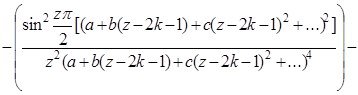
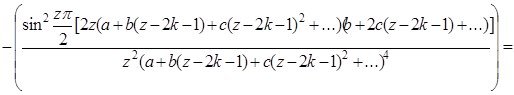
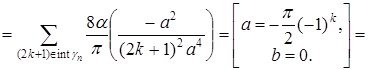
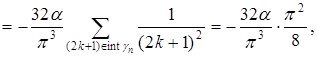
бұл жердегі a,b,c,... ![]() функциясының Тейлор коэффициенттері, жәнеде
функциясының Тейлор коэффициенттері, жәнеде 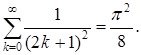
Енді екінші интегралды қолданып үшіншісін есептейік:
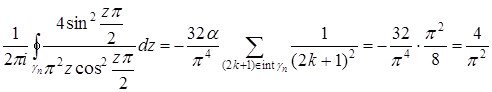
Лемма дәлелденді.
Теореманың дәлелдеуі. Теореманы дәлелдеу үшін Кошидің шегерімдер туралы теоремасын (2.3.2) теңдікке қолданайық
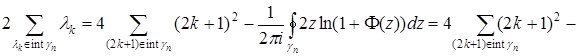
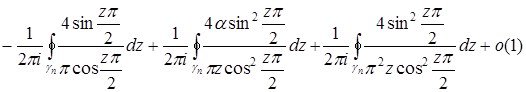
Ал Лемма 2.3.1-ден
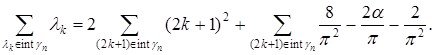 (2.3.3)
(2.3.3)
Ал бұл теңдіктен теореманың дәлелденгені көрініп тұр.
ҚОРЫТЫНДЫ
Төртінші ретті дифференциалдық оператордың біраз спектральдік қасиеттері зерттелді. Соның ішінде регуляр, бірақ күшейтілген емес шекаралық шарттардың жалпы түрі берілді. Айта кететіні алғашқы алынған алты жағдайдыі, бұдан бұрын алынған екінші ретті диференциалдық оператордағы күшейтілген емес регуляр шекаралық шарттардан айырмашылығы. Және сол алты жағдайдан туындаған оператордың меншікті мәндері мен меншікті функцияларының асимптотикасы алынды. Жәнеде меншікті функциялар жүйесі ![]() кеңістігінде базис құрмайтыны анықталды. Алдағы уақытта аз зерттелген жетінші жағдай тереңірек зерттеледі.
кеңістігінде базис құрмайтыны анықталды. Алдағы уақытта аз зерттелген жетінші жағдай тереңірек зерттеледі.
Екінші есеп ретінде ойылған кесіндіде анықталған екінші ретті дифференциалдық оператордың бірінші регуляризацияланған ізін есептеу болған. Бұл мақсатта толық ақталды деген сенімдемін. Өйткені бірінші регуляризациялаған із есептеліп ғана қоймай, бірінші регуляризацияланған із үшін осыған дейін белгілі классикалық Гельфанд – Левитан формуласына ұқсас формула алынды.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
1. Naimark, M.A: Lineinye differencialnye operatory (Linear Differential Operators) [in Russian]. Nauka. (Moskva). 2, (1969).
2. Orazov, I ,Sadybekov, MA: On a class of problems of determining the temperature and density of heat sources given initial and final temperature . Siberian Mathematical Journal. 53, (1), 146--151 (2012).
3. Kerimov, NB, Kaya, U: Some problems of spectral theory of fourth-order differential operators with regular boundary conditions. Arab J Math. 3, 49--61 (2014).
4. Menken, H: Accurate Asymptotic Formulas for Eigenvalues and Eigenfunctions of a Boundary-Value Problem of Fourth Order. Boundary Value Problems. 10, (1), 21 pages (2010).
5. Sadybekov, MA, Sarsenbi, AM: On a necessary condition for a system of normalized elements to be a basis in a Hilbert space [in Russian]. Vestn. Tomsk. Gos. Univ. Mat. Mekh. 13, (1), 44--46 (2013).
6. И.М. Лифшиц, Об одной задаче теории возмущений связанной с квантовой статистикой // УМН. 1952. Т.7. №1(47). С.171-180.
7. И.М. Гельфанд, Б.М. Левитан, Об одном простом тождестве для собственных значений дифференциального оператора второго порядка // Докл. АН СССР. 1953. Т.88. №4. С.593-596.
8. Л.А. Дикий, Об одной формуле Гельфанда-Левитана // УМН. 1953. Т.8. №2. С.119-123.
9. Б.М. Левитан, Вычисление регуляризованного следа для оператора Штурма-Лиувилля // УМН. 1964. Т.19. №1. С.161-165.
10. В.Б. Лидский, В.А. Садовничий, Регуляризованные суммы корней одного класса целых функций // Докл. АН СССР. 1967. Т. 176. №2. С. 259-262.
11. В.А. Марченко, Операторы Штурма-Лиувилля и их приложения, Киев: Наукова думка, 1977.
12. В.А. Винокуров, В.А. Садовничий, Собственное значение и след оператора Штурма-Лиувилля как дифференцируемые функции суммируемого потенциала // Докл. РАН. 1999. Т. 365. №3. С.295-297.
13. А.М. Савчук, Регуляризованный след первого порядка оператора Штурма-Лиувилля с --- потенциалом // УМН. 2000. Т.55. №6(336). С.155-156.
14. А.М. Савчук, А.А. Шкаликов, Операторы Штурма-Лиувилля с сингулярными потенциалами // Матем. заметки. 1999. Т.66. №6, С. 897-912
15. S. Albeverio, F. Gesztesy, R. Hoegh-Krohn, H. Holden, Solvabel models in quantum mechanics, New Yourk: Springer, 1988 (Second edition: AMS, 2005)
16. Б.К. Кокебаев, М. Отелбаев, А.Н. Шыныбеков, К вопросам расширения и сужения операторов // Доклады АН СССР. 1983. Т. 271, №6. С. 1307-1311.
17. B.E. Kanguzhin and D.B. Nurakhmetov, Boundary Value Problems for 2nd Order Non-homogeneous Differential Equations with Variable Coefficients// Journal of Xinjiang University (Natural Science Edition). 2011. Vol. 28, 28 (Sum.121), №1, Р. 47-56.
18. Кангужин Б.Е., Анияров А.А. Корректные задачи для оператора Лапласа в проколотой области // Матем. заметки, 2011, Т.89, №6, С. 856-867
19. Кангужин Б.Е., Нурахметов Д.Б., Токмагамбетов Н.Е. Оператор Лапласа с ![]() -подобными потенциалами // Изв. вузов. Матем., 2014, №2, С. 9-16.
-подобными потенциалами // Изв. вузов. Матем., 2014, №2, С. 9-16.
0 комментариев