ЛИСТ ЗАМЕЧАНИЙ
ОГЛАВЛЕНИЕ
1 ЗАДАЧА.. 4
1.1ИСХОДНЫЕ ДАННЫЕ. 4
2 АНАЛИЗ РАБОТЫ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ. 5
2.1 ОБЛАСТЬ ПРИМЕНЕНИЯ. 5
2.2 АНАЛИЗ ИСХОДНЫХ ДАННЫХ. 5
2.3 РАЗРАБОТКА ФУНКЦИОНАЛЬНОЙ СХЕМЫ САР. 6
2.4 АНАЛИЗ ДЕЙСТВУЮЩИХ НА СИСТЕМУ ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ, АНАЛИЗ ИХ ВЛИЯНИЯ НА СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ САР. 6
2.5 ПРИНЦИП РАБОТЫ СИСТЕМЫ.. 6
2.6 КЛАССИФИКАЦИЯ РАССМАТРИВАЕМОЙ САР. 8
2.7 ПОЛУЧЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ЗВЕНЬЕВ САР. 8
2.8 СТРУКТУРНАЯ СХЕМА САР. 11
2.9 Передаточные функции разомкнутой и замкнутой систем.. 11
2.10 УРАВНЕНИЯ ДИНАМИКИ ЗАМКНУТОЙ САР. 13
2.11 Анализ структурной устойчивости САР: 13
2.12 РАСЧЕТ КОЭФФИЦИЕНТА УСИЛЕНИЯ ЭЛЕКТРОННОГО УСИЛИТЕЛЯ. 14
2.13 Анализ динамической устойчивости САР по критериям Рауса, Гурвица, Михайлова, Найквиста. Вывод по результатам анализа. 15
2.13.1 Критерий Гурвица. 15
2.13.2 Критерий Рауса. 16
2.13.3 Критерий Михайлова. 17
2.13.4 Критерий Найквиста. 18
Вывод по результатам анализа. 19
2.14 D – РАЗБИЕНИЕ В ПЛОСКОСТИ ОДНОГО ВАРЬИРУЕМОГО ПАРАМЕТРА. ПОСТРОЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ НЕСКОРРЕКТИРОВАННОЙ САР. 20
2.15 ПОСТРОЕНИЕ ГРАФИКА ПЕРЕХОДНОГО ПРОЦЕССА ЗАМКНУТОЙ СИСТЕМЫ ПО ЗАДАЮЩЕМУ ВОЗДЕЙСТВИЮ... 21
ЗАКЛЮЧЕНИЕ. 22
СПИСОК ЛИТЕРАТУРЫ.. 23
1 ЗАДАЧА
В данной курсовой работе необходимо проанализировать работу и устойчивость системы автоматического регулирования частоты вращения двигателя постоянного тока с электромашинным усилителем мощности.
1.1 ИСХОДНЫЕ ДАННЫЕ
Исходные данные:
1.Коэффициент передачи ДПТ по регулирующему воздействию [об/(мин*В)], k3 - 10,0;
2. Электромеханическая постоянная времени ДПТ [c], Tм - 0,28;
3. Коэффициент передачи ЭМУ, k2 - 10,0;
4. Постоянная времени короткозамкнутой цепи ЭМУ [c], Tq - 0,07;
5. Постоянная времени цепи управления ЭМУ [c], Ty - 0,002;
6. Коэффициент передачи тахогенератора [(B*c)/об], k4 - 0,6;
7. Постоянная времени якоря ДПТ [c], Тя - 0,035;
8. Коэффициент передачи ДПТ по возмущающему воздействию [об/(мин*кгм)], k5 - 2,7.
Статическая ошибка регулирования [%], ε – 0,6.
Численные значения показателей качества:
1. Время регулирования [c] – 0,5;
2. Величина максимального перерегулирования [%] – 25;
3. Закон изменения задающего воздействия – 1(t).
2 АНАЛИЗ РАБОТЫ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
2.1 ОБЛАСТЬ ПРИМЕНЕНИЯ
Подобная система регулирования находит свое применение в таких устройствах и системах как:
судовом электроприводе большой мощности;
прокатных станах (синхронная работа клетей);
высокооборотном приводе вакуумных турбомолекулярных насосов (до 100 000 об/мин.);
конвейерных системах;
мешалках, насосах, вентиляторах, компрессорах;
стиральных машинах;
а также в других устройствах и системах, где требуется стабилизация частоты вращения вала.
2.2 АНАЛИЗ ИСХОДНЫХ ДАННЫХ
Наличие показателя статической ошибки регулирования свидетельствует о том, что это статическая система.
2.3 РАЗРАБОТКА ФУНКЦИОНАЛЬНОЙ СХЕМЫ САР
|
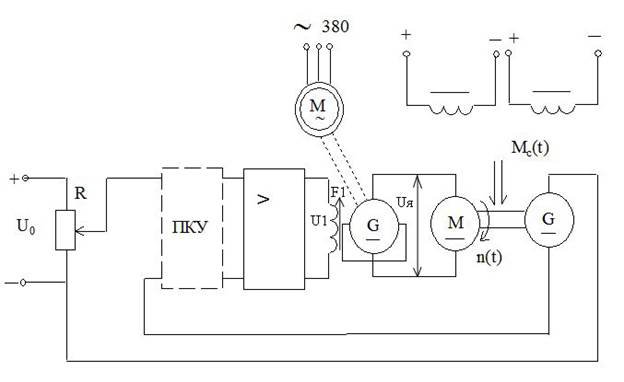
Рисунок 2.1 – Функциональная схема системы автоматического регулирования частоты вращения двигателя постоянного тока с электромашинным усилителем мощности
2.4 АНАЛИЗ ДЕЙСТВУЮЩИХ НА СИСТЕМУ ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ, АНАЛИЗ ИХ ВЛИЯНИЯ НА СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ САР
К основному, оказывающему самое сильное влияние на систему возмущающему воздействию относится момент сопротивления вала двигателя. Также, небольшое воздействие оказывают переменное напряжения двигателя переменного тока.
2.5 ПРИНЦИП РАБОТЫ СИСТЕМЫ
При помощи потенциометра R регулируем напряжение U0, поступающее на усилитель. U0 определяется формулой:
U0=UR-Uтг, (1)
где UR– напряжение после преобразования на потенциометре R, В;
Uтг – напряжение тахогенератора, В;
При повышении U0 увеличится и напряжение U1. Повышение напряжения
вызовет увеличение тока i1 протекающего в катушке. Далее из формулы:
F1=w1·i1; (2)
где F1 – намагничивающая сила;
w1 – количество витков в катушке;
следует что, при увеличении тока i1 увеличится и F1. При увеличении F1 увеличится напряженность магнитного поля создаваемого катушкой.
![]() ; (3)
; (3)
где l – длина обмотки катушки, м;
При увеличении напряженности магнитного поля увеличится и магнитная индукция B1. Увеличение магнитной индукции вызовет увеличении магнитного потока Ф1, протекающего через катушку:
Ф1=B1·S; (4)
Увеличение магнитного потока, протекающего через электромашинный усилитель вызовет в нем увеличение напряженности электрического поля:
Eэму=CenФ1; (5)
где Ce – электрическая постоянная электромашинного усилителя;
n – частота вращения вала, с-1;
Увеличение Eэму приведет к увеличению напряжения на якоре. Это следует из формулы:
Uя=Eэму+iя·Rя; (6)
где iя – ток якоря, А;
Rя – сопротивление якоря, Ом;
В свою очередь это вызовет повышения напряжения Uдпт на двигателе постоянного тока. Что приведет к повышению частоты вращения вала n.
Если момент сопротивления Mc повышается, то частота вращения вала начинает понижаться и системе необходимо восстановить скорость вращения вала до прежнего уровня. Принцип действия можно изобразить при помощи следующей логической цепочки:
↑Mc → ↓n → ↓Uтг → ↑U0=UR-↓Uтг→↑U1 → ↑i1 → ↑F1 → ↑H1 → ↑B1 → ↑Ф1 → ↑Eэму → ↑Uя → ↑Uдпт → ↑n.
Таким образом, САР следит за частотой вращения вала и стабилизирует ее при необходимости.
2.6 КЛАССИФИКАЦИЯ РАССМАТРИВАЕМОЙ САР
Данная САР является стабилизирующей, так как стабилизирует частоту вращения вала двигателя; непрерывной, так как в системе нет дискретных звеньев; линейной, так как описывается линейными дифференциальными уравнениями; замкнутой, так как содержит замкнутый контур; стационарной, так как ее свойства не изменяются с течением времени.
2.7 ПОЛУЧЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ЗВЕНЬЕВ САР
Считая электронный усилитель безынерционным, его передаточную функцию W1(p) можно записать как:
W1(p)=k1; (7)
где k1 – коэффициент усиления по напряжению электронного усилителя.
В режиме, близком к холостому ходу, тахогенератор можно считать усилительным звеном, если входной величиной является угловая скорость:
W4(p)=k4, (8)
где k4 – коэффициент передачи тахогенератора.
При постоянном внешнем возбуждении скорость вращения вала двигателя зависит от падений напряжения в цепи якоря и внешних механических усилия на валу, поэтому для описания его работы необходимо иметь два исходных дифференцированных уравнения. Первое уравнение может быть получено на основании записи второго закона Кирхгофа для цепи якоря:
![]() , (9)
, (9)
где Lя – индуктивность обмотки якоря;
iя – ток в обмотке якоря;
Rя – активное сопротивление обмотки якоря;
Ф – магнитный поток обмотки возбуждения;
U– напряжение(входная величина);
Се – коэффициент пропорциональности.
Второе уравнение запишем на основании закона равновесия моментов на валу якоря, оно имеет вид:
![]() , (10)
, (10)
где J – приведенный момент инерции вала двигателя;
Ф – магнитный поток обмотки возбуждения двигателя;
Cм – коэффициент пропорциональности.
Для приращений переменных параметров с учетом малых отклонений при условии постоянства магнитного потока обмотки возбуждения и отсутствии возмущающего воздействия (M = 0) можно записать следующую систему уравнений:
![]() , (11)
, (11)
![]() , (12)
, (12)
Из уравнения (12) получим:
![]() , (13)
, (13)
Подставим (13) в (11) и перейдем к операторной форме записи. В результате получим:
![]() , (14)
, (14)
Разделим обе части уравнения на Cе и перегруппируем слагаемые:
![]() , (15)
, (15)
Вводим новые обозначения и переходим к стандартной форме записи дифференциального уравнения:
![]() , (16)
, (16)
где - ![]() – постоянная времени якоря;
– постоянная времени якоря;
k3 – коэффициент передачи двигателя по задающему воздействию (k3=1/Ce).
![]() – электромеханическая постоянная времени двигателя;
– электромеханическая постоянная времени двигателя;
Тогда передаточная функция двигателя по задающему воздействию будет иметь вид:
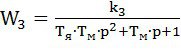 . (17)
. (17)
Передаточную функцию двигателя по возмущающему воздействию можно представить таким образом:
W5=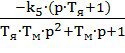 (18)
(18)
где k5=![]() - коэффициент передачи ДПТ по возмущающему воздействию.
- коэффициент передачи ДПТ по возмущающему воздействию.
Передаточная функция ЭМУ:
W2=![]() ; (19)
; (19)
где – Ed и Uу соответственно операторные изображения э.д.с. якоря по продольной оси и напряжения на управляющей обмотке;
Операторные уравнения для цепи обмотки управления и поперечной цепи якоря ЭМУ:
Lу9p9Iу + Rу9Iу = Uу; (20)
Lq9p9Iq + Rq9Iq = Eq; (21)
где Iу и Iq - токи соответственно в цепи управления и поперечной цепи якоря;
Электродвижущая сила, действующая по поперечной оси якоря, в пределах линейного участка кривой намагничивания машины пропорциональна магнитодвижущей силе Fу, развиваемой обмоткой управления:
Eq = v19Fy = v19wy9 Iу; (22)
Электродвижущая сила якоря по продольной оси пропорциональна поперечной магнитодвижущей силе якоря Fq, создаваемой током Iq:
Ed = v29Fq = v29wa9Iq; (23)
где в уравнениях (22) и (23) wa – число активных витков якоря ЭМУ;
v1 и v2 – коэффициенты пропорциональности;
Подставив значения Iy и Iq из формул (22) и (23) соответственно в (20) и (21), получим передаточные функции двух каскадов усиления ЭМУ:
![]() =
= 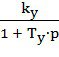 ; (24)
; (24)
![]() =
= 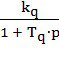 ; (25)
; (25)
где ky =![]() и kq =
и kq =![]() – передаточные функции каскадов усиления;
– передаточные функции каскадов усиления;
Ту = ![]() - постоянная времени цепи управления ЭМУ;
- постоянная времени цепи управления ЭМУ;
Тq = ![]() – постоянная времени поперечной цепи ЭМУ;
– постоянная времени поперечной цепи ЭМУ;
Таким образом, ЭМУ с поперечным полем может быть представлен в виде двух последовательных апериодических звеньев направленного действия.
Следовательно передаточная функция электромашинного усилителя:
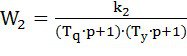 , (26)
, (26)
где – k2 = ![]() – коэффициент передачи ЭМУ.
– коэффициент передачи ЭМУ.
2.8 СТРУКТУРНАЯ СХЕМА САР
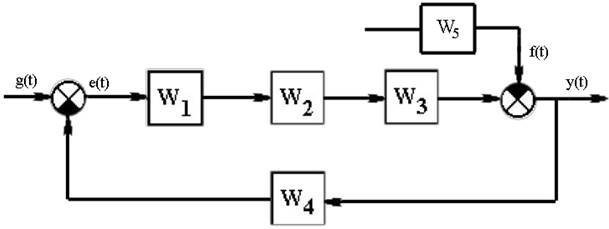
Рисунок 2.2 – Структурная схема системы автоматического регулирования частоты вращения двигателя постоянного тока с электромашинным усилителем мощности
2.9 Передаточные функции разомкнутой и замкнутой систем
С учетом исходных данных получаем:
W1=k1;
W2=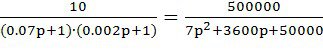 ;
;
W3=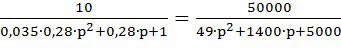 ;
;
W4=0,6;
W5= ![]() ;
;
Передаточная функция обратной связи Wос=W4=0,6. Так как звенья соединены последовательно, то передаточная функция W(p) разомкнутой системы с учетом неединичной обратной связи определяется как:
W(p)=Wпк=W19W29W39W4; (27)
W(p)= ;
;
Передаточная функция возмущающего воздействия Wв=W5. Тогда передаточная функция разомкнутой системы по возмущающему воздействию Wf(p) равна:
Wf(p)= -W5= 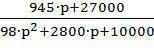 ; (28)
; (28)
Обратную связь в последующих расчетах можно принять как единичную, так как она уже была учтена в W(p). Передаточная функция замкнутой системы Ф(р) с учетом единичной обратной связи будет определяться как:
Ф(p)=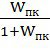 ; (29)
; (29)
Ф(р)=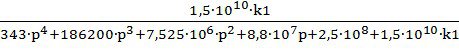 ;
;
Передаточная функция замкнутой системы по возмущающему воздействию
Фf(р) определяется следующей формулой:
Фf(р)=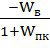 ; (30)
; (30)
Фf(р)= )÷
)÷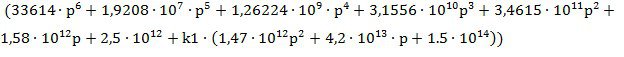 ;
;
Передаточная функция замкнутой системы по ошибке Ф(р):
Ф(р)=1-Ф(р); (31)
Ф(р)=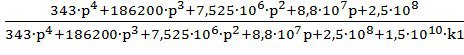 ;
;
2.10 УРАВНЕНИЯ ДИНАМИКИ ЗАМКНУТОЙ САР
Дифференциальное уравнение замкнутой системы относительно сигнала ошибки можно записать как:
D(p)9(t) = Q’(p)9g(t) + N’(p)9f(t), (32)
где D(p) = ![]() ;
;
Q’(p) = ![]() ;
;
N’(p) = -  ;
;
Тогда:
![]() 9 (t)
9 (t)
= ![]() 9g(t) -
9g(t) -
- 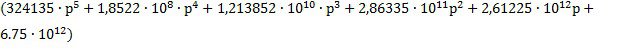 9f(t).
9f(t).
Дифференциальное уравнение замкнутой системы относительно выходной величины записывается следующим образом:
D(p)9y(t) = R’(p)9g(t) - N’(p)9f(t), (33)
где – R’(p) = ![]() ;
;
Тогда:
![]() 9 y(t)
9 y(t)
= ![]() 9g(t) +
9g(t) +
+ 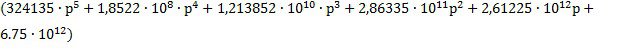 9f(t).
9f(t).
2.11 Анализ структурной устойчивости САР:
Для анализа структурной устойчивости САР необходимо проанализировать характеристический полином передаточной функции разомкнутой системы. Упростив значение передаточной функции замкнутой системы получим:
W(р)=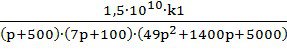 ;
;
Из данного выражения можно судить что:
q=0;
r=0;
t=0;
m=0;
n=4;
где – q – число сомножителей вида p в знаменателе передаточной функции;
r – число сомножителей вида (T2p2 + 1) в знаменателе передаточной функции;
t – число сомножителей вида (T9p – 1) в знаменателе передаточной функции;
m – степень полинома числителя;
n – степень полинома знаменателя;
Тогда :
N = m + n = 4; (34)
μ = q + t + 2r = 0; (35)
ρ = 0,
где ρ – целая часть дроби μ/2;
В данном случае, чтобы система была структурно устойчивой, необходимо чтобы выполнялось неравенство:
N > 49ρ;
4 > 0;
Неравенство выполняется, следовательно данная система структурно устойчива.
2.12 РАСЧЕТ КОЭФФИЦИЕНТА УСИЛЕНИЯ ЭЛЕКТРОННОГО УСИЛИТЕЛЯ
Статическая ошибка регулирования ε САР по задающему воздействию y(t)=1(t) определяется выражением:
ε = ![]() ; (36)
; (36)
где – k =  k1 = 609k1 – коэффициент усиления передаточной функции разомкнутой системы;
k1 = 609k1 – коэффициент усиления передаточной функции разомкнутой системы;
g0 = 1 – значение задающего воздействия в установившемся режиме;
Преобразовывая выражение (36) получим:
k = 1/ε -1; (37)
k = 1/0,006 – 1 = 165,67;
Тогда коэффициент электронного усилителя k1 будет равен:
k1 = k/![]() =
= ![]() = 2,762.
= 2,762.
С учетом k1 получим точные выражения W(p) и Ф(p):
W(p)=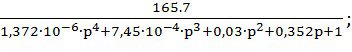
Ф(р)=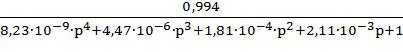 ;
;
2.13 Анализ динамической устойчивости САР по критериям Рауса, Гурвица, Михайлова, Найквиста. Вывод по результатам анализа
2.13.1 Критерий Гурвица
В соответствии с данным критерием, САР является динамически устойчивой, если все определители матрицы Гурвица положительны. Если же есть отрицательный определитель, то неустойчива.
Характеристический полином передаточной функции замкнутой системы:
D(p) =![]() ;
;
Коэффициенты характеристического полинома:
a0 = ![]() ;
;
a1 = ![]()
a2 = ![]()
a3 = ![]() ;
;
a4 = ![]() ;
;
Матрица Гурвица имеет вид:
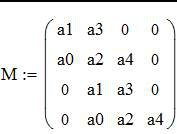 ; (38)
; (38)
Тогда определители:
![]() ;
;
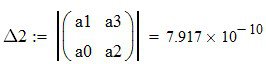 ;
;
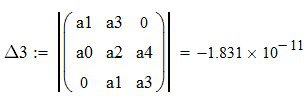 ;
;
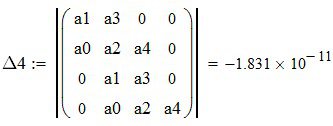 ;
;
Есть два отрицательных определителя, значит система динамически неустойчива.
2.13.2 Критерий Рауса
В соответствии с данным критерием САР является динамически устойчивой,
если все значения первого столбца таблицы Рауса положительны. Если же есть отрицательные значения, то система динамически не устойчива.
Таблица 1 – Общий вид таблицы Рауса
| Значение r | № строки | № столбца | ||
| 1 | 2 | 3 | ||
| - | 1 | a0 | a2 | a4 |
| - | 2 | a1 | a3 | 0 |
| r0 | 3 | C13 | C23 | C33 |
| r1 | 4 | C14 | C24 | C34 |
| r2 | 5 | C15 | C25 | C35 |
где – r0 = a0/a1 = 1,841910-3;
C13 = a2 - r09a3 = 1,771910 -4;
C23 = a4 - r090 = 1;
С33=0;
r1 = a1/ C13 = 0,025;
C14 = a3 – r19 C23 = -0,023;
С24=0;
r2 = C13/ C14 = - 7,658910 -4;
С15 = С23 – r29C24 = 1;
Тогда:
Таблица 2 – Полученная таблица Рауса
| Значение r | № строки | № столбца | ||
| 1 | 2 | 3 | ||
| - | 1 |
|
|
|
| - | 2 |
|
| 0 |
| 1,841910-3 | 3 | 1,771910 -4 | 1 | 0 |
| 4 | -0,023 | 0 | 0 | |
| 5 | 1 | 0 | 0 | |
Как видно из полученной таблицы Рауса, в четвертой строке первого столбца есть отрицательное значение. Значит система динамически неустойчива.
2.13.3 Критерий Михайлова
Для проверки динамической устойчивости по данному критерию, построим годограф Михайлова. Для этого заменим p в характеристическом полиноме D(p)
на ω9i, где:
ω – угловая частота;
i – мнимая единица;
Получим:
D(ω9i) = ![]() ;
;
Vd(ω) – мнимая часть полинома D(ω9i), Ud(ω) – действительная часть. Построим годограф Михайлова Vd(ω)=ƒ(Ud(ω)) при ω ∈ [0; +∞):
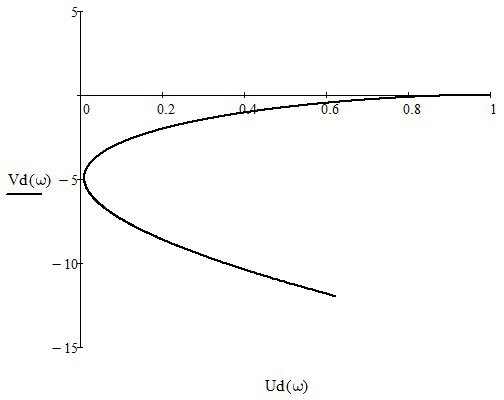
Рисунок 2.3 – Годограф Михайлова Vd(ω)=ƒ(Ud(ω)) при ω ∈ [0; 120]
Из графика видно, что годограф неправильный, значит система динамически неустойчива.
2.13.4 Критерий Найквиста
Характеристический полином передаточной функции разомкнутой системы Q(p) представляет собой:
Q(p)=![]()
Приравняем к нулю и получим корни уравнения:
p1 = - 4,18;
p2 = - 24,39;
p3 = - 14,29;
p4 = - - 500,0;
Видно, что все корни принадлежат левой части комплексной плоскости. Значит разомкнутая система устойчива. Построим АФЧХ разомкнутой системы. Для этого заменим в выражении передаточной функции разомкнутой системы p на ω9i, и построим график, где на оси мнимых чисел будут значения мнимой части полученного выражения, а на оси вещественных чисел – вещественной:
W(ω9i) = ![]() ;
;
Выделим вещественную Re(W(ω9i)) и мнимую Im(W(ω9i)) части, и построим график Im(W(ω9i)) = ƒ(Re(W(ω9i))) при ω ∈ [0; +∞):
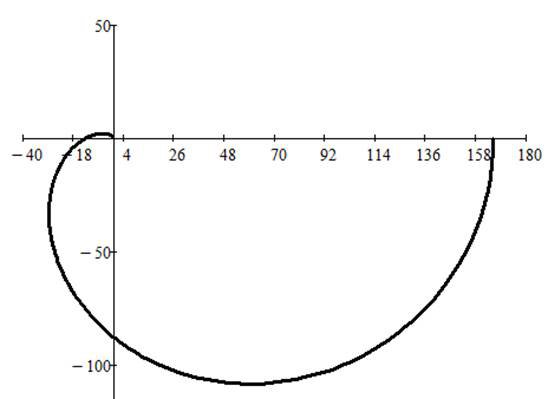
Рисунок 2.4 – АФЧХ разомкнутой системы
Для того, чтобы замкнутая система являлась динамически устойчивой, необходимо чтобы график АФЧХ не охватывал точку с координатами (-1; j0). Как видно из графика АФЧХ, она охватывает эту точку, значит замкнутая система динамически неустойчива.
Вывод по результатам анализа
В ходе анализа по четырем критериям динамической устойчивости замкнутой системы все критерии показали, что замкнутая система динамически неустойчива.
2.14 D – РАЗБИЕНИЕ В ПЛОСКОСТИ ОДНОГО ВАРЬИРУЕМОГО ПАРАМЕТРА. ПОСТРОЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ НЕСКОРРЕКТИРОВАННОЙ САР
Передаточная функция разомкнутой системы представляет собой:
W(p)=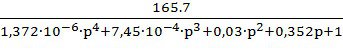 ;
;
Тогда характеристический полином замкнутой системы с учетом единичной обратной связи:
D(p) = ![]() ;
;
В соответствии с условием устойчивости D(p) = 0, получим выражение для
коэффициента усиления разомкнутой системы k(p):
k(p) = ![]() ;
;
Заменим p = ω9i:
k(ω9i) = ![]() ;
;
Тогда Uk(ω) – действительная часть k(ω9i), Vk(ω) – мнимая.
|
|
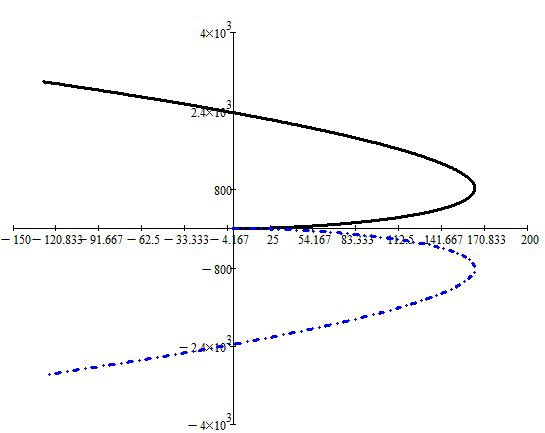
Рисунок 2.5 – Построение областей устойчивости Vk(ω) = ƒ(Uk(ω)) при ω ∈ [-160; 160]
|
|
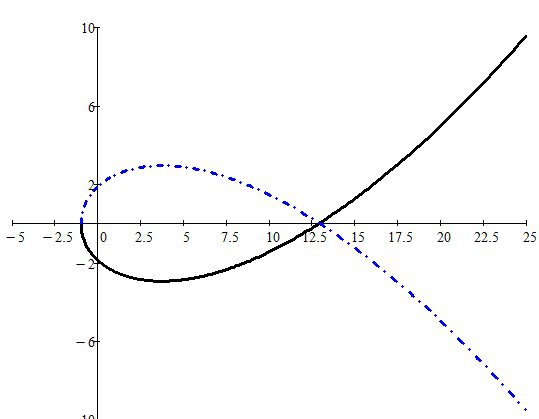
Рисунок 2.6 – Построение областей устойчивости Vk(ω) = ƒ(Uk(ω)) при ω ∈ [-30; 30]
Таким образом, система будет устойчива при значении коэффициента усиления разомкнутой системы k ∈ [0; 13].
2.15 ПОСТРОЕНИЕ ГРАФИКА ПЕРЕХОДНОГО ПРОЦЕССА ЗАМКНУТОЙ СИСТЕМЫ ПО ЗАДАЮЩЕМУ ВОЗДЕЙСТВИЮ
Для исследования переходного процесса замкнутой САР необходимо коэффициент передаточной функции разомкнутой системы заменить на число, входящее в область устойчивости замкнутой системы. Возьмем коэффициент k=6. Получим передаточную функцию разомкнутой системы:
W(p)=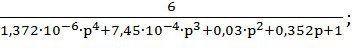
Тогда передаточная функция замкнутой системы Ф(р) примет вид:
Ф(p)=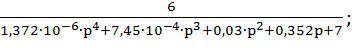
Построим график переходного процесса замкнутой системы:
|
|
|
|
|
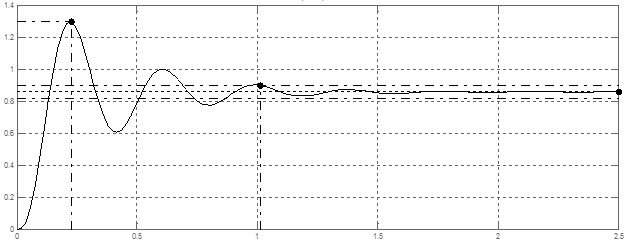
Рисунок 2.7 – График переходного процесса замкнутой системы по задающему воздействию
где - gmax= 1,3 – максимальное амплитудное значение входного сигнала;
g(∞) = 0,853 – установившееся значение входного сигнала;
tр = 1,02 – время регулирования(время протекания переходного процесса), с;
6 = 5%;
Из полученных параметров можно найти полученные перерегулирование σ% и статическую ошибку ε:
σ% = 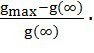 100%; (39)
100%; (39)
σ% = 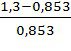 9 100% = 52,4, %;
9 100% = 52,4, %;
ε = 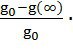 100%; (40)
100%; (40)
ε = ![]() 100% = 14,7, %;
100% = 14,7, %;
ЗАКЛЮЧЕНИЕ
Как можно наблюдать из полученного графика переходного процесса, длительность переходного процесса и статическая ошибка сильно превышают установленные в задании значения. В таком виде система непригодна для исполь- зования. Для достижения требуемого качества и параметров системы автоматичес- кого регулирования необходим синтез последовательного корректирующего устройства.
СПИСОК ЛИТЕРАТУРЫ
1. Башарин А.В., Голубев Ф.Н., Кепперман В.Г. Примеры расчетов автоматизированного электропривода. - Л.: Энергия, 1972. 440с.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – С-П.: Профессия, 2004.747 с.
3. Васильев Д.В. (и др.) Примеры и задачи по расчету судовых автоматизированных систем. - Л.: Судостроение, 1973. 296с.
4. Воронов А.А. (и др.) Основы теории автоматического регулирования и управления. М.: Высшая школа, 1977. 519с.
5. Горбацевич Е.Д.. Левинзон Ф.Ф. Аналоговое моделирование систем управления. М.: Наука, 1984.304с.
6. Заборовский В.С., Козлов В.Н., Куприянов В.Е. Теория автоматического управления и системы с ЭВМ. Учеб. пособие. Л.: ЛГУ, 1990.96с.
7. Зайцев Г.Ф. (и др.) Основы автоматического регулирования и управления. - Киев.: Технiка, 1975. 495с.
8. Иващенко Н.Н. Автоматическое регулирование. М. Машиностроение.
1978.735с.
9. Куропаткин И.В. Теория автоматического управления. - М,: Высшая школа,1973.527с.
10. Макаров И.М., Менский Б.М. Линейные автоматические системы. М.: Машиностроение, 1982.540с.
11. Нечаев Н.Н. (и др.) Методические указания по оформлению пояснительных записок и графической части домашних заданий, курсовых и дипломных проектов и работ. Л.: ЛКИ, 1984.
12. Попов Е.П. Теория линейных систем автоматического регулирования и управления.: Учеб. пособие для втузов. - М.: Наука, 1989. 340с.
13. Расчет автоматических систем, /под ред. Л.В. Фатеева/. Учеб. пособие для вузов. - Л.: Высшая школа, 1973. 336с.
14. Справочник по теории автоматического управления. /Под ред. А.А. Красовского/. - М.: Наука, 1987. 712с.
15. Справочное пособие по теории систем автоматического регулирования и управления. /Под ред. Е.А. Санковского/. Мн.: Вышэйш. школа, 1973. 584с.
16. Суевалов Л.Ф. Справочник по расчетам судовых автоматическихсистем.- Л.: Судостроение, 1977. 375с.
Похожие материалы
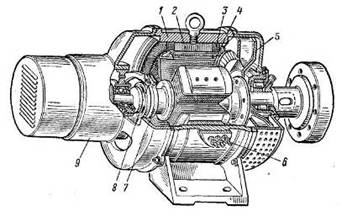
... особенностью машины постоянного тока является наличие коллектора и скользящего контакта между обмоткой якоря и внешней электрической цепью. 2.2 Устройство машины постоянного тока Машина постоянного тока (рис. 2.3) по конструктивному исполнению подобна обращенной синхронной машине, у которой обмотка якоря расположена на роторе, а обмотка возбуждения – на статоре. Основное отличие заключается ...
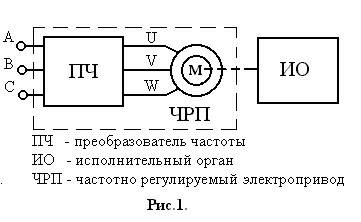
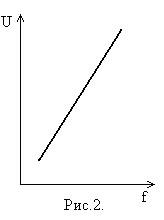
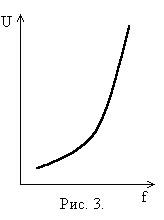
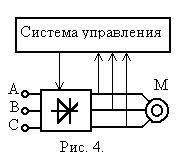
... 3 - 10 кВ и выше. Однако их цена на один кВт выходной мощности самая большая в классе высоковольтных преобразователей. До недавнего прошлого преобразователи частоты на GTO составляли основную долю и в низковольтном частотно регулируемом приводе. Но с появлением IGBT транзисторов произошел «естественный отбор» и сегодня преобразователи на их базе общепризнанные лидеры в области низковольтного ...
... переходного процесса для системы с дискретным корректирующим звеном. 2.6.8. Определение рекуррентного уравнения дискретного корректирующего звена. 2.6.9. Разработка принципиальной схемы цифровой следящей системы. 2.7. Расчетно-пояснительная записка должна содержать следующие разделы. 2.7.1. Введение (цель выполнения работы, описание следящей системы, принцип ее ...
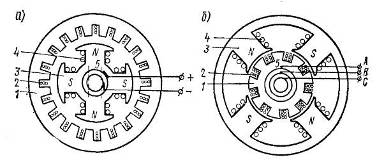
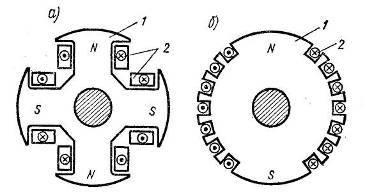
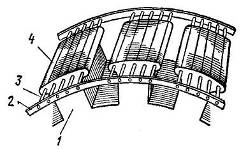
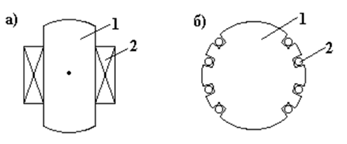
... , представляющий собой ферромагнитный цилиндр 1. На поверхности ротора в осевом направлении фрезеруют пазы, в которые укладывают обмотку возбуждения 2. Рис. 12.10 Рассмотрим принцип работы синхронного двигателя на модели (рис. 12.11). Рис. 12.11 Вращающееся магнитное поле статора представим в виде магнита 1. Намагниченный ротор изобразим в виде магнита 2. Повернем магнит 1 ...

0 комментариев