Қазақстан Республикасы Білім және ғылым министрлігі
Абай атындағы Қазақ ұлттық педагогикалық
университеті
Нұржұмаева Тоғжан Оразгазықызы
«Сызықты дифференциалдық теңдеулер жүйесін интегралдаудың матрицалық-векторлық тәсілі туралы»
Дипломдық жұмыс
«5В010900»-«Математика»
Алматы 2015
Қазақстан Республикасы Білім және ғылым министрлігі
Абай атындағы Қазақ ұлттық педагогикалық
университеті
«Қорғауға жіберілді»
Фундаментальды және Қолданбалы математика
Кафедрасының меңгерушісі
дф-м н.д. профессор_____________________ Алдашев С.А
Дипломдық жұмыс
Тақырыбы: «Сызықты дифференциалдық теңдеулер жүйесін интегралдаудың матрицалық-векторлық тәсілі туралы»
«5В010900»-«Математика»
Орындаған: Нұржұмаева Т
Ғылыми жетекші:
Алматы 2015
МАЗМҰНЫ:
КІРІСПЕ….............................................................................................................
I.СЫЗЫҚТЫ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІ
1.1 Біртекті сызықты теңдеулер жүйесі
1.1.1 Біртекті жүйесінің шешімдерінің негізгі қасиеттері
1.1.2 Остроградский – Лиувилль– Якоби формуласы
1.1.3 Жалпы шешімін құру
1.2 Біртекті емес сызықты теңдеулер жүйесі
1.2.1 Біртекті емес жүйенің ортақ шешімінің құрылымы
1.2.2 Тұрақты ерік түрлендіру әдісі
II. БІРТЕКТІ СЫЗЫҚТЫ ЖҮЙЕЛЕРДІ МАТРИЦАЛЫҚ ӘДІСПЕН ИНТЕГРАЛДАУ
2.1 Біртекті сызықтық жүйені матрицалық түрде интегралдау және жазылуы
2.1.1 Матрицалық теңдеудің біртекті сызықты жүйеге қатысты екі ортақ
қасиеті
2.1.2 Интегралды матрицаның негізгі қасиеттері
2.1.3 Лаппо – Данилевский жағдайы
2.2 Тұрақты коэфициенттері бар біртекті сызықтық жүйені интегралдау
2.2.1 Дифференциалдық теңдеулердің тұрақты коэфициенттерімен
біртекті сызықтық жүйенің шешімдерінің фундаментальді жүйесінің
құрылымы
2.2.2 Біртекті сызықтық жүйені тұрақты коэфициенттерімен канондық түрге
келтіру
2.3 Сызықты жүйелерді матрицалық-векторлық әдіспен интегралдау
2.3.1 Сызықты жүйенің матрицалық-векторлық түрде жазылуы мен шешімі.
Коши есебі.
2.3.2 Біртекті матрицалық-векторлық теңдеуді шешудің негізгі қасиеттері
2.3.3 Біртекті емес сызықты жүйе үшін Коши формуласы
ҚОРЫТЫНДЫ........................................................................................................
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР.........................................................................
ҚОСЫМШАЛАР....................................................................................................
КІРІСПЕ
Дифференциалдық теңдеулер курсына арналған бұл «Сызықты дифференциалдық теңдеулер жүйесін интегралдаудың матрицалық-векторлық тәсілі туралы» атты ғылыми жұмысты жоғары оқу орнындарында оқитын математика, физика және информатика мамандығының қазақ жастарының студенттері пайдалануға болады. Бұл жұмыстың әр тарауында теорияны игеру мақсатында көптеген мысалдар мен есептер шығарылған.
Дифференциалдық теңдеулер курсы студенттердің белгілі бір математикалық мәдениетін немесе олардың ғылыми, әсіресе математиканы оқытудың практикалық және қолданбалы бағыттарының мәнін түсіну, сол сияқты математикалық модельдеудің әдістерін меңгеру мен пәнаралық байланыстарды жүзеге асыру іскерлігі сияқты көзқарастырын қалыптастыру тұрғысынан болсын болашақ мұғалімдердің іргелі математикалық дайындықтарына атқарар ролі аса зор.
Дифференциалдық теңдеулер пәні ғылыми зерттеу және қолданбалы матемикада көптен пайданылып, бұл пен математикалық анализ, сызықты алгебра және аналитикалық геометрия негізінде құрылады.
“Дифференциалдық теңдеулер” пәнін оқытудың мақсаты– студенттердың жай дифференциалдық теңдеулер теориясының негізі бойынша терең білімдерін қалыптастыру, жаратылыстанудың әр-түрлі облыстарындағы кездесетін дифференциалдық теңдеулер мен жүйелерді шешуге және зерттеуге алған білімдерін қолдануға уйрету.
“Дифференциалдық теңдеулер” пәні жай дифференциалдық теңдеулердің және бірінші ретті дербес туындылы теңдеулердің шешімдерін табуға, оларды зерттеуге арналған.
Жоғары математиканы кей уақытта айнымалы шамалар математикасы деп те айтады.
Айнымалы шамалар математикасындағы келесі шешуші адым XVII ғасырдың екінші жартысында (дал айтқанда, май 1684 ж.) дифференциалдық және интегралдық есептеулердің «дүниеге келуі» болды. Мұны математакалық анализдің немесе шексіз аздар анализінің тууы деп есептейді.
Дифференциалдық және интегралдық есептеулердің тууына себепші болған физика мен геометрияның келесі есептері: жазықтыкта немесе кеңістікте қозғалушы материалды нүктенің кез келген уақыттың ішіндегі жылдамдығын табу, жазықтықта жатқан қисық сызықтың берілген нүктесінде оған жанама жүргізу, фигуралардың аудандарын және денелердің көлемдерін табу керек.
Жаратылыстану ғылымдары мәселелерін қандай жаңа әдіспен сипаттауға болады деген сұраққа XVII—XVIII ғасырлардағы математиктер: — егер бұл ғылымдардың кез келген мәселелері дұрыс математикалық сипаттауға келтірілетін болса, онда олардың шешуін аналитикалық геометрия, дифференцияалдық және интегралдық есептеудің көмегімен табуға болады, — деп жауап берді. Бірақ ғалымдардың бұл пікірлері.тура келмеді, өйткені жаратылыстану ғылымдары мен техниканың жаңағы салалардың әлі келмейтін күрделі мәлелелері бірте-бірте кездесе берді. Осындай күрделі мәселелерді шешудің арқасында математикалық анализдің мынадай салалары: дифференциалдық теңдеулер, вариациялық есептеу, интегралдық теңдеулер, комплекс айнымалылар функцияларының теориясы, функционалдық анализ, ықтималдық теориясы атты тағы да басқа салалары пайда болды.
Дифференциалдық теңдеулер теориясы — математикалық анализдің ең маңызды және жаратылыстану ғылымдары (физика, астрономия, механика т. б.) мен техниканың мәселелерін шешуде ерекше орын алатын саласы болып табылады. Дифференциалдық теңдеу бір шаманың екінші бір шамаларға тәуелділік заңын береді. Бұл теңдеулердегі белгісіздер бір айнымалы немесе екі, үш және онан да көп айнымалы шамалардың функциялары болып табылады.
Механикада қозғалушы дененің қозғалыс заңын табу, гидродинамикада, ағатын сұйық зат жылдамдығының оның бүкіл массасына таралу заңын, яғни жылдамдықтың сүйық зат нүктелері мен уақытқа тәуелділігін табу, физикада электр мен магнетизм өрісінің кернеуін бүкіл кеңістікте табу негізгі басты мәселелер болып табылады, өйткені техникалық мәселелердің көпшілігінің шешілуі осы мәселелерге келіп тіреледі. Мәселен, сүңгуір қайықтың су астында, кемелердің, теңіз беттерінде жүзіп жүруі, снарядтардың, самолеттердің әуеде ұшуы қатты денелердің сүйық зат ішіндегі қозғалысына мысалдар бола алады. Бұлардың құрылыстары және жобаланулары математикалық әдісті, былайша айтқанда дифференциалдық теңдеулер теориясын қолдануды талап етеді.
Тақырыптың өзектілігі:
Математика курстарын оқытуда оқу процесінде дифференциялдық теңдеулер пәнінде қарастырылатын сызықты дифференциалдық теңдеулер жүйесін интегралдаудың матрицалық-векторлық тәсілін қарастыра отырып, математиканы тереңдетіп оқытатын мектептер мен жоғары математиканы өткенде қолдану.
Ғылыми жаңашылдығы:
Бұл дипломдық жобаның жаңалығы- математика курсында оқытылатын теңдеудің жоғары математикада алатын орнын, әсіресе сызықтық дифференциалдық теңдеулердің шешімін табуда кеңінен қолданысын қарастыру.
Жұмыстың практикалық маңыздылығы:
Сызықты дифференциалдық теңдеулер жүйесін интегралдаудың матрицалық-векторлық тәсілінде теорияда алған білімін практикада жүзеге асыру.
Қазіргі ахуалы:
Студенттердің белгілі бір математикалық мәдениетін немесе олардың ғылыми, әсіресе математиканы оқытудың практикалық және қолданбалы бағыттарының мәнін түсіну, сол сияқты математикалық модельдеудің әдістерін меңгеру мен пәнаралық байланыстарды жүзеге асыру іскерлігі сияқты көзқарастырын қалыптастыру тұрғысынан болашақ мұғалімдердің іргелі математикалық дайындықтарына атқарар маңызы зор.
Диплом жұмыстың мақсаты:
Жоғары оқу орындарында оқытылатын дифференциалдық теңдеулерді шешудің әр түрлілігін зерттеу, пәнді оқытуда бірінші, біртекті және сызықты диференциалдық теңдеулер және оларға келтірілетін теңдеулерді шешуді үйрету, математика курсында оқу процесінде пәнаралық байланыстар орнату, теорияда алған білімдерін практикада жүзеге асыру, ұқыптылыққа тәрбиелеу және ойлау қабілеттерін дамыту болып табылады.
Дипломдық жұмыстың міндеттері:
- сызықтық дифференциалдық теңдеулерді шешудің әр түрлілігін анықтау
- бірінші, біртекті және сызықты диференциалдық теңдеулер және оларға келтірілетін теңдеулерді қарастыру
- математика курсында оқу процесінде пәнаралық байланыстарды ұйымдастыру
- сызықтық теңдеулерді шешуде теорияда алған білімдерін практикада іске асыру.
Зерттелу обьектісі:
Жоғары оқу орындарында математика курсында оқытылатын дифференциалдық теңдеулердің шығу тарихы, дифференциалдық теңдеулердің негізі ұғымдары арқылы дифференциалдық теңдеулерді шешуде тиімді жолдарын есептер шығаруда қолдану, математиканың және физика пәндерімен өзара байланысты арттыру, сызықтық дифференциал теңдеулер ұғымы, коэффициенттері тұрақты біртекті емес сызықтық дифференциалдық теңдеулерді және теңдеулер жүйесін шешу жолдарын зерттеу болып табылады
Теориялық және әдістемелік негізі:
Кіріспе, 2 тараудан, қорытындыдан, қолданылған әдебиеттер және аннотациядан тұрады. Кіріспеде дипломдық жұмыстың мақсаты, практикалық маңыздылығы, тақырыптың өзектілігі көрсетілген. 1 тарауда дифференциалдық теңдеулерді шешудің әр түрлі тәсілдерінің теориялары қарастырылды. 2 тарауда біртекті сызықтық дифференциалдық теңдеулерді және теңдеулер жүйесін шешу жолдары,тәсілдері қарастырылып, есеп шығару жолдары көрсетілді
Практикалық базасы:
I.СЫЗЫҚТЫ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІ
Дифференциалдық теңдеудің ұғымдары
Дифференциалдық теңдеу деп тәуелсіз айнымалы х пен ізделінетін ![]() функциясын және оның туындыларын байланыстыратын теңдеуді айтады. Егер теңдеудегі тәуелсіз айнымалы біреу болса, онда теңдеуді жай дифференциалдық теңдеу немесе дифференциалдық теңдеу деп атайды. Егер де тәуелсіз айнымалы саны екеу немесе одан көп болса, онда теңдеуді дербес туындылы дифференциалдық теңдеу деп атайды.
функциясын және оның туындыларын байланыстыратын теңдеуді айтады. Егер теңдеудегі тәуелсіз айнымалы біреу болса, онда теңдеуді жай дифференциалдық теңдеу немесе дифференциалдық теңдеу деп атайды. Егер де тәуелсіз айнымалы саны екеу немесе одан көп болса, онда теңдеуді дербес туындылы дифференциалдық теңдеу деп атайды.
Осы әдістемелік нұсқауда жай дифференциалдық теңдеулерді қарастырамыз.
Дифференциалдық теңдеудің реті деп теңдеудегі туындының ең жоғарғы ретін айтады. Жалпы жағдайда n-ретті дифференциалдық теңдеу төмендегідей жазылады:
![]() (1.1)
(1.1)
Дифференциалдық теңдеудің шешімі деп қайсыбір (а,b) интервалында анықталған, реті дифференциалдық теңдеулердің ретіндей болатын туындылары үзіліссіз және х бойынша ![]() теңдеуді тепе-теңдікке айналдыратын
теңдеуді тепе-теңдікке айналдыратын ![]() функциясын айтады.
функциясын айтады.
Мысалы, егер![]() ,
, ![]() функциясы (1.1) теңдеудің шешімі болса, онда
функциясы (1.1) теңдеудің шешімі болса, онда
![]()
Егер (1) теңдеу туындының жоғарғы ретіне қарай шешілсе:
![]() (1.2)
(1.2)
онда дифференциалдық теңдеу нормалды түрде берілген деп айтады.
Егер (1.2) теңдеудің оң жағындағы өрнек белгісіз функция мен оның туындыларына қарай сызықтық және олардың көбейтінділерін қамтымаса, онда мұндай теңдеулерді сызықтық дифференциалдық теңдеулер деп атайды.
Дифференциалдық теңдеу шешімінің графигін теңдеудің интегралдық қисығы деп атайды.
Берілген дифференциалдық теңдеудің шешімін табу процесін теңдеуді интегралдау деп атайды.
n-ретті дифференциалдық (1.1) теңдеудің жалпы шешімі деп тәуелсіз айнымалы х тен және кез келген п тұрақты саннан тәуелді
![]() (1.3)
(1.3)
функциясын айтады. (1.3) жалпы шешім қайсыбір жағдайларда айқындалмаған
![]() (1.3)
(1.3)
түрде алынады, бұл шешімді жалпы интеграл деп атайды.
Дифференциалдық теңдеудің дербес шешімі деп жалпы шешімнен тұрақтылардың белгілі бір мәндерінде алынған шешімді айтады. (1.2) дифференциалдық теңдеудің дербес шешімін табу үшін бастапқы шарттар беріледі:
![]()
1.1 Біртекті сызықты теңдеулер жүйесі
Бірінші тарауда дифференциалдық теңдеулердің сызықты жүйелерінің негізгі ұғымдары және олардың шешімдері қарастырылады.
Біздің қарастыратын жүйеміз мынадай:
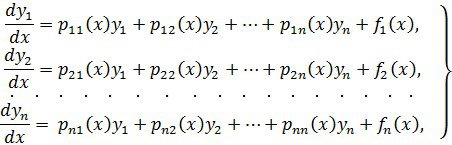
мұндағы ![]() ( k, l
( k, l ![]() ) және
) және ![]() ( k
( k ![]() ) мәні
) мәні ![]() -тан берілген функциялар, онда ол дифференциалдық теңдеулердің сызықты жүйесі немесе, қысқаша, сызықты жүйе деп аталады.
-тан берілген функциялар, онда ол дифференциалдық теңдеулердің сызықты жүйесі немесе, қысқаша, сызықты жүйе деп аталады.
![]() (k
(k![]() ). (1.4)
). (1.4)
Егер барлық функциялар (a,b) аралығында ![]() 0 болса, онда (1.1) жүйе біртекті деп аталады. Бұл жағдайда (1.1) жүйе мына түрде жазылады:
0 болса, онда (1.1) жүйе біртекті деп аталады. Бұл жағдайда (1.1) жүйе мына түрде жазылады:
![]() (k
(k![]() ) (1.5)
) (1.5)
1. (1.1) сызықты жүйе тәуелсіз айнымалының кез-келген өзгертулерінде сызықты болып қалады
![]() ,
,
мұндағы ![]() – t-дан кез-келген функция, (α,β) интервалында анықталған және үзіліссіз дифференциалданған, сонымен бірге барлық (α,β) интервалында
– t-дан кез-келген функция, (α,β) интервалында анықталған және үзіліссіз дифференциалданған, сонымен бірге барлық (α,β) интервалында ![]() ,
, ![]() .
.
Шыныменде,
![]()
Сондықтан (1)жүйе мына түрге келеді
![]() (k
(k![]() ),
),
мұндағы
![]()
![]()
![]() коэфициенттері және
коэфициенттері және ![]() функциялары (α,β) интервалында үзіліссіз. Бұдан басқа, біртекті жүйе біртектіге айналатыны белгілі.
функциялары (α,β) интервалында үзіліссіз. Бұдан басқа, біртекті жүйе біртектіге айналатыны белгілі.
Тәуелсіз айнымалыны алмастырып, n-ші ретті сызықты теңдеу сияқты, осы сызықты жүйені ыңғайлы түрге алып келуге болады .
2. (1.1) сызықты жүйе сызықты болып қалады егер, қандай да болсын белгісіз функциялар
![]() (1.6)
(1.6)
![]() түрлендірулер коэфициенттері, мазмұны (α,β) интервалында x-тан үзіліссіз дифференциалданған функциялар.
түрлендірулер коэфициенттері, мазмұны (α,β) интервалында x-тан үзіліссіз дифференциалданған функциялар.
Шыныменде, (1.3) түрлендіру ерекше болмағандықтан, онда жалғыз кері түрлендіру бар болады
![]() (i
(i![]() ), (1.7)
), (1.7)
мұндағы![]() - (a,b) аралығында үзіліссіз дифференциалданған. (1.7) түрлендіру де ерекше болып табылмайды, ал оның
- (a,b) аралығында үзіліссіз дифференциалданған. (1.7) түрлендіру де ерекше болып табылмайды, ал оның ![]() коэфициенттерін танымал Крамер ережесін пайдаланып табуға болады. Сонымен бірге
коэфициенттерін танымал Крамер ережесін пайдаланып табуға болады. Сонымен бірге ![]() коэфициенттері
коэфициенттері ![]() коэфициенттері арқылы мына формуламен айқындалады:
коэфициенттері арқылы мына формуламен айқындалады:
![]() (
(![]() k
k![]() ).
).
Мұндағы ![]() -
-![]() анықтайтын
анықтайтын![]() элементінің алгебралық толықтауышы.
элементінің алгебралық толықтауышы.
Енді жүйенің түрлендірілген түрін табайық. Бізде бары
![]()
![]()
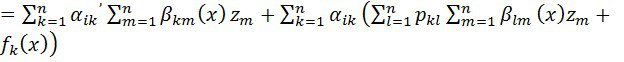
немесе
![]() (i
(i![]() ), (1.8)
), (1.8)
мұндағы
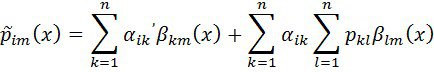
(![]() m
m![]() ),
),
![]() (i
(i![]() ).
).
(1.8) жүйенің түрлендірілген коэфициенттері (a,b) аралығында үзіліссіз және де біртекті жүйе біртекті болып өзгереді.
1.1.1 Біртекті жүйесінің шешімдерінің негізігі қасиеттері
Біздің нақты тапсырмамыз (1.5) жүйені шешу жолдарын қарастыру. Бірақ бұл тапсырманы шешу үшін, n-ші ретті біртекті сызықтық теңдеу сияқты, кейде бірінші кейбір комплекстік шешімдерін табу ыңғайлылырақ. (1.5) Біртекті жүйенің комплекстік шешімі туралы ұғым енгізейік.
Комплекстік функцияның қосындысын нақты ауыспалыдан қарастырайық
![]() =
=![]() +
+ ![]() (1.9)
(1.9)
Мұндағы ![]() (k
(k![]() )
) ![]() нақты ауыспалыдан нақты функция болып табылады.
нақты ауыспалыдан нақты функция болып табылады.
(1.9) функцияның жиынтығын (a,b) аралығында біртекті жүйенің (1.5) комплекстік шешімі деп атаймыз, егер бұл функциялар a![]() тепе-теңдігі үшін барлық жүйелердің теңдіктерін қарастырса, яғни
тепе-теңдігі үшін барлық жүйелердің теңдіктерін қарастырса, яғни
![]() (k
(k![]() )
)
немесе
![]() + I
+ I ![]() + I
+ I ![]() (1.10)
(1.10)
(k![]() ).
).
Екі комплекс сандар өрісі бір-бірінің арасында өзара тең, тек сәйкесінше нақты және жорамал бөліктері тең болса. Олай болса, (1.10) тепе-теңдікте нақты және жорамал бөліктерін теңестіріп көреміз, егер (1.5) жүйе (1.9) комплекстік шешімге ие болса, онда оның екі нақты шешімі болады
![]() (
(![]() ) ,
) ,
![]() (
(![]() ) ,
) ,
яғни функцияның нақты және жорамал бөліктері (1.5) біртекті сызықтық жүйенің (1.9)комплекстік шешімін құрушы, осы жүйеге екі нақты шешім құрады.
Біртекті сызықтық жүйенің шешімі (1.5) келесі қасиеттерге ие болады, n-ші ретті біртекті сызықтық теңдеуді ұқсастық қасиеттерімен шешу.
1. Егер
![]() (k
(k![]() ) (1.11)
) (1.11)
(2) біртекті сызықтық жүйенің шешімі бар, онда
![]() (k
(k![]() ) , (1.12)
) , (1.12)
Мұндағы C – тұрақты сан, ол да осы жүйенің шешімі болады, біртекті сызықтық жүйелердің шешімін құрушы, тұрақты біреуіне барлық функцияларды көбейтіп,біз тағыда шешімін аламыз.
Шынымен, (1.12) функцияны (1.5) жүйеге қойып,
(![]() )
) ![]()
![]() C
C ![]()
![]() (
(![]() ) (1.13)
) (1.13)
аламыз.
С-ға қысқартып, біз тепе-теңдік аламыз, (1.11) функция (1.5) жүйенің шешімі болғандықтан. Сондықтан (1.13) теңдік тепе-тең орындалады, дәлелдеу керегі де осы еді.
2. (1.5) жүйенің шешімі m болсын
![]()
![]() ( k
( k![]() ) ,
) ,
![]() ( k
( k![]() ) ,
) ,
. . . . . . . . . . (1.14)
![]() ( k
( k![]() ) .
) .
Мұндағы бірінші индекс шешімнің номерін білдіреді, ал екіншісі – функцияның номері.
Дәлелдейік, шешімнің (1.14) сызықтық тәсілі кез-келген тұрақты коэфициенттерімен
![]() ,
, ![]() , … ,
, … , ![]() , яғни функцияның жиыны
, яғни функцияның жиыны
![]()
![]() (k
(k![]() ) (1.15)
) (1.15)
бұл да (1.5) жүйенің шешімі болады.
Шыныменде, (1.15)-і (1.5)-ге қойып, мынаны аламыз
( ![]() )
) ![]()
![]()
![]() (
( ![]() ) ( k
) ( k![]() ) (1.16)
) (1.16)
немесе
![]()
![]()
![]()
![]() ) ( k
) ( k![]() ). (1.17)
). (1.17)
Тепе-теңдік орынға ие болғандықтан
![]()
![]()
![]()
![]()
![]() ( k
( k![]() ), (1.18)
), (1.18)
(2) жүйеге ![]() -нің шешімін қойған, нәтижесі (14) теңдік болып табылады, сәйкесінше, (13) теңдік те тепе-тең орындалады, біздің дәлелдеу керегіміз де осы еді.
-нің шешімін қойған, нәтижесі (14) теңдік болып табылады, сәйкесінше, (13) теңдік те тепе-тең орындалады, біздің дәлелдеу керегіміз де осы еді.
Енді бізге (2) біртекті жүйедегі n-нің жеке шешімі белгілі екенін болжайық. Басты сұрақ қойайық: қандай жағдайда сызықтық әрекет осылардың шешімдерінің негізсіз тұрақты коэфициенттерімен ![]() ,
, ![]() , … ,
, … , ![]() біртекті жүйенің жалпы шешімін береді.
біртекті жүйенің жалпы шешімін береді.
Қойылған сұраққа жауап беру үшін, сызықты тәуелсіз жүйенің функциясы ұғымын енгіземіз.
1.1.2 Остроградский – Лиувилль– Якоби формуласы
Сызықты тәуелсіз жүйенің функциясы ұғымы.
Функциялардағы m жүйесін қарастырайық:
![]()
![]() ( k
( k![]() ) ,
) ,
. . . . . . . . . (16)
![]() ( k
( k![]() ) .
) .
Бұл жүйелер (a,b) аралығында сызықты тәуелсіз деп аталады, егер ![]() ,
,![]() ... ,
... , ![]() сандары жоқ болса, біруақытта нөлге тең емес, осы жағдайда барлық (a,b) интервалында мына теңдік орындалатын еді:
сандары жоқ болса, біруақытта нөлге тең емес, осы жағдайда барлық (a,b) интервалында мына теңдік орындалатын еді:
![]() ( k
( k![]() ) (17)
) (17)
яғни егер функцияның ешқандай сызықтық әрекеті (16) таблицаның әрбір бағанына, біреуімен ғана барлық бағандарға ![]() ,
,![]() ... ,
... , ![]() тұрақты коэфициенттерімен, (a,b) интервалында нөлге тең емес немесе , (16) таблицаның бірде-бір бағаны (a,b) интервалында жатпаса, басқа барлық бағандарда сызықтық әрекет орындалады. Қарсы жағдайда (16) жүйелер (a,b) аралығында сызықты тәуелді деп аталады.
тұрақты коэфициенттерімен, (a,b) интервалында нөлге тең емес немесе , (16) таблицаның бірде-бір бағаны (a,b) интервалында жатпаса, басқа барлық бағандарда сызықтық әрекет орындалады. Қарсы жағдайда (16) жүйелер (a,b) аралығында сызықты тәуелді деп аталады.
Сонымен қатар, функцияның екі жүйесі
![]() ( k
( k![]() ) ,
) ,
![]() ( k
( k![]() )
)
(a,b) интервалында сызықты тәуелсіз болады, егер мына қатынастар болмаса:
![]()
![]()
![]() (18)
(18)
![]() болғанда, осыған орай ескергеніміз жөн, (18) кірген барлық байланыстар, (a,b) интервалының барлық нүктелерінде анықталған.
болғанда, осыған орай ескергеніміз жөн, (18) кірген барлық байланыстар, (a,b) интервалының барлық нүктелерінде анықталған.
Шыныменде, егер (16) функцияның бір жүйесі функциядан тұрса, (a,b) интервалында тепе-теңдік нөлге тең, онда бұл фукцияның жүйелері (a,b) аралығында сызықты тәуелді.
Шыныменде, мейлі, мысалы,
(a,b) аралығында ![]()
![]()
Онда кез-келген ![]() және
және ![]() болғанда (a,b) интервалында (14) арақатынас орындалады, а бұл (16) функцияның жүйелері (a,b) аралығында сызықты тәуелді екенін білдіреді.
болғанда (a,b) интервалында (14) арақатынас орындалады, а бұл (16) функцияның жүйелері (a,b) аралығында сызықты тәуелді екенін білдіреді.
1 Мысал. Функцияның жүйелері
![]()
![]()
![]()
![]()
(![]() ,
,![]() ) аралығында сызықты тәуелсіз.
) аралығында сызықты тәуелсіз.
2 Мысал. ![]() ,
,![]() қос-қостан түрлі сандар деп болжайық ( нақты немесе комплекстік). Онда функцияның жүйесі
қос-қостан түрлі сандар деп болжайық ( нақты немесе комплекстік). Онда функцияның жүйесі
![]() ,
, ![]() , … ,
, … , ![]() ,
,
![]() ,
, ![]() , … ,
, … , ![]() ,
,
. . . . . . . . . . . . (19)
![]() ,
, ![]() , … ,
, … , ![]() ,
,
Әрбір жолда ![]() коэфициенттерінен ең болмағанда біреуі нөлден өзгеше, (
коэфициенттерінен ең болмағанда біреуі нөлден өзгеше, (![]() ,
,![]() ) интервалында сызықты тәуелсіз.
) интервалында сызықты тәуелсіз.
3 Мысал. Функцияның жүйелері
![]()
![]()
![]()
![]()
(![]() ,
,![]() ) аралығында сызықты тәуелді.
) аралығында сызықты тәуелді.
4 Мысал. Функцияның жүйелері
![]()
![]()
![]()
![]()
(![]() ,
,![]() ) аралығында сызықты тәуелсіз.
) аралығында сызықты тәуелсіз.
5 Мысал. Функцияның жүйелері
![]()
![]()
![]()
![]()
(![]() ,
,![]() ) аралығында сызықты тәуелді.
) аралығында сызықты тәуелді.
Сызықты тәуелді n жүйесі функциясының қажетті шарттары
Бізде функцияның n жүйесі бар болсын:
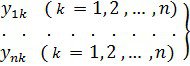 (20)
(20)
Қарастырылымға анықтауыш енгізейік
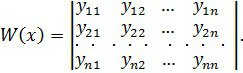
Бұл анықтауыш (20) функциялар жүйесі үшін Вронский анықтауышы немесе бұл функциялар жүйесінің вронскианы деп аталады.
Т е о р е м а. Егер (20) функцияның ![]() жүйесі
жүйесі ![]() интервалында сызықты тәуелді болса, онда
интервалында сызықты тәуелді болса, онда![]() аралығында
аралығында ![]() .
.
Расында, бізде мына арақатынас бар
![]() 0 ( k
0 ( k![]() ), (21)
), (21)
мұнда ![]() барлығы нөлге тең емес.
барлығы нөлге тең емес.
(21) жүйені ![]() қатысты алгебралық теңдеулердің біртекті сызықты жүйесі ретінде қарастыра отырып, нөлдік емес шешімі бар екенін көріп тұрмыз, ал сондықтан, алгебрадан анық екені белгілі, бұл жүйенің анықтауышы нөлге тең. Бірақ бұл анықтауыш вронскиан болып табылады, сондықтан соңғысы
қатысты алгебралық теңдеулердің біртекті сызықты жүйесі ретінде қарастыра отырып, нөлдік емес шешімі бар екенін көріп тұрмыз, ал сондықтан, алгебрадан анық екені белгілі, бұл жүйенің анықтауышы нөлге тең. Бірақ бұл анықтауыш вронскиан болып табылады, сондықтан соңғысы ![]() интервалының барлық нүктелерінде нөлге айналуы керек.
интервалының барлық нүктелерінде нөлге айналуы керек.
n теңдеуінің біртекті сызықты жүйесінің сызықты тәуелсіз n шешімдерінің қажетті және жеткілікті шарттары
Енді (20) функцияның жүйесінің әрқайсысы (2) жүйенің шешімі болсын, олай болса бізде ![]() шешімдері бар:
шешімдері бар:
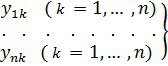 (22)
(22)
Т е о р е м а. Егер (22) ![]() шешімдері
шешімдері ![]() интервалында сызықты тәуелсіз болса, ондағы
интервалында сызықты тәуелсіз болса, ондағы ![]() анықталған және үзіліссіз, онда олардың вронскианы осы интервалдың кез-келген нүктелерінде нөлге айналмайды.
анықталған және үзіліссіз, онда олардың вронскианы осы интервалдың кез-келген нүктелерінде нөлге айналмайды.
Қарама-қарсы жағдайын болжайық. ![]() болсын, әрі
болсын, әрі ![]()
![]() теңдеулерінің жүйесін құрастырайық
теңдеулерінің жүйесін құрастырайық
![]() 0 ( k
0 ( k![]() (23)
(23)
мұндағы ![]() (23) жүйенің анықтауышы нөлге тең, ол
(23) жүйенің анықтауышы нөлге тең, ол ![]() тең болғандықтан. Сондықтан (23) жүйеде нөлдік шешім болады
тең болғандықтан. Сондықтан (23) жүйеде нөлдік шешім болады
![]()
![]() болғанда (12) формуланы пайдаланып, енді шешімін құрастырайық
болғанда (12) формуланы пайдаланып, енді шешімін құрастырайық
![]() (24)
(24)
![]() (23) жүйені қанағаттандыратын болғандықтан, белгілі, (24) шешім
(23) жүйені қанағаттандыратын болғандықтан, белгілі, (24) шешім ![]() нүктесінде нөлдік бастапқы мағынасы бар.
нүктесінде нөлдік бастапқы мағынасы бар.
![]() болғанда
болғанда ![]()
![]()
Бірақ жалғыздық теоремасына қарап (24) шешім нөлдік болып табылады, ![]()
![]() , сондықтан мына тепе-теңдікті аламыз
, сондықтан мына тепе-теңдікті аламыз
![]()
![]()
мұндағы барлық ![]() нөлге тең емес, яғни (22) шешім
нөлге тең емес, яғни (22) шешім ![]() интервалында сызықты тәуелді, болжамға қарамастан. Теорема дәлелденді.
интервалында сызықты тәуелді, болжамға қарамастан. Теорема дәлелденді.
Дәлелденген теоремаға және алдыңғы тараудағы теоремаға тиісті, (2) жүйенің ![]() шешімі
шешімі ![]() интервалында сызықты тәуелсіз болу үшін, қажетті және жеткілікті, олардың вронскианы осы интервалдың нүктелерінің әрқайсысында нөлге тең болмауы қажет.
интервалында сызықты тәуелсіз болу үшін, қажетті және жеткілікті, олардың вронскианы осы интервалдың нүктелерінің әрқайсысында нөлге тең болмауы қажет.
Алайда (2) жүйенің сызықты тәуелсіз ![]() шешімін құру үшін,
шешімін құру үшін,![]()
![]() интервалының ең болмағанда бір нүктесінде нөлден өзгеше екеніне көз жету жеткілікті. Бұл келесі екі тамаша вронскиан (2) жүйенің
интервалының ең болмағанда бір нүктесінде нөлден өзгеше екеніне көз жету жеткілікті. Бұл келесі екі тамаша вронскиан (2) жүйенің ![]() шешімі қасиеттерінен туындайды.
шешімі қасиеттерінен туындайды.
1. Егер ![]()
![]() интервалының ең болмағанда бір нүктесінде нөлге айналса, яғни (2) жүйенің коэфициенттерінің үзіліссіз интервалы, онда
интервалының ең болмағанда бір нүктесінде нөлге айналса, яғни (2) жүйенің коэфициенттерінің үзіліссіз интервалы, онда ![]() осы интервалдың барлық нүктелерінде нөлге тең.
осы интервалдың барлық нүктелерінде нөлге тең.
2. Егер ![]()
![]() интервалының ең болмағанда бір нүктесінде нөлге тең емес болса, онда ол
интервалының ең болмағанда бір нүктесінде нөлге тең емес болса, онда ол ![]() интервалының кез-келген нүктесінде нөлге айналмайды.
интервалының кез-келген нүктесінде нөлге айналмайды.
Осылайша, (2) жүйенің ![]() шешімі
шешімі![]() интервалында сызықты тәуелсіз болу үшін,қажетті және жеткілікті, олардың вронскиі осы интервалдың ең болмағанда бір нүктесінде нөлден өзгеше болуы керек.
интервалында сызықты тәуелсіз болу үшін,қажетті және жеткілікті, олардың вронскиі осы интервалдың ең болмағанда бір нүктесінде нөлден өзгеше болуы керек.
Жоғарыда көрсетілген (2) біртекті жүйені вронскиана қасиетімен шешуі келесі тамаша формуладан оңай шығады, жүйенің вронскиан шешімін диагоналдық коэфициенттері арқылы табады.
![]() (17)
(17)
![]() -дің (a,b) интервалында кез-келген нүктесі бар.
-дің (a,b) интервалында кез-келген нүктесі бар.
Осы формуланы дәлелдеу үшін, бағандар арқылы дифференциалдап, туындыны вронскианадан есептеп шығарамыз. Бұл жағдайда туынды n-ші ретті анықтауыштан, n-ші анықталатын соммаға тең, осыдан пайда болған элементтерді 1-ші,2-ші, ... , n-ші бағандарды олардың туындыларымен кезек-кезекпен ауыстырады
![]()
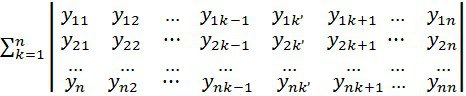
Онда, ![]() ,
,![]() , ... ,
, ... ,![]() оң жақтағы туындыларды ауыстырып , m=n болғанда олардың тепе-теңдік мағынасымен (12), мынаны аламыз
оң жақтағы туындыларды ауыстырып , m=n болғанда олардың тепе-теңдік мағынасымен (12), мынаны аламыз
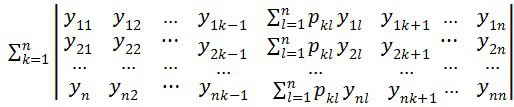
Сомма белгісінің астындағы анықтауышты n анықтайтын соммаға қойайық. Барлық табылған анықтағыштар 0-ге тең болады, ![]() болатын анықтауыштан басқа.
болатын анықтауыштан басқа.![]() -ға сәйкес анықтауыш
-ға сәйкес анықтауыш ![]() –қа тең, Сондықтан
–қа тең, Сондықтан
![]() ,
,
Осыдан (25) формула шығады.
1.1.3 жалпы шешімін құру
Шешімдердің фундаментальді жүйесі туралы ұғым.
Біртекті (2) жүйенің ![]() шешімінің құрамы деп,
шешімінің құрамы деп, ![]() интервалында анықталған және сызықты тәуелсіз,осы интервалда шешімдердің фундаментальді жүйесі деп аталады.
интервалында анықталған және сызықты тәуелсіз,осы интервалда шешімдердің фундаментальді жүйесі деп аталады. ![]() шешімдердің жүйесі
шешімдердің жүйесі ![]() интервалында шешімдердің фундаментальді жүйесі болады егер, осы шешімдердің вронскианы
интервалында шешімдердің фундаментальді жүйесі болады егер, осы шешімдердің вронскианы ![]() интервалының ең болмағанда бір нүктесінде нөлден өзгеше болғанда ғана.
интервалының ең болмағанда бір нүктесінде нөлден өзгеше болғанда ғана.
Фундаментальді жүйенің шешімі бар туралы теорема
Егер (2) жүйенің коэфициенттері (a,b) интервалында үзіліссіз болса, онда шешімнің фундаментальді жүйесі болады. Осы интервалда анықталған және үзіліссіз.
Шыныменде, (a,b) аралығынан ![]() нүктесін алайық және n шешімді Пикара тәсілімен орналастырайық
нүктесін алайық және n шешімді Пикара тәсілімен орналастырайық
![]() ( k
( k![]() ) ,
) ,
![]() ( k
( k![]() ) ,
) ,
. . . . . . . (18)
![]() ( k
( k![]() ) .
) .
Осы нүктедегі келесі бастапқы мағыналарымен:
![]()
![]() ,
, ![]() , … ,
, … , ![]()
![]() болғанда,
болғанда,
![]() ,
, ![]() , … ,
, … , ![]()
![]() болғанда,
болғанда,
. . . . . . . . . . . . . . .
![]() ,
, ![]() , … ,
, … , ![]()
![]() болғанда.
болғанда.
![]() нүктесінде (18) вронскиан шешімі бірге тең. Сәйкесінше, жүйенің шешімі – фундаментальді .
нүктесінде (18) вронскиан шешімі бірге тең. Сәйкесінше, жүйенің шешімі – фундаментальді .
Теореманы дәлелдеу кезінде 1 мен 0 сандарының орнына кез-келген ![]() сандарын алуға болады, осылардағы анықтауышы 0 емес. Фундаментальді жүйенің сандық емес көп шешімі бар екені белгілі.
сандарын алуға болады, осылардағы анықтауышы 0 емес. Фундаментальді жүйенің сандық емес көп шешімі бар екені белгілі.
Орнатылған (18) фундаментальді жүйе ![]() нүктесінде нормаланған деп аталады. Пайда болу және жекелеген теоремаларына тиісті, (a,b) аралығындағы
нүктесінде нормаланған деп аталады. Пайда болу және жекелеген теоремаларына тиісті, (a,b) аралығындағы ![]() нүктелерінің әрқайсысына осы нүктеде тек бір ғана нормаланған шешімнің фундаментальді жүйесі болады.
нүктелерінің әрқайсысына осы нүктеде тек бір ғана нормаланған шешімнің фундаментальді жүйесі болады.
![]() –ші ретті біртекті сызықты теңдеу сияқты, шешімдердің фундаментальді жүйесін білу, (2) жүйенің жалпы шешімін құруға көмектеседі.
–ші ретті біртекті сызықты теңдеу сияқты, шешімдердің фундаментальді жүйесін білу, (2) жүйенің жалпы шешімін құруға көмектеседі.
Н е г і з г і т е о р е м а. Егер ![]() интервалында (2) біртекті сызықты жүйенің (26) шешімдерінің фундаментальді жүйесі болса, онда формулалар
интервалында (2) біртекті сызықты жүйенің (26) шешімдерінің фундаментальді жүйесі болса, онда формулалар
![]()
![]() (27)
(27)
мұндағы ![]() – ерікті тұрақты, мына облыстарда жүйенің жалпы шешімін береді
– ерікті тұрақты, мына облыстарда жүйенің жалпы шешімін береді
![]()
![]() (28)
(28)
яғни (2) жүйенің тапсырмасының барлық облыстарында.
Шыныменде, (27) жүйе ерікті тұрақты![]() қатысты (28) облыста шешілетін, өйткені (27) сызықты жүйе болады, оның анықтауышы
қатысты (28) облыста шешілетін, өйткені (27) сызықты жүйе болады, оның анықтауышы ![]() тең бола тұра, нөлден өзгеше, (26) шешімдердің фундаментальді жүйесі болғандықтан.
тең бола тұра, нөлден өзгеше, (26) шешімдердің фундаментальді жүйесі болғандықтан.
Бұдан басқа, біртекті сызықты жүйенің шешімінің екінші қасиетіне байланысты (27) функцияның жиынтығы (2) жүйенің шешімі болып табылады, ерікті тұрақты![]() барлық мағыналарында.
барлық мағыналарында.
Сондықтан, дифференциалдық теңдеулердің нормальді жүйесінің жалпы шешімі анықтамасына сәйкес, (27) функцияның жиынтығы (28) облыста (2) жүйенің жалпы шешімі болып табылады.
(27) формула (2) жүйенің барлық шешімдерін өзінде қамтиды.
Меншікті шешімін табу үшін, бастапқы талаптарды қанағаттандыратын:
![]() болғанда
болғанда ![]() (29)
(29)
мұндағы ![]() – (28) облыстағы кез-келген нүкте, (27) жүйеге бастапқы мәліметтерді қою керек. Мынаны аламыз
– (28) облыстағы кез-келген нүкте, (27) жүйеге бастапқы мәліметтерді қою керек. Мынаны аламыз
![]()
![]() (30)
(30)
Бұл жүйені ![]() қатысты шеше отырып, мынаны аламыз:
қатысты шеше отырып, мынаны аламыз:
![]()
Бұл ![]() мағыналарын (27) жалпы шешімге қойып, табамыз
мағыналарын (27) жалпы шешімге қойып, табамыз
![]() . (31)
. (31)
Бұл ізделініп отырған шама. Дәл сондай бастапқы (29) шарттарымен басқа шешімдер жоқ.
![]() тұрақтылары, (30) жүйеден анықталған, сызықты жүйелер болып табылады
тұрақтылары, (30) жүйеден анықталған, сызықты жүйелер болып табылады ![]() бастапқы мағыналарынан,
бастапқы мағыналарынан, ![]() ізделінетін функцияларынан. Бұл функциялар айрықша жай болады, егер шешімдердің фундаментальді жүйесі
ізделінетін функцияларынан. Бұл функциялар айрықша жай болады, егер шешімдердің фундаментальді жүйесі ![]() нүктесінде нормаланған болса.
нүктесінде нормаланған болса.
Шынында, бұл жағдайда (30) жүйе мына түрге келеді
![]()
![]()
Сондықтан, (27) жалпы шешімінің формуласын қолданып, аламыз,(29) бастапқы шарттарымен шешімі мына формуламен беріледі
![]()
![]()
Осы формуланы (2) жүйенің Коши түрінде жалпы шешімі ретінде де қарастыруға болады, егер ![]() бастапқы мағыналарын ерікті деп санасақ.
бастапқы мағыналарын ерікті деп санасақ.
(2) біртекті жүйесінің n шешімдерінің сызықты комбинациясы ![]() ерікті тұрақты коэфициенттерімен бірге жалпы шешімін беру үшін, қажетті және жеткілікті, бұл шешімдер сызықты тәуелсіз болу керек, яғни олар шешімдердің фундаментальді жүйесін құру керек.
ерікті тұрақты коэфициенттерімен бірге жалпы шешімін беру үшін, қажетті және жеткілікті, бұл шешімдер сызықты тәуелсіз болу керек, яғни олар шешімдердің фундаментальді жүйесін құру керек.
1.2 Біртекті емес сызықты теңдеулер жүйесі
1.1.1 Біртекті емес жүйенің ортақ шешімінің құрылымы
Біртекті емес жүйені қарастырайық
![]()
![]() (1)
(1)
Бізге осы жүйенің кейбір дербес шешімдері белгілі деп, болжап көрейік
![]()
![]()
сондықтан бізде мына тепе-теңдік бар
![]()
![]() (2)
(2)
Формулаларға жаңа ![]() белгісіз фукцияларды енгіземіз
белгісіз фукцияларды енгіземіз
![]()
![]()
(3) фукцияларды (1) біртекті емес жүйеге қойып, аламыз
![]()
![]()
Осыдан, (2) тепе-теңдікке қарап, ![]() функциясына келесі дифференциалдық теңдеулердің біртекті жүйесін аламыз:
функциясына келесі дифференциалдық теңдеулердің біртекті жүйесін аламыз:
![]()
![]() (4)
(4)
Бұл жүйе (1) біртекті емес жүйеге сәйкес,біртекті жүйе деп аталады.
(4) біртекті жүйенің жалпы шешімі мына формуламен беріледі
![]()
![]() (5)
(5)
мұндағы ![]()
![]() осы біртекті жүйенің кейбір шешімдерінің фундаментальді жүйесі.
осы біртекті жүйенің кейбір шешімдерінің фундаментальді жүйесі.
(5)-ті (3)-ке қойып, аламыз
![]() (6)
(6)
(1)жүйенің барлық шешімдері (6) формуланың ішінде бар. Бұл формула (1) жүйенің жалпы шешімі болып табылады, мына облыстарда
![]()
![]() (7)
(7)
яғни (1) жүйенің тапсырмасының барлық облыстарында.
Осылайша, (1) біртекті емес жүйесінің жалпы шешімін табу үшін, осы жүйенің қандай да бір дербес шешімін табу жеткілікті және оған (4) біртекті жүйеге сәйкес жалпы шешімін қосу керек.
1.2.2 Тұрақты ерік түрлендіру әдісі ( Лагранж әдісі)
Т е о р е м а. Егер (4) біртекті жүйенің шешімінің фундаментальді жүйесі белгілі болса, онда (1) біртекті емес жүйенің жалпы шешімін квадратур арқылы табу мүмкін.
Осы теореманы дәлелдеу үшін ерікті тұрақты вариация тәсілін пайдаланайық.
(1) біртекті емес жүйенің шешімін мына түрде іздейік
![]()
![]() (8)
(8)
мұндағы ![]()
![]() (4) біртекті жүйенің шешімдерінің фундаментальді жүйесі, ал
(4) біртекті жүйенің шешімдерінің фундаментальді жүйесі, ал ![]()
![]() –
– ![]() -тан кейбір үзіліссіз дифференциалданған функциялар. Бұл функцияларды (8) формула (1) жүйенің шешімін беретіндей етіп таңдап алайық.
-тан кейбір үзіліссіз дифференциалданған функциялар. Бұл функцияларды (8) формула (1) жүйенің шешімін беретіндей етіп таңдап алайық.
(7)-ні (1)-ге қойып, аламыз
![]()
![]()
немесе
![]()
![]()
Бұл теңдіктерді мына түрде көшіріп алып
![]()
![]()
және ![]()
![]() (4) біртекті жүйенің шешімдерінің фундаментальді жүйесі екенін көңілге алып, біз
(4) біртекті жүйенің шешімдерінің фундаментальді жүйесі екенін көңілге алып, біз ![]()
![]() анықтау үшін,келесі бірінші ретті дифференциалдық теңдеулер жүйесіне келеміз:
анықтау үшін,келесі бірінші ретті дифференциалдық теңдеулер жүйесіне келеміз:
![]()
![]() .
.
Бұл жүйе![]() -ке қатысты шешілетін. Мынаны аламыз
-ке қатысты шешілетін. Мынаны аламыз
![]()
![]() .
.
Интегралдап, табамыз
![]()
![]()
![]() мағыналарын (6) формулаға қойып, (1) жүйенің шешімін мына түрде табамыз
мағыналарын (6) формулаға қойып, (1) жүйенің шешімін мына түрде табамыз
![]()
![]() (10)
(10)
Мұнда ![]() деп болжап, мына шешімді аламыз
деп болжап, мына шешімді аламыз
![]()
![]()
сондықтан (10) жүйені (6) түрде жазуға болады және, сәйкесінше, (10) формуламен анықталатын шешімі,(7) облыста (1) біртекті емес жүйенің шешімі болып табылады. Теорема дәлелденді.
II. БІРТЕКТІ СЫЗЫҚТЫ ЖҮЙЕЛЕРДІ МАТРИЦАЛЫҚ ӘДІСПЕН ИНТЕГРАЛДАУ
2.1 Матрица теориясынан кейбір мәліметтер
Біртекті сызықты жүйені қарастырайық
![]() (
(![]() ) . (1)
) . (1)
Болжап көрейік, ![]() (
(![]() ) коэфициенттері (a,b) интервалында үзіліссіз. Онда (1) жүйе шешімдерінің фундаментальді жүйесі бар, оны келесі таблица түрінде жазуға болады:
) коэфициенттері (a,b) интервалында үзіліссіз. Онда (1) жүйе шешімдерінің фундаментальді жүйесі бар, оны келесі таблица түрінде жазуға болады:
![]()
![]()
![]()
. . . . . . . . (2)
![]()
немесе
![]() (
(![]() ),
),
мұндағы барлық функциялар анықталған және (a,b) аралығында үзіліссіз.
(2) кестеде функцияның әрқайсысы белгіленген орында тұр, олар екі индекспен анықталған. Бірінші индекс жолдың номерін (шешімнің номерін), ал екінші индекс баған номерін (ілделініп отырған функцияның номерін) білдіреді. Және де біз оның құрамына кіретін функциялардың орнын өзгертпей, (2) кестені жалпы біртұтас ретінде қарастыруымыз керек. Сондай кестені матрица деп атайды.
n-ретті квадрат матрица деп
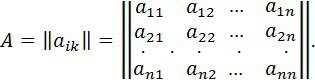
түрде берілген кестені айтамыз.
Шамасы
![]()
Aматрицасының элементтері деп аталатын, рет-ретімен қатаң нақты орналастырылған сандар немесе функциялардың мәні. Бұл рет екі индекспен көрсетіледі, бірінші индекс жолдың номерін, ал екіншісі- бағанның номерін білдіреді, қиылысуларында қарастырылып отқан матрицаның элементі тұр.
![]() матрицасынан біз барлық элементтері a-ға тең екенін түсінеміз. Сондай-ақ
матрицасынан біз барлық элементтері a-ға тең екенін түсінеміз. Сондай-ақ ![]() – барлық элементтері нөлге тең матрица. Ол нөлдік матрица деп аталады.
– барлық элементтері нөлге тең матрица. Ол нөлдік матрица деп аталады.
A матрицасының біртұтас оң дәрежесі
![]() матрицасының біртұтас оң дәрежесі рекурентті байланыспен анықталады
матрицасының біртұтас оң дәрежесі рекурентті байланыспен анықталады
![]()
![]() матрицасының 0 дәрежесі A реті сияқты жалғыз матрицаны айтады, анықтауы бойынша
матрицасының 0 дәрежесі A реті сияқты жалғыз матрицаны айтады, анықтауы бойынша
![]()
Диагональ және квазидиогональ матрицалардың дәрежелері мына формулалармен есептелінеді:
![]()
![]()
![]()
![]()
![]() – ерекше емес матрица болсын, онда көбейтуді қанағаттандыратын жалғыз матрица болады
– ерекше емес матрица болсын, онда көбейтуді қанағаттандыратын жалғыз матрица болады
![]()
Бұл матрица ![]() матрицасына кері матрица деп аталады және ол
матрицасына кері матрица деп аталады және ол ![]() деп жазылады, сондықтан
деп жазылады, сондықтан
![]()
![]() матрицасының элементтерін
матрицасының элементтерін ![]() арқылы белгілейміз және көрсетеміз, олар
арқылы белгілейміз және көрсетеміз, олар ![]() матрицасының
матрицасының ![]() элементтерінің жалғыз түрімен көрсетіледі
элементтерінің жалғыз түрімен көрсетіледі
![]()
Мұнда ![]()
![]() тіркеп, n теңдеуінің
тіркеп, n теңдеуінің ![]() n белгісізбен бірге біртекті емес сызықты жүйені аламыз,
n белгісізбен бірге біртекті емес сызықты жүйені аламыз, ![]() матрицасының
матрицасының ![]() бағанының элементтері болып табылатын. Бұл жүйенің анықтауышы
бағанының элементтері болып табылатын. Бұл жүйенің анықтауышы ![]() -ға тең бола, 0-ден өзгеше, өйткені
-ға тең бола, 0-ден өзгеше, өйткені ![]() матрицасы өзгеше емес. Көрсетілген жүйенің жалғыз шешімі болады, оны белгілі Крамер ережесімен табуға болады. Мынаны аламыз
матрицасы өзгеше емес. Көрсетілген жүйенің жалғыз шешімі болады, оны белгілі Крамер ережесімен табуға болады. Мынаны аламыз
![]()
Мұндағы ![]() -
- ![]() анықтауышында
анықтауышында ![]() элементінің алгебралық толықтауышы.
элементінің алгебралық толықтауышы.
Байқайық, ![]() матрицасы да теңдеудің шешімі болады
матрицасы да теңдеудің шешімі болады
![]() ,
,
сондықтан
![]()
![]() кері матрицаны қолданып, біз өзгерісті мына түрде жаза аламыз
кері матрицаны қолданып, біз өзгерісті мына түрде жаза аламыз
![]() .
.
Бұл үшін (1) теңдікті ескере отырып, ![]() теңдігінің екі жағында сол жағынан
теңдігінің екі жағында сол жағынан ![]() -ге көбейтеміз.
-ге көбейтеміз.
Белгілі,
![]() .
.
Сенуге қиын емес, диагональды және квазидиагональды матрицалар үшін кері матрицалар мына формулаларда тұрады:
![]()
![]()
![]()
![]()
Егер ![]() – ерекше емес матрицалар, онда *
– ерекше емес матрицалар, онда *
![]()
яғни матрица, ![]() матрицасының туындысына қарама-қарсы, кері тәртіпте алынған, кері матрицаның туындысына тең.
матрицасының туындысына қарама-қарсы, кері тәртіпте алынған, кері матрицаның туындысына тең.
Ерекше емес матрицаның біртұтас теріс дәрежесі мына теңдікпен анықталады
![]()
Диагональды және квазидиагональды матрицалардың біртұтас теріс дәрежесі мына формулалармен есептелінеді:
![]()
![]()
![]()
![]()
Тағы матрицаларды транспонирлеулер операциясын қарастырайық. ![]() -дан алынған матрица ,жол мен бағанның орны ауыстырылған,
-дан алынған матрица ,жол мен бағанның орны ауыстырылған,![]() матрицасына қатысты транспонирленген матрица деп аталады. Оны былай белгілей отырып
матрицасына қатысты транспонирленген матрица деп аталады. Оны былай белгілей отырып ![]() , мынаны аламыз
, мынаны аламыз
![]()
Егер ![]() симметриялы болса, онда
симметриялы болса, онда ![]() .
.
Егер ![]() кососимметриялы болса, онда
кососимметриялы болса, онда ![]() .
.
Транспонирлену операциясы мына заңға бағынатыны айқын
![]()
Матрицаның сандық сипаттамалары. Матрицаның элементарлық бөлгіштері.
Матрица берілсін
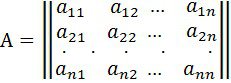 .
.
элементтерінің мәні заттай сандар.
Матрица құрайық
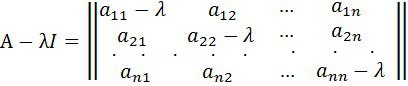 .
.
Бұл матрица, ![]() матрицасы үшін матрицаның сипаттамасы деп аталады. Матрица сипаттамасының анықтауышы
матрицасы үшін матрицаның сипаттамасы деп аталады. Матрица сипаттамасының анықтауышы
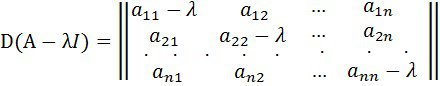
![]() матрицасының сипаттамалық анықтауышы немесе сипаттамалық полиномасы деп аталады, λ-ның n дәрежесінің полиномы болып табылатын. Мына теңдеу
матрицасының сипаттамалық анықтауышы немесе сипаттамалық полиномасы деп аталады, λ-ның n дәрежесінің полиномы болып табылатын. Мына теңдеу
![]()
![]() матрицасының сипаттамалық теңдеуі деп аталады, ал оның түптері
матрицасының сипаттамалық теңдеуі деп аталады, ал оның түптері ![]() -
- ![]() матрицасының сипаттамалық сандары деп аталады.
матрицасының сипаттамалық сандары деп аталады.
![]() матрицасының қарапайым бөлгіштері туралы түсінік берейік.
матрицасының қарапайым бөлгіштері туралы түсінік берейік. ![]() -
- ![]() еселігінің сипаттамалық саны болсын. Онда сипаттамалық анықтауыш
еселігінің сипаттамалық саны болсын. Онда сипаттамалық анықтауыш ![]() ,
, ![]() -не (қалдықсыз) бөлінеді.
-не (қалдықсыз) бөлінеді.
![]() сандарын қарастырайық,
сандарын қарастырайық,
![]()
теңдіктерімен анықталатын.
Осы сандардың барлығы 1-ден кіші емес, ал олардың соммасы ![]() –ға тең, яғни
–ға тең, яғни![]() сипаттамалық санының еселігі.
сипаттамалық санының еселігі.
Өрнек құрастырайық
![]()
Бұл өрнектер, әлбетте,![]() сипаттамалық анықтауыштың бөлгіштері болып табылады. Олар
сипаттамалық анықтауыштың бөлгіштері болып табылады. Олар ![]() матрицасының қарапайым бөлгіштері деп аталады,
матрицасының қарапайым бөлгіштері деп аталады, ![]() сипаттамалық санына тиісті. Ескертейік, барлық қарапайым бөлгіштердің сомма көрсеткіші, көрсетілген сипаттамалық санға сәйкес, оның еселіктері тең.
сипаттамалық санына тиісті. Ескертейік, барлық қарапайым бөлгіштердің сомма көрсеткіші, көрсетілген сипаттамалық санға сәйкес, оның еселіктері тең. ![]() матрицасында қарапайым бөлгіш
матрицасында қарапайым бөлгіш![]() болуы мүмкін. Осындай қарапайым бөлгіш жай деп аталады.
болуы мүмкін. Осындай қарапайым бөлгіш жай деп аталады. ![]() түрінде берілген қарапайым бөлгіш жай емес деп аталады.
түрінде берілген қарапайым бөлгіш жай емес деп аталады.
Егер ![]() матрицасында бірнеше әртүрлі сипаттамалық сандары болса, онда, қарапайым бөлгіштерді салып беріп, олардың әрқайсысына сәйкес,
матрицасында бірнеше әртүрлі сипаттамалық сандары болса, онда, қарапайым бөлгіштерді салып беріп, олардың әрқайсысына сәйкес, ![]() матрицасының барлық қарапайым бөлгіштерінің жиынтығын аламыз, оны мына түрде жазамыз
матрицасының барлық қарапайым бөлгіштерінің жиынтығын аламыз, оны мына түрде жазамыз
![]()
мұндағы ![]() сандарының арасында теңдері де болуы мүмкін, ал
сандарының арасында теңдері де болуы мүмкін, ал ![]() – бүтін сан, әрі олардың соммасы
– бүтін сан, әрі олардың соммасы ![]() матрицасының ретіне тең
матрицасының ретіне тең
![]()
1мысал. Матрицаны қарастырайық
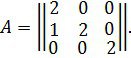
Мұнда
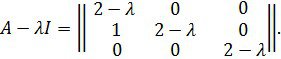
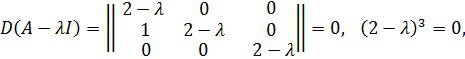
Сондықтан матрица бір үш есе сипаттамалық санға ие ![]() Ортақ ең көп екінші ретті анықтауыштардың бөлгіші λ
Ортақ ең көп екінші ретті анықтауыштардың бөлгіші λ![]()
![]() матрицасының бір элементі, яғни нақты
матрицасының бір элементі, яғни нақты ![]() , λ
, λ![]() -ге бөлінбейді. Сондықтан
-ге бөлінбейді. Сондықтан
![]()
Және ![]() матрицасының қарапайым бөлгіштері
матрицасының қарапайым бөлгіштері
![]()
болады.
Мұнда ![]() матрицасында бір жай емес және бір жай қарапайым бөлгіші бар.
матрицасында бір жай емес және бір жай қарапайым бөлгіші бар.
2мысал. Матрицаның қарапайым бөлгіштерін табу
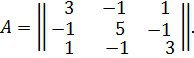
Бізге берілгені
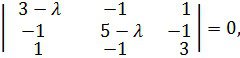
![]()
![]()
![]()
Барлық сипаттамалық сандары жай болғандықтан, онда ![]() матрицасының қарапайым бөлгіштері
матрицасының қарапайым бөлгіштері
![]()
болады.
3мысал. Диагональді матрицаның қарапайым бөлгіштері
![]()
болады
![]()
4мысал. Мына түрдегі квазидиагональді матрицаны қарастырайық
![]()
Бұл жердегі ![]() -де біз
-де біз![]() санды ұйғарамыз,
санды ұйғарамыз, ![]() сандарының арасында теңдері де болуы мүмкін.
сандарының арасында теңдері де болуы мүмкін.
Бұл матрицада ![]() сипаттамалық сандары бар, еселіктері
сипаттамалық сандары бар, еселіктері ![]() .
.
![]() матрицасының қарапайым бөлгіштері
матрицасының қарапайым бөлгіштері
![]()
болады.
2.2 Матрицаларды дифференциалдау және интегралдау.
Матрицаны қарастырайық
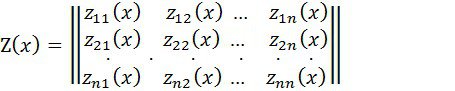
элементтері x-тің функциялары болып табылады.
![]() матрицасының барлық элементтерің
матрицасының барлық элементтерің ![]() нүктесінде туындысы бар деп болжап көрейік. Онда
нүктесінде туындысы бар деп болжап көрейік. Онда ![]() нүктесінде
нүктесінде ![]() матрицасынан туындыны мына теңдік арқылы анықтайық
матрицасынан туындыны мына теңдік арқылы анықтайық
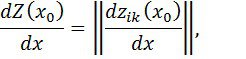
сондықтан матрицаны дифференциалдау, оның барлық элементтерін дифференциалдауға алып келеді.
Функцияны дифференциалдаудың әдеттегі ережелері әділетті және матрицаны дифференциалдауға да.
Егер ![]() – түпкілікті матрица болса, онда
– түпкілікті матрица болса, онда
![]() ,
,
![]()
![]()
![]() ( )
( )
және де ( ) формулада көбейткіштердің орнын ауыстыруға болмайды.
![]() матрицасының бүтін оң дәрежесінің туындысы, соңғы ережені дәйекті қолдану жолымен есептелінеді. Мынаны аламыз
матрицасының бүтін оң дәрежесінің туындысы, соңғы ережені дәйекті қолдану жолымен есептелінеді. Мынаны аламыз
![]()
![]()
Жалғастыра, табамыз
![]()
Бұл әжептәуір қиын формула ықшамдалады, егер ![]() матрицасы туындысымен коммутировать етсе, яғни егер
матрицасы туындысымен коммутировать етсе, яғни егер
![]() ()
()
Бұл жағдайда біз ереже аламыз,әдеттегі ереже тәрізді күрделі дәрежелі функцияны дифференциалдау
![]()
![]() кері матрицадан туындыны есептеу үшін, тепе-теңдікті дифференциалдаймыз
кері матрицадан туындыны есептеу үшін, тепе-теңдікті дифференциалдаймыз
![]()
Мынаны аламыз
![]()
Осыдан
![]()
немесе
![]()
Бұл формуладан көріп тұрғанымыз, ![]() және
және ![]() бар болса,
бар болса, ![]() барлық нүктелерде бар болады. Егер ( ) шарт орындалса, онда
барлық нүктелерде бар болады. Егер ( ) шарт орындалса, онда
![]() ,
,
олай болса
![]()
Матрицаны интегралдау операциясы,кері дифференциалдау операциясы сияқты анықталады
![]()
немесе
![]() .
.
Мынаған сенуге оңай
![]()
![]()
![]() .
.
2.3 Біртекті сызықтық жүйенің матрицалық түрде жазылуы мен шешімі
Біртекті сызықты жүйеге мәндес,матрицалық теңдеу құру
![]() Жүйені қарастырайық
Жүйені қарастырайық
![]() (k
(k![]() ) , (1)
) , (1)
кейбір (a,b) интервалында ![]() коэфициенттері үзіліссіз.
коэфициенттері үзіліссіз.
Мынаған мұқият назар аударайық, осы жерде алдағы есептеулерді оңай шешу үшін, біз бұрындары пайдаланылған жүйелердің жазбаларындағы коэфициенттердің индекстерінің ретін өзгертеміз. Енді ![]() коэфициентінің бірінші индексі,
коэфициентінің бірінші индексі, ![]() ізделінді функциясының номерімен сәйкес келеді, ал екіншісі теңдеудің номерін көрсетеді.
ізделінді функциясының номерімен сәйкес келеді, ал екіншісі теңдеудің номерін көрсетеді.
Мейлі
![]() ,
,![]() , … ,
, … , ![]() (
(![]() ) (2)
) (2)
шешімдердің фундаментальді жүйелері бар. (2) шешімнің әрқайсысын (1) жүйеге ретімен қойып, ![]() тепе-теңдігін аламыз:
тепе-теңдігін аламыз:
![]() (
(![]() ,k
,k![]() ) .
) .
Әрине ![]() тепе-теңдігін бір матрицалық тепе-теңдікке ауыстыруға әрекет жасау керек. Осы мақсатпен талқылауға екі матрица енгіземіз:
тепе-теңдігін бір матрицалық тепе-теңдікке ауыстыруға әрекет жасау керек. Осы мақсатпен талқылауға екі матрица енгіземіз:
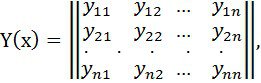
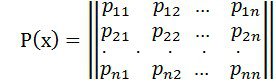 .
.
мұндағы ![]() - (1) жүйенің шешімінің фундаментальді жүйесінің матрицасы, ал
- (1) жүйенің шешімінің фундаментальді жүйесінің матрицасы, ал ![]() – матрица, осы жүйенің транспонерленген матрицасының коэфициенттерімен алынған. Онда анық, мына
– матрица, осы жүйенің транспонерленген матрицасының коэфициенттерімен алынған. Онда анық, мына
![]() ,
,
![]()
(![]() ),
),
олай болса тепе-теңдікті мына түрде көшіріп жазуға болады
![]() (
(![]() )
)
немесе бір матрицалық тепе-теңдік түрінде
![]() (3)
(3)
яғни фундаментальді жүйенің матрицасы (1) жүйенің шешімі мына теңдеудің шешімі болып табылады
![]() (4)
(4)
Бұл теңдеу (1) жүйеге сәйкес матрицалық теңдеу деп аталады.
Ендігәрі ![]() матрицасын, (4) теңдеуді (3) тепе-теңдікке айналдыратын,
матрицасын, (4) теңдеуді (3) тепе-теңдікке айналдыратын, ![]()
интервалында (4) теңдеудің интегралды матрицасы деп атаймыз, егер оның анықтауышы ![]() , осы интервалдан
, осы интервалдан ![]() -тің барлық мағыналарына.
-тің барлық мағыналарына.
Матрица шешімдерінің бастапқы мағынасы, фундаментальді жүйені құрушы,![]() интегралды матрицасына сәйкес бастапқы мағынасы деп аталады.
интегралды матрицасына сәйкес бастапқы мағынасы деп аталады. ![]() интегралды матрицасының бастапқы мағынасын
интегралды матрицасының бастапқы мағынасын ![]() арқылы белгілейміз, сондықтан
арқылы белгілейміз, сондықтан
![]()
![]() . (5)
. (5)
![]() интегралды матрицасының анықтауышы үшін мына формула орындалады
интегралды матрицасының анықтауышы үшін мына формула орындалады
![]() ,
,
мұндағы
![]()
![]() матрицасының ізі бар.
матрицасының ізі бар.
Матрицалық теңдеудің ортақ екі қасиеті, біртекті сызықтық жүйеге қатысты
(4) матрицалық теңдеудің екі ортақ қасиетін белгілейік.
1. (4) теңдеу
![]()
![]() ,
,
мұндағы ![]() – үзіліссіз дифференциалданатын функция, әрі
– үзіліссіз дифференциалданатын функция, әрі ![]() аралығында
аралығында ![]() ,
, ![]() және
және ![]() .
.
Шыныменде, мынаны аламыз
![]() .
.
Сондықтан, (4) теңдеуге ![]() қойып, аламыз
қойып, аламыз
![]()
немесе
![]()
мұндағы
![]() .
.
2.(4) теңдеу сызықты болып қалады, егер ![]() интегралды матрицаның орнына жаңа
интегралды матрицаның орнына жаңа ![]() интегралды матрицаны енгізсек, мына алмастыру арқылы
интегралды матрицаны енгізсек, мына алмастыру арқылы
![]() (8)
(8)
Мұндағы ![]() – ерекше емес дифференциалданған матрица.
– ерекше емес дифференциалданған матрица.
Шыныменде, себебі
![]() ,
,
(4) теңдеуде (8) алмастыруды орындай, мынаны аламыз
![]()
осыдан
![]()
немесе
![]()
мұндағы
![]() .
.
Егер, дербес жағдайда, Q![]()
![]() , онда
, онда
![]()
Сондықтан алмастыру
![]()
![]()
осы теңдікке алып келеді, мұндағы ![]() матрица
матрица ![]() сияқты матрицаға ауысады,
сияқты матрицаға ауысады, ![]() сияқты матрицасымен бірге:
сияқты матрицасымен бірге:
![]() .
.
Интегралды матрицаның негізгі қасиеттері
1. Егер ![]() - (4) теңдеудің интегралды матрицасы болса, онда матрица
- (4) теңдеудің интегралды матрицасы болса, онда матрица
![]() (9)
(9)
Мұндағы ![]() - кез-келген тұрақты ерекше емес матрица, сондай-ақ осы теңдеудің интегралды матрицасы болып табылады.
- кез-келген тұрақты ерекше емес матрица, сондай-ақ осы теңдеудің интегралды матрицасы болып табылады.
Шыныменде, ![]() дифференциалдап, мынаны аламыз
дифференциалдап, мынаны аламыз
![]()
Бірақ ![]() . Сондықтан
. Сондықтан
![]()
немесе
![]() .
.
Сонымен қатар, ![]() ,
, ![]() . Демек,
. Демек, ![]() (4) теңдеудің интегралды матрицасы бар.
(4) теңдеудің интегралды матрицасы бар.
2. Егер ![]() - (4) теңдеудің интегралды матрицасы болса, (a,b) интервалында анықталған, онда барлық интегралды матрицалар, осы интервалда анықталған, (9) формулада бар.
- (4) теңдеудің интегралды матрицасы болса, (a,b) интервалында анықталған, онда барлық интегралды матрицалар, осы интервалда анықталған, (9) формулада бар.
Шыныменде, ![]() - (4) теңдеудің интегралды матрицасы болсын, бастапқы шартты қанағаттандыратын
- (4) теңдеудің интегралды матрицасы болсын, бастапқы шартты қанағаттандыратын
![]() .
.
![]() және
және ![]() (9)-ға қойып, мына теңдеуді аламыз
(9)-ға қойып, мына теңдеуді аламыз
![]() ,
,
осыдан
![]() .
.
Табылған ![]() матрицасының мәнін (9) формулаға қойып, интегралды матрицаны аламыз
матрицасының мәнін (9) формулаға қойып, интегралды матрицаны аламыз
![]() .
.
Бұл интегралды матрица ![]() матрицасы тәрізді бастапқы мағынаға ие болғандықтан, жекешелеп теоремасынан осы екі интегралды матрицалар бір-біріне сәйкес келеді, осыдан біз аламыз
матрицасы тәрізді бастапқы мағынаға ие болғандықтан, жекешелеп теоремасынан осы екі интегралды матрицалар бір-біріне сәйкес келеді, осыдан біз аламыз
![]()
Ақырында, кез-келген интегралды матрица (9) формуладан алынады, ![]() матрицасын лайықты таңдағанда.
матрицасын лайықты таңдағанда.
Егер, дербес жағдайда, ![]() интегралды матрицасы
интегралды матрицасы ![]() нүктесінде нормаланған болса, онда кез-келген
нүктесінде нормаланған болса, онда кез-келген ![]() интегралды матрицасы
интегралды матрицасы ![]() арқылы мына формуламен айқындалады
арқылы мына формуламен айқындалады
![]()
2.4Лаппо – Данилевский жағдайы
Болжап көрейік,![]() матрицасы өзінің интегралымен коммутировать етсе:
матрицасы өзінің интегралымен коммутировать етсе:
![]() (10)
(10)
Бұл жағдайда интегралды матрицаның орнына алуға болады
![]() . (11)
. (11)
Шыныменде, (11) формуланы дифференциалдап, мынаны аламыз
![]() немесе
немесе ![]()
яғни (11) матрица (4) теңдеудің интегралды матрицасы болады.
(11) матрица ![]() нүктесінде нормаланған екенін байқайық.
нүктесінде нормаланған екенін байқайық.
(10) шарт, дербес жағдайда, белгілі, орындалған, егер ![]() , яғни бізде біртекті сызықты жүйе дифференциалдық теңдеулердің тұрақты коэфициенттерімен бар болса. Бұл жағдайда (4) теңдеу мына түрге енеді
, яғни бізде біртекті сызықты жүйе дифференциалдық теңдеулердің тұрақты коэфициенттерімен бар болса. Бұл жағдайда (4) теңдеу мына түрге енеді
![]() (12)
(12)
Ал оның интегралды матрицасы
![]()
немесе ( ![]() деп болжап)
деп болжап)
![]() . (13)
. (13)
(12) теңдеудің барлық интегралдық матрицалары мына формулада бар
![]()
мұндағы ![]() – ерікті тұрақты ерекше емес матрица.
– ерікті тұрақты ерекше емес матрица.
Түйіндес матрицалық теңдеу
Дифференциалдық теңдеудің жүйесі
![]() (14)
(14)
(1) жүйемен түйіндес, матрицалық түрде былай жазыла алады:
![]() (15)
(15)
мұнда
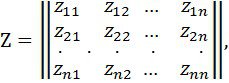
Мұндағы ![]() -
- ![]() матрицасына қатысты транспонерленген матрица.
матрицасына қатысты транспонерленген матрица.
(15) теңдеудің екі бөлігіне де транспонерлеу операциясын жасай отырып, аламыз
![]() (16)
(16)
мұнда
 (17)
(17)
(16) теңдеу (15) теңдеумен түйіндес немесе (15) теңдеуге қосылу деп аталады.
(16) теңдеумен түйіндес (17) интегралды матрицаның бір ерекшелігіне оқушының ерекше назарын аудартайық: ода шешімдері жол бойынша емес,бағандары бойынша қойылған, ![]() интегралды матрицасындағы секілді.
интегралды матрицасындағы секілді.
Сенуге қиын емес, (4) теңдеудің және түйіндес (16) теңдеудің интегралды матрицалары мына арақатынаспен байланысқан
![]() (18)
(18)
Шыныменде, аламыз
![]()
Демек,
![]() . (19)
. (19)
(19) теңдіктен мынау туындайды
![]()
Осыдан, дербес жағдайда, тиісті,егер (4) теңдеудің ![]() интегралды матрицасы болса, онда
интегралды матрицасы болса, онда ![]() түйіндес (16) теңдеудің интегралды матрицасы болады. Осыған байланысты ұмытпау керегі ,
түйіндес (16) теңдеудің интегралды матрицасы болады. Осыған байланысты ұмытпау керегі , ![]() матрицасында шешімдері баған бойынша қойылған.
матрицасында шешімдері баған бойынша қойылған.
Ақырында, (1) жүйені интегралдаудың есебі, түйіндес (14) жүйені интегралдау есебіне тең екеніне тағы да көзіміз жетеді.
Егер (1) жүйе өзі түйіндес болса, яғни ![]() , онда түйіндес (16) теңдеу мына түрге енеді
, онда түйіндес (16) теңдеу мына түрге енеді
![]() (20)
(20)
![]() интегралды матрицасының орнына
интегралды матрицасының орнына ![]() -ті алуға болатыны түсінікті.
-ті алуға болатыны түсінікті.
Шыныменде, егер ![]() (4) теңдеудің интегралды матрицасы болса, онда біз мынандай тепе-теңдік аламыз
(4) теңдеудің интегралды матрицасы болса, онда біз мынандай тепе-теңдік аламыз
![]()
Осы тепе-теңдіктің екі жағын да транспонерлеп, аламыз
![]()
яғни, ![]() (20) теңдеудің интегралды матрицасы.
(20) теңдеудің интегралды матрицасы.
![]() (18) тепе-теңдікке қойып, аламыз
(18) тепе-теңдікке қойып, аламыз
![]()
немесе
![]()
![]()
Осыдан, дербес жағдайда, ![]() болғанда, өзі түйіндес жүйенің әртүрлі шешімдері мына сипатқа ие
болғанда, өзі түйіндес жүйенің әртүрлі шешімдері мына сипатқа ие
![]()
![]() .
.
2.5 Тұрақты коэфициенттері бар біртекті сызықтық жүйені интегралдау
Біртекті сызықтық жүйенің дифференциалдық теңдеулердің тұрақты коэфициенттерімен фундаментальды жүйенің шешімдерінің құрылымы
Жүйені қарастырайық
![]()
![]() , (1)
, (1)
Мұндағы ![]() – заттық сандар. Бұл жүйе матрицалық теңдеуге мәндес
– заттық сандар. Бұл жүйе матрицалық теңдеуге мәндес
![]() (2)
(2)
сонымен бірге
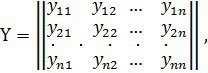
 .
.
(2) теңдеудің интегралды матрицасы
![]() (3)
(3)
болады.
![]() матрицасына байланысты осы интегралды матрицаның құрылымын зерттейік. Соған байланысты біз (1) жүйенің, оның коэфициенттерімен байланысты, фундаментальді жүйенің шешімдерінің құрылымымен танысамыз. Одан әрі көретініміз, бұл құрылым сипаттамалық сандарға
матрицасына байланысты осы интегралды матрицаның құрылымын зерттейік. Соған байланысты біз (1) жүйенің, оның коэфициенттерімен байланысты, фундаментальді жүйенің шешімдерінің құрылымымен танысамыз. Одан әрі көретініміз, бұл құрылым сипаттамалық сандарға![]() және
және ![]() матрицасының қарапайым бөлгіштеріне тәуелді. Оларды білу
матрицасының қарапайым бөлгіштеріне тәуелді. Оларды білу ![]() матрицасын канондық түрге әкелуге көмектеседі.
матрицасын канондық түрге әкелуге көмектеседі.
Алдымен болжайық, ![]() матрицасында жай элементарлық бөлгіштер бар деп
матрицасында жай элементарлық бөлгіштер бар деп ![]() …
… ![]() және, сәйкесінше, ол канондық ұғымға ие
және, сәйкесінше, ол канондық ұғымға ие
![]()
Мұнда![]() сипаттамалық сандардың арасында
сипаттамалық сандардың арасында ![]()
![]() матрицалары бірдей болуы мүмкін.Онда
матрицалары бірдей болуы мүмкін.Онда
![]()
![]() (4)
(4)
(4) интегралды матрицаны сол жағынан ![]() көбейтіп, мынаны аламыз
көбейтіп, мынаны аламыз
![]() .
.
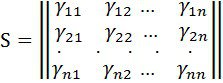 .
.
болсын. Онда
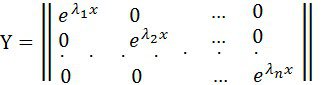 ·
· 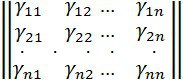
![]()
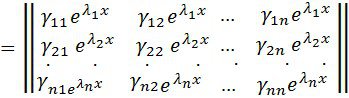 .
.
Енді ортақ жағдайын қарастырайық. ![]() матрицасы элементарлық бөлгіштерге ие болсын
матрицасы элементарлық бөлгіштерге ие болсын
![]()
Мұнда сипаттамалық сандардың арасында ![]() бірдейлері де болуы мүмкін;
бірдейлері де болуы мүмкін; ![]() әрі
әрі ![]() , және, сәйкесінше,
, және, сәйкесінше, ![]() матрицасының канондық түсінігі
матрицасының канондық түсінігі
A![]()
болады. Онда
![]()
![]()
![]()
![]()
немесе
![]() .
.
Осы интегралды матрицаны сол жағынан ![]() көбейтіп, интегралды матрица аламыз
көбейтіп, интегралды матрица аламыз
![]() . (5)
. (5)
![]() матрицасын есептеп шығарайық. Берілгені
матрицасын есептеп шығарайық. Берілгені
![]() (6)
(6)
Одан әрі
![]()
(Мұндағы ![]() –
–![]() ретті бірлік матрица).
ретті бірлік матрица).
Бірақ
![]()
мұндағы

және ![]() болғанда мынаны аламыз
болғанда мынаны аламыз
![]() ,
,
мұндағы

Жалпы алғанда
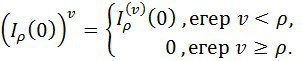
Осыдан шығады,
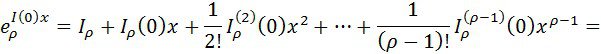
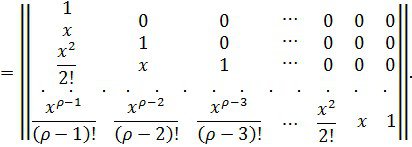
Енді, (6) ескере отырып, аламыз
![]()
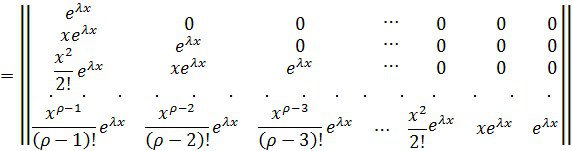
Біртекті сызықты жүйені тұрақты коэфициенттерімен канондық түрге әкелу
Алмастыру берілсін
![]() (
(![]() ) (8)
) (8)
ол (2) теңдеуді мына түрге алып келеді
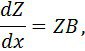
мұндағы ![]() .
. ![]() матрицасын,
матрицасын, ![]() -ның канондық түрі болатындай таңдап аламыз
-ның канондық түрі болатындай таңдап аламыз ![]()
сондықтан
![]()
Онда (8) алмастыру (2) теңдеуді мына түрге алып келеді ![]() (9)
(9)
Алынған (9) теңдеу (2) теңдеуге лайықты, канондық түрдің теңдеуі деп аталады. (9) теңдеудің интегралды матрицасы үшін алуға болады![]()
![]()
немесе
![]()
Бұл ![]() мағынасын (8) формулаға қойып, (2) теңдеудің интегралды матрицасын аламыз немесе (1) жүйенің шешімінің фундаментальді жүйесінің түрі тәрізді
мағынасын (8) формулаға қойып, (2) теңдеудің интегралды матрицасын аламыз немесе (1) жүйенің шешімінің фундаментальді жүйесінің түрі тәрізді
![]()
яғни тағы да (5) түрде.
Дифференциалдық теңдеулердің жүйесі, (9) матрицалық теңдеуге лайықты, (1) жүйенің канондық түрі деп аталады.
(9) матрицалық теңдеуден оған сәйкес дифференциалдық теңдеулер жүйесіне көшейік. Ол үшін еске түсірейік, біз жүйеден матрицалық теңдеуге өткенде, матрицаны жүйенің коэфициенттерімен транспонерлегенбіз. Сондықтан (9) матрицалық теңдеуден сәйкес жүйеге өткенде біз, ![]() матрицасын транспонерлеуіміз керек. Егер тағы осы матрицаның құрылымына назар аударсақ, сенуге қиын емес, біз n теңдеуінің біртекті сызықты жүйесін аламыз, және де ол s группаға бөлінеді, яғни
матрицасын транспонерлеуіміз керек. Егер тағы осы матрицаның құрылымына назар аударсақ, сенуге қиын емес, біз n теңдеуінің біртекті сызықты жүйесін аламыз, және де ол s группаға бөлінеді, яғни ![]() матрицасында әртүрлі қанша қарапайым бөлгіштер болса, сонша топ болады. Әр топта орналасқан теңдеулердің сандары, осы топқа сәйкес, қарапайым бөлгіштердің дәрежесіне тең. Әр топта теңдеулердің диагональді коэфициенттері, сәйкес сипаттамалық сандарына тең, үстіңгі диагоналға қатарлас тұрған коэфициенттер бірге тең, ал қалған коэфициенттер нөлге тең.
матрицасында әртүрлі қанша қарапайым бөлгіштер болса, сонша топ болады. Әр топта орналасқан теңдеулердің сандары, осы топқа сәйкес, қарапайым бөлгіштердің дәрежесіне тең. Әр топта теңдеулердің диагональді коэфициенттері, сәйкес сипаттамалық сандарына тең, үстіңгі диагоналға қатарлас тұрған коэфициенттер бірге тең, ал қалған коэфициенттер нөлге тең.
Сонымен, (1) жүйенің канондық түрі былай болады:
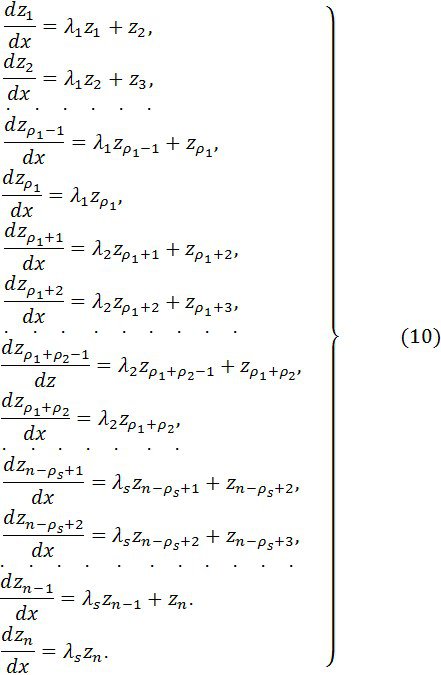
Егер,дербес жағдайда, (1) жүйенің барлық сипаттамалық сандары әртүрлі немесе араларында еселік бар болса, бірақ барлық қарапайым бөлгіштер жай, соған сәйкес (9) канондық матрицалық теңдеу мына түрге келеді
![]()
сәйкесінше, (1) жүйе таза диагональді канондық түрге өзгертілуі мүмкін.
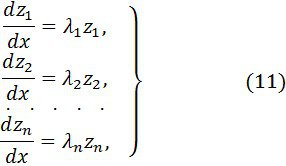
![]() сандарының арасында бірдейлері де болуы мүмкін.
сандарының арасында бірдейлері де болуы мүмкін.
Ақырында, біз (1) әртүрлі біртекті сызықты жүйені (10) немесе (11) канондық түрге әкелуге болатынын дәлелдедік, яғни таза диагональдық түрге немесе квазидиагональдық түрге, матрицаның барлық қарапайым бөлгіштері жай немесе олардың арасында еселік болуына байланысты.
1 мысал. Канондық түрге келтіріп, жүйенің ортақ шешімін табу керек
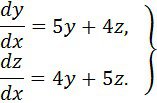
![]() деп алып, жүйені мына түрде көшіріп жазайық
деп алып, жүйені мына түрде көшіріп жазайық
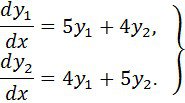
Мұнда
![]()
Сәйкесінше, (14) жүйе, онда берілген (13) жүйе де таза диагональды канондық түрге әкелінеді
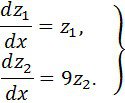
(14) жүйенің фундаментальді жүйесінің шешімі
![]()
болады.
![]() -ті табайық. Берілгені
-ті табайық. Берілгені
![]()
![]()
![]()
болсын, онда
![]()
![]()
![]()
![]()
![]()
![]() деп алып,
деп алып, ![]()
![]() табайық, олай болса
табайық, олай болса
![]()
Табылған ![]() мағынасын (15) формулаға қойып, аламыз
мағынасын (15) формулаға қойып, аламыз
![]()
(13) жүйенің ортақ шешімі
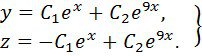
болады.
2 мысал. Мына жүйені қарастырайық
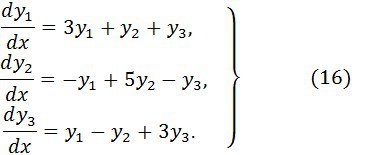
![]() мінездемелік сандары болады. Сондықтан (16) жүйе таза диагональды канондық түрге алып келінеді.
мінездемелік сандары болады. Сондықтан (16) жүйе таза диагональды канондық түрге алып келінеді.
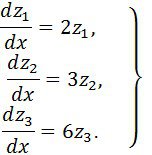
(16) жүйенің фундаментальді жүйесінің шешімі
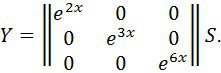
болады.
3 мысал. Берілген жүйе :
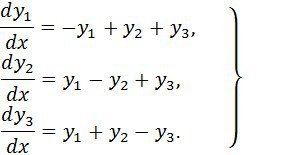
Бұл жүйеде бір жай мінездемелік сан бар ![]() және бір екі мәрте мінездемелік сандары
және бір екі мәрте мінездемелік сандары ![]() бар. Бірақ қарапайым бөлгіштері, еселік түбіріне сәйкес, жай: λ
бар. Бірақ қарапайым бөлгіштері, еселік түбіріне сәйкес, жай: λ![]() , λ
, λ![]() . Сондықтан (17) жүйе таза диагональды канондық түрге әкелінеді
. Сондықтан (17) жүйе таза диагональды канондық түрге әкелінеді
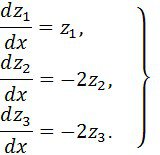
Фундаментальді жүйенің шешімі мына түрде болады
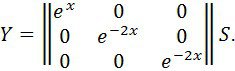
4 мысал. Мынажүйені қарастырайық
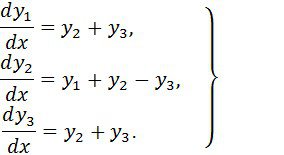
Мұнда бір жай мінездемелік сан:![]() ал басқа еселік:
ал басқа еселік: ![]() Бірақ қарапайым бөлгіш, еселік түбіріне сәйкес, жай емес:
Бірақ қарапайым бөлгіш, еселік түбіріне сәйкес, жай емес: ![]() . Сондықтан (18) жүйе таза емес диагональды түрге әкелінеді, ал квазидиагональдіге:
. Сондықтан (18) жүйе таза емес диагональды түрге әкелінеді, ал квазидиагональдіге:
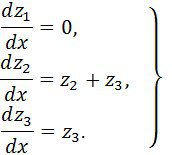
Фундаментальді жүйенің шешімі
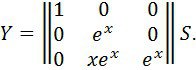
болады.
5 мысал. Жүйені қарастырайық
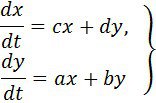
Канондық түрге алып келейік, яғни үш жүйенің біреуіне
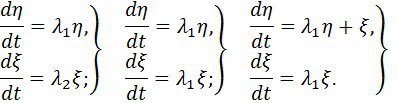
Сондықтан теңдеу үш қарапайым түрдің біреуіне әкелінеді
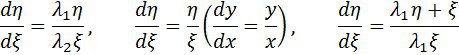
Келтіру жүйелері туралы түсінік
Біртекті сызықтық жүйе берілсін
![]()
![]()
мұндағы ![]() коэфициенттері –
коэфициенттері – ![]() интервалында үзіліссіз шектеулі функциялар. Осы жүйені матрицалық түрде жазайық
интервалында үзіліссіз шектеулі функциялар. Осы жүйені матрицалық түрде жазайық ![]()
Z матрицасын Ляпунов түрінің матрицасы деп атайық, егер ол ![]() және
және ![]() бірге шектеулі болса.
бірге шектеулі болса.
(28) жүйе келтірілген деп аталады, егер Ляпунов түрінің Z сияқты матрицасы болса, онда алмастыру
![]()
(29) теңдеуді мына теңдеуге алып келеді
![]()
мұндағы ![]() – тұрақты матрица.
– тұрақты матрица.
Басқа сөзбен айтқанда, (28) жүйе келтірілген деп аталады, егер мынандай сызықты өзгерту болса
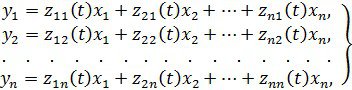
мұндағы ![]() өзгертулерінің коэфициенттерінің мәні шектеулі функциялар, олардың туындылары мен кері өзгертулердің анықтауышымен бірге, жаңа танымал емес функциялар
өзгертулерінің коэфициенттерінің мәні шектеулі функциялар, олардың туындылары мен кері өзгертулердің анықтауышымен бірге, жаңа танымал емес функциялар ![]() мына жүйені қанағаттандырады
мына жүйені қанағаттандырады
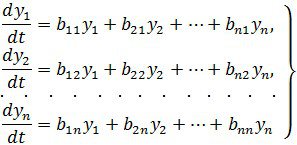
![]() тұрақты коэфициенттерімен.
тұрақты коэфициенттерімен.
Т е о р е м а.
![]()
жүйесі
![]()
жүйесіне келтірілген болу үшін, ![]() тұрақты матрицасымен, қажет және жеткілікті, (30) жүйенің интегралды матрицасы мына құрылымды алса болды
тұрақты матрицасымен, қажет және жеткілікті, (30) жүйенің интегралды матрицасы мына құрылымды алса болды
![]()
мұндағы ![]() – тұрақты матрица, ал Z – Ляпунов түрінің матрицасы.
– тұрақты матрица, ал Z – Ляпунов түрінің матрицасы.
2.6 Сызықтық жүйелерді матрицалық-векторлық тәсілмен интегралдау
Сызықтық жүйенің матрицалық-векторлық шешімі
Сызықтық жүйе берілсін
![]() (k
(k![]() ) , (1)
) , (1)
![]() матрицасының қарастыруына (1) жүйенің коэфициенттерін кіргіземіз және екі вектор-функциялардың – вектор-бағандардың
матрицасының қарастыруына (1) жүйенің коэфициенттерін кіргіземіз және екі вектор-функциялардың – вектор-бағандардың
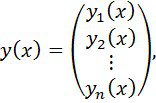
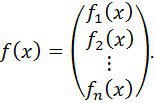
Онда, ![]() теңдігімен туындыны анықтап
теңдігімен туындыны анықтап
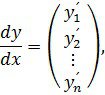
(1)жүйені келесі матрицалық-векторлық түрде жазуға болады
![]() (2)
(2)
Бұл ретте біртекті жүйе
![]() (k
(k![]() ) (3)
) (3)
былай жазылады:![]() (3)
(3)
(a,b) интервалында (2) теңдеудің шешімі вектор-функция – вектор-баған –
![]() деп аталады, айналдыратын (2) теңдеу тепе-теңдікте
деп аталады, айналдыратын (2) теңдеу тепе-теңдікте
![]()
![]() .
.
Дербес жағдайда, ![]()
![]() (a,b) аралығында (3) біртекті теңдеудің шешімі, егер
(a,b) аралығында (3) біртекті теңдеудің шешімі, егер
![]()
![]() . (4)
. (4)
Болжап көрейік, ![]() және
және ![]() (a,b) аралығында үзіліссіз, сонда, Пикарь теоремасы бойынша, (2) теңдеуінің жалғыз ғана шешімі болады
(a,b) аралығында үзіліссіз, сонда, Пикарь теоремасы бойынша, (2) теңдеуінің жалғыз ғана шешімі болады ![]() , бастапқы шартты қанағаттандыратын
, бастапқы шартты қанағаттандыратын
![]() (5)
(5)
мұндағы
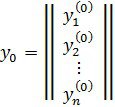
Бастапқы вектор бар, сонымен бірге
![]() (k
(k![]() ).
).
Сонымен қатар бастапқы вектор ![]() өз бетімен беруге болады, және
өз бетімен беруге болады, және![]() шешімін (2) Коши есебімен, (5) көрініп тұрғандай барлық
шешімін (2) Коши есебімен, (5) көрініп тұрғандай барлық ![]() анықталған.
анықталған.
Дербес жағдайда, (3) біртекті теңдеудің жалғыз шешімі, нөлдік бастапқы шартты қанағаттандыратын
![]() ,
,
нөлдік вектор-баған болады
![]() .
.
Матрицалық-векторлық теңдеудің екі ортақ қасиеті, сызықтық жүйеге байланысты
1. (2) теңдеу тәуелсіз айнымалының кез-келген алмастыруында сызықты болып қалады
![]()
![]() (6)
(6)
мұндағы ![]() – (α, β) аралығында үзіліссіз дифференциалданған, әрі
– (α, β) аралығында үзіліссіз дифференциалданған, әрі ![]()
![]() және
және ![]()
![]() болғанда.
болғанда.
Шыныменде, себебі
![]()
(6)-шы алмастыру (2) теңдеуді мына түрге алып келеді
![]()
яғни біз тағы сызықтық теңдеу аламыз.
Атап өтейік, (6) алмастыру (3) теңдеудің сызықтығын да, біртектілігін де бұзбайды.
2. (2) теңдеу ізделінетін вектор-функциялардың кез-келген ерекше емес сызықтық өзгерістерінде сызықты болып қалады.
![]()
мұндағы ![]() –жаңа ізделетін вектор-функция, ал
–жаңа ізделетін вектор-функция, ал ![]() (a, b) аралығында үзіліссіз дифференциалданған, (a, b) аралығында
(a, b) аралығында үзіліссіз дифференциалданған, (a, b) аралығында ![]() матрицасымен.
матрицасымен.
Шыныменде, мынаны аламыз
![]()
![]()
яғни
![]()
мұндағы
![]()
Байқайтынымыз, (3) біртекті теңдеу біртекті болып қалады.
2.7Біртекті матрицалық-векторлық теңдеуді шешудің негізгі қасиеттері
(3) Біртекті теңдеуді қарастырайық
![]()
Жауабы екі тамаша қасиетке ие екенін көрсетейік.
1.Егер ![]() – (3) теңдеудің жауабы болса, онда
– (3) теңдеудің жауабы болса, онда ![]() -та (3) теңдеудің жауабы болады. Мұндағы
-та (3) теңдеудің жауабы болады. Мұндағы ![]() – ерікті тұрақты.
– ерікті тұрақты.
Шыныменде, біз аламыз
![]()
яғни
![]()
Ал бұл, ![]() – (3) теңдеудің шешімі екенін білдіреді.
– (3) теңдеудің шешімі екенін білдіреді.
2.Егер ![]() – (3)теңдеудің шешімі болса, онда олардың сызықты комбинациясы кез-келген тұрақты
– (3)теңдеудің шешімі болса, онда олардың сызықты комбинациясы кез-келген тұрақты ![]() коэфициенттерімен, яғни
коэфициенттерімен, яғни
![]() (7)
(7)
Бұлда (3) теңдеудің шешімі болады.
Шыныменде,
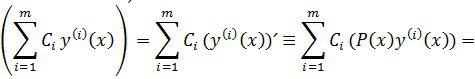
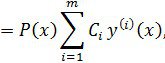
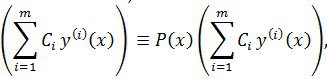
Бұл (7) де ,(3) теңдеудің шешімі болады дегенді білдіреді.
Біртекті матрицалық-векторлық теңдеулердің сызықты тәуелсіз шешімдері және ортақ шешімін құру
![]() (8)
(8)
Шешімі (a, b) интервалында сызықты тәуелсіз деп аталады, егер тепе-теңдік
![]()
(a, b) аралығында тек белгілі жағдайда ғана орындалса, яғни барлық ![]()
(![]() . Кері жағдайда (8) шешім (a, b) аралығында сызықты тәуелді деп аталады.
. Кері жағдайда (8) шешім (a, b) аралығында сызықты тәуелді деп аталады.
Егер n шешіміболса, ![]() ,онда олар (a, b) аралығында сызықты тәуелсіз болады, осы жағдайда ғана, анықтауышы Вронский болғанда
,онда олар (a, b) аралығында сызықты тәуелсіз болады, осы жағдайда ғана, анықтауышы Вронский болғанда
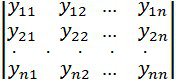
(a, b) аралығында нөлден бөлек. Мұнда шешімдері бағандары бойынша қойылған.
(3)теңдеудің n сызықты тәуелсіз шешімдерінің құрамы осы теңдеудің шешімдерінің фундаментальді жүйесі деп аталады немесе (3) біртекті жүйе тәрізді.
Егер векторлар
![]()
(a, b) аралығында шешімдердің фундаментальді жүйесін құрайды, онда олардың сызықтық комбинациясы ерікті тұрақты коэфициенттерімен,
![]()
(3) теңдеудің ортақ шешімі болып табылады, немесе (3) біртекті сызықтық жүйе тәрізді, мына облыста
![]()
![]() (k
(k![]() ).
).
Оқушыны мынаған назар аудартайық, мұнда ортақ шешімді құру үшін фундаментальді жүйенің шешімімен
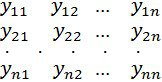
сызықты комбинациялары баған бойынша емес, жол бойынша алынады.
Есептерді шешу мысалдары
1Мысал.
ҚОРЫТЫНДЫ
Бұл дипломдық жұмыста жоғары математика курсында оқытылатын сызықтық дифференциалдық теңдеулердің жүйесі және оларды шешудің тәсілдері, сонымен қатар біртекті сызықтық жүйелерді шешудің матрицалық-векторлық әдіс–тәсілдері, жолдары зерттелді. Атап айтсақ, 1 тарауда біртекті сызықтық дифференциалдық теңдеулер жүйесі және оның қасиеттері,Остроградский – Лиувилль– Якоби формуласы,Фундаментальді жүйенің шешімі бар туралы теорема, 2 тарауда матрица теориясынан кейбір мәліметтер,матрицаның сандық сипаттамалары. Матрицаның элементарлық бөлгіштері, матрицаларды дифференциалдау және интегралдау,біртекті сызықтық жүйенің матрицалық түрде жазылуы мен шешімі, интегралды матрицаның негізгі қасиеттері,түйіндес матрицалық теңдеу,тұрақты коэфициенттері бар біртекті сызықтық жүйені интегралдау,сызықтық жүйелерді матрицалық-векторлық тәсілмен интегралдау, сызықтық жүйенің матрицалық-векторлық түрде жазылуы мен шешімі, матрицалық-векторлық теңдеудің екі ортақ қасиеті, сызықтық жүйеге байланысты қарастырылды.
Есеп шығару — ерекше жұмыс, дәлірек айтсақ ой жұмысы. Ал кез келген жұмысты дұрыс атқару үшін, оның неден тұратыны және оны орындау үшін қандай құрал, әдіс керек екендігін алдын- ала анықтап алу қажет. Кез келген есеп шарттардан және талаптардан құралады.
Есеп шығаруға төмендегідей талаптар қойылады:
Математикалық есептердің танымдық маңызы өте зор. Себебі есеп шығару барысында оқушылардың дүниеге ғылыми көзқарасын қалыптастыруға кең жол ашылады. Бұл мақсатта математиканың диалектикалық табиғатын көрсететін есептерге көбірек көңіл бөлген жөн. Ондай есептер алгебра және анализ бастамаларында, олардың геометриядағы, физикадағы, химиядағы қолданымдарында, сондай-ақ физикалық, механикалық процестердің математикалық модельдерін жасауда жиі кездеседі.
Теңдеуді шешу дегеніміз оның барлық түбірлерін табу немесе оның түбірлері жоқ екенін дәледеу.
Қорыта келгенде, өз пікірім бойынша жоғарғы математика курсында оқытылатын сызықтық диффференциалдық теңдеулерді шешуге арналған бұл жұмыс тереңдетіп оқытылатын жоғарғы сынып оқушыларына және колдледж студенттеріне көмекші құрал орнына қолдануға болады.
Қолданылған әдебиеттер тізімі
1 Мәукеев Б.И. Дифференциалдық теңдеулерді шешу. А.: Мектеп,1989. – 232б.
2 Мәукеев Б.И. Дифференциалдық теңдеулерді шешу әдістері / Б Мәукеев. – Алматы : Мектеп,1989. – 50 б.
3 Кадикенов Б.М. Дифференциалдық теңдеулердің есептері мен жаттығулары. Алматы. “Қазақ университеті”. 2002.
4 Мырзалыұлы Ж. Дифференциалдық теңдеулер. Алматы. “Қазақ университеті”. 2006.
5 Сүлейменов Ж.С. Дифференциалдық теңдеулер. Алматы, Б.1. «Рауан», 1991 жыл.
6 Сүлейменов Ж.С. Дифференциалдық теңдеулер. Алматы, Б.2. «Рауан», 1996 жыл.
7 Тілеубердиев Б. Дифференциалдық теңдеулер. Шымкент. 2004
8 Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. Минск, “Выш. школа”, 1974.
9 Матвеев Н.М. Дифференциальные уравнения. М.1988
10 Петровский И.Г. Лекции по теории дифференциальных уравнений. М., “Наука”. 1984.
11 Самойленко А.М. и другие. Дифференциальные уравнения. М. Высшая школа.1989.
12 Эльсгольц Л.Е. Дифференциальные уравнения и вариационное исчисление. М.Наука. 1965.
13 Г.М.Фихтенгольц «Математикалық анализ негіздері»
14 Байбазаров М.Б. Дифференциалдық және интегралдық есептеулер: Жоғары оқу орындары студенттеріне арналған оқу құралы / М.Б. Байбазаров, Ө.Д.Ершібаев. -. Алматы
15 Г.М. Фихтенгольц «Дифференциялдық және интегралдық есептеулер курсы»
16 Петровский И.Г. Лекций по теорий дифференциальных уравнений. М., «Наука» , 1984 год.
17 Потрягин Л.С. Обыкновенные дифференциальные уравнения. М., «Наука», 1976 год.
18 СтепановВ.В Курс дифференциальных уравнений. М., Физматгиз, 1985 г.
19 Тихонов А.Н. Василева А.В., Свешников А.Г. Дифференциальные уравнения. М., «Наука», 1980 год.
20 Филипов А.Ф. Сборник задач по Дифференциальные уравнения. М., «Наука», 1976 год.
21 В.П. Минорский «Сборник задач по высшей математике».М «Наука»1987
22 Карташев А.П. Рождественский Б.Л. Обыкновенные дифференциальные уравнения и основы вариацианного исчисления. М., « Наука », 1976 год.
23 Шалбаев Е., Сатығұлова С. Дифференциалдық теңдеулер курсынан әдістемелік құрал және бақылау жұмысының мәтіндері. Алматы 2000
24 Еругин Николай павлович. Метод Лаппо данилевского в теории линейных дифференциальных уравнений. Ленинград 1956.
25 Лаппо-Данилевский И.А. Применение функций от матриц к теории линейных систем обыкновенных дифференциальных уравнений. М.: ГИТТЛ, 1957
26 Лаппо-Данилевский И.А. Теория функций от матриц и системы линейных дифференциальных уравнений. Л.-М., ГИТТЛ, 1934
27 Наймарк М.А. Линейные дифференциальные операторы (2-е изд.). М.: Наука, 1969
28 Паламодов В.П. Линейные дифференциальные операторы с постоянными коэффициентами. М.: Наука, 1967
29 Адамар Ж. Задача Коши для линейных уравнений с частными производными гиперболического типа. М.: Наука, 1978
30 Бергман С. Интегральные операторы в теории линейных уравнений с частными производными. М.: Мир, 1964
31 Горбузов В.Н. Интегралы дифференциальных систем. Гродно: ГрГУ, 2006
32 Егоров Д. Интегрирование дифференциальных уравнений (3-е изд.). М.: Печатня Яковлева, 1913
33 Камке Э. Справочник по дифференциальным уравнениям в частных производных первого порядка. М.: Наука, 1966
34 Ладыженская О.А., Солонников В.А., Уралыдева Н.Н. Линейные и квазилинейные уравнения параболического типа. М.: Наука, 1967
35 Ладыженская О.А., Уральцева Н.Н. Линейные и квазилинейные уравнения эллиптического типа (2-е изд.). М.: Наука, 1973
36 Михайлов В.П. Дифференциальные уравнения в частных производных.М.: Наука, 1976
37 Назимов П.С. Об интегрировании дифференциальных уравнений. М.: МГУ, 1880
38 В. Данко «Высшая математика в задачах и упражнениях»
39 Берман Г.Н. Сборник задач по курсу математического анализа М. Наука 1969
40 Дифференциальные уравнения. Темат. Сб.Науч.Тр. Профессор-преподават. Состава и аспирантов вузов М-ва просвещения КазССР/Каз.пед. ин-т им.Абая,Редкол.. Гольцер Я.М – Алма-Ата. КазПИ,1981.
41 Дифференциальные уравнения и их приложения. Темат. Сборник научных тружов. Алма-Ата. КазПИ им.Абая,1984.
42 Дифференциальные уравнения и задачи прикладного Анализа. – Алма-Ата. КазГУ,1982.
43 Көбесов А. Математика тарихы.-А.1998
44 Қазақша-орысша орысша-қазақша терминологиялық сөздік. Казахско-русский русско-казахский терминологический словарь. – Алматы: Рауан, 1999. – 248
45 Қазақша-орысша орысша-қазақша терминологиялық сөздік. – Алматы: Рауан. – 1999 Т.2: Математика. - 248б.
0 комментариев