Санкт-Петербургский политехнический университет
петра великого
Институт металлургии, машиностроения и транспорта
Отделение технологий машиностроения
Кафедра «Мехатроника и роботостроение» (при ЦНИИ РТК)
Лабораторная работа №1
«Построение системы нечеткого вывода»
по дисциплине «Математические методы искусственного интеллекта»
Выполнила студентка группы 13345/2 _________________С. С. Орлова
Работу принял ______________ Л.А. Станкевич
Задачи работы
Создать систему нечеткого вывода для вычисления требуемой зависимости. Работа должна содержать следующие этапы:
1. Аналитический расчет заданной зависимости.
2. Аппроксимация полученного выражения с использованием пяти термов для каждой физической величины.
3. Сравнение результатов аппроксимации с теоретическими значениями в 10 точках. Вычисление средней ошибки.
Выполнение работы
1. Аналитический расчет заданной зависимости
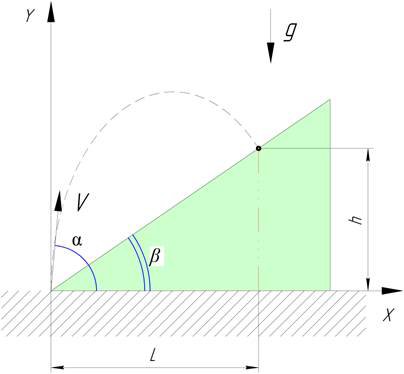
Имеется задача стрельбы в заданную точку на поверхности горы (рисунок 1).
|
Дано: Начальная скорость стрельбы: V = const = 1000 м/с. Ускорение свободного падения: g = 9.81 м/с2. Найти: Зависимость α = f(L, β), где L - расстояние до целевой точки по оси Х; α - угол стрельбы, β - угол наклона горы; (h - расстояние до целевой точки по оси Y, h = L * tg(β) (*)) |
Рис. 1. Стрельба в заданную точку на поверхности горы |
При аналитическом методе решения этой задачи воспользуемся уравнением траектории для тела, брошенного под углом к горизонту:
|
|
(1) |
у - координата по оси Y, х - координата по оси Х.
Из уравнения (1) можно получить искомую зависимость, подставив координаты целевой точки:
· x = L,
· y = h = L * tg(β) из соотношения (*).
Поскольку в процессе вычисления α приходится дважды извлекать квадратный корень и использовать arccos(), получается пять вариантов решения. Условию α ![]() [0, π] удовлетворяют два варианта, выражения и графики для них представлены ниже:
[0, π] удовлетворяют два варианта, выражения и графики для них представлены ниже:
![]() (2а)
(2а)
![]() (2б)
(2б)
|
|
|
|
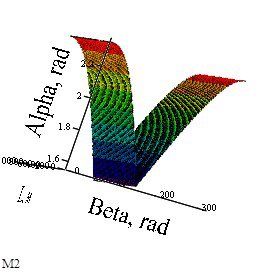
Рис. 2a. График α = f(L, β) = a1(b, L) |
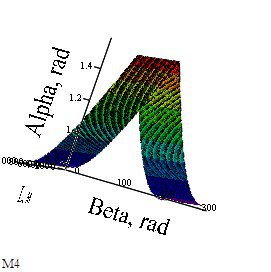
Рис. 2б. График α = f(L, β) = a2(b, L) |
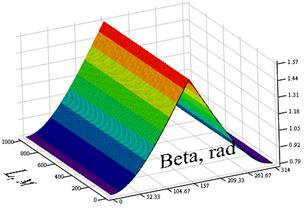
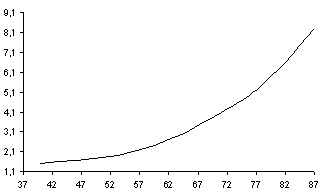
Возьмем зависимость (2б): α = f(β, L) = a2(b, L), рисунок 2б. Выражение будем использовать для вычисления набора точек, служащих входом нечеткой системы, а график будем сравнивать с графиком нечеткой системы, оценивая правильность решения визуально и по 10 точкам.
2. Построение нечеткой системы
2.1 Задание функций принадлежности термов входных и выходных величин
Функции принадлежности термов входных и выходных величин задаются в программе fuzzy logic, все заданные параметры приведены в таблице 1. В данной работе использовано два варианта задания термов - с равномерным распределением и с неравномерным распределением, учитывающим особенности заданной зависимости.
Таблица 1. Функции принадлежности термов с равномерным распределением
|
Переменная |
Физический смысл |
Расстояние L до точки по оси Х |
Угол β горы |
Угол α стрельбы |
|
Тип |
вход |
вход |
выход |
|
|
Название |
L |
Beta |
Alpha |
|
|
Диапазон значений |
[0 1000] м |
[0 π] рад |
[0.75 1.6] рад |
|
|
ФП 1 |
Имя ФП |
Lxs |
Bxs |
Axs |
|
Тип ФП |
gaussmf |
gaussmf |
gaussmf |
|
|
Параметры |
[110 0] |
[0.35 0] |
[0.1 0.75] |
|
|
ФП 2 |
Имя ФП |
Ls |
Bs |
As |
|
Тип ФП |
gaussmf |
gaussmf |
gaussmf |
|
|
Параметры |
[110 250] |
[0.35 0.7854] |
[0.1 0.9625] |
|
|
ФП 3 |
Имя ФП |
Lm |
Bm |
Am |
|
Тип ФП |
gaussmf |
gaussmf |
gaussmf |
|
|
Параметры |
[110 500] |
[0.35 1.571] |
[0.1 1.175] |
|
|
ФП 4 |
Имя ФП |
Ll |
Bl |
Al |
|
Тип ФП |
gaussmf |
gaussmf |
gaussmf |
|
|
Параметры |
[110 750] |
[0.35 2.356] |
[0.1 1.388] |
|
|
ФП 5 |
Имя ФП |
Lxl |
Bxl |
Axl |
|
Тип ФП |
gaussmf |
gaussmf |
gaussmf |
|
|
Параметры |
[110 1000] |
[0.35 3.142] |
[0.1 1.6] |
Таблица 2. Функции принадлежности термов с неравномерным распределением
|
Имя ФП |
Lxs |
Ls |
Lm |
Ll |
Lxl |
|
Параметры |
[150 0] |
[110 300] |
[150 550] |
[150 750] |
[150 1000] |
|
Имя ФП |
Bxs |
Bs |
Bm |
Bl |
Bxl |
|
Параметры |
[0.5 0] |
[0.3 0.95] |
[0.15 1.51] |
[0.35 2.1] |
[0.5 3.142] |
|
Имя ФП |
Axs |
As |
Am |
Al |
Axl |
|
Параметры |
[0.11 0.75] |
[0.1 1] |
[0.08 1.2] |
[0.1 1.39] |
[0.08 1.6] |
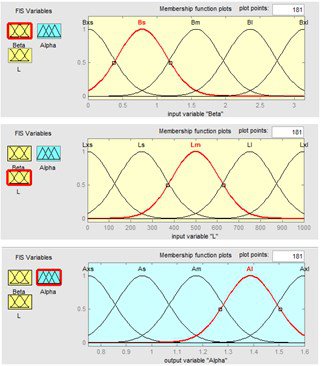
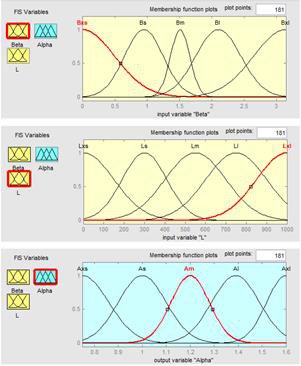
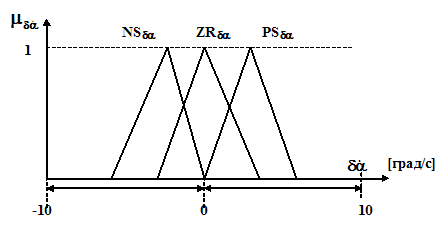
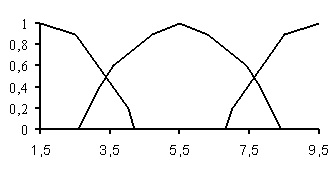
Изображения заданных функций принадлежности приведены на рисунке 3 для равномерного распределения, и на рисунке 4 для неравномерного раcпределения.
|
|
|
|
Рис. 3. Функции принадлежности с равномерным распределением термов |
Рис. 4. Функции принадлежности с неравномерным распределением термов |
2.2 Задание нечеткой системы правил
Для создаваемой системы должны быть заданы 25 правил. Эти правила приведены в таблице 3.
|
Таблица 3. Нечеткая система правил |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Затем необходимо добавить ещё 10 правил и сравнить полученные характеристики для 25 и 37 правил с заданной зависимостью. При правильном построении нечеткой системы характеристика с 37 правилами будет лучше совпадать с заданной зависимостью. Дополнительные правила приведены в таблице 4.
|
Таблица 4. Дополненная нечеткая система правил |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.3 Вывод результатов
Для того, чтобы полученные результаты было удобно визуально сравнивать друг с другом и с заданной зависимостью, все полученные графики приведены в этом разделе:
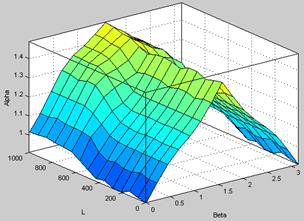
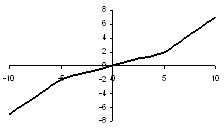
· на рисунке 5 показан график зависимости, использующей равномерно распределенные ФП и 25 правил;
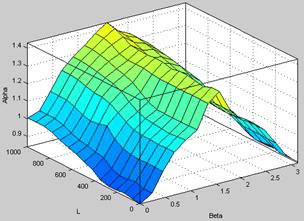
· на рисунке 6 показан график зависимости, использующей неравномерно распределенные ФП и 25 правил;
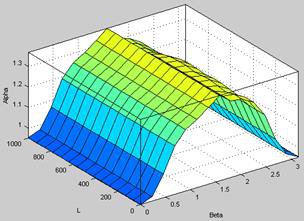
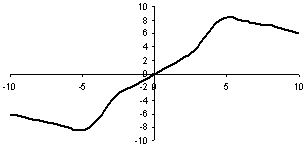
· на рисунке 7 изображен график зависимости, использующей неравномерно распределенные ФП и 37 правил;
· на рисунке 8 изображена исходная зависимость, рассчитанная аналитически.
|
|
|
|
Рис.5. Равномерно распределенные ФП, 25 правил |
Рис.6. Неравномерно распределенные ФП, 25 правил |
|
|
|
|
Рис.7. Неравномерно распределенные ФП, 37 правил |
Рис.8. Зависимость, рассчитанная аналитически |
Из рисунков видно, что распределение функций принадлежности с учетом характера аппроксимируемой зависимости и увеличение числа правил позволяют сгладить результирующую характеристику.
2.3 Анализ ошибок
Для всех трех вариантов нечетких систем рассчитаны средние ошибки по 10 точкам. Точки брались одни и те же для каждой системы. Результаты приведены в таблице 5.
Таблица 5. Средние ошибки для всех вариантов нечетких систем
|
№ |
распределение ФП |
число правил |
средняя ошибка, рад |
|
1 |
равномерное |
25 |
0,1520 |
|
2 |
неравномерное |
25 |
0,1463 |
|
3 |
неравномерное |
35 |
0,1446 |
Как видно из таблицы, увеличение точности нечеткой системы происходит не только при учете характера заданной зависимости при выборе ФП, но и при увеличении числа правил. Однако сама степень увеличения точности (уменьшения средней ошибки) невелика - около 4 % при смене распределения ФП с равномерного на неравномерное, и затем около 1,2 % при увеличении количества правил.
Вывод
В ходе лабораторной работы построена система нечеткого вывода для задачи стрельбы в заданную точку на поверхности горы. Данная задача имеет довольно громоздкое аналитическое решение в нескольких вариантах, поэтому, при условии, что нам известно некоторое количество точек для искомой зависимости (например, полученное эмпирически), решение с помощью системы нечеткого вывода может оказаться более эффективным. Точнее об эффективности можно судить, зная требуемую точность решения, а также количество, точность и распределение исходных точек. Чем меньшая точность требуется, и чем большее количество (и точность, и диапазон) исходных точек мы имеем, тем решение с помощью системы нечеткого вывода будет точнее.
На точность решения с помощью нечетких систем также влияет выбор функций принадлежности термов входных и выходных переменных и количество заданных правил. При выборе ФП следует учитывать характер искомой зависимости, если о нём что-либо достоверно известно. Также следует соблюдать внимательность при задании правил, поскольку слишком большое их количество может содержать противоречия и в итоге привести к ухудшению точности.
В данной работе изменение распределения ФП и увеличение количества правил увеличили точность системы незначительно.
Похожие материалы
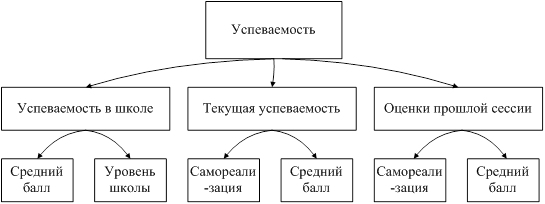
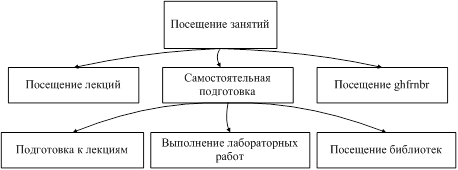
... отдаетесь учебе? YTS · Yes · No На основе этих данных построим базу знаний продукционной модели с помощью простой конструкции : Если (условие), то (действие), Набор правил для экспертной системы прогнозирования сдачи сессии студентами на основании текущей успеваемости: 3. If LIO=”Yes” and LIK=”Yes” then LI = “Yes” 4. If LIO=”Yes” and LIK=”No” then LI = “Yes” 5. If LIO=”No” ...
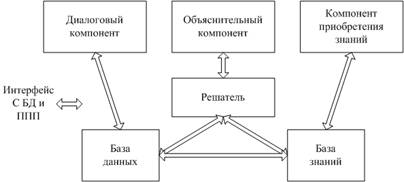
... выходных лингвистических переменных. С помощью правил преобразования дизъюнктивной и конъюнктивной формы описание системы можно привести к виду: L1 : если <A1 > то <B1 >, L2 : если <A2 > то <B2 >, .................... Lk : если <Ak > то <Bk >, где A1,A2,..,Ak - нечеткие множества, заданные на декартовом произведении X универсальных множеств входных ...
... имеет более высокие показатели качества, чем существующие аналоги, а именно она обладает более высокой степенью точности, экономичности и быстродействия. Так же проектируемая система управления подъемно-транспортным механизмом позволяет существенно обезопасить производство и труд рабочих, что в свою очередь непременно скажется на экономических показателях. Данная разработка снизит затраты на ...
... первый взгляд кажутся монотонными). Как показал анализ эта немонотонность обусловлена способом дефаззификации. Таким образом, целесообразно при построении нечётких систем управления пользоваться не только знаниями эксперта, но также базовыми понятиями теории автоматического управления. Дать общие рекомендации относительно выбора того или иного базиса не представляется возможным – все зависит от ...
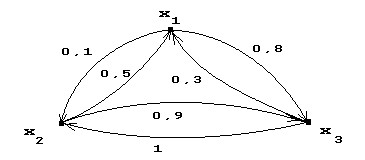
... . Для примера “если x маленькое, то y большое” (или , где знак означает операцию нечеткой метаимпликации) можно построить нечеткое отношение R следующим образом: y1 y2 y3 y4 x1 0 0,1 0,6 1 R= x2 0 0,1 0,6 0,6 x3 0 0,1 0,1 0,1 x4 0 0 0 0 В качестве элементов матрицы R записаны значения , вычисленные по ...
... финансового анализа Нами, специалистами консультационной группы "Воронов и Максимов", разработан новый комплексный показатель финансового анализа на основании результатов теории нечетких множеств. Схема построения показателя следующая: 1. Полное множество состояний А предприятия разбивается на пять (в общем случае пересекающихся) нечетких подмножеств вида: А1 - нечеткое подмножество состояний ...

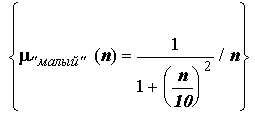
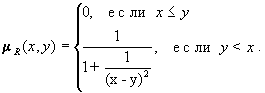

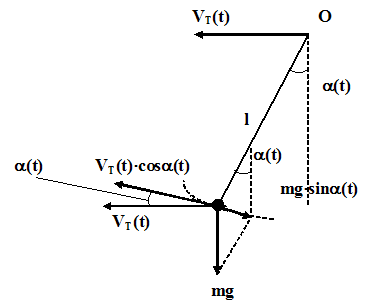

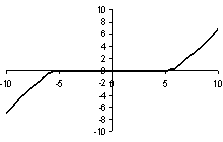
0 комментариев