ЛЕКЦИЯ 8.
ЭНТРОПИЯ. ВТОРОЙ, ОБЪЕДИНЁННЫЙ
И ТРЕТИЙ ЗАКОНЫ ТЕРМОДИНАМИКИ
Объективные причины введения понятия энтропии
Долгое время признаком наличия теплообмена считалось только изменение Т ТС или ОС либо обеих вместе. Однако практика показала, что это не совсем так. Например, при кипении воды к ней постоянно подводится тепло, то есть происходит теплообмен, а Т кипящей воды и опущенного в воду, например, бытового электрического кипятильника остаются неизменными в течение всего процесса кипения. Более того, если быстро сжимать газ в цилиндре с холодными стенками, то в результате теплообмена с ними газ отдаёт часть своего тепла и должен охлаждаться. Однако Т газа в результате совершения внешней механической работы не уменьшается, а растёт.
Все эти факты предопределили необходимость появления в термодинамике такой физической величины или функции, изменение которой указывало бы на наличие процесса теплообмена вне зависимости от того, изменяется или не изменяется температура ТС и ОС. Причём никакие другие воздействия, кроме теплообмена, не могли бы изменить значение этой физической величины. Такая функция была найдена и введена в обращение в 1865 г. Р. Клаузиусом после глубокого научного анализа изменений, наблюдаемых в ТС при обмене теплом. Она была названаэнтропией (от греческого слова tropos - мера преобразования или превращения), что свидетельствует о том, что энтропия предназначена для исследования процессов преобразования (превращения) энергии в ходе ТП. Как показали дальнейшие исследования, энтропия имеет ключевое значение для понимания основных положений термодинамики.
Главная трудность в понимании физического смысла энтропии состоит в том, что энтропия не оказывает воздействия на измерительные приборы и поэтому её нельзя измерить как, например, температуру. Изменение энтропии можно лишь вычислить по изменению тех параметров, которые доступны для непосредственного измерения в ТС. Оказалось, что таковыми могут быть основные термодинамические параметры Р, Т, v. Величины этих параметров в рассматриваемом состоянии ТС не зависят от того, каким путём ТС пришла в это состояние. Следовательно, энтропия должна быть функцией состояния ТС. Доказательство этого вывода будет приведено ниже.
Энтропия идеального газа
Как уже указывалось ранее, тепло Q не является функцией состояния ТС и поэтому dQ не может быть полным дифференциалом. Для того чтобы проинтегрировать правую часть уравнения 1-го закона термодинамики (5.3.3), необходимо знать характер ТП, то есть вид зависимости P(V ). В высшей математике доказывается, что дифференциальный двучлен, каковым является правая часть (5.3.3), всегда можно превратить в полный дифференциал путём деления (умножения) на так называемый интегрирующий делитель (множитель). Было определено, что таким делителем для элементарного количества тепла dQ является абсолютная температура Т. В этом легко удостовериться на примере идеального газа.
Согласно уравнению Клапейрона вида PV = MRT, где М = const, имеем P = MRT/V. Если теперь в правой части уравнения (5.3.12), записанном для произвольной массы газа, заменить P на MRT/V и разделить обе его части на Т, то получим:
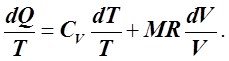 (6.2.1)
(6.2.1)
Из (6.2.1) следует, что dQ/T при обратимых ТП (отсутствуют потери энергии) есть полный дифференциал некоторой функции, зависящей только от двух основных термодинамических параметров T и V. Действительно, СV идеального газа зависит только от T, а М и R также величины постоянные. Таким образом, левая часть (6.2.1) зависит только от абсолютных величин T и V и не зависит от характера их изменения в ТП. Эту функцию Клаузиус назвал энтропией и обозначил буквой S.
В связи с тем, что T и V(v) определяют состояние ТС, то S является функцией состояния этих систем. Термин энтропияв настоящее время довольно широко стал использоваться и в других отраслях науки и техники, например, энтропия погрешности измерения, поэтому в термодинамике всё чаще стал использоваться термин термодинамическая энтропия.
Таким образом, дифференциал энтропии для обратимого ТП определяется как
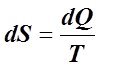 или
или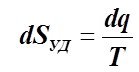 , (6.2.2)
, (6.2.2)
где dQ – элементарное количество тепла, подведённого к ТС (отведённого от неё) в ходе ТП, Дж; dSУД – удельная энтропия, Дж/(кг×К); [S] = Дж/К; Т – абсолютная температура, К, источника тепла.
Так как ТП – процесс обратимый, то это предполагает бесконечно малую разность температур между ТС и источником тепла. Поэтому в (6.2.2) Т также является и абсолютной температурой ТС.
Из (6.2.2) следует, что dQ = TdS и, следовательно, получаем, чтодля каждой ТС существует физическая величина, значение которой зависит только от состояния системы (следовательно, она является функцией состояния системы) и изменение которой в равновесных ТП происходит только под действием энергии, передаваемой в ходе этих ТП в виде тепла. Эта физическая величина, как уже отмечалось выше, и была названа энтропией.
Отношения dQ/T и Q/T также получили название в термодинамике соответственно элементарного приведённого теплаи приведённого тепла.
Уравнение (6.2.2) представляет собой математическое выражение
2-го закона термодинамики для обратимых ТП, который подробнее будет рассмотрен ниже. Таким образом, дифференциал энтропии dS представляет собой элементарное приведённое тепло, полученное телом при обратимом ТП.
В том, что dS является полным дифференциалом, можно также убедиться, проинтегрировав (6.2.1):
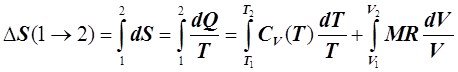 , (6.2.3)
, (6.2.3)
где DS(1®2) – изменение энтропии ТС при её переходе из начального 1 в конечное 2 состояние; Т1, V1, Т2, V2 - температура, К, и объём, м3, газа соответственно в начальном и конечном состояниях ТС.
В связи с тем, что теплоёмкость идеального газа не зависит от давления Р, можно воспользоваться в (6.2.3) понятием средней изохорной теплоёмкости в диапазоне температур от Т1 до Т2, что предопределяет ![]() . Тогда получаем:
. Тогда получаем:
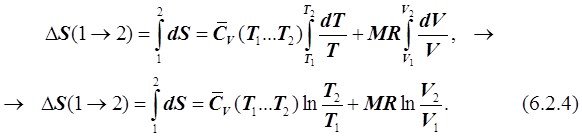
В результате интегрирования получаем, что правая часть второго уравнения (6.2.4) зависит только от параметров начальных Т1 и V1 и конечных Т2 и V2 состояний газа и не зависит от того, в ходе какого ТП произошло изменение состояния газа. Таким образом, действительно dS является полным дифференциалом и, следовательно, изменение энтропии идеального газа в ходе ТП может быть определено как:
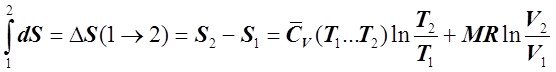 . (6.2.5)
. (6.2.5)
Из (6.2.5) следует, что S является однозначной функцией состояния ТС, принимающей для каждого её состояния строго определённое значение, определяемое параметрами ТС в её крайних (начальных и конечных) состояниях.
ЭнтропияS так же, как энтальпия I и внутренняя энергия U, является экстенсивным параметром, так как её величина, как видно из (6.2.5), пропорциональна массе ТС. Интенсивными параметрами являются удельная, Sуд = S/M, и молярная, Sm = S/nm = Sудm, энтропии. Соответственно [Sm] =
= Дж/(моль×К). В технических расчётах в термодинамике в большинстве случаев используется Sуд, которую в основном в дальнейшем и рассмотрим.
При равновесном (обратимом) ТП параметры состояния равновесной ТС изменяются во всех её точках одинаково. Кроме того:
![]() (6.2.6)
(6.2.6)
где ![]() - изменение количества тепла в отдельных частях ТС в ходе ТП, Дж.
- изменение количества тепла в отдельных частях ТС в ходе ТП, Дж.
Разделив обе части (6.2.6) на Т, являющейся одинаковой для всех частей ТС, получаем:
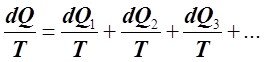 или
или ![]() (6.2.7)
(6.2.7)
где ![]() - изменение полной энтропии всей ТС и её отдельных частей в ходе ТП, Дж/К.
- изменение полной энтропии всей ТС и её отдельных частей в ходе ТП, Дж/К.
Из (6.2.7) следует, что S обладает свойством аддитивности, то есть алгебраическая сумма изменений энтропии отдельных частей ТС будет равна изменению энтропии всей ТС. Причём если ТС будет гетерогенной, то изменение S отдельных её частей в зависимости от хода ТП могут быть как положительными, так и отрицательными величинами. По отношению к газовой смеси это означает, что полная энтропия S идеальной газовой смеси равна сумме энтропий Si газовых компонентов, взятых при тех параметрах, который каждый из компонентов имеет в смеси, то есть при температуре смеси Тi = Тсм и парциальных давлениях РП,i компонентов.
Поскольку S, а соответственно Sуд и Sm , является функцией состояния ТС, то она может быть определена как функция основных термодинамических параметров (трёх или двух):
![]()
Для замкнутых обратимых ТП (обратимых циклов), когда ТС самостоятельно возвращается в своё первоначальное состояние:
![]() (6.2.8)
(6.2.8)
В термодинамике интеграл по замкнутому контуру цикла от элементарного приведённого тепла называется уравнением Клаузиуса или первым интегралом Клаузиуса, который впервые предложил его в таком виде.
При нагревании ТС dQ > 0, а при охлаждении dQ < 0. Следовательно, как следует из (6.2.2), S возрастает при поступлении тепла в ТС, dS > 0, и уменьшается при отводе тепла из неё, dS < 0.
Из (6.2.2) следует, что в адиабатных ТП (dQ = 0) dS= 0, то есть в этих процессах энтропия является постоянной величиной. Также dS = 0 и при протекании любых обратимых ТП в изолированной ТС, которая по определению не обменивается с ОС ни энергией (dQ = 0, dLд = 0), ни веществом.
Учитывая, что dq = TdSуд , определим q как
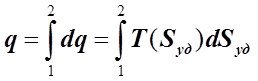 , (6.2.9)
, (6.2.9)
где T(Sуд) - зависимость абсолютной температуры ТС от её удельной энтропии, К.
Соответственно, чтобы так определять величину q, необходимо знать вид зависимости T(Sуд). В изотермическом ТП (Т = const) имеем:
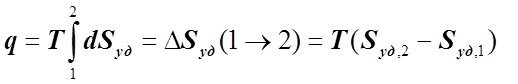
или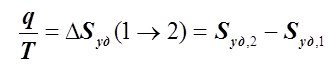 . (6.2.10)
. (6.2.10)
Следовательно, при фазовых превращениях 1-го рода, происходящих при Т = const, например плавлении или испарении породы или любого другого твёрдого или жидкого вещества, изменение энтропии будет:
 , (6.2.11)
, (6.2.11)
где ![]() - удельная энтропия вещества в моменты начала и конца процесса его плавления или испарения, Дж/(кг×К);
- удельная энтропия вещества в моменты начала и конца процесса его плавления или испарения, Дж/(кг×К); ![]() ,
, ![]() - удельная энтальпия соответственно плавления и испарения вещества, Дж/кг; Тпл , Тисп – абсолютная температура плавления и испарения вещества, К.
- удельная энтальпия соответственно плавления и испарения вещества, Дж/кг; Тпл , Тисп – абсолютная температура плавления и испарения вещества, К.
Фазовыми превращениями 1-го рода называют процессы, сопровождающиеся поглощением или выделением тепла и изменением объёма, в которых происходит изменение агрегатного состояния вещества или переход из одного твёрдого состояния в другое. Соответственно, в результате этих превращений происходит скачкообразное изменение ряда свойств вещества.
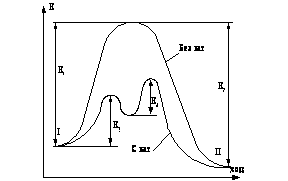
Графическое изображение зависимости Т = f(S) или Т = f(Sуд) представляет собой так называемую энтропийную диаграмму (ТS – диаграмма, тепловая диаграмма).
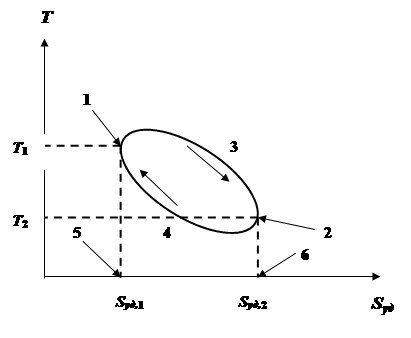
 Величина площади под кривой ТП 1-3-2 будет равна в соответствующем масштабе количеству тепла, поступившего в ТС в ходе этого ТП, то есть
Величина площади под кривой ТП 1-3-2 будет равна в соответствующем масштабе количеству тепла, поступившего в ТС в ходе этого ТП, то есть
q1-2-3 = S1-3-2-6-5-1. Следует обратить внимание, что температура ТС в этом ТП уменьшается и на поступление тепла в ТС указывает только характер изменения энтропии, которая в ходе ТП увеличивается.
В заключение следует отметить, что введение понятия энтропии было рассмотрено применительно к идеальному газу. Однако выполненными исследованиями убедительно доказано, что понятие энтропии распространяется и на реальные вещества независимо от их свойств, то есть формула (6.2.2) справедлива как для идеальных газов, так и для реальных веществ.
Изменение энтропии в неравновесных
термодинамических процессах
Особенно легко характер изменения S в необратимых ТП можно выявить при рассмотрении этих процессов в изолированных ТС. В этих ТС согласно 1-го закона термодинамики имеем:
![]() . (6.3.1)
. (6.3.1)
Следовательно, в таких ТС U = const даже в необратимых ТП. Учитывая, что в этих ТС может иметь место обмен теплом, работой и веществом между их отдельными частями, рассмотрим ТС, состоящую из 2-х частей, имеющих Т = Т1 и Т = Т2, причём Т1 > Т2. В этом случае Q из 1-й части ТС будет переходить во 2-ю. Следовательно, S 1-й части ТС будет уменьшаться на ![]() , а 2-й - увеличиваться на
, а 2-й - увеличиваться на ![]() . В связи с тем, что S обладает свойством аддитивности, изменение S всей ТСбудет равно алгебраической сумме dS1 и dS2:
. В связи с тем, что S обладает свойством аддитивности, изменение S всей ТСбудет равно алгебраической сумме dS1 и dS2:
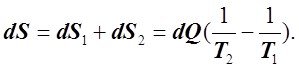 (6.3.2)
(6.3.2)
Учитывая, что Т1 > Т2 , получаем dS > 0 или в интегральной форме
S2 > S1. Это говорит о том, что S веществ в необратимых ТП, протекающих в изолированных ТС, всегда возрастает. Это положение представляет собой наиболее общую формулировку 2-го закона термодинамики для неравновесных ТП, известную под названием принципа возрастания энтропии (закона возрастания энтропии) при неравновесных ТП.
Ранее было доказано, что при обратимых (равновесных) ТП в изолированных ТС имеет место dS = 0 и соответственно dS = dQ/T. Поэтому неравенство dS > 0 предопределяет и неравенство dS > dQ/T. Последние неравенства показывают, что при необратимых ТП изменение S изолированных ТС всегда больше изменения их S при обратимых ТП.
В общем случае имеем:
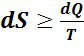 или
или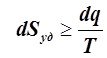 ,
,![]() (6.3.3)
(6.3.3)
где dQ, dq - элементарное количество тепла, Дж, удельного тепла, Дж/кг, поступающего в ТС от источника тепла с абсолютной температурой Т, К. Необходимо иметь в виду, что и в (6.2.2), и в (6.3.3) Т есть абсолютная температура источника тепла, однако в (6.2.2) Т может рассматриваться и как абсолютная температура ТС, так как разница между температурами ТС и источника тепла составляет бесконечно малую величину. В (6.3.3), как и далее, знак равенства относится к обратимым ТП, а знак «больше» - к необратимым.
Выражение (6.3.3) есть аналитическое выражение 2-го закона термодинамики для любых ТП. Из него следует, что если отсутствует внешнее воздействие, то ТП, протекающие в изолированных ТС самопроизвольно без совершения механической работы, либо не изменяют энтропию этих систем, если ТП обратимые, либо увеличивают её, если ТП необратимые. В связи с тем, что все реальные ТП являются в той или иной степени необратимыми, 2-ой закон термодинамики по Клаузиусу был сформулирован следующим образом: энтропия изолированной ТС всегда стремится к максимуму.
Следует иметь в виду, что энтропия отдельных тел в системе может и уменьшаться, и увеличиваться, и оставаться постоянной под влиянием происходящих в ней процессов. Однако общая энтропия изолированной системы при необратимых процессах будет только увеличиваться. Для уменьшения энтропии этой системы необходимо передать тепло от более холодного тела более тёплому телу, что возможно только при затрате энергии извне, например при затрате механической энергии, как это делается в холодильниках.
Таким образом, закономерность изменения S в изолированных ТС выражает необратимость и односторонность макроскопических ТП в них, а сама S является, во-первых, критерием направления реальных процессов, происходящих в этих ТС, и, во-вторых, мерой необратимости каждого из этих ТП. Из последнего следует, что степень необратимости ТП в изолированных ТС количественно характеризуется приращением S в результате этих ТП.
Численное значение S можно рассматривать как показатель большего или меньшего приближения изолированной ТС к равновесному состоянию, а значит и возможности протекания в ней ТП. Когда в изолированной ТС S = max, то в ней не могут протекать самопроизвольные ТП, потому что любой такой ТП необратим и сопровождается увеличением S, которая уже достигла максимальной величины. Поэтому состояние изолированной ТС с S = max является состоянием её устойчивого равновесия.
Математические выражения 1-го и 2-го законов термодинамики можно объединить в одно уравнение. Для закрытых ТС для 1 кг вещества имеем: и dq = du + dlд = du + Рdv. Учитывая, что
и dq = du + dlд = du + Рdv. Учитывая, что ![]() , получаем:
, получаем:
TdSуд³ du + Рdv. (6.3.4)
Используя второй вид уравнения 1-го закона термодинамики, получаем:
TdSуд ³ di - vdР. (6.3.5)
Эти соотношения, охватывающие 1-ый и 2-ой законы термодинамики, получили название объединённого закона термодинамики для закрытых ТС. Соответственно они применимы как для обратимых, так и необратимых ТП.
Вычисление энтропии веществ
Способов непосредственного измерения энтропии не существует. Энтропия S веществ, в каком либо конечном состоянии 2 по отношению к некоторому начальному состоянию 1 в общем виде вычисляется путём суммирования приведённого тепла, сообщённого веществам при обратимом переходе их из состояния 1 в состояние 2. Причём это справедливо как для равновесных, так и неравновесных ТС.
Если при переходе вещества из состояния 1 при Т = 0 К в состояние 2 отсутствуют фазовые переходы, то абсолютное значение энтропии вещества S определяется интегрированием (6.2.2):
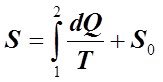 , (6.4.1)
, (6.4.1)
где S0 – постоянная интегрирования, физический смысл которой – энтропия вещества при абсолютном нуле, Дж/К.
При температурах, близких к абсолютному нулю, все известные вещества находятся в конденсированном состоянии. Для таких веществ В. Нернст в 1906 г. экспериментально установил, а М. Планк в 1912 г. окончательно сформулировал следующий принцип: при температуре близкой к абсолютному нулю энтропия вещества, находящегося в конденсированном состоянии с упорядоченной структурой, стремится к нулю, то есть S0 = 0 при T1 = 0 К. Этот закон называют 3-м законом термодинамики, или тепловой теоремой Нернста.
Абсолютная величина S необходима для расчёта процессов, сопровождающихся изменением массы исходных веществ и образованием новых, например, при химических реакциях. В технической термодинамике обычно используют не абсолютное значение энтропии S, а её изменение в каком-либо процессе перехода ТС из состояния 1 в состояние 2, то есть ![]() , которая при отсутствии фазовых переходов вычисляется как:
, которая при отсутствии фазовых переходов вычисляется как:
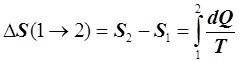 или
или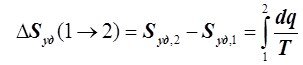 . (6.4.2)
. (6.4.2)
Выражение для расчёта изменения энтропии идеального газа, а соответственно и всех газов и газовых смесей, которые в рассматриваемых ТП могут считаться идеальными газами, как функции Т и V получено выше (см. 6.2.5). Оно легко может быть записано для 1 кг газа.
В связи с тем, что Р, Т и v связаны между собой уравнением Клапейрона, можно получить выражения для расчётов DSуд(1®2) как функции и других основных термодинамических параметров.
Для получения DSуд(1®2) как функции Р и Т следует из уравнения (6.2.1), записанного для 1 кг идеального газа, исключить v. Из уравнения Клапейрона после дифференцирования получим:
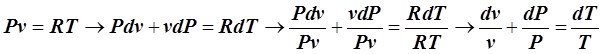 .(6.4.4)
.(6.4.4)
Подставив 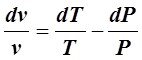 в (6.2.1), получаем:
в (6.2.1), получаем:

Интегрируя (6.4.5) при ![]() , получим:
, получим:
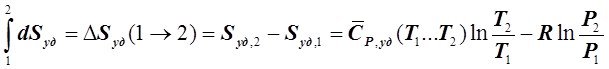 .(6.4.6)
.(6.4.6)
Для получения DSуд(1®2) как функции Р и v следует из (6.2.1), записанного для 1 кг идеального газа исключить Т. Пользуясь тем же методом, получим:
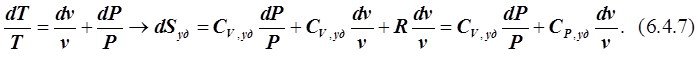
Интегрируя, получаем:
 . (6.4.8)
. (6.4.8)
На первый взгляд СР,уд и СV,уд в (6.4.8) должны быть усреднены в диапазонах соответственно от v1 до v2 и от Р1 до Р2. Однако удельные теплоёмкости веществ не являются функцией их плотности, а соответственно и связанного с ней обратной зависимостью удельного объёма v, так как эти теплоёмкости относятся к 1 кг веществ вне зависимости от того, какой объём занимает этот килограмм.СР,уд и СV,уд не могут также быть и функцией Р, так как теплоёмкости идеальных газов не зависят от давления. Однако в ходе ТП изменяются не только v и Р, но и Т вещества, поэтому в (6.4.8) необходимо использовать СР,уд и СV,уд, взятые не при какой-то конкретной Т, а усреднённые в соответствующем диапазоне температур от Т1 до Т2, не обращая внимание на изменение v и Р в ходе ТП.
Учитывая, что изменение энтропии веществ не зависит от характера ТП, полученные уравнения (6.4.3), (6.4.6) и (6.4.8) можно применять как для обратимых, так и для необратимых процессов.
Обычно в теплотехнических расчётах начальное значение энтропии идеальных газов Sуд,1 = 0 принимают в том же состоянии, которое принято за нуль отсчёта энтальпии и внутренней энергии. Как правило, это нормальные физические условия. При таком начале отсчёта энтропия идеальных газов может быть найдена как:
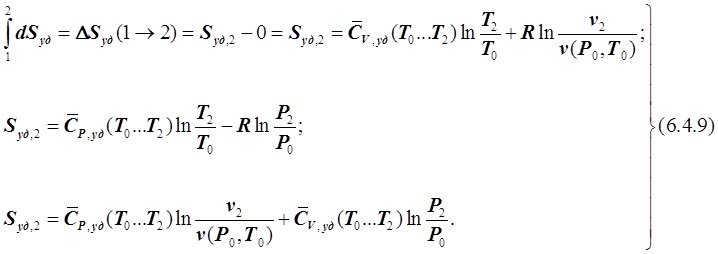
У жидких и твёрдых веществ влияние Р и Т на их v очень мало. Поэтому в изобарном ТП точно, а в других с очень небольшой погрешностью для этих веществ имеем dq = CP,удdT (см. 5.4.18). Следовательно, у этих веществ изменение энтропии при переходе из состояния 1 в состояние 2 можно определять следующим образом:
при отсутствии фазовых превращений
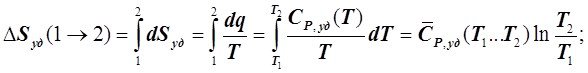 (6.4.10)
(6.4.10)
при наличии фазовых превращений, происходящих при T = const, например плавления и испарения, в диапазоне температур от Т1 до Т2, причём, когда Т1 < Тпл, а Т2 > Тисп:
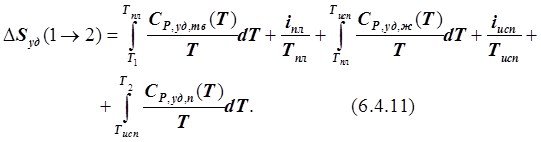
Для ряда веществ при стандартных условиях их состояния в химической термодинамике в настоящее время экспериментально определены абсолютные величины удельной и молярной энтропий Sm и Sуд. Они получили название стандартной удельной энтропиии обозначение ![]() . При известной величине
. При известной величине ![]() абсолютная удельная энтропия вещества при Т2 > 298,15 К, то есть
абсолютная удельная энтропия вещества при Т2 > 298,15 К, то есть ![]() , и отсутствии фазовых превращений определяется следующим образом:
, и отсутствии фазовых превращений определяется следующим образом:
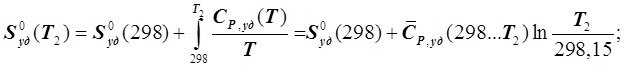 (6.4.12)
(6.4.12)
Значение и основные положения второго закона термодинамики проработать самостоятельно (см. 6.5. Части 3).
Похожие работы
... большой материал, предусмотренный программой. Преимущество такого подхода к рассмотрению отдельных, или группы, вопросов, как показали наши наблюдения, не вызывает сомнений как с точки зрения корректности математических выражений, так и логичности и взаимосвязи явлений термодинамики. СОСТАВЛЕНИЕ ДЕТЕРМИНАНТОВ ЯКОБИ И ТАБЛИЦЫ ТЕРМОДИНАМИЧЕСКИХ КОЭФФИЦИЕНТОВ ДЛЯ СИСТЕМ, ОПИСЫВАЕМЫХ БОЛЬШИМ ...
... морской капусты. От трилобитов отщепляется веточка, развившаяся в подтип хелицеровые (ныне полнее всего представленная паукообразными). Их наиболее древние представители - ордовикские ракоскорпионы - мало отличаются от современных скорпионов. Они первыми вышли на сушу. В кембрийские и ордовикские времена жизнь существовала в основном в море, высшие формы жизни – исключительно в море. Следующий ...
... с кислородом, восстановлением - отнятие кислорода. С введением в химию электронных представлений понятие окислительно-восстановительных реакций было распространено на реакции, в которых кислород не участвует. В неорганической химии окислительно-восстановительные реакции (ОВР) формально могут рассматриваться как перемещение электронов от атома одного реагента (восстановителя) к атому другого ( ...
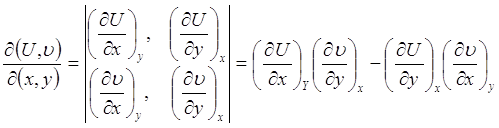
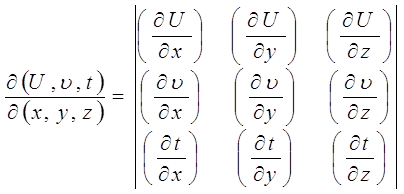
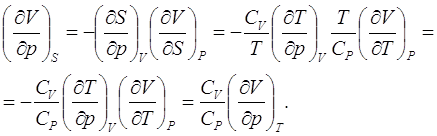
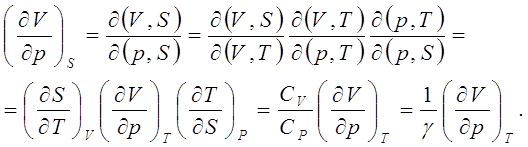
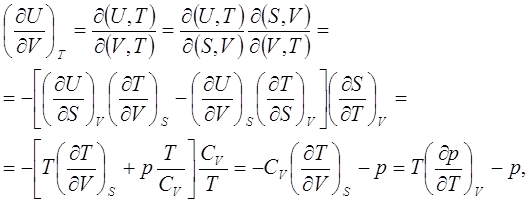
0 комментариев