Навигация
Изучение некоторых вопросов термодинамики
ГЗОГЯН В. М.
ИЗУЧЕНИЕ НЕКОТОРЫХ ВОПРОСОВ ТЕРМОДИНАМИКИПособие для студентов физических специальностей
Применяется метод решения задач, основанный на использовании якобианов, который позволяет легко перейти от недоступных измерению величин к доступным.
Приведены примеры решения подобных задач, для которых получены общие дифференциальные соотношения, позволяющие анализировать полученные выражения для идеальных и реальных систем. Показано, что одно и то же значение частной производной, при постоянном значении выбранного параметра, можно получить несколькими способами, в зависимости от выбора промежуточных переменных. Это даёт возможность, с одной стороны, проверить правильность полученных соотношений, а с другой, ввести в рассмотрение такие новые якобианы, тождественно равные единице, которые относительно быстро приводят к решению задачи.
Пособие может быть рекомендовано студентам физических специальностей высших учебных заведений, желающих углубить свои знания в данной области, и использовано ими в учебно-исследовательской работе при составлении и решении новых задач и интерпретации полученных соотношений.
КРАТКОЕ ВВЕДЕНИЕПерестройка программы высших учебных заведений по общей и теоретической физике предполагает усовершенствование методов изучения отдельных вопросов и разделов, а также и методов решения задач. Это усовершенствование должно позволить студентам не только глубже усвоить физическое содержание рассматриваемого вопроса, но и видеть взаимосвязь между изучаемыми явлениями.
При изучении ряда вопросов и решении части задач термодинамики часто приходится производить преобразование термодинамических величин, например, преобразования переменных, поддерживаемых постоянными в ходе процесса, другими. Такие преобразования нужно совершать по общим правилам замены переменных при дифференцировании функций по нескольким переменным. [1].
Один из способов преобразования термодинамических величин приведен в [1]. Однако преобразования величин целесообразно производить методом якобианов, но для этого необходимо ознакомить студентов с якобианами и их свойствами [2].
Якобианом называется определитель
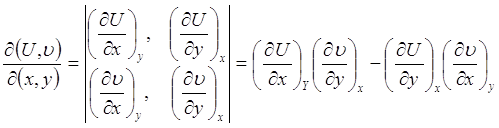
причем такой символ следует рассматривать как единый, а U и υ – как функции Х и У.
Якобиан обладает следующими важными свойствами:
1. 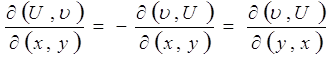
2. 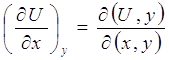
3. 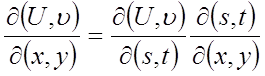
4. 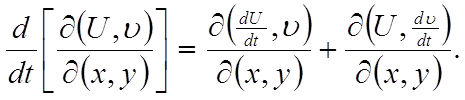
Если система может быть описана тремя независимыми переменными, например, в случае системы с переменным количеством вещества, то целесообразно использовать якобиан вида:
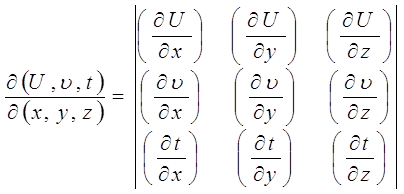 ,
,
который раскрывается как определитель третьего порядка. Для систем с четырьмя независимыми переменными, якобиан раскрывается как определитель четвертого порядка и т. д.
Таким образом, в термодинамике, согласно [3], существует такое множество соотношений, что не имеет смысла их запоминать. Лучше запомнить лишь термодинамическое тождество, объединяющее первое и второе начала, определения термодинамических потенциалов и какое-нибудь правило преобразования одного набора переменных в другой, что легко осуществить составлением детерминантов Якоби.
Применение якобианов, с одной стороны, позволяет устанавливать связь между термодинамическими величинами (коэффициентами) наиболее простым способом, а с другой – даёт возможность легко перейти от недоступных измерению величин к доступным.
ТЕРМОДИНАМИЧЕСКИЕ КОЭФФИЦИЕНТЫ И УСТАНОВЛЕНИЕ СВЯЗИ МЕЖДУ НИМИ.Согласно [4], термодинамическими коэффициентами называются выражения вида 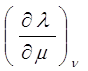 , где символами l, m, n обозначены р, V, Т, S. Эти коэффициенты характеризуют определённые свойства системы.
, где символами l, m, n обозначены р, V, Т, S. Эти коэффициенты характеризуют определённые свойства системы.
 Составим таблицу термодинамических коэффициентов так, чтобы первая строка не содержала S, вторая – Р, третья – V и четвертая – Т:
Составим таблицу термодинамических коэффициентов так, чтобы первая строка не содержала S, вторая – Р, третья – V и четвертая – Т:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Можно показать, что если четыре из них, подчеркнутых в таблице, выбрать в качестве независимых коэффициентов, то остальные восемь могут быть выражены через них. Действительно, нетрудно заметить, что произведение коэффициентов, стоящих в одной строке данной таблицы, равно минус единице. Например, для первой строки
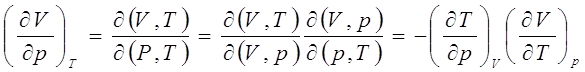
Разделив обе части данного выражения на 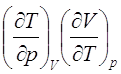 , получим
, получим
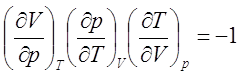 (2.2)
(2.2)
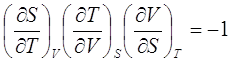 (2.3)
(2.3)
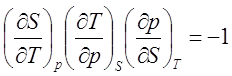 (2.4)
(2.4)
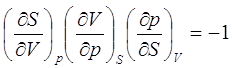 (2.5)
(2.5)
 Ещё четыре соотношения между термодинамическими коэффициентами можно получить из выражений для дифференциалов термодинамических функций
Ещё четыре соотношения между термодинамическими коэффициентами можно получить из выражений для дифференциалов термодинамических функций
dU = TdS – pdV
![]() dF = – SdT – pdV
dF = – SdT – pdV
dI = TdS + Vdp
dФ = – SdT + Vdp
или же путем преобразования основного термодинамического тождества, справедливого для всех функций, с помощью введения новых якобианов, равных единице.
Поскольку термодинамические функции являются функциями состояния, то правые части выражений (2.6) должны удовлетворять требованиям
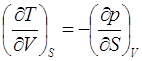 (2.7)
(2.7)
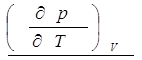 (2.8)
(2.8)
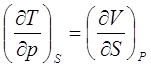 (2.9)
(2.9)
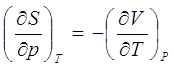 (2.10)
(2.10)
Основное термодинамическое тождество можно получить из этих выражений. Действительно, из (2.7) имеем
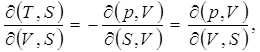
откуда
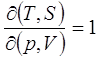 (2.11)
(2.11)
Из сказанного следует также, что выражения (2.7)—(2.10) могут быть получены из основного тождества (2.11).
После того, как записаны основные уравнения, в принципе, мы могли бы, как это сделано в [4], выбрать в (2.1) три независимых коэффициента и с помощью этих уравнений выразить оставшиеся коэффициенты через выбранные. Однако, при решении некоторых задач, такой подход оказывается менее целесообразным, так как соответствующие выражения оказываются громоздкими. Более того, мы можем принимать во внимание то обстоятельство, что если известно уравнение состояния системы, то можно легко вычислить и третий коэффициент первой строки в (2.1). Поскольку при решении большинства задач уравнение состояния системы известно, то, практически, в (2.1) можно выбрать в качестве независимых пять коэффициентов. Такой подход много упрощает решение задач.
Выразим теперь одни коэффициенты через другие с учетом вышесказанного. Во второй строке известен один коэффициент, но с помощью (2.8) найдем второй. Тогда на основании (2.8) и (2.3) найдем третий
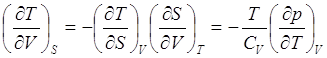 (2.12)
(2.12)
В третьей строке (2.1) известен один коэффициент. Второй коэффициент можно получить, используя свойство якобианов
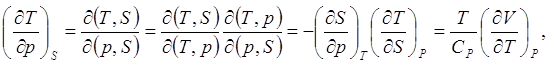 (2.13)
(2.13)
где было учтено выражение (2.10). Тогда на основании (2.4) и (2.13) найдем третий
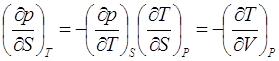 (2.14)
(2.14)
что непосредственно вытекает также из (2.10). Первый коэффициент четвертой строки легко можно найти с помощью выражений (2.9) и (2.13), или же используя свойство якобианов
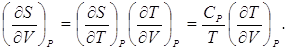 (2.15)
(2.15)
Из (2.7) с учетом (2.12) получим второй коэффициент
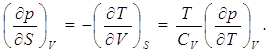 (2.16)
(2.16)
Наконец, последний коэффициент можно получить из (2.5) с учетом выражений (2.15) , (2.16) и (2.2)
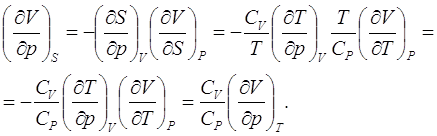 (2.17)
(2.17)
Отметим, что, в дальнейшем, при рассмотрении тех или иных вопросов, будем получать общие дифференциальные соотношения, которые позволят, зная уравнения состояния системы, обобщить их для идеальных и реальных систем.
ВЫВОД УРАВНЕНИЯ АДИАБАТИЧЕСКОГО ПРОЦЕССА ДЛЯ ИДЕАЛЬНОГО И РЕАЛЬНОГО ГАЗОВ.Процесс, протекающий при постоянной энтропии называется адиабатическим или изоэнтропным
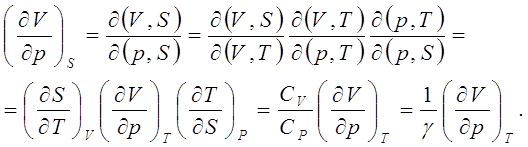
Отметим, что поскольку![]() , то
, то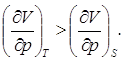 Таким образом, адиабатический процесс мы свели к изотермическому, который для идеального газа можно представить в виде:
Таким образом, адиабатический процесс мы свели к изотермическому, который для идеального газа можно представить в виде:![]() Учитывая, что для данного газа
Учитывая, что для данного газа 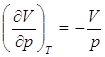 ,
получим:
,
получим:
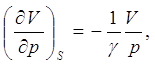
или после разделения переменных и интегрирования
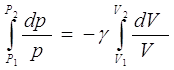 ;
; 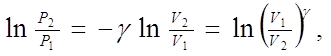
откуда ![]()
Уравнение адиабатического процесса для газа Ван-дер-Ваальса целесообразно найти из выражения
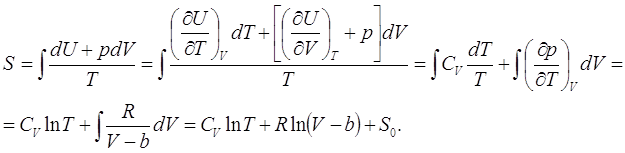
Для получения этого выражения было использовано известное в термодинамике соотношение, которое, также, легко получить с помощью якобианов
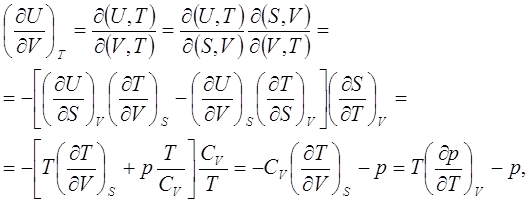 (3.1)
(3.1)
где использовано соотношение (2.12). Принимая во внимание, что для адиабатического процесса![]() , причём постоянную интегрирования
, причём постоянную интегрирования![]() , можно принять равной нулю, получим
, можно принять равной нулю, получим![]()
или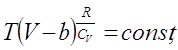
которое для переменных P и V принимает вид:
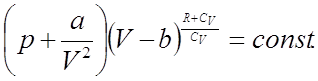
Найдем выражение для вычисления скорости распространения звука в среде, являющееся адиабатическим процессом.
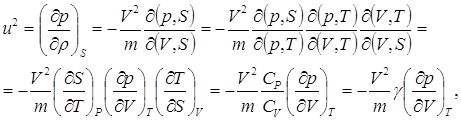
где r – плотность среды, S -энтропия, являющаяся функцией параметров P, V и T состояния системы. Этой формулой удобно пользоваться при нахождении скорости звука в газообразной среде. В частности, скорость звука в воздухе, при нормальных условиях можно найти, применяя уравнение состояния идеального газа, для которого
![]()
После подстановки этого выражения в исходную формулу получим:
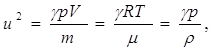
откуда ![]()
Подставляя в эту формулу численные значения g, р и r для скорости звука получим U»333 м/с.
Для определения скорости звука в жидких и твёрдых телах необходимо в выражение
![]()
подставить значения g, r и ![]() из таблиц. Например, для воды U»1400 м/с. Здесь уместно отметить, что скорость звука в морской воде, согласно [5], зависит от температуры, солёности и гидростатического давления. Необходимо также подчеркнуть, что скорость звука – важная величина, во многом характеризующая физические свойства тел. Зная скорость звука, можно определить упругие постоянные твердых тел, их зависимость от температуры, сжимаемость, отношение теплоемкостей для жидкостей и твердых тел.
из таблиц. Например, для воды U»1400 м/с. Здесь уместно отметить, что скорость звука в морской воде, согласно [5], зависит от температуры, солёности и гидростатического давления. Необходимо также подчеркнуть, что скорость звука – важная величина, во многом характеризующая физические свойства тел. Зная скорость звука, можно определить упругие постоянные твердых тел, их зависимость от температуры, сжимаемость, отношение теплоемкостей для жидкостей и твердых тел.
Теплоемкость газа при постоянном объёме определяется выражением![]() Найдём связь между изменениями внутренней энергии системы и её температуры при постоянном значении р.
Найдём связь между изменениями внутренней энергии системы и её температуры при постоянном значении р.
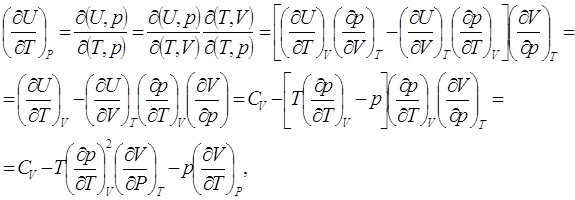 (5.1)
(5.1)
где учтены соотношения (3.1) и (2.2).
Найдём также связь между изменениями внутренней энергии системы и её температуры при адиабатическом процессе.
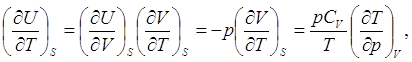 (5.2)
(5.2)
где использовано соотношение, объединяющее первое и второе начала термодинамики и выражение (2.12).
Отвлекаясь от процессов, протекающих в системе, можно показать, что для идеального газа
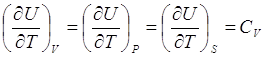
Такое же заключение для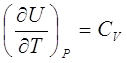 ,
,
но с помощью статистического метода сделано в [6]. Читателям представляем возможность дать удовлетворительное, с точки зрения законов термодинамики, объяснение равенства выражений (5.3).
Отметим, что для реального газа, подчиняющегося уравнению Ван-дер-Ваальса после подстановки соответствующих частных производных, при замене давления его значением, найдём
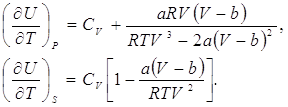
Найдём связь между изменениями энтропии и внутренней энергии
при постоянных значениях других параметров системы.
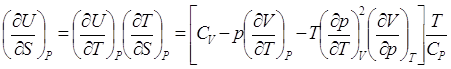 , (6.1)
, (6.1)
где использовано (5.1).
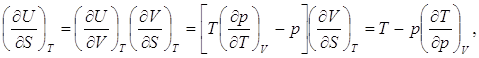 (6.2)
(6.2)
где применены формулы (3.1) и (2.8).
Из выражения (6.1) вытекает, что для идеального газа
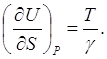 (6.3)
(6.3)
| (6.3) |
Сравнивая это значение с
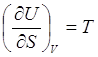 (6.4)
(6.4)
придём к выводу, что при изохорическом и изобарическом процессах одинаковому изменению энтропии соответствует неодинаковое изменение внутренней энергии. Нетрудно также заметить, что для идеального газа, согласно (6.2), изменение энтропии, связанное или с изменением объёма, или же давления, не приводят к изменению внутренней энергии.
Найдём связь между изменениями давления и внутренней энергии системы при адиабатическом, изотермическом и изохорическом процессах.
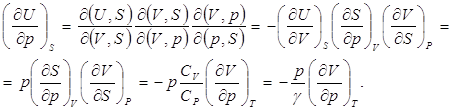 (6.5)
(6.5)
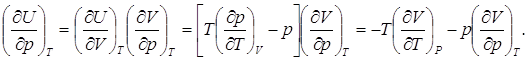 (6.6)
(6.6)
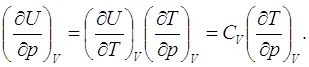 (6.7)
(6.7)
В случае идеального газа формулы (6.5) и (6.7) дают
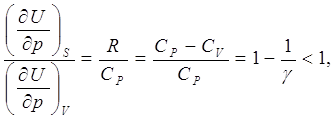
откуда 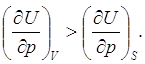 (6.8)
(6.8)
Это соотношение показывает, что при изохорическом м адиабатическом процессах одинаковому изменению давления соответствуют неодинаковые изменения внутренней энергии. Читателям представляем возможность самим выяснить физическую сущность различия этих величин. Мы только отметим, что при изохорическом процессе система не совершает работы, а изменение давления может происходить за счёт подводимого к системе или отводимого от системы количества теплоты. При адиабатическом же процессе изменение давления может быть обусловлено либо работой системы, против сил, за счет её внутренней энергии, либо же работой, совершенной над системой.
Найдём связь между изменениями объёма системы и её внутренней энергией при изобарическом процессе.
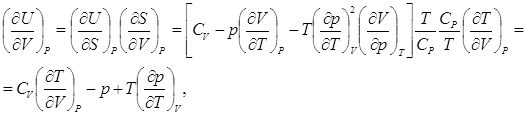 (6.9)
(6.9)
где были учтены (6.1), (2.15) и (2.2).
Для идеального газа выражение (6.9) даёт
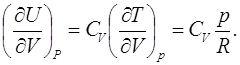 (6.10)
(6.10)
Сравним это значение с ранее полученным (3.1) и выражением
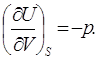 (6.11)
(6.11)
Для идеального газа, на основании (3.1),
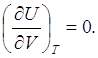
Из (6.10) и (6.11) следует:
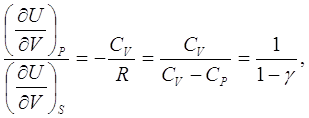
откуда
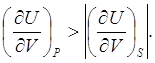 (6.12)
(6.12)
Объяснение причин различия значений этих величин должно быть подобно объяснению различия величин (6.8). Только в полученном выражении изменения объёма системы и её внутренней энергии при адиабатическом процессе имеют противоположные знаки, а при изобарическом – одинаковые.
ВЫВОД НЕКОТОРЫХ ПОЛЕЗНЫХ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ.1. Найдём разность теплоёмкостей СР и СV.
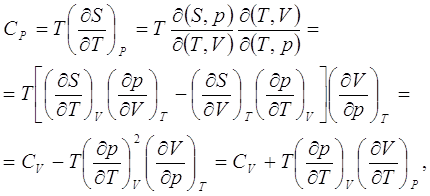
откуда
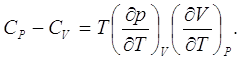 (7.1)
(7.1)
Отметим, что поскольку соответствующие частные производные в выражении (7.1) имеют положительные знаки, то при температурах выше абсолютного нуля СР>CV, а при температурах, близких к абсолютному нулю
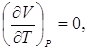
поэтому СР = СV , и так как при тех же температурах
![]()
то СР =СV=0.
Похожие работы
... сложным физическим понятием для учащихся. К этому понятию учащихся подводят на основе опытов по электризации тел. На основе опытов по электризации различных тел (стекла, эбонита, капрона, и т.д.) ищут ответ на следующие вопросы: 1. Только ли эбонит при натирании шерстью электризуется? 2. Обязательно ли натирать тела шерстью? 3. Электризуются оба или одно из натертых тел? 4. Зависит ли род заряда ...
... (молекулярно-кинетическая) и энергия взаимодействия молекул (молекулярно-потенциальная) являются частью внутренней энергии тела. Такой подход правомерен и с научной точки зрения, так как тепловые явления, изучаемые в школе, протекают в пределах среднего температурного диапазона, при котором изменение внутренней энергии тел связано главным образом с изменением кинетической и потенциальной энергии ...
... в другую. Процессы переноса теплоты представляют собой процессы обмена внутренней энергией между элементами рассматриваемой системы в форме теплоты. Общая характеристика и формулировка второго закона термодинамики Естественные процессы всегда направлены в сторону достижения системой равновесного состояния (механического, термического или любого другого). Это явление отражено вторым законом ...
... одного состояния в другое, получили название термодинамических потенциалов. Каждый из термодинамических потенциалов является однозначной функцией состояния системы. В термодинамике понятие термодинамического потенциала относят ко всей системе в целом (тогда как в физике обычно имеют дело с удельным потенциалом). Произведение называют иногда «связанной энергией». Это название станет понятным, ...
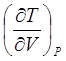
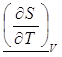
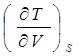
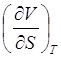
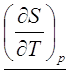
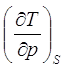
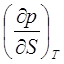
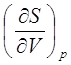



0 комментариев