Навигация
Определяют координаты точки максимума (минимума) функции и вычисляют значение целевой функции в этой точке
7. Определяют координаты точки максимума (минимума) функции и вычисляют значение целевой функции в этой точке.
Пример 1. Два больших войсковых соединения ![]() и
и ![]() к новому месту дислокации перевозятся по железной дороге. Для их погрузки выделяются три станции
к новому месту дислокации перевозятся по железной дороге. Для их погрузки выделяются три станции ![]() , с различными возможностями. Перевозка соединений осуществляется с соблюдением следующих ограничений:
, с различными возможностями. Перевозка соединений осуществляется с соблюдением следующих ограничений:
1. Количество перевозимых частей в соединении ![]() равно 6, а в
равно 6, а в ![]() –9.
–9.
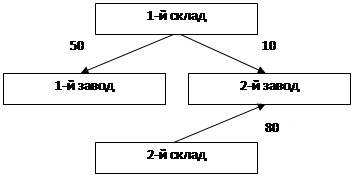
2. Каждая станция может принять определенное количество частей: ![]() .
.
3. На погрузку одной части станции затрачивают различное время (в сутках), которое указано в таблице.
| Соединения | Станция погрузки | ||
|
|
|
| |
|
| 3,0 4,5 | 4,0 6,5 | 2,5 3,5 |
Определить оптимальный вариант распределения частей по станциям погрузки, исходя из минимума суммарных затрат времени на погрузку.
Решение.
Решение штабов соединений состоит в распределении частей по станциям погрузки. Обозначим через ![]() число частей i-го соединения (i =1,2) на j-ой станции (j=1, 2, 3).
число частей i-го соединения (i =1,2) на j-ой станции (j=1, 2, 3).
Мы можем записать:
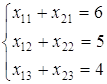
количество частей соединений на станциях погрузки ![]() соответственно.
соответственно.
![]() - количество частей соединения
- количество частей соединения ![]() на местах погрузки.
на местах погрузки.
![]() - количество частей соединения
- количество частей соединения ![]() на местах погрузки.
на местах погрузки.
![]()
Общая сумма затрат времени (в сутках) на погрузку есть
![]()
В этой задаче 6 переменных, но мы можем свести к двум.
Пусть ![]()
Тогда ![]()
Целевая функция имеет вид
![]()
Итак, надо найти ![]() при ограничениях:
при ограничениях:
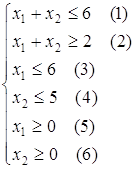
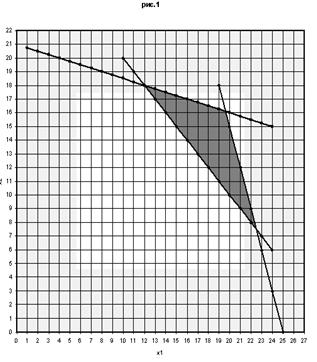
которая решается графически
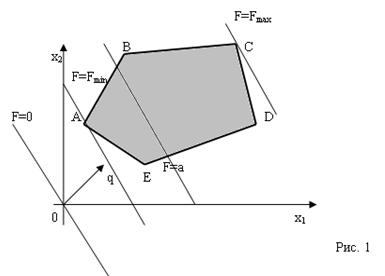
Возьмем прямую ![]() и начнем строить параллельные ей в направлении антиградиента, где
и начнем строить параллельные ей в направлении антиградиента, где ![]() .
.
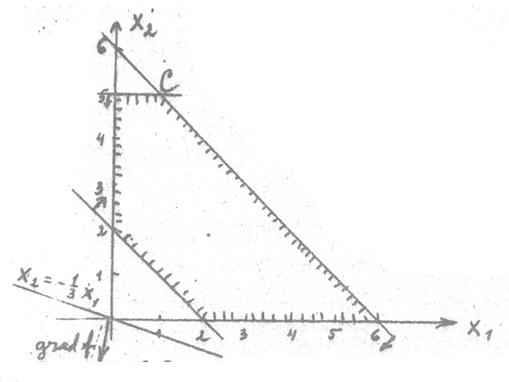
Последняя вершина многоугольника решений есть точка С, получаемая пересечением прямых (1) и (4). Решая, получим С (1;5).
Итак, оптимальные значения будут следующими: ![]() , а общие затраты времени
, а общие затраты времени ![]() (суток).
(суток).
§3 АНАЛИТИЧЕСКИЙ МЕТОД ОПТИМИЗАЦИИ
Пусть дана целевая функция ![]() .
.
Для нахождения наибольшего и наименьшего значения функции и (одной) вещественных переменных надо найти критические точки, в которых частные производные (производная) функции f по всем переменным обращается в 0. Кроме того, надо исследовать точки границы, если она принадлежит области определения. Среди них выбрать значения, где f принимает наибольшее и наименьшее значение.
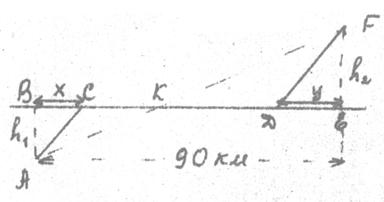 Пример 2. Определить оптимальный по времени маршрут выдвижения танкового подразделения из пункта А в пункт F, если допустимая скорость движения танков до дороги
Пример 2. Определить оптимальный по времени маршрут выдвижения танкового подразделения из пункта А в пункт F, если допустимая скорость движения танков до дороги ![]() , по дороге
, по дороге ![]() , за дорогой
, за дорогой ![]() . Удаление от дороге пункта А равно
. Удаление от дороге пункта А равно ![]() , пункта F
, пункта F ![]() . Расстояние между точками В и Е равно L = 90 км.
. Расстояние между точками В и Е равно L = 90 км.
Составим математическую модель, то есть найдем функцию цели. Нас интересует время. Время выдвижения из пункта А в пункт F.
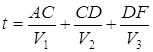
ВС = х км; DE = y км; АС = ![]()
CD = L – x – y; DF = ![]()
![]()
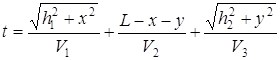
Составим функцию цели, которая зависит от двух переменных ![]()
Найдем критические точки
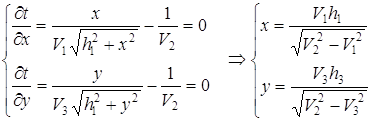
При данных условиях 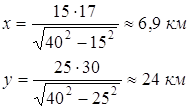
Найдем значение t при полученных x и y
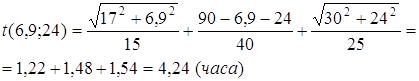
При вычислении значения t на границе, значения получаются больше, чем 4,24 часа. Следовательно, оптимальное решение будет при
х = 6,9 км, у = 24 км, ![]() .
.
![]()
Развитие современного общества характеризуется повышением технического уровня, усложнением организационной структуры производства, управления войсками, углублением общественного разделения труда, предъявлением высоких требований к методам планирования хозяйственного и военного руководства. В этих условиях только научный подход к руководству хозяйственной жизнью общества позволит обеспечить высокие темпы развития народного хозяйства. Научного подхода требует и решение тактических и стратегических задач, руководство военными операциями.
В настоящее время новейшие достижения математики и современной вычислительной техники находят все более широкое применение как в экономических исследованиях и планировании, так и в решении военных тактических задач. Этому способствует развитие таких разделов математики как математическое программирование, теория игр, теория массового обслуживания, а также бурное развитие быстродействующей электронно-вычислительной техники. Уже накоплен большой опыт постановки и решения экономических и тактических задач с помощью математических методов. Особенно успешно развиваются методы оптимального управления. Ярким примером применения современных математических методов является война Америки с Ираком и «Буря в пустыне». Там быстро развивается экономика и производство, где широко используются математические методы.
ЛИТЕРАТУРА
1. Тихонов А. Н., Костомаров Л. П. Вводные лекции по прикладной математике. М., Наука, 1984.
2. Кудрявцев Е. Н. Исследования операций в задачах, алгоритмах и программах. М., Наука, 1982.
3. Кузнецов Ю. Н., Кузубов В. И., Волощеноко А. В. Математическое программирование. М., Высшая школа, 1980.
4. Ильин В. А., Позняк Э. Г. Основы математического анализа. М., Наука, 1979.
Похожие работы
... часто представляются в виде алгоритма, в котором задаются математические соотношения, связывающие исходные данные и результат. В этом случае говорят о построении математической модели задачи. Обычно модель возникает как необходимый этап решения конкретной задачи. Однако в дельнейшем может происходить обособление модели от задачи, и модель начинает жить самостоятельно. Примером может служить сюжет ...
... предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации. Формулировка задачи линейного программирования Нужно максимизировать при условиях при i = 1, 2, 3, . . ., m.. Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от ...
... во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные. 2. Области применения и ограничения использования линейного программирования для решения экономических задач Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление ...
... является одним из быстро развивающихся направлений общей теории сложных систем. Многообразные методы исследования операций в настоящее время находят всё большее применение при проектировании, создании и эксплуатации автоматизированных систем управления, а также при решении сложных задач оптимизации технических и организационных систем. Вследствие этого необходимо изучать различные подходы при ...
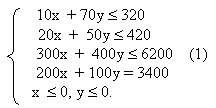
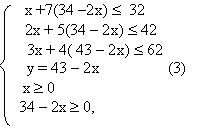
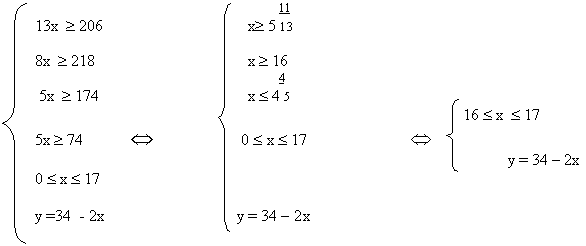

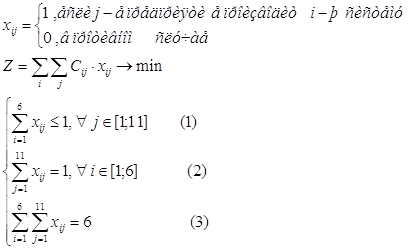
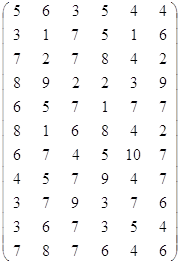

0 комментариев