Навигация
Министерство высшего и среднего специального образования Российской Федерации
Южноуральский Государственный Университет
Кафедра «цифровые радиотехнические системы»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКАК КУРСОВОМУ ПРОЕКТУ
по курсу:
ОСНОВЫ ТЕОРИИ ЦЕПЕЙЮУрГУ-К.200780.000 П3
Нормоконтролёр: РуководительКоровин В.М. Коровин В.М
«___»___________ 1999г. «___»___________ 1999г.
Автор проекта
Студент группы ПС-266
Суходоев Д.В.
«___»___________ 1999г.
Проект защищен с оценкой______________________
«___»___________ 1999г.
Челябинск
1999г.
Южноуральский Государственный Университет Факультет: ПСКафедра: ЦРТС
Заданиепо курсовой работе
студенту группы Суходоеву Дмитрию Владимировичу .
1) Тема работы: Анализ линейной динамической цепи .
2) Срок сдачи работы: _______________________________________
3) Исходные данные к работе: ________________________________
R = 1 кОм; Rн = 1 кОм; .
С1 = 1,5774·10-9 Ф; L1 = 0,6339·10-3 Гн; .
С2 = 2,3663·10-9 Ф; L1 = 0,4226·10-3 Гн; .
4) Содержание расчетно-пояснительной записки (перечень надлежащих разработке вопросов): 1) электрическая схема фильтра, система уравнений цепи; 2) комплексная функция передачи; 3) карта полюсов и нулей; 4) АЧХ, ФЧХ и импульсная характеристика .
5) Перечень графического материала: _________________________
________________________________________________________________________________________________________________
6) Консультанты по работе с указанием относящихся к ним разделов работы: _________________________________________
________________________________________________________________________________________________________________
7) Дата выдачи задания: _____________________________________
________________________________________________________
Руководитель: Коровин В.М. .
Задание принял к исполнению: ________________Подпись студента: ___________________________
АННОТАЦИЯ
Объем выполнения курсовой работы определен в учебном пособии [1].
Для выполнения работы был применен математический пакет MathCad v7.0 Pro © 1986-1997 by MathSoft, Inc, с его помощью было определено и построено: комплексная функция передачи цепи, карта полюсов и нулей, АЧХ, ФЧХ и импульсная характеристика.
СОДЕРЖАНИЕ
Введение……………………………………………………………..5
1. Электрическая схема фильтра
Система уравнений цепи………………………………………..…..6
2. Определение комплексной функции передачи…...…………….…8
3. Карта полюсов и нулей………………………………...………..…..9
4. Графики АЧХ и ФЧХ…………………………………………..…..11
5. Импульсная характеристика цепи……………………...…………13
Заключение…………………………………………………………14
Литература………………………………………………………….15
Приложение 1………………………………………………………16
Приложение 2………………………………………………………17
ВВЕДЕНИЕ
При выполнении курсовой работы необходимо отразить следующие
пункты: построить электрическую схему фильтра, составить систему уравнений цепи в обычной и матричной формах, определить комплексную функцию передачи цепи, перейти к операторной функции передачи и построить карту полюсов и нулей, также необходимо построить АЧХ, ФЧХ и импульсную характеристику, и в заключении курсового проекта необходимо отразить все аспекты выполнения тех или иных задач и написать список литературы, которой пользовались при выполнении работы.
1. ЭЛЕКТРИЧЕСКАЯ СХЕМА ФИЛЬТРА.
СИСТЕМА УРАВНЕНИЙ ЦЕПИ
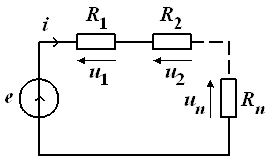
На рис.1 дана принципиальная электрическая схема фильтра, элементы данной схемы занесены в таблицу 1.
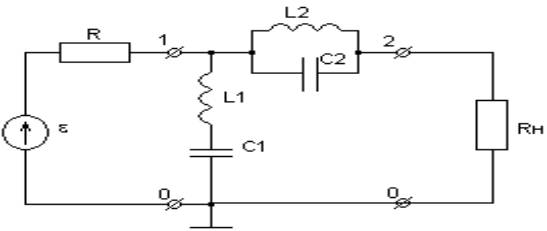
Рис.1 Электрическая схема фильтра.
Таблица 1.
| Наименование | Обозначение | Значение |
| Э.Д.С (источник) | e | - |
| Сопротивление | R | 1 кОм |
| Индуктивность | L1 | 0,6339·10-3 Гн |
| Конденсатор | С1 | 1,5774·10-9 Ф |
| Индуктивность | L2 | 0,4226·10-3 Гн |
| Конденсатор | С2 | 2,3663·10-9 Ф |
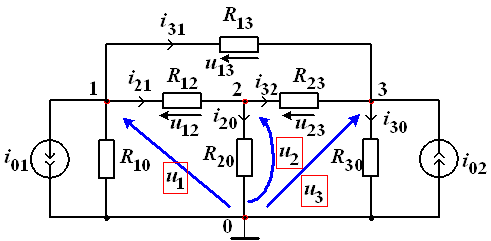
По имеющейся схеме составим систему уравнений цепи в обычной (скалярной) и матричной формах, применяя метод узловых напряжений. В качестве базисного узла взят узел «0»:
X1 = j(xL1-xC1); Y1 = 1/X1
© raVen design
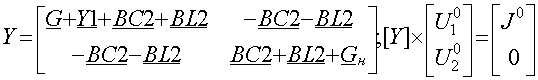
где:
G, Gн – активные проводимости;
Y, Y1, BC2, BL2, BC1, BL1 – реактивные комплексные проводимости;
U10, U20 – комплексные узловые напряжения соответствующих узлов;
J0 – комплексный ток задающего источника тока.
По матрице Y- проводимостей можно написать систему уравнений в скалярной форме:
U10(G + Y1 + BC2 + BL2) + U20( - BC2 – BL2) = J0
U20(BC2 + BL2 + Gн) + U10( - BC2 – BL2) = 0
Похожие работы
... можно строить схемы замещения реальных элементов цепи. 3. Топологические элементы схем Кроме рассмотренных элементов существуют топологические элементы, которые позволяют описать структуру цепи. Основные понятия: 1) Ветвь – соответствует участку цепи, в котором все элементы стоят последовательно, т.е. по которому протекает один и тот же ток. 2) Узел – место соединения трех и более ветвей ...
... любой из ветвей выбранного сечения приводит к связному графу. Отмеченные выше понятия и положения будут использованы в дальнейшем при расчете электрических цепей по методам, вытекающим из законов Кирхгофа. Теорема замещения В теории электрических цепей как при доказательствах ряда ее положений, так и при численных расчетах используется теорема замещения: значения всех напряжений и токов в ...
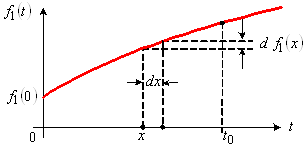
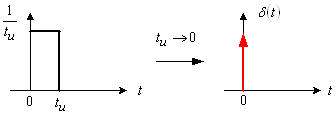
... соотношений и решает задачу вычисления реакции линейной электрической цепи на заданное непрерывное воздействие по известной переходной характеристики цепи . Эти соотношения называют интегралами Дюамеля. 3. Импульсные характеристики электрических цепей Импульсной характеристикой цепи называют отношение реакции цепи на импульсное воздействие к площади этого воздействия при нулевых начальных ...
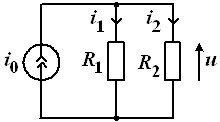
... Токи и находим по правилу деления тока : ; Напряжения на резисторах по известным токам в них вычисляются по закону Ома. Расчет резистивных электрических цепей методом токов ветвей Расчет сложных резистивных цепей, т. е. цепей, не сводящихся к последовательному или параллельному соединению элементов, основывается на использовании законов Кирхгофа. Если цепь имеет элементов, то ...




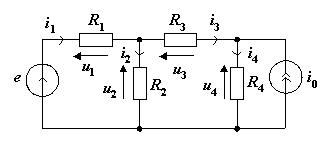



0 комментариев